第21章 21.4 第4课时 二次函数应用中的其他问题 课件(共16张PPT)
文档属性
| 名称 | 第21章 21.4 第4课时 二次函数应用中的其他问题 课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-16 21:36:10 | ||
图片预览






文档简介
(共16张PPT)
第4课时
二次函数应用中的其他问题
21.4
二次函数的应用
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
能为一些较简单的生活实际问题建立二次函数模型,并在此基础上,根据二次函数关系式和图象特点,从而解决实际问题.
【过程与方法】
经历探索问题的过程,获得利用数学方法解决实际问题的经验,感受数学模型和数学应用的价值,通过观察、比较、推理、交流等过程,发展获得一些研究问题与合作交流的方法与经验.
【情感态度】
通过动手实做及同学之间的合作与交流,让学生积累经验,发展学习动力.
【教学重点】
会根据不同的条件,利用二次函数解决生活中的实际问题.
【教学难点】
利用二次函数解决生活中的实际问题.
新课导入
行驶中的汽车,在制动后由于惯性,还要继续向前滑行一段距离才能停止,这段距离称为“制动距离”.为了了解某型号汽车的制动性能,对其进行了测试,测得数据如下表:
制动时车速/km·h-1
0
10
20
30
40
50
制动距离/m
0
0.3
1.0
2.1
3.6
5.5
有一辆该型号的汽车在公路上发生了交通事故,现场测得制动距离为46.5m,试问交通事故发生时车速是多少?是否因超速(该段公路限速110km/h)行驶导致了交通事故?
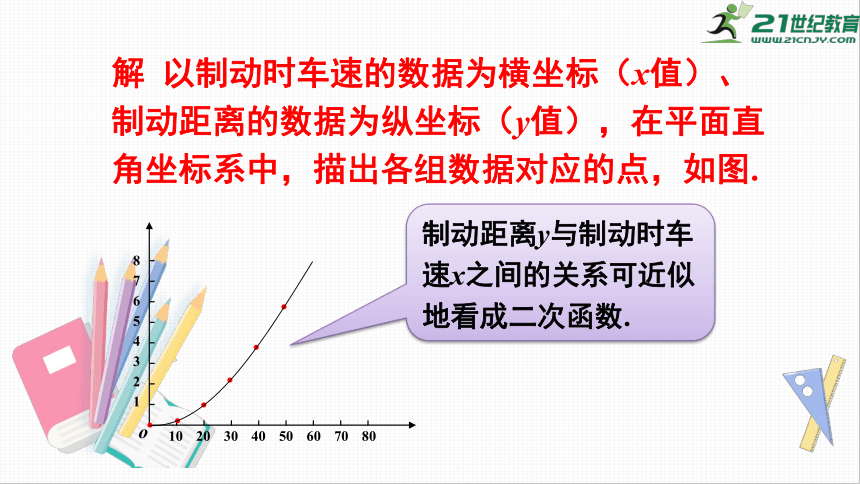
解
以制动时车速的数据为横坐标(x值)、制动距离的数据为纵坐标(y值),在平面直角坐标系中,描出各组数据对应的点,如图.
o
10
20
30
40
50
60
70
80
1
2
3
4
5
6
7
8
制动距离y与制动时车速x之间的关系可近似地看成二次函数.
设二次函数的表达式为y=ax2+bx+c在已知数据中任选三组,如取(0,0),(10,0.3),(20,1.0),分别代入所设函数的表达式,得
解方程组,得
所求函数的表达式为y=0.002x2+0.01x(x≥0)
把y=46.5m代入上式,得
46.5=0.002x2+0.01x.
解方程,得
x1=150(km/h),
x1=-155(km/h)(舍去)
答:制动时车速为150km/h(>110km/h),即在事故发生时,该汽车属超速行驶.
随堂练习
1.平时我们在跳绳时,绳甩到最高处的形状可近似地看为抛物线.如图所示,正在甩绳的甲、乙两名学生拿绳的手间距离为4m,距地面均为1m,学生丙、丁分别站在距甲拿绳的手水平距离1m、2.5m处.绳子在甩到最高处时刚好通过他们的头顶,已知学生丙的身高是1.5m,则学生丁的身高为________.
1.625m
2.如图,用长10m的铝合金条制成下部为矩形、上部为半圆的窗框(包括窗棱),若使此窗户的透光面积最大,则最大透光面积为(
)
A
B
D
C
C
3.羽毛球比赛中的某次运动路线可以看成是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(m)与水平距离x(m)之间满足关系
,则羽毛球飞行的最大高度为
(
)
A.1m
B.2m
C.3m
D.4m
B
4.如图,有一个抛物线形状的涵洞,其函数解析式为y=ax2(a≠0),涵洞跨度AB=12m,内部高度h=4m.为了安全,卡车经过涵洞时,载货(矩形)最高处与其正上方顶部之间的距离不能小于0.5m.现有一辆运货卡车欲通过涵洞,经测量,该车宽度为4m,载货最高处距地面2.5m.该车能否通过?为什么?
解:∵AB=12,内部高度h=4,∴A(-6,-4),代入y=ax2,得
-4=36a,∴a=
,∴
当x=2时,
∴
∴该车可以通过涵洞.
课堂小结
利用二次函数解决抛物线形问题的一般步骤:
(1)
建立适当的直角坐标系;
(2)
写出抛物线上的关键点的坐标;
(3)
运用待定系数法求出函数关系式;
(4)
求解数学问题;
(5)
求解抛物线形实际问题.
课后作业
1.完成课本课后习题;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第4课时
二次函数应用中的其他问题
21.4
二次函数的应用
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
能为一些较简单的生活实际问题建立二次函数模型,并在此基础上,根据二次函数关系式和图象特点,从而解决实际问题.
【过程与方法】
经历探索问题的过程,获得利用数学方法解决实际问题的经验,感受数学模型和数学应用的价值,通过观察、比较、推理、交流等过程,发展获得一些研究问题与合作交流的方法与经验.
【情感态度】
通过动手实做及同学之间的合作与交流,让学生积累经验,发展学习动力.
【教学重点】
会根据不同的条件,利用二次函数解决生活中的实际问题.
【教学难点】
利用二次函数解决生活中的实际问题.
新课导入
行驶中的汽车,在制动后由于惯性,还要继续向前滑行一段距离才能停止,这段距离称为“制动距离”.为了了解某型号汽车的制动性能,对其进行了测试,测得数据如下表:
制动时车速/km·h-1
0
10
20
30
40
50
制动距离/m
0
0.3
1.0
2.1
3.6
5.5
有一辆该型号的汽车在公路上发生了交通事故,现场测得制动距离为46.5m,试问交通事故发生时车速是多少?是否因超速(该段公路限速110km/h)行驶导致了交通事故?
解
以制动时车速的数据为横坐标(x值)、制动距离的数据为纵坐标(y值),在平面直角坐标系中,描出各组数据对应的点,如图.
o
10
20
30
40
50
60
70
80
1
2
3
4
5
6
7
8
制动距离y与制动时车速x之间的关系可近似地看成二次函数.
设二次函数的表达式为y=ax2+bx+c在已知数据中任选三组,如取(0,0),(10,0.3),(20,1.0),分别代入所设函数的表达式,得
解方程组,得
所求函数的表达式为y=0.002x2+0.01x(x≥0)
把y=46.5m代入上式,得
46.5=0.002x2+0.01x.
解方程,得
x1=150(km/h),
x1=-155(km/h)(舍去)
答:制动时车速为150km/h(>110km/h),即在事故发生时,该汽车属超速行驶.
随堂练习
1.平时我们在跳绳时,绳甩到最高处的形状可近似地看为抛物线.如图所示,正在甩绳的甲、乙两名学生拿绳的手间距离为4m,距地面均为1m,学生丙、丁分别站在距甲拿绳的手水平距离1m、2.5m处.绳子在甩到最高处时刚好通过他们的头顶,已知学生丙的身高是1.5m,则学生丁的身高为________.
1.625m
2.如图,用长10m的铝合金条制成下部为矩形、上部为半圆的窗框(包括窗棱),若使此窗户的透光面积最大,则最大透光面积为(
)
A
B
D
C
C
3.羽毛球比赛中的某次运动路线可以看成是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(m)与水平距离x(m)之间满足关系
,则羽毛球飞行的最大高度为
(
)
A.1m
B.2m
C.3m
D.4m
B
4.如图,有一个抛物线形状的涵洞,其函数解析式为y=ax2(a≠0),涵洞跨度AB=12m,内部高度h=4m.为了安全,卡车经过涵洞时,载货(矩形)最高处与其正上方顶部之间的距离不能小于0.5m.现有一辆运货卡车欲通过涵洞,经测量,该车宽度为4m,载货最高处距地面2.5m.该车能否通过?为什么?
解:∵AB=12,内部高度h=4,∴A(-6,-4),代入y=ax2,得
-4=36a,∴a=
,∴
当x=2时,
∴
∴该车可以通过涵洞.
课堂小结
利用二次函数解决抛物线形问题的一般步骤:
(1)
建立适当的直角坐标系;
(2)
写出抛物线上的关键点的坐标;
(3)
运用待定系数法求出函数关系式;
(4)
求解数学问题;
(5)
求解抛物线形实际问题.
课后作业
1.完成课本课后习题;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
