等腰三角形的性质说课PPT
文档属性
| 名称 | 等腰三角形的性质说课PPT |

|
|
| 格式 | rar | ||
| 文件大小 | 537.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-23 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
一、背景分析
1、学习任务分析
本节教材内容是在学生学习了三角形的有关知识,掌握了全等三角形的判定的基础上进行的。它不仅是对前面所学知识的运用,也是今后证明角相等、线段相等及两直线垂直的重要依据。而通过探究等腰三角形“三线合一”的性质,可以激发学生浓厚的学习数学的兴趣,使学生体会性质的来龙去脉。了解、感悟知识发生、发展的全过程,拓宽学生探索图形变化的视野。
本课的核心概念是:等腰三角形的定义。主要的数学思想:化归与转化。主要的数学方法:实验探究 感性认识 理性思考 严格的逻辑证明。本节课的重点是:等腰三角形的定义、性质定理及证明。
2、学生情况分析
学生前面学习了三角形的有关知识,会知道运用证明三角形的全等来证明线段、角的相等,这有利于证明等腰三形的性质。但对于证明过程中需要添加辅助线的情况遇到的比较少。
因此我把本节课的难点定为:等腰三角形中常用辅助线的作法。
二、教学目标设计
1、知识技能性目标:让学生通过实验猜想,主动探究的学习活动,发现并认同等腰三角形的性质定理及推论,探索归纳出它们的证明方法,并能应用其解决实际问题。
2、过程方法目标:让学生经历“设疑—探究—解决—收获”的学习过程,体会发现问题,探究问题的思想,从中感悟证明结论的方法和乐趣,初步了解作辅助线的技巧,培养“转化”及“化归”的数学思想方法。
3、情感价值观目标:在亲切、和谐、民主、活跃的探究氛围中,使学生产生浓厚的求知欲望和学习兴趣,使其个性得以充分张扬,帮助其培养成良好的学习习惯和勤于思考、勇于探索的思维品质。
4、解决问题:通过观察等腰三角形的对称性,培养学生观察、分析、归纳问题的能力。通过运用等腰三角形的性质解决有关的问题,提高运用知识和技能解决问题的能力,发展应用意识。
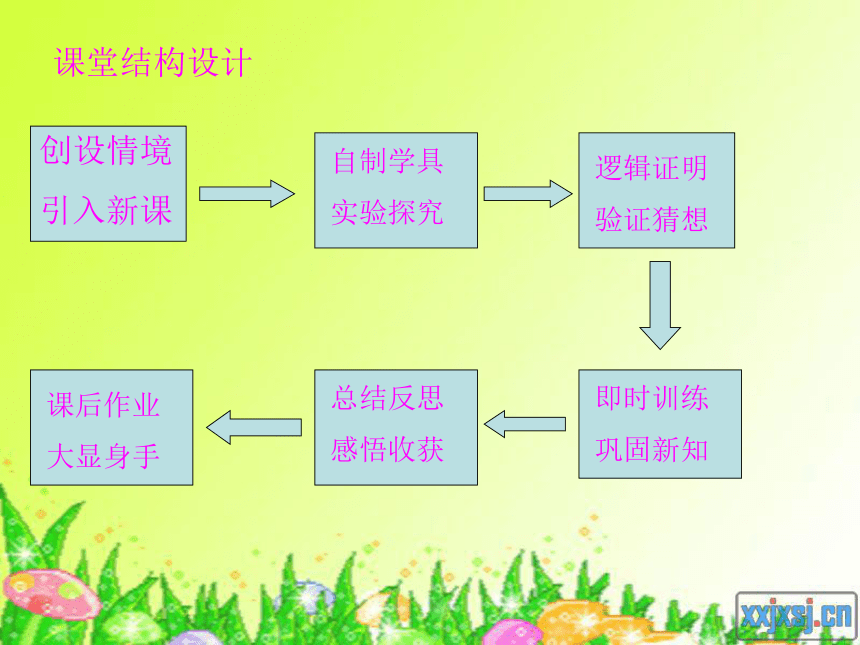
课堂结构设计
创设情境
引入新课
自制学具
实验探究
逻辑证明
验证猜想
即时训练
巩固新知
总结反思
感悟收获
课后作业
大显身手
四、教学媒体、设计
俗话说:学习要手到、口到、眼到、心到,这样才能把书念好。我班的学生活泼好动,且思维活跃,喜欢表达自己的见解,有一定的互动、互助基础。等腰三角形又是轴对称图形,需要利用轴对称来探究它的性质。所以我采用以下教学媒体进行教学。
1、教师教学媒体:多媒体课件,长方形纸、剪刀、三角板
2、学生准备:长方形纸、剪刀、三角板。
你从这些画面中看到了哪些几何图形?
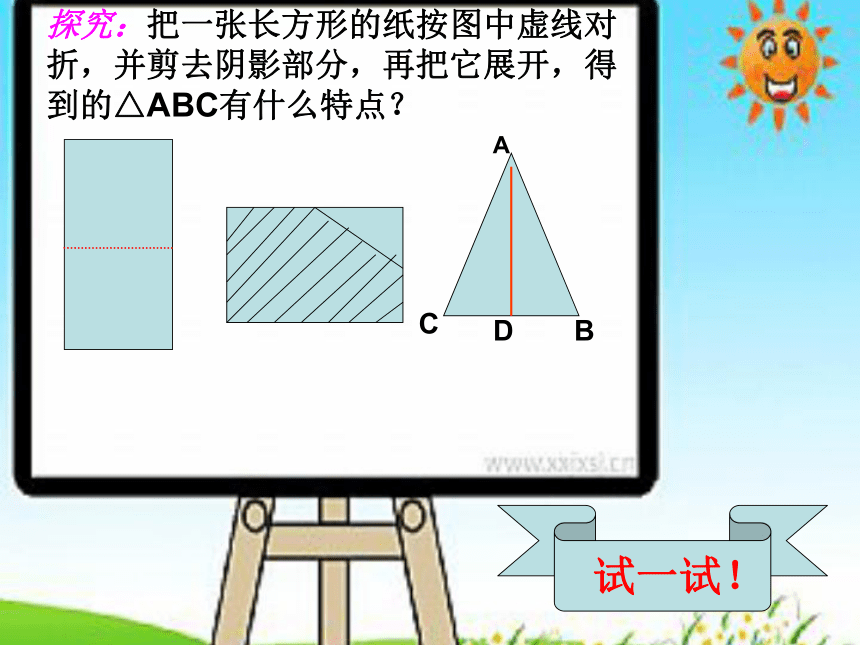
探究:把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点?
A
B
C
D
试一试!
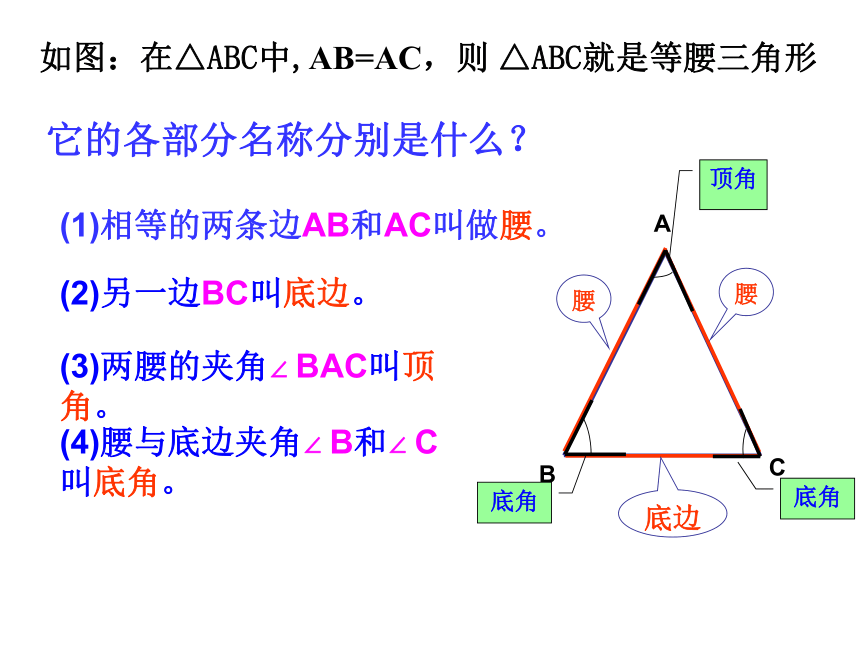
如图:在△ABC中,AB=AC,则 △ABC就是等腰三角形
它的各部分名称分别是什么?
A
B
C
(1)相等的两条边AB和AC叫做腰。
腰
腰
底边
(2)另一边BC叫底边。
顶角
底角
底角
(3)两腰的夹角∠ BAC叫顶角。
(4)腰与底边夹角∠ B和∠ C叫底角。
重合的线段
重合的角
AB与AC
BD与DC
AD与AD
∠B与∠C
∠BAD 与∠ CAD
∠ADB 与∠ADC
⑴上面剪出的等腰三角形是轴对称图形吗?
⑵把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角,填入下表
⑶由这些重合的线段和角,你能发现等腰三角形的性质吗?说一说你的猜想。
性质1 等腰三角形的两个底角 相等(简写成“等边对等角”)
性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合 (简称“三线合一”)
⑷交流实验结果总结等腰三角形性质
要注意是指顶角的平分线、底边上的高、底边上的中线这三线重合。
已知:△ABC中,AB=AC,求证:∠B=∠C
证明:作底边BC的中线AD
∵AB=AC,BD=CD,AD=AD
∴△ADB≌△ADC (SSS)
∴∠B=∠C
A
B
C
D
⑴性质1的条件和结论分别是什么?⑵用数学符号如何表达条件和结论?
试一试!
性质1的证明中辅助线的做法还有哪些?
⑴性质2的条件和结论分别是什么?
⑵用数学符号如何表述条件和结论?
⑴已知:△ABC中,AB=BC,AD是BC的中线
求证:AD⊥BC,AD平分∠BAC
⑵已知:△ABC中,AB=AC,AD是∠BAC的平分线
求证:AD⊥BC,AD是BC的中线
⑶已知△ABC中,AB=BC,AD⊥BC
求证:AD平分∠BAC,AD是BC的中线
A
B
C
D
试一试!
1、填空:如右图,在△ABC中,AB=AC
⑴∵AB=AC ∴∠ =∠
⑵∵AB=AC AD平分∠BAC
∴AD⊥ ,BD=———
⑶∵AB=AC, D⊥BC,
∴∠BAD=____,BD=______.
⑷∵AB=AC, AD是BC的中线.
∴AD⊥ ,∠BAD=____.
2、如果等腰三角形的顶角是36°,那么它的底角的度数是_______.
A
B
C
D
试一试!
3 例1:在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
解 ∵AB=AC,BD=BC=AD
∴∠ABC=∠C=∠BDC,∠A=∠ABD
设∠A=x 则
∠BDC=∠A+∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x
在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180°
解得x=36°
在△ABC中,∠A=36°,∠ABC=72°
A
B
C
D
(1)等腰三角形的一个角是36°,它的另外两个角是 。
(2)等腰三角形的一个角是100°,它的另外两个角是 。
要注意分类讨论哦!
(3)如图,在下列等腰三角形中,分别求出它们的底角的度数
°
(4)如图△ABC是等腰直角三角形(AB=AC,∠BAC=90°),AD是底边BC上的高,标出∠B、∠C、∠BAD、∠DAC的度数。图中有哪些相等的线段?
(5)如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数。
46
0
120
0
A
C
B
D
A
B
C
D
等腰三角形
1、等边对等角(性质定理)
(等腰三角形的两底角相等)
2、三线合一
(等腰三角形顶角平分线、底边上的中线、底边上的高互相重合)
3 、等腰三角形中常用辅助线的添加方法
作业:
1、基础作业(必做):①56 页第1题;②57页第8题;③预习第51-53页。
2、探究作业(选做):等腰三角形两个外角之比为1:4,你能得出它顶角的度数吗?
六、评价设计
1、对学生参与探究过程的积极性进行 评价,促进学生养成动手操作,用脑思考的习惯。
2、对学生与同学合作交流的意识进行评价,培养学生合作探究的意识。
3、对不同层次的学生采取分层次的评价方式,培养学生对数学的学习兴趣。
七、板书设计
12.3.1等腰三角形
1、有两条边相等的三角形叫等腰三角形,相等的两条边叫腰,另一边叫底边,两腰所夹的角叫顶角,底边与腰的夹角叫底角。
2、等腰三角形的性质
性质1 等腰三角形的两个底角相等(简写成“等边对等角”)
性质2 等腰三角形的顶角平分线,底边上的中线,底边上的高相互重合
一、背景分析
1、学习任务分析
本节教材内容是在学生学习了三角形的有关知识,掌握了全等三角形的判定的基础上进行的。它不仅是对前面所学知识的运用,也是今后证明角相等、线段相等及两直线垂直的重要依据。而通过探究等腰三角形“三线合一”的性质,可以激发学生浓厚的学习数学的兴趣,使学生体会性质的来龙去脉。了解、感悟知识发生、发展的全过程,拓宽学生探索图形变化的视野。
本课的核心概念是:等腰三角形的定义。主要的数学思想:化归与转化。主要的数学方法:实验探究 感性认识 理性思考 严格的逻辑证明。本节课的重点是:等腰三角形的定义、性质定理及证明。
2、学生情况分析
学生前面学习了三角形的有关知识,会知道运用证明三角形的全等来证明线段、角的相等,这有利于证明等腰三形的性质。但对于证明过程中需要添加辅助线的情况遇到的比较少。
因此我把本节课的难点定为:等腰三角形中常用辅助线的作法。
二、教学目标设计
1、知识技能性目标:让学生通过实验猜想,主动探究的学习活动,发现并认同等腰三角形的性质定理及推论,探索归纳出它们的证明方法,并能应用其解决实际问题。
2、过程方法目标:让学生经历“设疑—探究—解决—收获”的学习过程,体会发现问题,探究问题的思想,从中感悟证明结论的方法和乐趣,初步了解作辅助线的技巧,培养“转化”及“化归”的数学思想方法。
3、情感价值观目标:在亲切、和谐、民主、活跃的探究氛围中,使学生产生浓厚的求知欲望和学习兴趣,使其个性得以充分张扬,帮助其培养成良好的学习习惯和勤于思考、勇于探索的思维品质。
4、解决问题:通过观察等腰三角形的对称性,培养学生观察、分析、归纳问题的能力。通过运用等腰三角形的性质解决有关的问题,提高运用知识和技能解决问题的能力,发展应用意识。
课堂结构设计
创设情境
引入新课
自制学具
实验探究
逻辑证明
验证猜想
即时训练
巩固新知
总结反思
感悟收获
课后作业
大显身手
四、教学媒体、设计
俗话说:学习要手到、口到、眼到、心到,这样才能把书念好。我班的学生活泼好动,且思维活跃,喜欢表达自己的见解,有一定的互动、互助基础。等腰三角形又是轴对称图形,需要利用轴对称来探究它的性质。所以我采用以下教学媒体进行教学。
1、教师教学媒体:多媒体课件,长方形纸、剪刀、三角板
2、学生准备:长方形纸、剪刀、三角板。
你从这些画面中看到了哪些几何图形?
探究:把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点?
A
B
C
D
试一试!
如图:在△ABC中,AB=AC,则 △ABC就是等腰三角形
它的各部分名称分别是什么?
A
B
C
(1)相等的两条边AB和AC叫做腰。
腰
腰
底边
(2)另一边BC叫底边。
顶角
底角
底角
(3)两腰的夹角∠ BAC叫顶角。
(4)腰与底边夹角∠ B和∠ C叫底角。
重合的线段
重合的角
AB与AC
BD与DC
AD与AD
∠B与∠C
∠BAD 与∠ CAD
∠ADB 与∠ADC
⑴上面剪出的等腰三角形是轴对称图形吗?
⑵把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角,填入下表
⑶由这些重合的线段和角,你能发现等腰三角形的性质吗?说一说你的猜想。
性质1 等腰三角形的两个底角 相等(简写成“等边对等角”)
性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合 (简称“三线合一”)
⑷交流实验结果总结等腰三角形性质
要注意是指顶角的平分线、底边上的高、底边上的中线这三线重合。
已知:△ABC中,AB=AC,求证:∠B=∠C
证明:作底边BC的中线AD
∵AB=AC,BD=CD,AD=AD
∴△ADB≌△ADC (SSS)
∴∠B=∠C
A
B
C
D
⑴性质1的条件和结论分别是什么?⑵用数学符号如何表达条件和结论?
试一试!
性质1的证明中辅助线的做法还有哪些?
⑴性质2的条件和结论分别是什么?
⑵用数学符号如何表述条件和结论?
⑴已知:△ABC中,AB=BC,AD是BC的中线
求证:AD⊥BC,AD平分∠BAC
⑵已知:△ABC中,AB=AC,AD是∠BAC的平分线
求证:AD⊥BC,AD是BC的中线
⑶已知△ABC中,AB=BC,AD⊥BC
求证:AD平分∠BAC,AD是BC的中线
A
B
C
D
试一试!
1、填空:如右图,在△ABC中,AB=AC
⑴∵AB=AC ∴∠ =∠
⑵∵AB=AC AD平分∠BAC
∴AD⊥ ,BD=———
⑶∵AB=AC, D⊥BC,
∴∠BAD=____,BD=______.
⑷∵AB=AC, AD是BC的中线.
∴AD⊥ ,∠BAD=____.
2、如果等腰三角形的顶角是36°,那么它的底角的度数是_______.
A
B
C
D
试一试!
3 例1:在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
解 ∵AB=AC,BD=BC=AD
∴∠ABC=∠C=∠BDC,∠A=∠ABD
设∠A=x 则
∠BDC=∠A+∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x
在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180°
解得x=36°
在△ABC中,∠A=36°,∠ABC=72°
A
B
C
D
(1)等腰三角形的一个角是36°,它的另外两个角是 。
(2)等腰三角形的一个角是100°,它的另外两个角是 。
要注意分类讨论哦!
(3)如图,在下列等腰三角形中,分别求出它们的底角的度数
°
(4)如图△ABC是等腰直角三角形(AB=AC,∠BAC=90°),AD是底边BC上的高,标出∠B、∠C、∠BAD、∠DAC的度数。图中有哪些相等的线段?
(5)如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数。
46
0
120
0
A
C
B
D
A
B
C
D
等腰三角形
1、等边对等角(性质定理)
(等腰三角形的两底角相等)
2、三线合一
(等腰三角形顶角平分线、底边上的中线、底边上的高互相重合)
3 、等腰三角形中常用辅助线的添加方法
作业:
1、基础作业(必做):①56 页第1题;②57页第8题;③预习第51-53页。
2、探究作业(选做):等腰三角形两个外角之比为1:4,你能得出它顶角的度数吗?
六、评价设计
1、对学生参与探究过程的积极性进行 评价,促进学生养成动手操作,用脑思考的习惯。
2、对学生与同学合作交流的意识进行评价,培养学生合作探究的意识。
3、对不同层次的学生采取分层次的评价方式,培养学生对数学的学习兴趣。
七、板书设计
12.3.1等腰三角形
1、有两条边相等的三角形叫等腰三角形,相等的两条边叫腰,另一边叫底边,两腰所夹的角叫顶角,底边与腰的夹角叫底角。
2、等腰三角形的性质
性质1 等腰三角形的两个底角相等(简写成“等边对等角”)
性质2 等腰三角形的顶角平分线,底边上的中线,底边上的高相互重合
