1.5　成轴对称图形的性质（第1课时）

1.5　成轴对称图形的性质（第1课时）
一、教与学目标：
1、经历探索轴对称图形的性质的过程，理解连接对应点的线段被对成轴平分、对应线段相等、对应角相等的性质。
2、会用成轴对称的图形的性质解决相应问题。
二、教与学重点难点：
成轴对称的图形的性质及其应用。
三、教与学方法：
通过动手操作让学生经历探索轴对称图形的性质的过程，激发学习与应用数学知识的兴趣
四、教与学过程：
（一）、情境导入：
如图：把一张对折后扎一个孔，然后展开铺平。连接得到的两个小孔A和A/ ，线段AA′与折痕MN交点为O，线段AA′与直线MN的位置关系？
你还发现了什么关系？
（二）、探究新知：
利用扎纸孔的方法，探索成轴对称的图形的性质。
通过扎空，我们可得到如下结论：
两个点关于某一直线成轴对称，
那么连接这两点的线段被
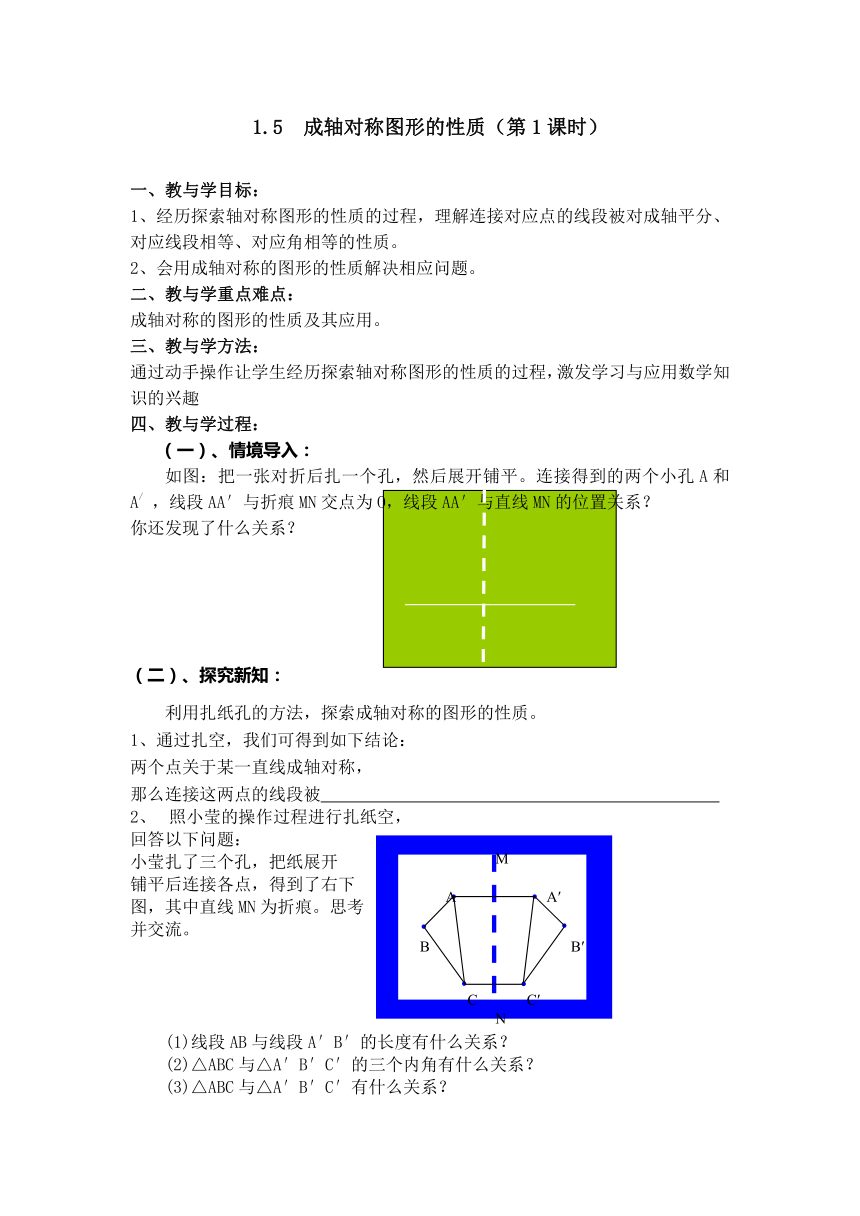
照小莹的操作过程进行扎纸空，
回答以下问题：
小莹扎了三个孔，把纸展开
铺平后连接各点，得到了右下
图，其中直线MN为折痕。思考
并交流。
(1)线段AB与线段A′B′的长度有什么关系？
(2)△ABC与△A′B′C′的三个内角有什么关系？
(3)△ABC与△A′B′C′有什么关系？
个性化设计：
由此我们得到成轴对称的图形的性质是：
精讲点拨：
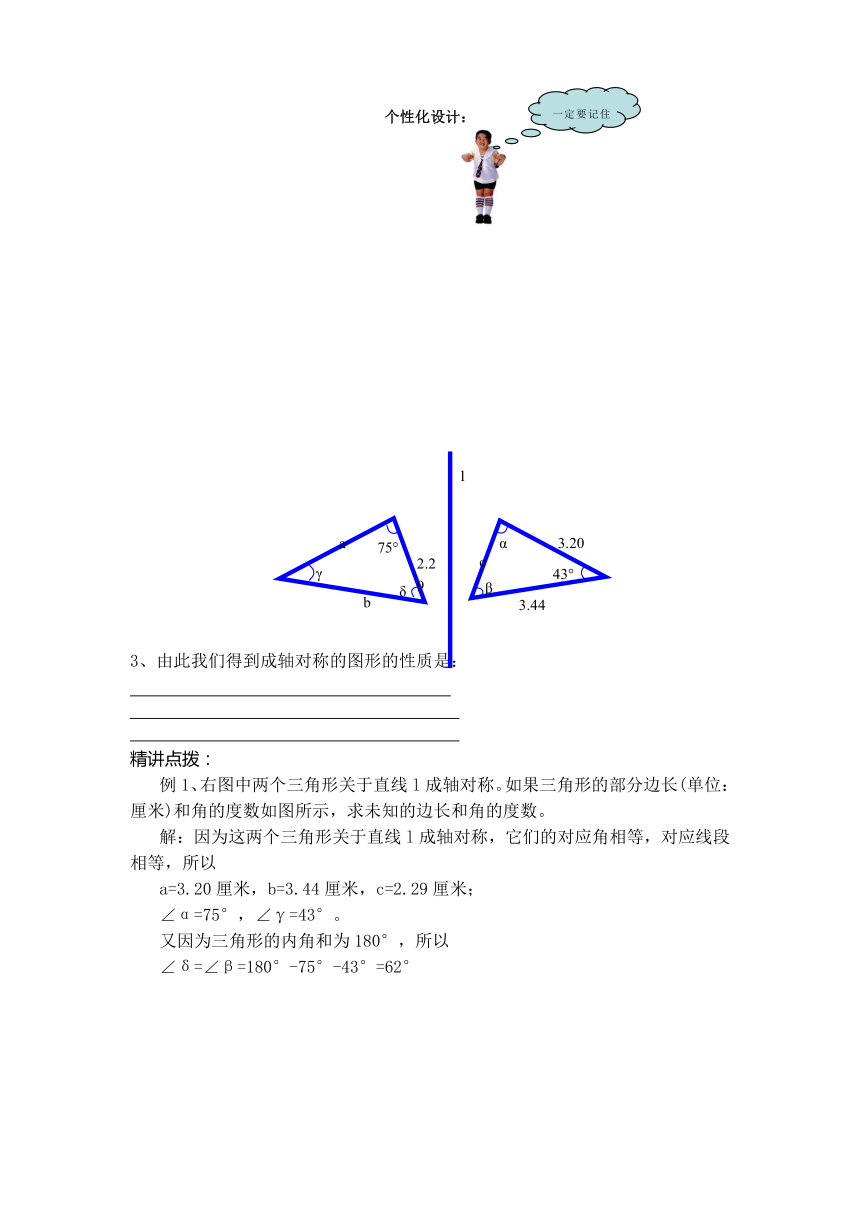
例1、右图中两个三角形关于直线l成轴对称。如果三角形的部分边长(单位：厘米)和角的度数如图所示，求未知的边长和角的度数。
解：因为这两个三角形关于直线l成轴对称，它们的对应角相等，对应线段相等，所以
a=3.20厘米，b=3.44厘米，c=2.29厘米；
∠α=75°，∠γ=43°。
又因为三角形的内角和为180°，所以
∠δ=∠β=180°-75°-43°=62°
学以致用：
1、巩固新知：
（1）． 已知△ABC关于直线MN的轴对称图形△A‘B’C‘，分别连结对应点AA’、BB’、CC’交对称轴于D、E、F.找出与下列相等的量。
AD＝ ， BF＝ ，CE＝ .
∠ADM＝ ，∠BFN＝ ， ∠CEN＝ 。
（2）完成如下习题
个性化设计
达标测评：
1、成轴对称的两个图形，对应点所连的线段被对称轴_______． 对应线段_______，对应角_______．
2、 如果点M,N关于直线成轴对称，那么线段MN与直线的关系是_____被__ _垂直平分．
3、已知四边形ABCD，及它关于x轴的对称四边形A′B′C′D′（如图）
写出图中相等的线段：
五、课堂小结：
本节课我们学习的是正数和负数的定义以及有理数的分类。
作业布置：
关于x轴的对称的图形对应点的坐标有什么特点？
习题1.5A组T1
七、教学反思：
个性化设计：
A
A′
B
B′
C
C′
M
N
一定要记住哟!
l
75°
γ
a
b
δ
2.29
3.20
3.44
c
β
43°
α