2020-2021学年北京版小学六年级数学上册《第6章 扇形统计图》单元测试题(含解析)
文档属性
| 名称 | 2020-2021学年北京版小学六年级数学上册《第6章 扇形统计图》单元测试题(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-13 21:54:29 | ||
图片预览



文档简介
2020-2021学年北京版小学六年级数学上册《第6章
扇形统计图》单元测试题
一、单选题(共8题)
1.要表示各种农作物种植数量与总种植数量的关系,应选择(??
)统计图比较合适。
A.?条形?????????????????????????????????????????B.?扇形?????????????????????????????????????????C.?折线
2.哪种统计图可以表示各部分数量与总数之间的关系.(????
)
A.?条形统计图
???????????????????????????????B.?扇形统计图???????????????????????????????C.?折线统计图
3.圆形花坛内种花情况如右图。可以用(???
)条形统计图表示各种花占地面积的关系。
A.???????????????????B.???????????????????C.???????????????????D.?
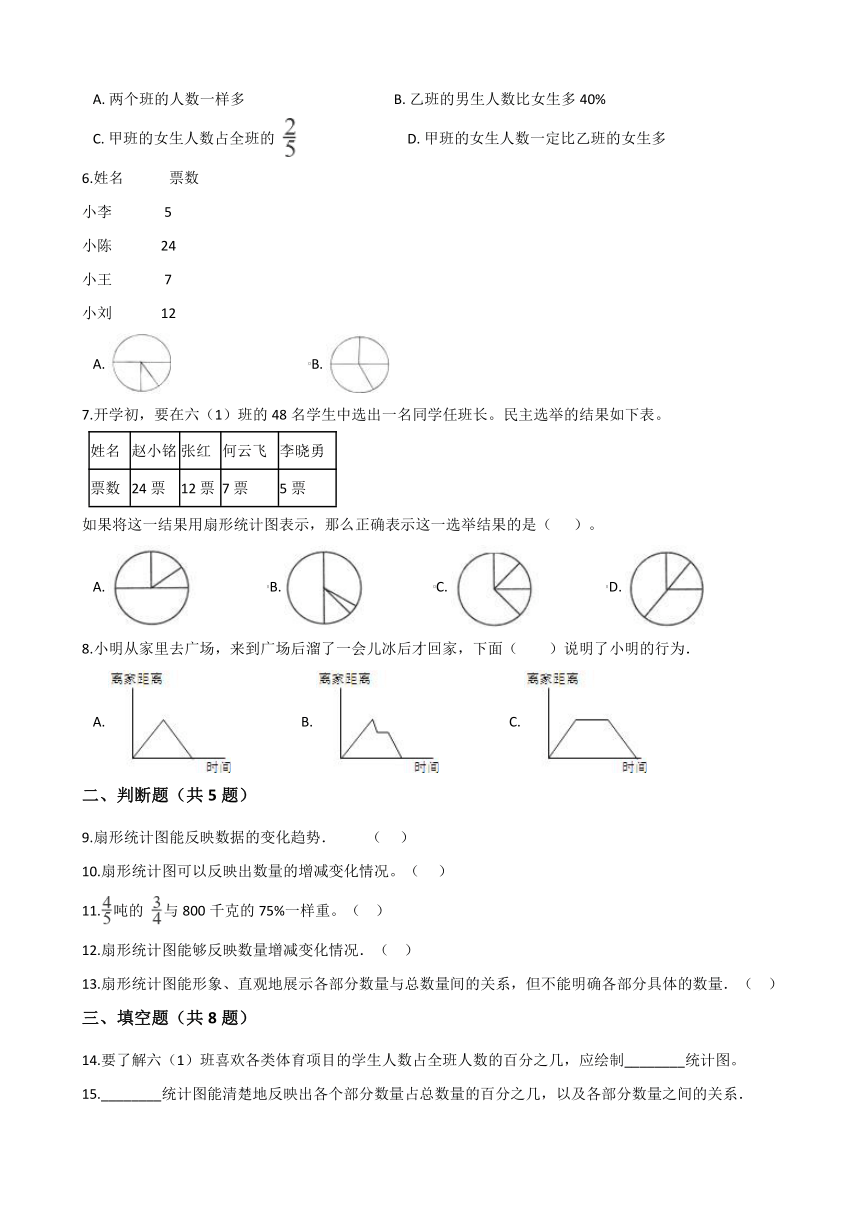
4.右边条形图是从曙光中学800名学生中帮助四川地震失学儿童捐款?
金额的部分抽样调查数据,扇形图是该校各年级人数比例分布图.那么该校七年级同学捐款的总数大约为(?
)
A.?870元??????????????????????????????B.?4200元??????????????????????????????C.?5010元??????????????????????????????D.?250560元
5.下面是甲、乙两个班男、女生人数分布统计图,其中说法正确的是(
??),
A.?两个班的人数一样多???????????????????????????????????????????B.?乙班的男生人数比女生多40%
C.?甲班的女生人数占全班的
???????????????????????????????D.?甲班的女生人数一定比乙班的女生多
6.姓名???????????
票数
小李?????????????
5
小陈????????????
24
小王?????????????
7
小刘????????????
12
A.?????????????????????????????????????????B.?
7.开学初,要在六(1)班的48名学生中选出一名同学任班长。民主选举的结果如下表。
姓名
赵小铭
张红
何云飞
李晓勇
票数
24票
12票
7票
5票
如果将这一结果用扇形统计图表示,那么正确表示这一选举结果的是(????
)。
A.????????????????????B.?????????????????????C.????????????????????D.?
8.小明从家里去广场,来到广场后溜了一会儿冰后才回家,下面( )说明了小明的行为.
A.?????????????????????B.?????????????????????C.?
二、判断题(共5题)
9.扇形统计图能反映数据的变化趋势.
(???
)
10.扇形统计图可以反映出数量的增减变化情况。(???
)
11.吨的
与800千克的75%一样重。(??
)
12.扇形统计图能够反映数量增减变化情况.(
??)
13.扇形统计图能形象、直观地展示各部分数量与总数量间的关系,但不能明确各部分具体的数量.(??
)
三、填空题(共8题)
14.要了解六(1)班喜欢各类体育项目的学生人数占全班人数的百分之几,应绘制________统计图。
15.________统计图能清楚地反映出各个部分数量占总数量的百分之几,以及各部分数量之间的关系.
16.________统计图可以直观地表示出数量的多少;________统计图不但可以表示出数量的多少,还可以反映数量的增减变化情况;________统计图可以清楚地表示出各部分数量与总数量之间的关系。
17.扇形统计图很清楚的表示出________与________之间的关系.
18.六年级组有775人,男生占六年级组的52%,男生有________人。
19.校图书室周一~周五日借书量的统计,要求注重数据,宜采用________。
20.在
、2.67、2.06%、26.7%中最大是________,最小的是________;2米的
与________的20%一样长.
21.下图是空气中成分的统计图。如果人类每呼吸一次需要纯氧气63毫升。那么在呼吸时至少呼入空气________?毫升。
四、解答题(共7题)
22.仔细观察,把统计图表补充完整。
某小学4-6年级男生近视人数统计表
年级
男生近视人数/人
四年级
40
五年级
60
六年级
23.根据平均气温统计图完成下面的统计表,并回答问题.
(1)根据统计图完成下表.(年平均气温保留整数)
(2)两地平均气温最核近的是________季度,平均气温差距最大的是________季度.
(3)一年中,________市的平均气温比较高,________市的平均气温变化较大.
24.下面某小学二年级各班人数统计图。
(1)二年5班学生人数占二年级总人数的百分之几?
(2)如果二年1班有学生42人,那么二年级一共有多少学生?
25.某超市“2019年成交金额约26亿元,比2018年增长约30%”,2018年这个超市的成交金额约是多少?
26.如下图,已知农场的经济作物比粮食作物少10.4公顷。这个农场其它作物有多少公顷?
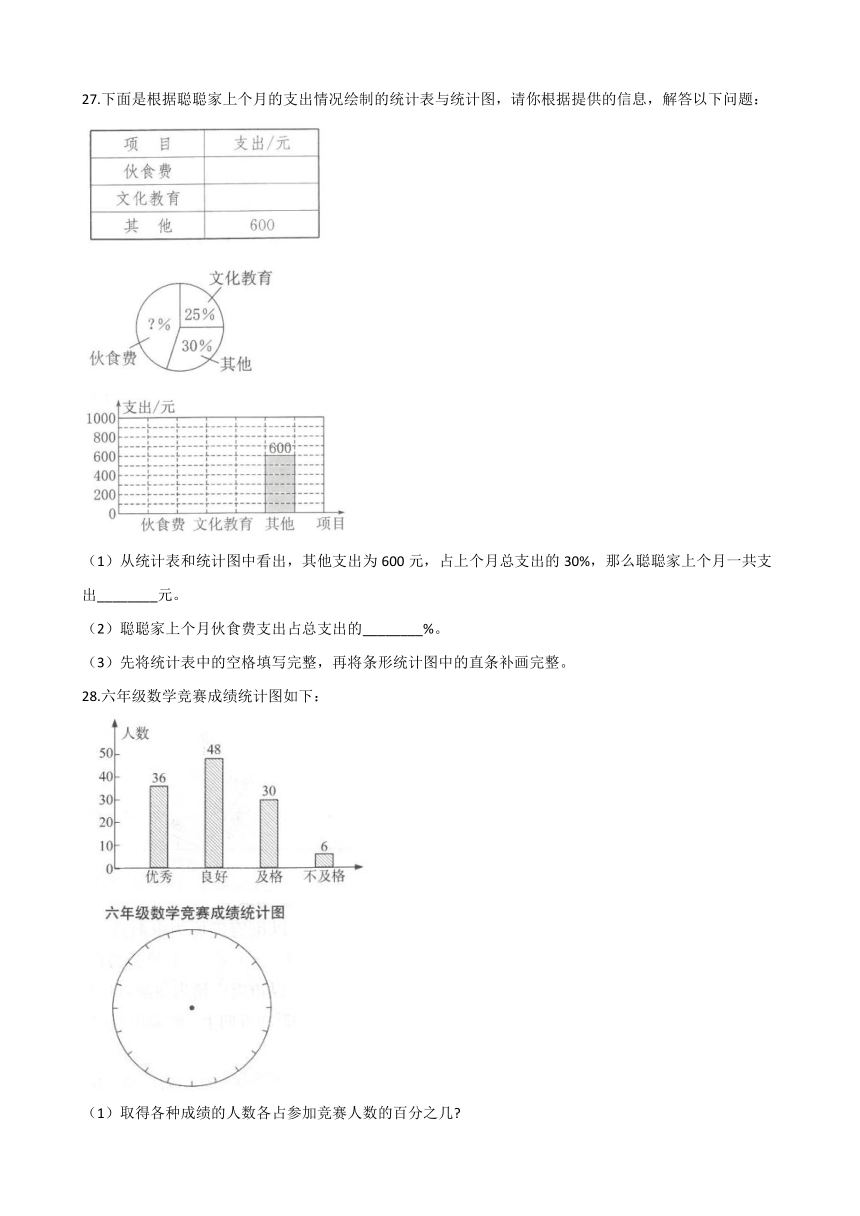
27.下面是根据聪聪家上个月的支出情况绘制的统计表与统计图,请你根据提供的信息,解答以下问题:
(1)从统计表和统计图中看出,其他支出为600元,占上个月总支出的30%,那么聪聪家上个月一共支出________元。
(2)聪聪家上个月伙食费支出占总支出的________%。
(3)先将统计表中的空格填写完整,再将条形统计图中的直条补画完整。
28.六年级数学竞赛成绩统计图如下:
(1)取得各种成绩的人数各占参加竞赛人数的百分之几?
(2)请根据上面的条形统计图完成扇形统计图。
答案解析部分
一、单选题
1.【答案】
B
【解析】【解答】要表示各种农作物种植数量与总种植数量的关系,应选择扇形统计图比较合适.
故答案为:B.
【分析】根据三种统计图的作用可知,条形统计图中很容易看出各种数量的多少;折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况;扇形统计图可以很清楚地表示各部分数量同总数之间的关系,据此选择即可.
2.【答案】
B
【解析】【解答】解:扇形统计图表示各部分与数量与总数之间的关系。
故答案为:B。
【分析】扇形统计图用整圆表示总数,用扇形表示各部分数量,表示各部分数字占总数的关系。
3.【答案】
C
【解析】【解答】解:A:兰花和菊花的直条长度不相等,错误;
B:兰花和菊花的直条长度太短,错误;
C:兰花和菊花的直条长度相等且它们的和等于玫瑰花的直条长度,正确;
D:兰花和菊花的直条长度太长,错误;
故答案为:C。
【分析】从扇形统计图上可以看出,玫瑰花的种植面积等于兰花和菊花的种植面积之和,且兰花和菊花的种植面积相等,所以条形统计图中,兰花和菊花的直条长度要一样,且它们的和等于玫瑰花的长度。
4.【答案】
C
【解析】【解答】解:800×36%=288(人);
4+8+10+16+12=50(人);
4÷50=
;
8÷50=
;
10÷50=
;
16÷50=
;
12÷50=
;
288×
×5,
=23.04×5,
=115.2(元);
288×
×10,
=46.8×10,
=468(元);
288×
×15,
=57.6×15,
=864(元);
288×
×20,
=92.16×20,
=1843.2(元);
288×
×25,
=69.12×25,
=1728(元);
115.2+468+864+1843.2+1728,
=583.2+864+1843.2+1728,
=1447.2+1843.2+1728,
=3290.2+1728,
=5018.2,
≈5010(元).
故答案选:C.
【分析】先由扇形统计图读出年级的七人数占总人数的百分之几,再用总人数乘这个百分数求出七年级的总人数;
再由条形统计图捐5元,10元,15元,20元,25元的各有多少人,进而求出它们各占抽样总人数的百分之几;再用七年级的总人数乘这些分率,求出捐5元,10元,15元,20元,25元大约各有多少人,最后用人数乘它们对应捐的钱数然后再加起来即可.本题是根据给出的部分数量来推算全部的数量;关键是要根据统计图读数所需要的数量,特别是由这些数量来求部分人数求出部分占总人数的几分之几.
5.【答案】
C
【解析】【解答】40%=0.4=
故答案为:C
【分析】首先,没有信息能确定两个班人数一样多。其次,乙班男生与女生相差40%是相差总人数的40%。再次,两个班人数不定,不能确定甲班女生人数一定比乙班女生多。因此,甲班女生40%是把甲班人数看做单位“1”。
6.【答案】
A
【解析】【解答】解:5+24+7+12=48(票);小李:360°×=37.5°,小陈:360°×=180°,小王:360°×52.5°,小刘:360°×=90°.A图中有圆心角是180°的扇形.
故答案为:A
【分析】先计算出总票数,然后分别求出每人得的票数占总票数的几分之几,然后计算出所在扇形的圆心角的度数,根据圆心角的度数确定哪个图形可以表示票数与总票数之间的关系即可.
7.【答案】
A
【解析】【解答】解:赵小铭:24÷48=50%,即赵小铭的票数是全班同学的50%,即占圆的一半;
张红:12÷48=25%,张红的票数是全班同学的25%,即占圆的;
何云飞和李晓勇共占全班人数的25%,即占圆的;
综合可得选项A符合题意。
故答案为:A。
【分析】扇形统计图是用整个圆表示总数(单位"1"),用圆内过圆心O点的各个扇形的大小表示各部分量占总量的百分之几,扇形统计图中各部分的百分比之和是单位"1"。本题中分别计算出赵小铭、张红的票数占全班同学的百分之多少,即可得出答案。
8.【答案】C
【解析】【解答】解:“小明从家里去广场”用图来表示应是小明离家的距离逐渐变远,“来到广场后溜了一会儿冰”此时的距离是固定的,“再回家”距离变近.
所以C符合题意.
故选:C.
【分析】由于“小明从家里去广场,来到广场后溜了一会儿冰后才回家”用图来表示应是小明离家的距离逐渐变远,然后“在广场后溜了一会儿冰”时的距离固定,再回家变近;据此解答.
二、判断题
9.【答案】错误
【解析】【解答】扇形统计图:能很清楚地表示出各部分数量同总数的关系,不能反映数据的变化趋势,故原题说法错误.
故答案为:错误.
【分析】根据统计图的特点可知,条形统计图:能很容易看出各种数量的多少;折线统计图:不但能表示数量的多少,还能表示出数量增减变化;扇形统计图:能很清楚地表示出各部分数量同总数的关系.
10.【答案】
错误
【解析】【解答】扇形统计图可以看出部分占总体的多少,折线统计图可以看出数量的增减变化情况。
故答案为:错误。
【分析】根据扇形统计图的特点进行判断即可。
11.【答案】
正确
【解析】【解答】解:=0.6(吨)
800×75%=600(吨)
他们一样重
故答案为:正确。
【分析】求一个数的几分之几(或百分之几)是多少用乘法;本题先计算,再比较是不是一样重。
12.【答案】
错误
【解析】【解答】解:扇形统计图能表示部分与整体之间的关系。原题说法错误。
故答案为:错误。
【分析】扇形统计图能表示部分与整体之间的关系,折线统计图才能反映数量的增减变化情况。
13.【答案】
正确
【解析】【解答】
扇形统计图能形象、直观地展示各部分数量与总数量间的关系,但不能明确各部分具体的数量,此题说法正确.
故答案为:正确.
【分析】此题主要考查了统计图的特征,条形统计图特点:可以清楚地看出数量的多少;折线统计图特点:不但可以表示数量的多少,还可以清楚的看出数量的增减变化情况;扇形统计图特点:可以看出各个部分数量与总数之间的关系,据此判断.
三、填空题
14.【答案】
扇形
【解析】【解答】解:要了解六(1)班喜欢各类体育项目的学生人数占全班人数的百分之几,应绘制扇形统计图。
故答案为:扇形。
【分析】扇形统计图是用整个圆表示总数,用圆内过圆心O点的各个扇形的大小表示各部分量占总量的百分之几。通过扇形统计图可以很清楚地表示出各部分数量与总数之间的关系。
15.【答案】
扇形
【解析】【解答】根据统计图的特点可知,扇形统计图能清楚地反映出各个部分数量占总数量
百分之几,以及各部分数量之间的关系.
故答案为:扇形
【分析】条形统计图能清楚地表示出数量的多少;折线统计图不仅能表示出数量的多少,还能表示出数量的增减变化情况;扇形统计图能表示出部分与整体之间的关系.
16.【答案】
条形;折线;扇形
【解析】【解答】条形统计图可以直观地表示出数量的多少;
折线统计图不但可以表示出数量的多少,还可以反映数量的增减变化情况;
扇形统计图可以清楚地表示出各部分数量与总数量之间的关系。
故答案为:条形;折线;扇形.
【分析】常见的统计图有三种:条形统计图、折线统计图、扇形统计图,根据这三种统计图的特点解答.
17.【答案】各部分;整体
【解析】根据扇形统计图的知识:扇形统计图能更直观、清楚地反映各部分与总体的关系
18.【答案】403
【解析】【解答】解:男生有775×52%=403人。
故答案为:403。【分析】男生的人数=六年级组的总人数×男生占六年级组的百分之几。
19.【答案】统计表
【解析】【解答】统计表更着重于数据本身。
【分析】根据简单的统计表、统计图的选择,即得某校图书室周一~周五日借书量的统计,要求注重数据,宜采用统计表。
20.【答案】
2.67;2.06%;4
【解析】【解答】解:(1)
=2.6,2.06%=0.0206,26.7%=0.267,因此,2.67>2.6>0.267>0.0206,即2.67>
>26.7%>2.06%,最大的是2.67,最小的是2.06%.(2)2×
=
(米)
÷20%=4(米)即2米的
与4的20%一样长.
故答案为:2.67,2.06%,4.
【分析】(1)把分数、百分数都化成保留一定位数的小数,再根据小数的大小比较方法进行比较,即可确定哪个数最大,哪个数最小.(2)根据分数乘法的意义2米的
是2×
=
米,再根据百分数除法的意义,用
米除以20%就是与2米的
与一样长米数.此题考查的知识有小数与分数的互化、小数的大小比较、分数乘、除法的意义及应用等.
21.【答案】300
【解析】63÷21%=300毫升。
四、解答题
22.【答案】
某小学4-6年级男生近视人数统计表
年级
男生近视人数/人
四年级
40
五年级
60
六年级
100
【解析】【解答】60÷30%=200(人)
四年级:40÷200=20%,
六年级:1-20%-30%
=80%-30%
=50%
六年级:200×50%=100(人)。
【分析】根据统计图可知,五年级男生近视人数占三个年级男生近视总人数的30%,根据统计表可知,五年级男生近视人数有60人,五年级男生近视人数÷五年级男生近视人数占三个年级男生近视总人数的百分比=三个年级男生近视的总人数;
再用四年级的男生近视人数÷总人数=四年级男生近视人数占三个年级男生近视总人数的百分比;
把三个年级男生近视总人数看作单位“1”,单位“1”-四年级男生近视人数占三个年级男生近视总人数的百分比-五年级男生近视人数占三个年级男生近视总人数的百分比=六年级男生近视人数占三个年级男生近视总人数的百分比,据此列式解答;
要求六年级男生近视的人数,用三个年级男生近视的总人数×六年级男生近视人数占三个年级男生近视总人数的百分比=六年级男生近视人数,据此计算补充统计图和统计表。
23.【答案】
(1)解:观察图例,可知白色直条表示北京市气温,涂色直条表示桂林市气温;
(1+20+24+6)÷4
=51÷4
≈13(℃)
(12+23+28+16)÷4
=79÷4
≈20(℃)
统计表如下:
(2)第二;第一
(3)桂林;北京
【解析】【分析】(1)根据统计图中的数据作答即可,其中年平均气温=四个季度的平均气温之和÷4;
(2)将每个季度的两地的平均气温作差,差最小的,那么这个季度两地平均气温最接近,差最大的,那么这个季度两地平均气温最接近;
(3)把每个季度每个城市的平均气温进行比较即可。
24.【答案】
(1)解:1-(19%+22%+19%+21%)
=1-81%
=19%
答:
二年5班学生人数占二年级总人数的19%。
(2)解:
42÷21%=200(人)
答:
二年级一共有200人。
【解析】【分析】(1)根据扇形统计图可知,把二年级的总人数看作单位“1”,单位“1”-二年级1~4班一共占总人数的百分比=二年级5班学生人数占总人数的百分比,据此列式解答;
(2)已知二年级1班人数与二年级1班占总人数的百分比,可以求出二年级的总人数,二年级1班人数÷二年级1班占总人数的百分比=二年级的总人数,据此列式解答。
25.【答案】
解:26÷(1+30%)
=26÷1.3
=20(亿元)
答:2018年这个超市的成交金额约是20亿元。
【解析】【分析】以2018年的成交金额为单位“1”,2019年的是2018年的(1+30%),根据分数除法的意义计算即可。
26.【答案】
解:10.4÷(60%-34%)×6%=2.4(公顷)
答:这个农场其它作物有2.4公顷。
【解析】【分析】此题主要考查了百分数的应用,根据统计图可知,粮食作物占60%,经济作物占34%,其他作物占6%,农场的经济作物比粮食作物少的质量÷农场的经济作物比粮食作物少占总量的百分比=这个农场所有作物的总质量,然后用这个农场所有作物的总质量×其他作物占总量的百分比=其他作物的质量,据此列式解答。
27.【答案】
(1)2000
(2)45
(3)伙食费900,文化教育500,表格略
补画的条形统计图如图
【解析】【解答】解:(1)一共支出:600÷30%=2000(元);
(2)1-25%-30%=45%;
(3)文化教育:2000×25%=400(元);伙食费:2000×45%=900(元),
统计表如下:
故答案为:(1)2000;(2)45。
【分析】(1)根据分数除法的意义,用其他支出的钱数除以占总支出的百分率即可求出一共支出的钱数;
(2)用1减去文化教育占的百分率和其他占的百分率即可求出伙食费支出所占的百分率;
(3)用总支出乘伙食费占的百分率求出伙食费支出数,再求出文化教育支出数,再填表;根据计算出的数据结合统计图中的数据绘制出条形统计图即可。
28.【答案】
(1)解:参加竞赛人数:36+48+30+6=120(人)
×100%=30%
×100%=40%
×100%=25%
×100%=5%
(2)
【解析】【分析】(1)根据统计图中的数据用加法计算出总人数,用优秀、良好、及格、不及格的人数分别除以总人数,分别求出各部分人数占总人数的百分率;
(2)扇形统计图中平均分成20格,每格就是5%,根据各部分占的百分率确定扇形的大小,然后画出统计图即可。
扇形统计图》单元测试题
一、单选题(共8题)
1.要表示各种农作物种植数量与总种植数量的关系,应选择(??
)统计图比较合适。
A.?条形?????????????????????????????????????????B.?扇形?????????????????????????????????????????C.?折线
2.哪种统计图可以表示各部分数量与总数之间的关系.(????
)
A.?条形统计图
???????????????????????????????B.?扇形统计图???????????????????????????????C.?折线统计图
3.圆形花坛内种花情况如右图。可以用(???
)条形统计图表示各种花占地面积的关系。
A.???????????????????B.???????????????????C.???????????????????D.?
4.右边条形图是从曙光中学800名学生中帮助四川地震失学儿童捐款?
金额的部分抽样调查数据,扇形图是该校各年级人数比例分布图.那么该校七年级同学捐款的总数大约为(?
)
A.?870元??????????????????????????????B.?4200元??????????????????????????????C.?5010元??????????????????????????????D.?250560元
5.下面是甲、乙两个班男、女生人数分布统计图,其中说法正确的是(
??),
A.?两个班的人数一样多???????????????????????????????????????????B.?乙班的男生人数比女生多40%
C.?甲班的女生人数占全班的
???????????????????????????????D.?甲班的女生人数一定比乙班的女生多
6.姓名???????????
票数
小李?????????????
5
小陈????????????
24
小王?????????????
7
小刘????????????
12
A.?????????????????????????????????????????B.?
7.开学初,要在六(1)班的48名学生中选出一名同学任班长。民主选举的结果如下表。
姓名
赵小铭
张红
何云飞
李晓勇
票数
24票
12票
7票
5票
如果将这一结果用扇形统计图表示,那么正确表示这一选举结果的是(????
)。
A.????????????????????B.?????????????????????C.????????????????????D.?
8.小明从家里去广场,来到广场后溜了一会儿冰后才回家,下面( )说明了小明的行为.
A.?????????????????????B.?????????????????????C.?
二、判断题(共5题)
9.扇形统计图能反映数据的变化趋势.
(???
)
10.扇形统计图可以反映出数量的增减变化情况。(???
)
11.吨的
与800千克的75%一样重。(??
)
12.扇形统计图能够反映数量增减变化情况.(
??)
13.扇形统计图能形象、直观地展示各部分数量与总数量间的关系,但不能明确各部分具体的数量.(??
)
三、填空题(共8题)
14.要了解六(1)班喜欢各类体育项目的学生人数占全班人数的百分之几,应绘制________统计图。
15.________统计图能清楚地反映出各个部分数量占总数量的百分之几,以及各部分数量之间的关系.
16.________统计图可以直观地表示出数量的多少;________统计图不但可以表示出数量的多少,还可以反映数量的增减变化情况;________统计图可以清楚地表示出各部分数量与总数量之间的关系。
17.扇形统计图很清楚的表示出________与________之间的关系.
18.六年级组有775人,男生占六年级组的52%,男生有________人。
19.校图书室周一~周五日借书量的统计,要求注重数据,宜采用________。
20.在
、2.67、2.06%、26.7%中最大是________,最小的是________;2米的
与________的20%一样长.
21.下图是空气中成分的统计图。如果人类每呼吸一次需要纯氧气63毫升。那么在呼吸时至少呼入空气________?毫升。
四、解答题(共7题)
22.仔细观察,把统计图表补充完整。
某小学4-6年级男生近视人数统计表
年级
男生近视人数/人
四年级
40
五年级
60
六年级
23.根据平均气温统计图完成下面的统计表,并回答问题.
(1)根据统计图完成下表.(年平均气温保留整数)
(2)两地平均气温最核近的是________季度,平均气温差距最大的是________季度.
(3)一年中,________市的平均气温比较高,________市的平均气温变化较大.
24.下面某小学二年级各班人数统计图。
(1)二年5班学生人数占二年级总人数的百分之几?
(2)如果二年1班有学生42人,那么二年级一共有多少学生?
25.某超市“2019年成交金额约26亿元,比2018年增长约30%”,2018年这个超市的成交金额约是多少?
26.如下图,已知农场的经济作物比粮食作物少10.4公顷。这个农场其它作物有多少公顷?
27.下面是根据聪聪家上个月的支出情况绘制的统计表与统计图,请你根据提供的信息,解答以下问题:
(1)从统计表和统计图中看出,其他支出为600元,占上个月总支出的30%,那么聪聪家上个月一共支出________元。
(2)聪聪家上个月伙食费支出占总支出的________%。
(3)先将统计表中的空格填写完整,再将条形统计图中的直条补画完整。
28.六年级数学竞赛成绩统计图如下:
(1)取得各种成绩的人数各占参加竞赛人数的百分之几?
(2)请根据上面的条形统计图完成扇形统计图。
答案解析部分
一、单选题
1.【答案】
B
【解析】【解答】要表示各种农作物种植数量与总种植数量的关系,应选择扇形统计图比较合适.
故答案为:B.
【分析】根据三种统计图的作用可知,条形统计图中很容易看出各种数量的多少;折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况;扇形统计图可以很清楚地表示各部分数量同总数之间的关系,据此选择即可.
2.【答案】
B
【解析】【解答】解:扇形统计图表示各部分与数量与总数之间的关系。
故答案为:B。
【分析】扇形统计图用整圆表示总数,用扇形表示各部分数量,表示各部分数字占总数的关系。
3.【答案】
C
【解析】【解答】解:A:兰花和菊花的直条长度不相等,错误;
B:兰花和菊花的直条长度太短,错误;
C:兰花和菊花的直条长度相等且它们的和等于玫瑰花的直条长度,正确;
D:兰花和菊花的直条长度太长,错误;
故答案为:C。
【分析】从扇形统计图上可以看出,玫瑰花的种植面积等于兰花和菊花的种植面积之和,且兰花和菊花的种植面积相等,所以条形统计图中,兰花和菊花的直条长度要一样,且它们的和等于玫瑰花的长度。
4.【答案】
C
【解析】【解答】解:800×36%=288(人);
4+8+10+16+12=50(人);
4÷50=
;
8÷50=
;
10÷50=
;
16÷50=
;
12÷50=
;
288×
×5,
=23.04×5,
=115.2(元);
288×
×10,
=46.8×10,
=468(元);
288×
×15,
=57.6×15,
=864(元);
288×
×20,
=92.16×20,
=1843.2(元);
288×
×25,
=69.12×25,
=1728(元);
115.2+468+864+1843.2+1728,
=583.2+864+1843.2+1728,
=1447.2+1843.2+1728,
=3290.2+1728,
=5018.2,
≈5010(元).
故答案选:C.
【分析】先由扇形统计图读出年级的七人数占总人数的百分之几,再用总人数乘这个百分数求出七年级的总人数;
再由条形统计图捐5元,10元,15元,20元,25元的各有多少人,进而求出它们各占抽样总人数的百分之几;再用七年级的总人数乘这些分率,求出捐5元,10元,15元,20元,25元大约各有多少人,最后用人数乘它们对应捐的钱数然后再加起来即可.本题是根据给出的部分数量来推算全部的数量;关键是要根据统计图读数所需要的数量,特别是由这些数量来求部分人数求出部分占总人数的几分之几.
5.【答案】
C
【解析】【解答】40%=0.4=
故答案为:C
【分析】首先,没有信息能确定两个班人数一样多。其次,乙班男生与女生相差40%是相差总人数的40%。再次,两个班人数不定,不能确定甲班女生人数一定比乙班女生多。因此,甲班女生40%是把甲班人数看做单位“1”。
6.【答案】
A
【解析】【解答】解:5+24+7+12=48(票);小李:360°×=37.5°,小陈:360°×=180°,小王:360°×52.5°,小刘:360°×=90°.A图中有圆心角是180°的扇形.
故答案为:A
【分析】先计算出总票数,然后分别求出每人得的票数占总票数的几分之几,然后计算出所在扇形的圆心角的度数,根据圆心角的度数确定哪个图形可以表示票数与总票数之间的关系即可.
7.【答案】
A
【解析】【解答】解:赵小铭:24÷48=50%,即赵小铭的票数是全班同学的50%,即占圆的一半;
张红:12÷48=25%,张红的票数是全班同学的25%,即占圆的;
何云飞和李晓勇共占全班人数的25%,即占圆的;
综合可得选项A符合题意。
故答案为:A。
【分析】扇形统计图是用整个圆表示总数(单位"1"),用圆内过圆心O点的各个扇形的大小表示各部分量占总量的百分之几,扇形统计图中各部分的百分比之和是单位"1"。本题中分别计算出赵小铭、张红的票数占全班同学的百分之多少,即可得出答案。
8.【答案】C
【解析】【解答】解:“小明从家里去广场”用图来表示应是小明离家的距离逐渐变远,“来到广场后溜了一会儿冰”此时的距离是固定的,“再回家”距离变近.
所以C符合题意.
故选:C.
【分析】由于“小明从家里去广场,来到广场后溜了一会儿冰后才回家”用图来表示应是小明离家的距离逐渐变远,然后“在广场后溜了一会儿冰”时的距离固定,再回家变近;据此解答.
二、判断题
9.【答案】错误
【解析】【解答】扇形统计图:能很清楚地表示出各部分数量同总数的关系,不能反映数据的变化趋势,故原题说法错误.
故答案为:错误.
【分析】根据统计图的特点可知,条形统计图:能很容易看出各种数量的多少;折线统计图:不但能表示数量的多少,还能表示出数量增减变化;扇形统计图:能很清楚地表示出各部分数量同总数的关系.
10.【答案】
错误
【解析】【解答】扇形统计图可以看出部分占总体的多少,折线统计图可以看出数量的增减变化情况。
故答案为:错误。
【分析】根据扇形统计图的特点进行判断即可。
11.【答案】
正确
【解析】【解答】解:=0.6(吨)
800×75%=600(吨)
他们一样重
故答案为:正确。
【分析】求一个数的几分之几(或百分之几)是多少用乘法;本题先计算,再比较是不是一样重。
12.【答案】
错误
【解析】【解答】解:扇形统计图能表示部分与整体之间的关系。原题说法错误。
故答案为:错误。
【分析】扇形统计图能表示部分与整体之间的关系,折线统计图才能反映数量的增减变化情况。
13.【答案】
正确
【解析】【解答】
扇形统计图能形象、直观地展示各部分数量与总数量间的关系,但不能明确各部分具体的数量,此题说法正确.
故答案为:正确.
【分析】此题主要考查了统计图的特征,条形统计图特点:可以清楚地看出数量的多少;折线统计图特点:不但可以表示数量的多少,还可以清楚的看出数量的增减变化情况;扇形统计图特点:可以看出各个部分数量与总数之间的关系,据此判断.
三、填空题
14.【答案】
扇形
【解析】【解答】解:要了解六(1)班喜欢各类体育项目的学生人数占全班人数的百分之几,应绘制扇形统计图。
故答案为:扇形。
【分析】扇形统计图是用整个圆表示总数,用圆内过圆心O点的各个扇形的大小表示各部分量占总量的百分之几。通过扇形统计图可以很清楚地表示出各部分数量与总数之间的关系。
15.【答案】
扇形
【解析】【解答】根据统计图的特点可知,扇形统计图能清楚地反映出各个部分数量占总数量
百分之几,以及各部分数量之间的关系.
故答案为:扇形
【分析】条形统计图能清楚地表示出数量的多少;折线统计图不仅能表示出数量的多少,还能表示出数量的增减变化情况;扇形统计图能表示出部分与整体之间的关系.
16.【答案】
条形;折线;扇形
【解析】【解答】条形统计图可以直观地表示出数量的多少;
折线统计图不但可以表示出数量的多少,还可以反映数量的增减变化情况;
扇形统计图可以清楚地表示出各部分数量与总数量之间的关系。
故答案为:条形;折线;扇形.
【分析】常见的统计图有三种:条形统计图、折线统计图、扇形统计图,根据这三种统计图的特点解答.
17.【答案】各部分;整体
【解析】根据扇形统计图的知识:扇形统计图能更直观、清楚地反映各部分与总体的关系
18.【答案】403
【解析】【解答】解:男生有775×52%=403人。
故答案为:403。【分析】男生的人数=六年级组的总人数×男生占六年级组的百分之几。
19.【答案】统计表
【解析】【解答】统计表更着重于数据本身。
【分析】根据简单的统计表、统计图的选择,即得某校图书室周一~周五日借书量的统计,要求注重数据,宜采用统计表。
20.【答案】
2.67;2.06%;4
【解析】【解答】解:(1)
=2.6,2.06%=0.0206,26.7%=0.267,因此,2.67>2.6>0.267>0.0206,即2.67>
>26.7%>2.06%,最大的是2.67,最小的是2.06%.(2)2×
=
(米)
÷20%=4(米)即2米的
与4的20%一样长.
故答案为:2.67,2.06%,4.
【分析】(1)把分数、百分数都化成保留一定位数的小数,再根据小数的大小比较方法进行比较,即可确定哪个数最大,哪个数最小.(2)根据分数乘法的意义2米的
是2×
=
米,再根据百分数除法的意义,用
米除以20%就是与2米的
与一样长米数.此题考查的知识有小数与分数的互化、小数的大小比较、分数乘、除法的意义及应用等.
21.【答案】300
【解析】63÷21%=300毫升。
四、解答题
22.【答案】
某小学4-6年级男生近视人数统计表
年级
男生近视人数/人
四年级
40
五年级
60
六年级
100
【解析】【解答】60÷30%=200(人)
四年级:40÷200=20%,
六年级:1-20%-30%
=80%-30%
=50%
六年级:200×50%=100(人)。
【分析】根据统计图可知,五年级男生近视人数占三个年级男生近视总人数的30%,根据统计表可知,五年级男生近视人数有60人,五年级男生近视人数÷五年级男生近视人数占三个年级男生近视总人数的百分比=三个年级男生近视的总人数;
再用四年级的男生近视人数÷总人数=四年级男生近视人数占三个年级男生近视总人数的百分比;
把三个年级男生近视总人数看作单位“1”,单位“1”-四年级男生近视人数占三个年级男生近视总人数的百分比-五年级男生近视人数占三个年级男生近视总人数的百分比=六年级男生近视人数占三个年级男生近视总人数的百分比,据此列式解答;
要求六年级男生近视的人数,用三个年级男生近视的总人数×六年级男生近视人数占三个年级男生近视总人数的百分比=六年级男生近视人数,据此计算补充统计图和统计表。
23.【答案】
(1)解:观察图例,可知白色直条表示北京市气温,涂色直条表示桂林市气温;
(1+20+24+6)÷4
=51÷4
≈13(℃)
(12+23+28+16)÷4
=79÷4
≈20(℃)
统计表如下:
(2)第二;第一
(3)桂林;北京
【解析】【分析】(1)根据统计图中的数据作答即可,其中年平均气温=四个季度的平均气温之和÷4;
(2)将每个季度的两地的平均气温作差,差最小的,那么这个季度两地平均气温最接近,差最大的,那么这个季度两地平均气温最接近;
(3)把每个季度每个城市的平均气温进行比较即可。
24.【答案】
(1)解:1-(19%+22%+19%+21%)
=1-81%
=19%
答:
二年5班学生人数占二年级总人数的19%。
(2)解:
42÷21%=200(人)
答:
二年级一共有200人。
【解析】【分析】(1)根据扇形统计图可知,把二年级的总人数看作单位“1”,单位“1”-二年级1~4班一共占总人数的百分比=二年级5班学生人数占总人数的百分比,据此列式解答;
(2)已知二年级1班人数与二年级1班占总人数的百分比,可以求出二年级的总人数,二年级1班人数÷二年级1班占总人数的百分比=二年级的总人数,据此列式解答。
25.【答案】
解:26÷(1+30%)
=26÷1.3
=20(亿元)
答:2018年这个超市的成交金额约是20亿元。
【解析】【分析】以2018年的成交金额为单位“1”,2019年的是2018年的(1+30%),根据分数除法的意义计算即可。
26.【答案】
解:10.4÷(60%-34%)×6%=2.4(公顷)
答:这个农场其它作物有2.4公顷。
【解析】【分析】此题主要考查了百分数的应用,根据统计图可知,粮食作物占60%,经济作物占34%,其他作物占6%,农场的经济作物比粮食作物少的质量÷农场的经济作物比粮食作物少占总量的百分比=这个农场所有作物的总质量,然后用这个农场所有作物的总质量×其他作物占总量的百分比=其他作物的质量,据此列式解答。
27.【答案】
(1)2000
(2)45
(3)伙食费900,文化教育500,表格略
补画的条形统计图如图
【解析】【解答】解:(1)一共支出:600÷30%=2000(元);
(2)1-25%-30%=45%;
(3)文化教育:2000×25%=400(元);伙食费:2000×45%=900(元),
统计表如下:
故答案为:(1)2000;(2)45。
【分析】(1)根据分数除法的意义,用其他支出的钱数除以占总支出的百分率即可求出一共支出的钱数;
(2)用1减去文化教育占的百分率和其他占的百分率即可求出伙食费支出所占的百分率;
(3)用总支出乘伙食费占的百分率求出伙食费支出数,再求出文化教育支出数,再填表;根据计算出的数据结合统计图中的数据绘制出条形统计图即可。
28.【答案】
(1)解:参加竞赛人数:36+48+30+6=120(人)
×100%=30%
×100%=40%
×100%=25%
×100%=5%
(2)
【解析】【分析】(1)根据统计图中的数据用加法计算出总人数,用优秀、良好、及格、不及格的人数分别除以总人数,分别求出各部分人数占总人数的百分率;
(2)扇形统计图中平均分成20格,每格就是5%,根据各部分占的百分率确定扇形的大小,然后画出统计图即可。
