2020-2021学年青岛新版八年级上册数学《第1章 全等三角形》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年青岛新版八年级上册数学《第1章 全等三角形》单元测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 302.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-13 21:04:45 | ||
图片预览


文档简介
2020-2021学年青岛新版八年级上册数学《第1章
全等三角形》单元测试卷
一.选择题
1.下列说法中,正确的是( )
A.面积相等的两个图形是全等图形
B.形状相等的两个图形是全等图形
C.周长相等的两个图形是全等图形
D.全等图形的面积相等
2.如图,D在△ABC的BC边上,△ABC≌△ADE,∠EAC=50°,则∠ADE的度数为( )
A.50°
B.60°
C.65°
D.70°
3.如图,AC⊥BE于点C,DF⊥BE于点F,且BC=EF,如果添上一个条件后,可以直接利用“HL”来证明△ABC≌△DEF,则这个条件应该是( )
A.AC=DE
B.AB=DE
C.∠B=∠E
D.∠D=∠A
4.如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件( )
A.∠BAC=∠BAD
B.AC=AD
C.∠ABC=∠ABD
D.以上都不正确
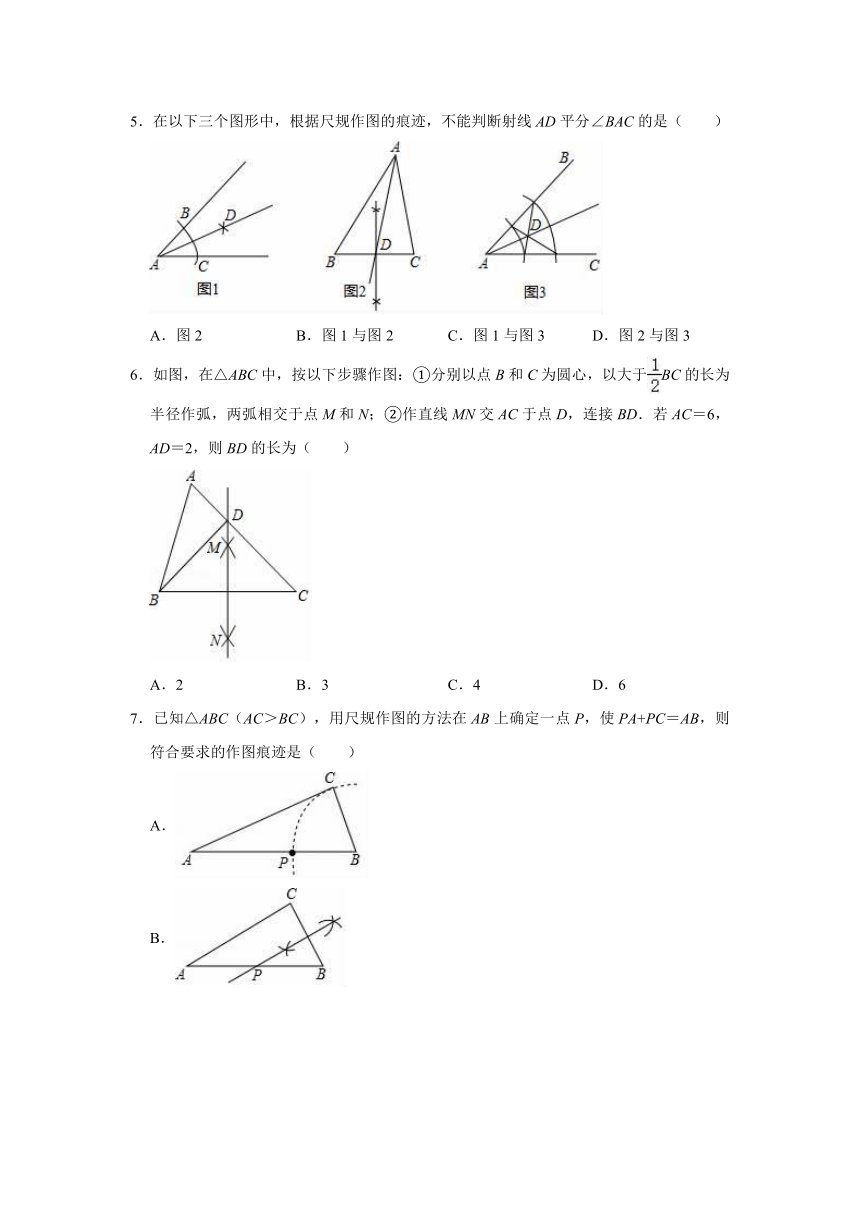
5.在以下三个图形中,根据尺规作图的痕迹,不能判断射线AD平分∠BAC的是( )
A.图2
B.图1与图2
C.图1与图3
D.图2与图3
6.如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于BC的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD.若AC=6,AD=2,则BD的长为( )
A.2
B.3
C.4
D.6
7.已知△ABC(AC>BC),用尺规作图的方法在AB上确定一点P,使PA+PC=AB,则符合要求的作图痕迹是( )
A.
B.
C.
D.
8.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为( )
A.①
B.①②
C.①②③
D.①②④
9.一块三角形的玻璃摔碎成如图所示的四块,小亮现在要带其中的一块去配成与原来一样大小的三角形玻璃,小亮去时应该带( )
A.第一块
B.第二块
C.第三块
D.第四块
10.下列作图语句正确的是( )
A.连接AD,并且平分∠BAC
B.延长射线AB
C.作∠AOB的平分线OC
D.过点A作AB∥CD∥EF
二.填空题
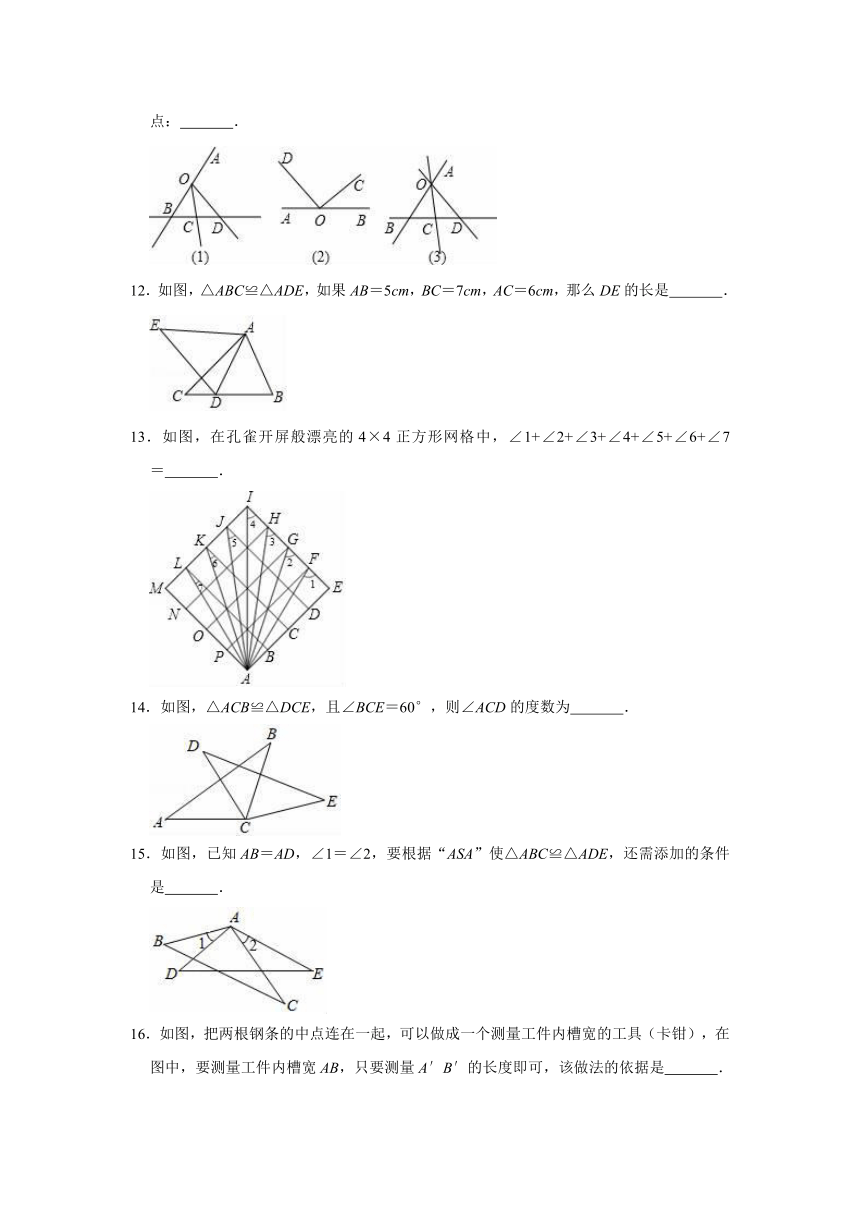
11.下列语句表示的图形是(只填序号)
①过点O的三条直线与另条一直线分别相交于点B、C、D三点:
.
②以直线AB上一点O为顶点,在直线AB的同侧画∠AOC和∠BOD:
.
③过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点:
.
12.如图,△ABC≌△ADE,如果AB=5cm,BC=7cm,AC=6cm,那么DE的长是
.
13.如图,在孔雀开屏般漂亮的4×4正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7=
.
14.如图,△ACB≌△DCE,且∠BCE=60°,则∠ACD的度数为
.
15.如图,已知AB=AD,∠1=∠2,要根据“ASA”使△ABC≌△ADE,还需添加的条件是
.
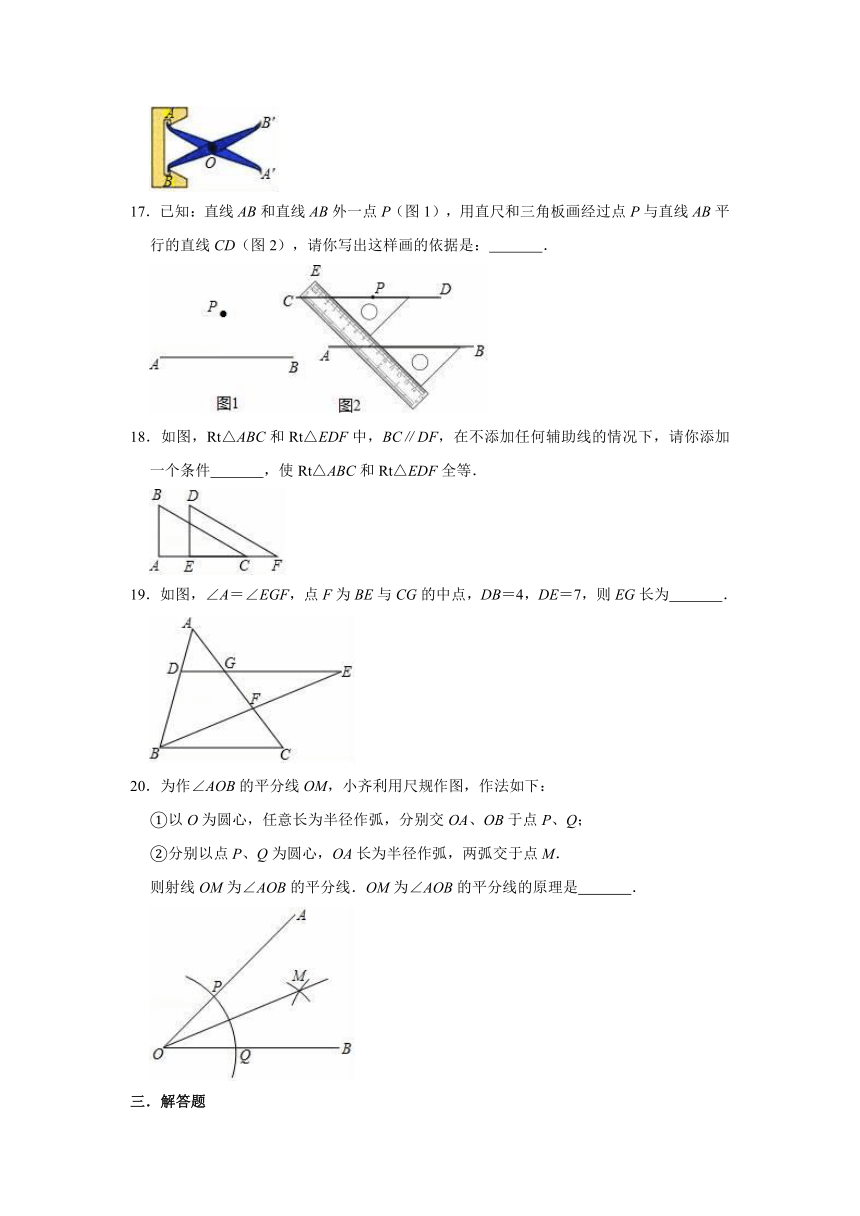
16.如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),在图中,要测量工件内槽宽AB,只要测量A′B′的长度即可,该做法的依据是
.
17.已知:直线AB和直线AB外一点P(图1),用直尺和三角板画经过点P与直线AB平行的直线CD(图2),请你写出这样画的依据是:
.
18.如图,Rt△ABC和Rt△EDF中,BC∥DF,在不添加任何辅助线的情况下,请你添加一个条件
,使Rt△ABC和Rt△EDF全等.
19.如图,∠A=∠EGF,点F为BE与CG的中点,DB=4,DE=7,则EG长为
.
20.为作∠AOB的平分线OM,小齐利用尺规作图,作法如下:
①以O为圆心,任意长为半径作弧,分别交OA、OB于点P、Q;
②分别以点P、Q为圆心,OA长为半径作弧,两弧交于点M.
则射线OM为∠AOB的平分线.OM为∠AOB的平分线的原理是
.
三.解答题
21.如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形(要求至少要画出两种方法).
22.如图,△ABC≌△DBC,∠A=40°,∠ACD=88°,求∠ABC的度数.
23.如图,已知点A,D,B,F在一条直线上,AC=FE,BC=DE,AD=FB,求证:∠A=∠F.
24.如图,A,B两点分别位于一个假山的两端,小明想用绳子测量A、B间的距离:现在地上取一个可以直接到达A点和B点的点C,连接AC并延长到点D,使CD=AC,连接BC并延长到点E,使CE=CB;连接DE并测量出它的长度.DE=8m,求AB的长度.
25.已知:如图,AB=AC,∠1=∠2,∠B=∠C.求证:△ABD≌△ACE.
26.(1)如图1,已知Rt△ABC中,∠C=90°,BC=6,AC=8,DE∥BC且DE=EB,求ED的长;
(2)如图2,已知Rt△PMN中,∠N=90°,请用尺规作图,在边PM上求点Q,使Q到边PN的距离等于Q到M的距离.
27.如图,利用尺规,在△ABC的边AC上方作∠CAE=∠ACB,在射线AE上截取AD=BC,连接CD,并证明:CD∥AB(尺规作图要求保留作图痕迹,不写作法)
参考答案与试题解析
一.选择题
1.解:A、面积相等,但图形不一定能完全重合,故本选项错误;
B、形状相等的两个图形不一定能完全重合,故本选项错误;
C、周长相等的两个图形不一定能完全重合,故本选项错误;
D、全等图形的面积相等,故本选项正确.
故选:D.
2.解:∵△ABC≌△ADE,
∴∠BAC=∠DAE,AB=AD,∠ADE=∠B,
∴∠EAC=∠DAB=50°,
∴△ABD中,∠B=(180°﹣∠BAD)=65°,
∴∠ADE=∠B=65°,
故选:C.
3.解:AB=DE,可以直接利用“HL”来证明△ABC≌△DEF.
∵AC⊥BE,DF⊥BE,
∴∠ACB=∠DFE=90°,
在Rt△ACB和Rt△DFE中,
,
∴Rt△ACB≌Rt△DFE(HL),
故选:B.
4.解:若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件AC=AD或BC=BD,
故选:B.
5.解:在图1中,利用基本作图可判断AD平分∠BAC;
在图2中,利用基本作图得到D点为BC的中点,则AD为BC边上的中线;
在图3中,利用作法得AE=AF,AM=AN,则可判断△ADM≌△ADN,所以∠AMD=∠AND,则可判断△MDE≌△NDF,所以D点到AM和AN的距离相等,则可判断AD平分∠BAC.
故选:A.
6.解:由作图知,MN是线段BC的垂直平分线,
∴BD=CD,
∵AC=6,AD=2,
∴BD=CD=4,
故选:C.
7.解:∵PA+PB=AB,PA+PC=AB,
∴PC=PB,
∴点P在BC的垂直平分线上.
故选:B.
8.解:∵∠AOB=∠COD=40°,
∴∠AOB+∠AOD=∠COD+∠AOD,
即∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
∴∠OCA=∠ODB,∠OAC=∠OBD,AC=BD,①正确;
由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,
∴∠AMB=∠AOB=40°,②正确;
作OG⊥MC于G,OH⊥MB于H,如图2所示:
则∠OGC=∠OHD=90°,
在△OCG和△ODH中,
,
∴△OCG≌△ODH(AAS),
∴OG=OH,
∴MO平分∠BMC,④正确;
∵∠AOB=∠COD,
∴当∠DOM=∠AOM时,OM才平分∠BOC,
假设∠DOM=∠AOM,
∵△AOC≌△BOD,
∴∠COM=∠BOM,
∵MO平分∠BMC,
∴∠CMO=∠BMO,
在△COM和△BOM中,
,
∴△COM≌△BOM(ASA),
∴OB=OC,
∵OA=OB,
∴OA=OC,
与OA>OC矛盾,
∴③错误;
正确的有①②④;
故选:D.
9.解:一、二、三块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第四块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.
故选:D.
10.解:A.连接AD,不能同时使平分∠BAC,此作图错误;
B.只能反向延长射线AB,此作图错误;
C.作∠AOB的平分线OC,此作图正确;
D.过点A作AB∥CD或AB∥EF,此作图错误;
故选:C.
二.填空题
11.解:①过点O的三条直线与另一条直线分别相交于点B、C、D三点的图形为(3);
②以直线AB上一点O为顶点,在直线AB的同侧画∠AOC和∠BOD的图形为(2);
③过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点的图形为(1).
故答案为:(3),(2),(1).
12.解:∵△ABC≌△ADE,BC=7,
∴DE=BC=7(cm),
故答案为:7cm.
13.解:在△AEF和△LBA中
,
∴△AEF≌△LBA(SAS),
∴∠7=∠EAF,
∴∠1+∠7=90°,
同理可得∠2+∠6=90°,∠3+∠5=90°,
而∠4=45°,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=90°+90°+90°+45°=315°.
故答案为315°.
14.解:∵△ACB≌△DCE,
∴∠ACB=∠DCE,
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,
即∠ACD=∠BCE,
∵∠BCE=60°,
∴∠ACD=60°.
故答案为:60°.
15.解:还需添加的条件是∠B=∠D,
∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE,
在△ABC和△ADE中,
∴△ABC≌△ADE(ASA),
故答案为:∠B=∠D.
16.解:连接AB,A′B′,如图,
∵点O分别是AA′、BB′的中点,
∴OA=OA′,OB=OB′,
在△AOB和△A′OB′中,
,
∴△AOB≌△A′OB′(SAS).
∴A′B′=AB.
答:需要测量A′B′的长度,即为工件内槽宽AB.
其依据是根据SAS证明△AOB≌△A′OB′;
故答案为:根据SAS证明△AOB≌△A′OB′.
17.解:根据作图过程可知:
画图的依据是:同位角相等,两直线平行.
故答案为:同位角相等,两直线平行.
18.解:∵Rt△ABC和Rt△EDF中,
∴∠BAC=∠DEF=90°,
∵BC∥DF,
∴∠DFE=∠BCA,
∴添加AB=ED,
在Rt△ABC和Rt△EDF中
,
∴Rt△ABC≌Rt△EDF(AAS),
故答案为:AB=ED(答案不唯一).
19.解:∵∠A=∠EGF,∠AGD=∠EGF,
∴∠A=∠AGD,
∴AD=DG,
设AD=x,则DG=x,
在△EGF和△BCF中,
∵,
∴△EGF≌△BCF(SAS),
∴BC=EG,∠E=∠EBC,
∴EG∥BC,
∴∠AGD=∠C=∠A,
∴BC=AB=x+4=EG,
∵DE=7,
∴x+x+4=7,
x=,
∴EG=x+4=,
故答案为:.
20.解:如图,连接PM,PQ.
∵OP=OQ,PM=QM,OM=OM,
∴△POM≌△QOM(SSS),
∴∠POM=∠QOM,即OM是∠AOB的角平分线.
故答案为SSS.
三.解答题
21.解:如图所示:
.
22.解:∵△ABC≌△DBC,
∴∠ACB=∠DCB,
∵∠ACD=88°,
∴∠ACB=44°,
∵∠A=40°,
∴∠ABC=180°﹣40°﹣44°=96°.
23.证明:∵AD=FB,
∴AD+DB=FB+DB,
即AB=FD,
在△ABC与△FDE中,
,
∴△ABC≌△FDE(SSS),
∴∠A=∠F.
24.解:在△CDE和△CAB中,CD=CA,∠DCE=∠ACB,CE=CB,
所以△CDE≌△CAB(SAS),
所以DE=AB=8m.
25.证明:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,
即∠CAE=∠BAD,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(ASA).
26.解:(1)如图1,设DE=x,
∵∠C=90°,BC=6,AC=8,
∴AB==10,
∴AE=10﹣x,
∵DE∥BC,
∴=,即=,解得x=,
即ED的长为;
(2)如图,点Q为所作.
27.解:图象如图所示,
∵∠EAC=∠ACB,
∴AD∥CB,
∵AD=BC,∠DAC=∠ACB,AC=CA,
∴△ACD≌△CAB(SAS),
∴∠ACD=∠CAB,
∴AB∥CD.
全等三角形》单元测试卷
一.选择题
1.下列说法中,正确的是( )
A.面积相等的两个图形是全等图形
B.形状相等的两个图形是全等图形
C.周长相等的两个图形是全等图形
D.全等图形的面积相等
2.如图,D在△ABC的BC边上,△ABC≌△ADE,∠EAC=50°,则∠ADE的度数为( )
A.50°
B.60°
C.65°
D.70°
3.如图,AC⊥BE于点C,DF⊥BE于点F,且BC=EF,如果添上一个条件后,可以直接利用“HL”来证明△ABC≌△DEF,则这个条件应该是( )
A.AC=DE
B.AB=DE
C.∠B=∠E
D.∠D=∠A
4.如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件( )
A.∠BAC=∠BAD
B.AC=AD
C.∠ABC=∠ABD
D.以上都不正确
5.在以下三个图形中,根据尺规作图的痕迹,不能判断射线AD平分∠BAC的是( )
A.图2
B.图1与图2
C.图1与图3
D.图2与图3
6.如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于BC的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD.若AC=6,AD=2,则BD的长为( )
A.2
B.3
C.4
D.6
7.已知△ABC(AC>BC),用尺规作图的方法在AB上确定一点P,使PA+PC=AB,则符合要求的作图痕迹是( )
A.
B.
C.
D.
8.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为( )
A.①
B.①②
C.①②③
D.①②④
9.一块三角形的玻璃摔碎成如图所示的四块,小亮现在要带其中的一块去配成与原来一样大小的三角形玻璃,小亮去时应该带( )
A.第一块
B.第二块
C.第三块
D.第四块
10.下列作图语句正确的是( )
A.连接AD,并且平分∠BAC
B.延长射线AB
C.作∠AOB的平分线OC
D.过点A作AB∥CD∥EF
二.填空题
11.下列语句表示的图形是(只填序号)
①过点O的三条直线与另条一直线分别相交于点B、C、D三点:
.
②以直线AB上一点O为顶点,在直线AB的同侧画∠AOC和∠BOD:
.
③过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点:
.
12.如图,△ABC≌△ADE,如果AB=5cm,BC=7cm,AC=6cm,那么DE的长是
.
13.如图,在孔雀开屏般漂亮的4×4正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7=
.
14.如图,△ACB≌△DCE,且∠BCE=60°,则∠ACD的度数为
.
15.如图,已知AB=AD,∠1=∠2,要根据“ASA”使△ABC≌△ADE,还需添加的条件是
.
16.如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),在图中,要测量工件内槽宽AB,只要测量A′B′的长度即可,该做法的依据是
.
17.已知:直线AB和直线AB外一点P(图1),用直尺和三角板画经过点P与直线AB平行的直线CD(图2),请你写出这样画的依据是:
.
18.如图,Rt△ABC和Rt△EDF中,BC∥DF,在不添加任何辅助线的情况下,请你添加一个条件
,使Rt△ABC和Rt△EDF全等.
19.如图,∠A=∠EGF,点F为BE与CG的中点,DB=4,DE=7,则EG长为
.
20.为作∠AOB的平分线OM,小齐利用尺规作图,作法如下:
①以O为圆心,任意长为半径作弧,分别交OA、OB于点P、Q;
②分别以点P、Q为圆心,OA长为半径作弧,两弧交于点M.
则射线OM为∠AOB的平分线.OM为∠AOB的平分线的原理是
.
三.解答题
21.如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形(要求至少要画出两种方法).
22.如图,△ABC≌△DBC,∠A=40°,∠ACD=88°,求∠ABC的度数.
23.如图,已知点A,D,B,F在一条直线上,AC=FE,BC=DE,AD=FB,求证:∠A=∠F.
24.如图,A,B两点分别位于一个假山的两端,小明想用绳子测量A、B间的距离:现在地上取一个可以直接到达A点和B点的点C,连接AC并延长到点D,使CD=AC,连接BC并延长到点E,使CE=CB;连接DE并测量出它的长度.DE=8m,求AB的长度.
25.已知:如图,AB=AC,∠1=∠2,∠B=∠C.求证:△ABD≌△ACE.
26.(1)如图1,已知Rt△ABC中,∠C=90°,BC=6,AC=8,DE∥BC且DE=EB,求ED的长;
(2)如图2,已知Rt△PMN中,∠N=90°,请用尺规作图,在边PM上求点Q,使Q到边PN的距离等于Q到M的距离.
27.如图,利用尺规,在△ABC的边AC上方作∠CAE=∠ACB,在射线AE上截取AD=BC,连接CD,并证明:CD∥AB(尺规作图要求保留作图痕迹,不写作法)
参考答案与试题解析
一.选择题
1.解:A、面积相等,但图形不一定能完全重合,故本选项错误;
B、形状相等的两个图形不一定能完全重合,故本选项错误;
C、周长相等的两个图形不一定能完全重合,故本选项错误;
D、全等图形的面积相等,故本选项正确.
故选:D.
2.解:∵△ABC≌△ADE,
∴∠BAC=∠DAE,AB=AD,∠ADE=∠B,
∴∠EAC=∠DAB=50°,
∴△ABD中,∠B=(180°﹣∠BAD)=65°,
∴∠ADE=∠B=65°,
故选:C.
3.解:AB=DE,可以直接利用“HL”来证明△ABC≌△DEF.
∵AC⊥BE,DF⊥BE,
∴∠ACB=∠DFE=90°,
在Rt△ACB和Rt△DFE中,
,
∴Rt△ACB≌Rt△DFE(HL),
故选:B.
4.解:若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件AC=AD或BC=BD,
故选:B.
5.解:在图1中,利用基本作图可判断AD平分∠BAC;
在图2中,利用基本作图得到D点为BC的中点,则AD为BC边上的中线;
在图3中,利用作法得AE=AF,AM=AN,则可判断△ADM≌△ADN,所以∠AMD=∠AND,则可判断△MDE≌△NDF,所以D点到AM和AN的距离相等,则可判断AD平分∠BAC.
故选:A.
6.解:由作图知,MN是线段BC的垂直平分线,
∴BD=CD,
∵AC=6,AD=2,
∴BD=CD=4,
故选:C.
7.解:∵PA+PB=AB,PA+PC=AB,
∴PC=PB,
∴点P在BC的垂直平分线上.
故选:B.
8.解:∵∠AOB=∠COD=40°,
∴∠AOB+∠AOD=∠COD+∠AOD,
即∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
∴∠OCA=∠ODB,∠OAC=∠OBD,AC=BD,①正确;
由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,
∴∠AMB=∠AOB=40°,②正确;
作OG⊥MC于G,OH⊥MB于H,如图2所示:
则∠OGC=∠OHD=90°,
在△OCG和△ODH中,
,
∴△OCG≌△ODH(AAS),
∴OG=OH,
∴MO平分∠BMC,④正确;
∵∠AOB=∠COD,
∴当∠DOM=∠AOM时,OM才平分∠BOC,
假设∠DOM=∠AOM,
∵△AOC≌△BOD,
∴∠COM=∠BOM,
∵MO平分∠BMC,
∴∠CMO=∠BMO,
在△COM和△BOM中,
,
∴△COM≌△BOM(ASA),
∴OB=OC,
∵OA=OB,
∴OA=OC,
与OA>OC矛盾,
∴③错误;
正确的有①②④;
故选:D.
9.解:一、二、三块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第四块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.
故选:D.
10.解:A.连接AD,不能同时使平分∠BAC,此作图错误;
B.只能反向延长射线AB,此作图错误;
C.作∠AOB的平分线OC,此作图正确;
D.过点A作AB∥CD或AB∥EF,此作图错误;
故选:C.
二.填空题
11.解:①过点O的三条直线与另一条直线分别相交于点B、C、D三点的图形为(3);
②以直线AB上一点O为顶点,在直线AB的同侧画∠AOC和∠BOD的图形为(2);
③过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点的图形为(1).
故答案为:(3),(2),(1).
12.解:∵△ABC≌△ADE,BC=7,
∴DE=BC=7(cm),
故答案为:7cm.
13.解:在△AEF和△LBA中
,
∴△AEF≌△LBA(SAS),
∴∠7=∠EAF,
∴∠1+∠7=90°,
同理可得∠2+∠6=90°,∠3+∠5=90°,
而∠4=45°,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=90°+90°+90°+45°=315°.
故答案为315°.
14.解:∵△ACB≌△DCE,
∴∠ACB=∠DCE,
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,
即∠ACD=∠BCE,
∵∠BCE=60°,
∴∠ACD=60°.
故答案为:60°.
15.解:还需添加的条件是∠B=∠D,
∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE,
在△ABC和△ADE中,
∴△ABC≌△ADE(ASA),
故答案为:∠B=∠D.
16.解:连接AB,A′B′,如图,
∵点O分别是AA′、BB′的中点,
∴OA=OA′,OB=OB′,
在△AOB和△A′OB′中,
,
∴△AOB≌△A′OB′(SAS).
∴A′B′=AB.
答:需要测量A′B′的长度,即为工件内槽宽AB.
其依据是根据SAS证明△AOB≌△A′OB′;
故答案为:根据SAS证明△AOB≌△A′OB′.
17.解:根据作图过程可知:
画图的依据是:同位角相等,两直线平行.
故答案为:同位角相等,两直线平行.
18.解:∵Rt△ABC和Rt△EDF中,
∴∠BAC=∠DEF=90°,
∵BC∥DF,
∴∠DFE=∠BCA,
∴添加AB=ED,
在Rt△ABC和Rt△EDF中
,
∴Rt△ABC≌Rt△EDF(AAS),
故答案为:AB=ED(答案不唯一).
19.解:∵∠A=∠EGF,∠AGD=∠EGF,
∴∠A=∠AGD,
∴AD=DG,
设AD=x,则DG=x,
在△EGF和△BCF中,
∵,
∴△EGF≌△BCF(SAS),
∴BC=EG,∠E=∠EBC,
∴EG∥BC,
∴∠AGD=∠C=∠A,
∴BC=AB=x+4=EG,
∵DE=7,
∴x+x+4=7,
x=,
∴EG=x+4=,
故答案为:.
20.解:如图,连接PM,PQ.
∵OP=OQ,PM=QM,OM=OM,
∴△POM≌△QOM(SSS),
∴∠POM=∠QOM,即OM是∠AOB的角平分线.
故答案为SSS.
三.解答题
21.解:如图所示:
.
22.解:∵△ABC≌△DBC,
∴∠ACB=∠DCB,
∵∠ACD=88°,
∴∠ACB=44°,
∵∠A=40°,
∴∠ABC=180°﹣40°﹣44°=96°.
23.证明:∵AD=FB,
∴AD+DB=FB+DB,
即AB=FD,
在△ABC与△FDE中,
,
∴△ABC≌△FDE(SSS),
∴∠A=∠F.
24.解:在△CDE和△CAB中,CD=CA,∠DCE=∠ACB,CE=CB,
所以△CDE≌△CAB(SAS),
所以DE=AB=8m.
25.证明:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,
即∠CAE=∠BAD,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(ASA).
26.解:(1)如图1,设DE=x,
∵∠C=90°,BC=6,AC=8,
∴AB==10,
∴AE=10﹣x,
∵DE∥BC,
∴=,即=,解得x=,
即ED的长为;
(2)如图,点Q为所作.
27.解:图象如图所示,
∵∠EAC=∠ACB,
∴AD∥CB,
∵AD=BC,∠DAC=∠ACB,AC=CA,
∴△ACD≌△CAB(SAS),
∴∠ACD=∠CAB,
∴AB∥CD.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
