2020-2021学年青岛新版八年级上册数学《第4章 数据分析》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年青岛新版八年级上册数学《第4章 数据分析》单元测试卷(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 216.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-13 00:00:00 | ||
图片预览



文档简介
2020-2021学年青岛新版八年级上册数学《第4章
数据分析》单元测试卷
一.选择题
1.某地区100个家庭的收入从低到高是4800元,…,10000元各不相同,在输入计算机时,把最大的数据错误地输成100000元,则依据错误的数字算出的平均值与实际数字的平均值的差是( )
A.900元
B.942元
C.90
000元
D.1
000元
2.某公司有15名员工,他们所在的部门及相应每人所创的年利润(单位:万元)如下表所示:
部门
A
B
C
D
E
F
G
人数
1
1
2
4
2
2
3
年利润
20
5
2.5
2.1
1.5
1.5
1.2
则该公司每人所创年利润的平均值为( )
A.2.25万元
B.4.83万元
C.3.2万元
D.3.3万元
3.一次体检中,某班学生视力检查的结果如图所示,从图中看出全班视力数据的众数是( )
A.55%
B.24%
C.1.0
D.1.0以上
4.天气预报说今天最高气温为27℃,最低气温是15℃,则今天气温的极差是( )
A.12℃
B.19℃
C.32℃
D.﹣12℃
5.一组数据12,8,11,9,x的平均数是10,则数据的标准差是( )
A.1
B.
C.
D.2
6.九年级(1)、(2)两班在一次数学考试中,成绩的平均数相同,但(1)班的成绩比(2)班整齐,若(1)、(2)两班成绩的方差分别为S12和S22,则( )
A.S12>S22
B.S12<S22
C.S12=S22
D.S12与S22无法比较大小
7.某同学用计算器计算30个数据时,错将其中一个数据105输入15,那么由此求出的平均数与实际平均数的差是( )
A.3.5
B.3
C.﹣3
D.0.5
8.有m个数的平均值是x,n个数的平均值是y,则这m+n个数的平均值是( )
A.
B.
C.
D.x+y
9.由小到大排列一组数据a1,a2,a3,a4,a5,其中每个数据都小于0,则对于样本a1,a2,﹣a3,﹣a4,﹣a5,0的中位数可表示为( )
A.
B.
C.
D.
10.一组数据12,20,23,14,16,27,30,x,它的中位数是20.5,则x的值是( )
A.小于21的数
B.20.5
C.21
D.以上答案都不对
二.填空题
11.小明去超市买了三种糖果,其价格分别是10元/千克,13元/千克和16元/千克,他分别买了3千克,2千克和1千克,将其混合组成什锦糖,那么这种什锦糖的价格是
元/千克.
12.学校组织领导、教师、学生、家长等人对教师的工作表现进行综合评分,满分为100分,张老师的得分情况如下:领导平均给分90分,教师平均给分87分,学生平均给分92分,家长平均给分90分,如果按照1:2:4:1的权重进行计算,那么张老师的综合评分应为
分.
13.在对某地区一次人口抽样统计中,各年龄段的人数如表所示(单位:岁,年龄为整数),请根据此表回答下列问题:
年龄
0﹣9
10﹣19
20﹣29
30﹣39
40﹣49
50﹣59
60﹣69
70﹣79
80﹣89
人数
9
11
17
18
17
12
8
6
2
在这个样本中,年龄的中位数位于
岁年龄段内在.
14.一组数据按从小到大的顺序排列为:13、14、19、x、23、27、28、31,其中位数是22,则x为
.
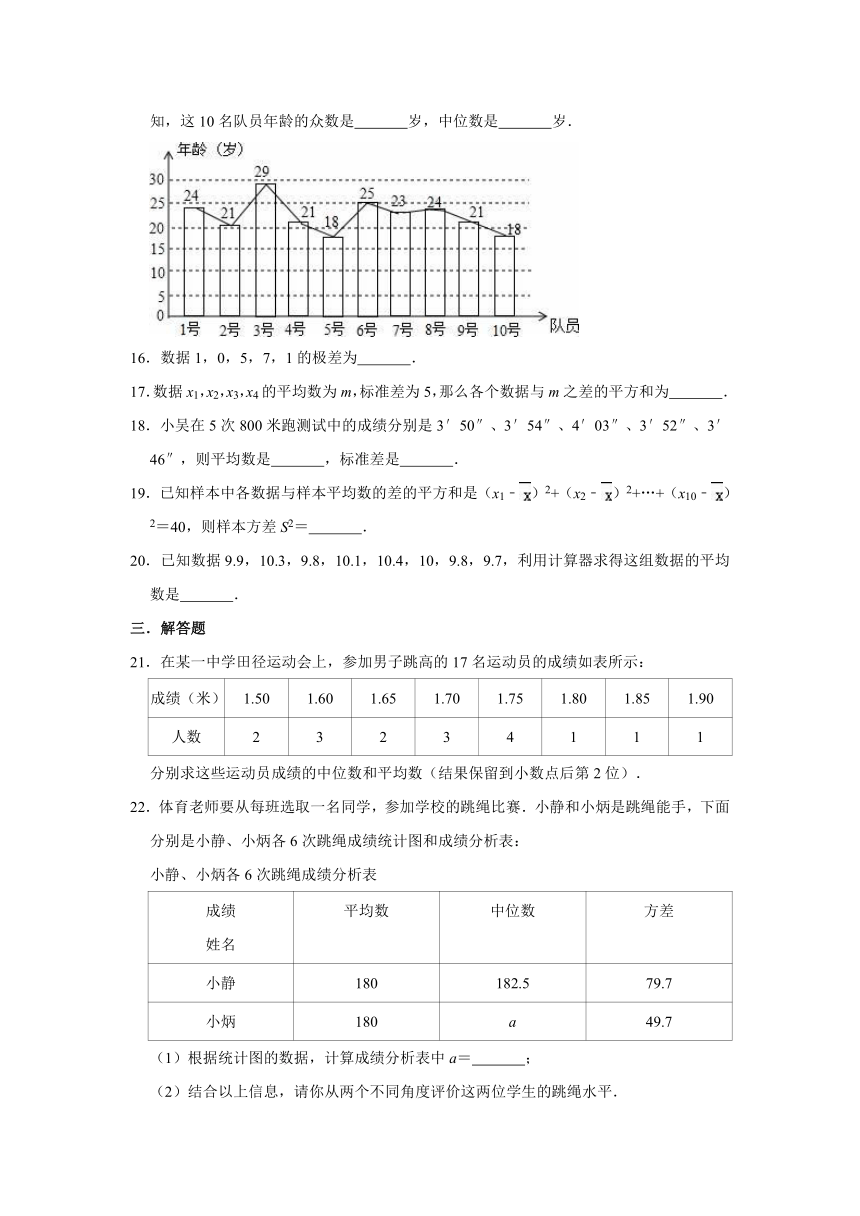
15.如图所示是2012~2013赛季国内某足球队1~10号队员的年龄统计图,根据统计图可知,这10名队员年龄的众数是
岁,中位数是
岁.
16.数据1,0,5,7,1的极差为
.
17.数据x1,x2,x3,x4的平均数为m,标准差为5,那么各个数据与m之差的平方和为
.
18.小吴在5次800米跑测试中的成绩分别是3′50″、3′54″、4′03″、3′52″、3′46″,则平均数是
,标准差是
.
19.已知样本中各数据与样本平均数的差的平方和是(x1﹣)2+(x2﹣)2+…+(x10﹣)2=40,则样本方差S2=
.
20.已知数据9.9,10.3,9.8,10.1,10.4,10,9.8,9.7,利用计算器求得这组数据的平均数是
.
三.解答题
21.在某一中学田径运动会上,参加男子跳高的17名运动员的成绩如表所示:
成绩(米)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
分别求这些运动员成绩的中位数和平均数(结果保留到小数点后第2位).
22.体育老师要从每班选取一名同学,参加学校的跳绳比赛.小静和小炳是跳绳能手,下面分别是小静、小炳各6次跳绳成绩统计图和成绩分析表:
小静、小炳各6次跳绳成绩分析表
成绩姓名
平均数
中位数
方差
小静
180
182.5
79.7
小炳
180
a
49.7
(1)根据统计图的数据,计算成绩分析表中a=
;
(2)结合以上信息,请你从两个不同角度评价这两位学生的跳绳水平.
23.某校对三个年级的卫生检查情况(单位:分)如下:
黑板
门窗
桌椅
地面
七年级
95
90
80
95
八年级
90
95
85
90
九年级
85
90
95
90
(1)试计算各年级卫生平均成绩,并说明哪个年级卫生状况最好?
(2)若学校规定黑板、门窗、桌椅、地面这四项得分依次按15%,10%,35%,40%的比例计算各年级的卫生成绩来评选卫生先进年级,问哪个年级当选?
24.张老师想对同学们的打字能力进行测试,他将全班同学分成5组.经统计,这5个小组平均每分钟打字的个数如下:100,80,x,90,90.已知这组数据的众数与平均数相等,那么这组数据中的未知数x是多少?
25.已知数据:10、10、x、8的中位数与平均数相等,求这组数据的中位数.
26.下表是甲、乙两人各打靶十次的成绩情况统计表(单位:环)
一
二
三
四
五
六
七
八
九
十
甲
9
5
7
8
7
7
8
6
7
7
乙
2
4
6
8
7
6
8
9
9
10
根据上面的统计表,制作适当的统计图表示甲、乙两人打靶成绩的变化,并回答下列问题.
(1)谁成绩变化的幅度大?
(2)甲、乙两人哪一次射击的成绩相差最大?相差多少?
参考答案与试题解析
一.选择题
1.解:设除家庭收入为10000元的另外99个家庭收入的和为a元,
把最大的数10000错误地输成100000元时这100个家庭收入的平均值为=(+1000)(元),
实际这100个家庭收入的平均值为=(+100)(元),
则(+1000)﹣(+100)=900(元).
故选:A.
2.解:根据题意得:
==3.2(万元);
答:该公司每人所创年利润的平均值为3.2万元.
故选:C.
3.解:众数是一组数据中出现次数最多的数据,1.0占全班人数的55%,故1.0是众数.
故选:C.
4.解:今天气温的极差是12℃.
故选:A.
5.解:依题意得:x=5×10﹣12﹣8﹣11﹣9=10
方差S2=
[(12﹣10)2+(8﹣10)2+(11﹣10)2+(9﹣10)2+(10﹣10)2]=2
所以标准差=.
故选:B.
6.解:∵甲乙两校的成绩平均分相同,但甲校的成绩比乙校整齐,
∴甲校的方差比乙校的成绩方差小即S12<S22.
故选:B.
7.解:求30个数据的平均数时,错将其中的一个数据105输入成15,即少加了90;
则由此求出的平均数与实际平均数的差是:
﹣=﹣3.
故选:C.
8.解:∵m个数的平均值是x,n个数的平均值是y,
∴这m+n个数的平均值是;
故选:C.
9.解:因为a1<a2<a3<a4<a5<0,所以a1<a2<0<﹣a5<﹣a4<﹣a3,所以中位数为.
故选:C.
10.解:根据题意这组数据从小到大的顺序排列有三种情况:
(1)12,14,16,20,x,23,27,30中,中位数为(20+x)÷2=20.5,x=21;
(2)x,12,14,16,20,23,27,30中,中位数为(16+20)÷2=18,与题意不符;
(3)12,14,16,20,23,27,30,x中,中位数为(23+20)÷2=,与题意不符.
故选:C.
二.填空题
11.解:由题可得,这种什锦糖的价格为:
=12(元/千克).
故答案为:12.
12.解:==90.25(分).
故答案为:90.25.
13.解:由题意可得,样本容量是100,
根据表格可以知道中位数在30~39岁年龄段内.
故答案为:30~39.
14.解:按从小到大的顺序排列:13、14、19、x、23、27、28、31,
所以x=22×2﹣23=21;
故答案为:21.
15.解:如图所示:
年龄/岁
18
21
23
24
25
29
人数/人
2
3
1
2
1
1
中位数是:
(21+23)÷2,
=44÷2,
=22,
众数是21;
答:中位数是22,众数是21.
故答案为:21,22.
16.解:极差=7﹣0=7.
故答案为7.
17.解:∵数据x1,x2,x3,x4的平均数为m,标准差为5,
∴
[(x1﹣m)2+(x2﹣m)2+(x3﹣m)2+(x4﹣m)2]=25,
∴(x1﹣m)2+(x2﹣m)2+(x3﹣m)2+(x4﹣m)2=100;
故答案为:100.
18.解:(3′50″+3′54″+4′03″+3′52″+3′46″)=3′53″,
方差S2=
[(3′50″﹣3′53″)2+…+(3′46″﹣3′53″)2]=32,
故标准差是S==4′.
故答案为:3′53″;4′.
19.解:S2=
[(x1﹣)2+(x2﹣)2+…+(x10﹣)2]==4.
故答案为:4.
20.解:利用计算器计算平均数=(9.9+10.3+9.8+10.1+10.4+10+9.8+9.7)=10.
故填10.
三.解答题
21.解:本题中人数的总个数是17人,奇数,从小到大排列后第9名运动员的成绩是1.70(米);
平均数是:(1.50×2+1.60×3+1.65×2+1.70×3+1.75×4+1.80+1.85+1.90)÷17
=(3+4.8+3.3+5.1+7+1.8+1.85+1.9)÷17
=28.75÷17
≈1.69(米),
答:这些运动员成绩的中位数是1.70米,平均数大约是1.69米.
22.解:(1)成绩分析表中a==179,
故答案为:179;
(2)从中位数看,小静的中位数大于小炳的中位数,所以小静取得高分可能性较大;
从方差看,小炳的方差小于小静的方差,所以小炳成绩更为稳定.
23.解:(1)∵七年级的平均成绩=(95+90+80+95)÷4=90,
八年级的平均成绩=(90+95+85+90)÷4=90,
九年级的平均成绩=(85+90+95+90)÷4=90,
∴三个年级的卫生状况都很好;
(2)∵七年级的加权平均成绩=95×15%+90×10%+80×35%+95×40%=89.25,
八年级的加权平均成绩=90×15%+95×10%+85×35%+90×40%=88.75,
九年级的加权平均成绩=85×15%+90×10%+95×35%+90×40%=91,
∴九年级的成绩最高,九年级应当选;
24.解:∵100,80,x,90,90,
∴分为3种情况:①当众数是90时,
∵这组数据的众数与平均数相等,
∴=90,
解得:x=90;
②当众数是80时,即x=80,
∵这组数据的众数与平均数相等,
∴≠80,
∴此时不行;
③当众数是100时,即x=100,
∵这组数据的众数与平均数相等,
∴=≠100,
∴此时不行;
故这组数据中的未知数x是90.
25.解:这一组数据的平均数为=,因该组数据只有4个,
故中位数应为将该组数据按从小到大顺序排列,处于最中间两个数的平均数,由于不知道x的具体数值,所以要分情况讨论:
(1)当x≤8时,该组数据从小到大顺序排列应为:x、8、10、10,
这时中位数为9,则=9,解得x=8,所以此时中位数为9;
(2)当8<x≤10时,该组数据从小到大顺序排列应为:8、x、10、10,
这时中位数为,则,解得x=8,不在8<x≤10内,此时x不存在;
(3)当x≥10时,该组数据从小到大顺序排列应为:8、10、10、x,
这时中位数为10,则,解得x=12,所以此时中位数为10;
综上所述,这组数据的中位数为9或10
26.解:
(1)∵甲中找出数据中最大的值9,最小值5,故极差是4,
乙中找出数据中最大的值10,最小值2,极差是8,
∴乙成绩变化的幅度大;
(2)从数据中找出成绩相差大的是第一次,相差9﹣2=7环.
数据分析》单元测试卷
一.选择题
1.某地区100个家庭的收入从低到高是4800元,…,10000元各不相同,在输入计算机时,把最大的数据错误地输成100000元,则依据错误的数字算出的平均值与实际数字的平均值的差是( )
A.900元
B.942元
C.90
000元
D.1
000元
2.某公司有15名员工,他们所在的部门及相应每人所创的年利润(单位:万元)如下表所示:
部门
A
B
C
D
E
F
G
人数
1
1
2
4
2
2
3
年利润
20
5
2.5
2.1
1.5
1.5
1.2
则该公司每人所创年利润的平均值为( )
A.2.25万元
B.4.83万元
C.3.2万元
D.3.3万元
3.一次体检中,某班学生视力检查的结果如图所示,从图中看出全班视力数据的众数是( )
A.55%
B.24%
C.1.0
D.1.0以上
4.天气预报说今天最高气温为27℃,最低气温是15℃,则今天气温的极差是( )
A.12℃
B.19℃
C.32℃
D.﹣12℃
5.一组数据12,8,11,9,x的平均数是10,则数据的标准差是( )
A.1
B.
C.
D.2
6.九年级(1)、(2)两班在一次数学考试中,成绩的平均数相同,但(1)班的成绩比(2)班整齐,若(1)、(2)两班成绩的方差分别为S12和S22,则( )
A.S12>S22
B.S12<S22
C.S12=S22
D.S12与S22无法比较大小
7.某同学用计算器计算30个数据时,错将其中一个数据105输入15,那么由此求出的平均数与实际平均数的差是( )
A.3.5
B.3
C.﹣3
D.0.5
8.有m个数的平均值是x,n个数的平均值是y,则这m+n个数的平均值是( )
A.
B.
C.
D.x+y
9.由小到大排列一组数据a1,a2,a3,a4,a5,其中每个数据都小于0,则对于样本a1,a2,﹣a3,﹣a4,﹣a5,0的中位数可表示为( )
A.
B.
C.
D.
10.一组数据12,20,23,14,16,27,30,x,它的中位数是20.5,则x的值是( )
A.小于21的数
B.20.5
C.21
D.以上答案都不对
二.填空题
11.小明去超市买了三种糖果,其价格分别是10元/千克,13元/千克和16元/千克,他分别买了3千克,2千克和1千克,将其混合组成什锦糖,那么这种什锦糖的价格是
元/千克.
12.学校组织领导、教师、学生、家长等人对教师的工作表现进行综合评分,满分为100分,张老师的得分情况如下:领导平均给分90分,教师平均给分87分,学生平均给分92分,家长平均给分90分,如果按照1:2:4:1的权重进行计算,那么张老师的综合评分应为
分.
13.在对某地区一次人口抽样统计中,各年龄段的人数如表所示(单位:岁,年龄为整数),请根据此表回答下列问题:
年龄
0﹣9
10﹣19
20﹣29
30﹣39
40﹣49
50﹣59
60﹣69
70﹣79
80﹣89
人数
9
11
17
18
17
12
8
6
2
在这个样本中,年龄的中位数位于
岁年龄段内在.
14.一组数据按从小到大的顺序排列为:13、14、19、x、23、27、28、31,其中位数是22,则x为
.
15.如图所示是2012~2013赛季国内某足球队1~10号队员的年龄统计图,根据统计图可知,这10名队员年龄的众数是
岁,中位数是
岁.
16.数据1,0,5,7,1的极差为
.
17.数据x1,x2,x3,x4的平均数为m,标准差为5,那么各个数据与m之差的平方和为
.
18.小吴在5次800米跑测试中的成绩分别是3′50″、3′54″、4′03″、3′52″、3′46″,则平均数是
,标准差是
.
19.已知样本中各数据与样本平均数的差的平方和是(x1﹣)2+(x2﹣)2+…+(x10﹣)2=40,则样本方差S2=
.
20.已知数据9.9,10.3,9.8,10.1,10.4,10,9.8,9.7,利用计算器求得这组数据的平均数是
.
三.解答题
21.在某一中学田径运动会上,参加男子跳高的17名运动员的成绩如表所示:
成绩(米)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
分别求这些运动员成绩的中位数和平均数(结果保留到小数点后第2位).
22.体育老师要从每班选取一名同学,参加学校的跳绳比赛.小静和小炳是跳绳能手,下面分别是小静、小炳各6次跳绳成绩统计图和成绩分析表:
小静、小炳各6次跳绳成绩分析表
成绩姓名
平均数
中位数
方差
小静
180
182.5
79.7
小炳
180
a
49.7
(1)根据统计图的数据,计算成绩分析表中a=
;
(2)结合以上信息,请你从两个不同角度评价这两位学生的跳绳水平.
23.某校对三个年级的卫生检查情况(单位:分)如下:
黑板
门窗
桌椅
地面
七年级
95
90
80
95
八年级
90
95
85
90
九年级
85
90
95
90
(1)试计算各年级卫生平均成绩,并说明哪个年级卫生状况最好?
(2)若学校规定黑板、门窗、桌椅、地面这四项得分依次按15%,10%,35%,40%的比例计算各年级的卫生成绩来评选卫生先进年级,问哪个年级当选?
24.张老师想对同学们的打字能力进行测试,他将全班同学分成5组.经统计,这5个小组平均每分钟打字的个数如下:100,80,x,90,90.已知这组数据的众数与平均数相等,那么这组数据中的未知数x是多少?
25.已知数据:10、10、x、8的中位数与平均数相等,求这组数据的中位数.
26.下表是甲、乙两人各打靶十次的成绩情况统计表(单位:环)
一
二
三
四
五
六
七
八
九
十
甲
9
5
7
8
7
7
8
6
7
7
乙
2
4
6
8
7
6
8
9
9
10
根据上面的统计表,制作适当的统计图表示甲、乙两人打靶成绩的变化,并回答下列问题.
(1)谁成绩变化的幅度大?
(2)甲、乙两人哪一次射击的成绩相差最大?相差多少?
参考答案与试题解析
一.选择题
1.解:设除家庭收入为10000元的另外99个家庭收入的和为a元,
把最大的数10000错误地输成100000元时这100个家庭收入的平均值为=(+1000)(元),
实际这100个家庭收入的平均值为=(+100)(元),
则(+1000)﹣(+100)=900(元).
故选:A.
2.解:根据题意得:
==3.2(万元);
答:该公司每人所创年利润的平均值为3.2万元.
故选:C.
3.解:众数是一组数据中出现次数最多的数据,1.0占全班人数的55%,故1.0是众数.
故选:C.
4.解:今天气温的极差是12℃.
故选:A.
5.解:依题意得:x=5×10﹣12﹣8﹣11﹣9=10
方差S2=
[(12﹣10)2+(8﹣10)2+(11﹣10)2+(9﹣10)2+(10﹣10)2]=2
所以标准差=.
故选:B.
6.解:∵甲乙两校的成绩平均分相同,但甲校的成绩比乙校整齐,
∴甲校的方差比乙校的成绩方差小即S12<S22.
故选:B.
7.解:求30个数据的平均数时,错将其中的一个数据105输入成15,即少加了90;
则由此求出的平均数与实际平均数的差是:
﹣=﹣3.
故选:C.
8.解:∵m个数的平均值是x,n个数的平均值是y,
∴这m+n个数的平均值是;
故选:C.
9.解:因为a1<a2<a3<a4<a5<0,所以a1<a2<0<﹣a5<﹣a4<﹣a3,所以中位数为.
故选:C.
10.解:根据题意这组数据从小到大的顺序排列有三种情况:
(1)12,14,16,20,x,23,27,30中,中位数为(20+x)÷2=20.5,x=21;
(2)x,12,14,16,20,23,27,30中,中位数为(16+20)÷2=18,与题意不符;
(3)12,14,16,20,23,27,30,x中,中位数为(23+20)÷2=,与题意不符.
故选:C.
二.填空题
11.解:由题可得,这种什锦糖的价格为:
=12(元/千克).
故答案为:12.
12.解:==90.25(分).
故答案为:90.25.
13.解:由题意可得,样本容量是100,
根据表格可以知道中位数在30~39岁年龄段内.
故答案为:30~39.
14.解:按从小到大的顺序排列:13、14、19、x、23、27、28、31,
所以x=22×2﹣23=21;
故答案为:21.
15.解:如图所示:
年龄/岁
18
21
23
24
25
29
人数/人
2
3
1
2
1
1
中位数是:
(21+23)÷2,
=44÷2,
=22,
众数是21;
答:中位数是22,众数是21.
故答案为:21,22.
16.解:极差=7﹣0=7.
故答案为7.
17.解:∵数据x1,x2,x3,x4的平均数为m,标准差为5,
∴
[(x1﹣m)2+(x2﹣m)2+(x3﹣m)2+(x4﹣m)2]=25,
∴(x1﹣m)2+(x2﹣m)2+(x3﹣m)2+(x4﹣m)2=100;
故答案为:100.
18.解:(3′50″+3′54″+4′03″+3′52″+3′46″)=3′53″,
方差S2=
[(3′50″﹣3′53″)2+…+(3′46″﹣3′53″)2]=32,
故标准差是S==4′.
故答案为:3′53″;4′.
19.解:S2=
[(x1﹣)2+(x2﹣)2+…+(x10﹣)2]==4.
故答案为:4.
20.解:利用计算器计算平均数=(9.9+10.3+9.8+10.1+10.4+10+9.8+9.7)=10.
故填10.
三.解答题
21.解:本题中人数的总个数是17人,奇数,从小到大排列后第9名运动员的成绩是1.70(米);
平均数是:(1.50×2+1.60×3+1.65×2+1.70×3+1.75×4+1.80+1.85+1.90)÷17
=(3+4.8+3.3+5.1+7+1.8+1.85+1.9)÷17
=28.75÷17
≈1.69(米),
答:这些运动员成绩的中位数是1.70米,平均数大约是1.69米.
22.解:(1)成绩分析表中a==179,
故答案为:179;
(2)从中位数看,小静的中位数大于小炳的中位数,所以小静取得高分可能性较大;
从方差看,小炳的方差小于小静的方差,所以小炳成绩更为稳定.
23.解:(1)∵七年级的平均成绩=(95+90+80+95)÷4=90,
八年级的平均成绩=(90+95+85+90)÷4=90,
九年级的平均成绩=(85+90+95+90)÷4=90,
∴三个年级的卫生状况都很好;
(2)∵七年级的加权平均成绩=95×15%+90×10%+80×35%+95×40%=89.25,
八年级的加权平均成绩=90×15%+95×10%+85×35%+90×40%=88.75,
九年级的加权平均成绩=85×15%+90×10%+95×35%+90×40%=91,
∴九年级的成绩最高,九年级应当选;
24.解:∵100,80,x,90,90,
∴分为3种情况:①当众数是90时,
∵这组数据的众数与平均数相等,
∴=90,
解得:x=90;
②当众数是80时,即x=80,
∵这组数据的众数与平均数相等,
∴≠80,
∴此时不行;
③当众数是100时,即x=100,
∵这组数据的众数与平均数相等,
∴=≠100,
∴此时不行;
故这组数据中的未知数x是90.
25.解:这一组数据的平均数为=,因该组数据只有4个,
故中位数应为将该组数据按从小到大顺序排列,处于最中间两个数的平均数,由于不知道x的具体数值,所以要分情况讨论:
(1)当x≤8时,该组数据从小到大顺序排列应为:x、8、10、10,
这时中位数为9,则=9,解得x=8,所以此时中位数为9;
(2)当8<x≤10时,该组数据从小到大顺序排列应为:8、x、10、10,
这时中位数为,则,解得x=8,不在8<x≤10内,此时x不存在;
(3)当x≥10时,该组数据从小到大顺序排列应为:8、10、10、x,
这时中位数为10,则,解得x=12,所以此时中位数为10;
综上所述,这组数据的中位数为9或10
26.解:
(1)∵甲中找出数据中最大的值9,最小值5,故极差是4,
乙中找出数据中最大的值10,最小值2,极差是8,
∴乙成绩变化的幅度大;
(2)从数据中找出成绩相差大的是第一次,相差9﹣2=7环.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
