23.1图形的旋转(2)
文档属性
| 名称 | 23.1图形的旋转(2) |

|
|
| 格式 | rar | ||
| 文件大小 | 440.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-23 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
23.1 图形的旋转(2)
旋转的要素:旋转中心,旋转方向,旋转角度;
1.旋转前、后的图形全等.
4.对应边,对应角相等.
一、旋转的定义:
二、旋转的性质:
2.对应点与旋转中心的距离相等.
3.对应点与旋转中心所连线段的夹角等于旋转角.
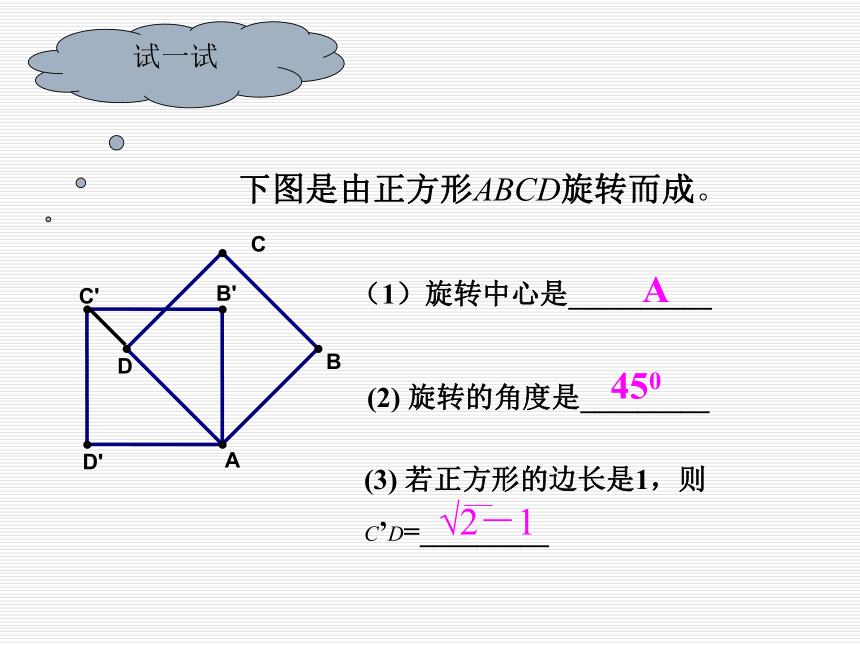
下图是由正方形ABCD旋转而成。
(1)旋转中心是__________
(2) 旋转的角度是_________
试一试
A
450
C
B
C'
D'
B'
A
D
(3) 若正方形的边长是1,则
C’D=_________
√2-1
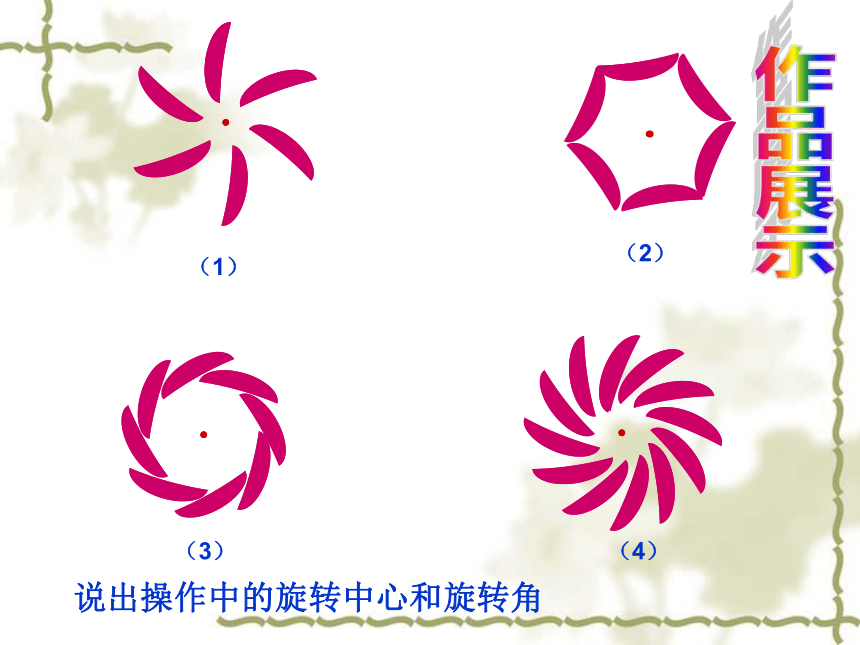
1. 把一个图案(如右图)旋转,选择不同旋转中心以及旋转角,设计出不同的效果图案。
做做看,谁设计的图案美丽。
2. 请设计一个绕一点旋转60°后能与自身重合的图形.
动手操作
说出操作中的旋转中心和旋转角
(1)
(4)
(3)
(2)
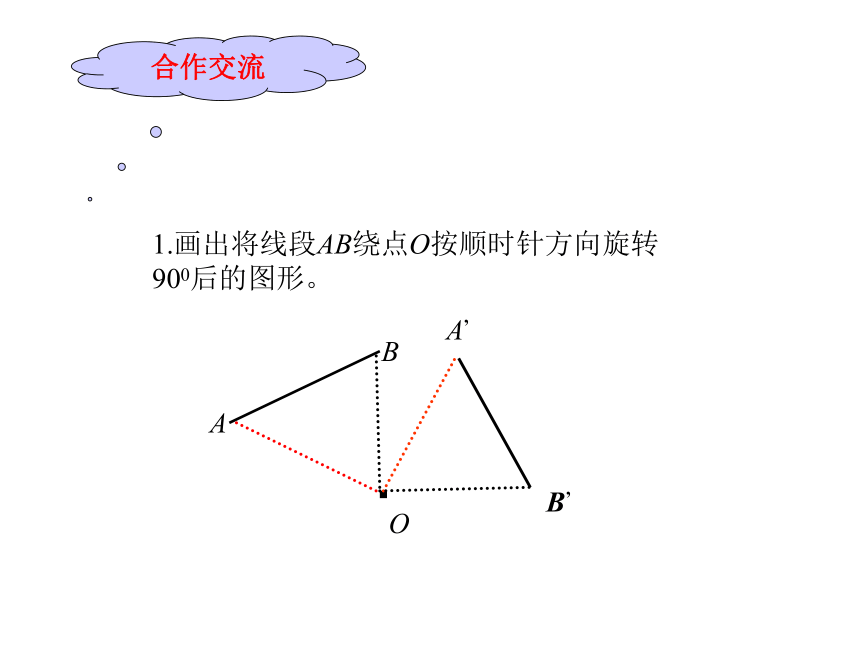
合作交流
1.画出将线段AB绕点O按顺时针方向旋转900后的图形。
O
A
B
A’
B’
合作与交流
2. 画出将△ABC绕点C按逆时针方向旋转900后的对应三角形。
A
B
C
如图: ABC是等边三角形,D是BC上一点, ABD经过 旋转后到达 ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋
转后,点M转到了什么位置?
E
D
C
B
A
M
.
解:(1)旋转中心是A;
(2)旋转了60度;
(3)点M转到了AC的中点位置上.
例题1.
练习1. 如图:P是等边 ABC内的一点,把 ABP按不同的方向通过旋转得到 BQC和 ACR,
(1)指出旋转中心、旋转方向和旋转角度?
(2) ACR是否可以直接通过把 BQC旋转得到?
A
Q
R
P
C
B
⑴如图,画出△ABC绕点A按逆时针方向旋转900后的对应三角形;
例题
D'
B'
D
A
B
C
C'
A
B
C
⑵如果点D是AC的中点,那么经过上述旋转后,点D旋转到什么位置 请在图中将点D的对应点
D′表示出来.
A/
B/
C/
同学们再见!
23.1 图形的旋转(2)
旋转的要素:旋转中心,旋转方向,旋转角度;
1.旋转前、后的图形全等.
4.对应边,对应角相等.
一、旋转的定义:
二、旋转的性质:
2.对应点与旋转中心的距离相等.
3.对应点与旋转中心所连线段的夹角等于旋转角.
下图是由正方形ABCD旋转而成。
(1)旋转中心是__________
(2) 旋转的角度是_________
试一试
A
450
C
B
C'
D'
B'
A
D
(3) 若正方形的边长是1,则
C’D=_________
√2-1
1. 把一个图案(如右图)旋转,选择不同旋转中心以及旋转角,设计出不同的效果图案。
做做看,谁设计的图案美丽。
2. 请设计一个绕一点旋转60°后能与自身重合的图形.
动手操作
说出操作中的旋转中心和旋转角
(1)
(4)
(3)
(2)
合作交流
1.画出将线段AB绕点O按顺时针方向旋转900后的图形。
O
A
B
A’
B’
合作与交流
2. 画出将△ABC绕点C按逆时针方向旋转900后的对应三角形。
A
B
C
如图: ABC是等边三角形,D是BC上一点, ABD经过 旋转后到达 ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋
转后,点M转到了什么位置?
E
D
C
B
A
M
.
解:(1)旋转中心是A;
(2)旋转了60度;
(3)点M转到了AC的中点位置上.
例题1.
练习1. 如图:P是等边 ABC内的一点,把 ABP按不同的方向通过旋转得到 BQC和 ACR,
(1)指出旋转中心、旋转方向和旋转角度?
(2) ACR是否可以直接通过把 BQC旋转得到?
A
Q
R
P
C
B
⑴如图,画出△ABC绕点A按逆时针方向旋转900后的对应三角形;
例题
D'
B'
D
A
B
C
C'
A
B
C
⑵如果点D是AC的中点,那么经过上述旋转后,点D旋转到什么位置 请在图中将点D的对应点
D′表示出来.
A/
B/
C/
同学们再见!
同课章节目录
