2020-2021学年安徽省合肥市瑶海区九年级上学期期中数学试卷 (Word版 含解析)
文档属性
| 名称 | 2020-2021学年安徽省合肥市瑶海区九年级上学期期中数学试卷 (Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 915.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-14 05:53:59 | ||
图片预览


文档简介
2020-2021学年安徽省合肥市瑶海区九年级(上)期中数学试卷
一、选择题(共10小题).
1.(4分)抛物线y=2(x+1)2﹣3的顶点坐标是( )
A.(1,3) B.(﹣1,3) C.(1,﹣3) D.(﹣1,﹣3)
2.(4分)在平面直角坐标系中,抛物线y=(x+5)(x﹣3)经变换后得到抛物线y=(x+3)(x﹣5),则这个变换可以是( )
A.向左平移2个单位 B.向右平移2个单位
C.向左平移8个单位 D.向右平移8个单位
3.(4分)已知点A(1,﹣3)关于y轴的对称点A′在反比例函数y=的图象上,则实数k的值为( )
A.3 B. C.﹣3 D.﹣
4.(4分)已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是( )
A.点火后9s和点火后13s的升空高度相同
B.点火后24s火箭落于地面
C.点火后10s的升空高度为139m
D.火箭升空的最大高度为145m
5.(4分)已知y=x2+(t﹣2)x﹣2,当x>1时y随x的增大而增大,则t的取值范围是( )
A.t>0 B.t=0 C.t<0 D.t≥0
6.(4分)如图,已知D、E分别为AB、AC上的两点,且DE∥BC,AE=3CE,AB=8,则AD的长为( )
A.3 B.4 C.5 D.6
7.(4分)如图,一张矩形纸片ABCD的长AB=a,宽BC=b.将纸片对折,折痕为EF,所得矩形AFED与矩形ABCD相似,则a:b=( )
A.2:1 B.:1 C.3: D.3:2
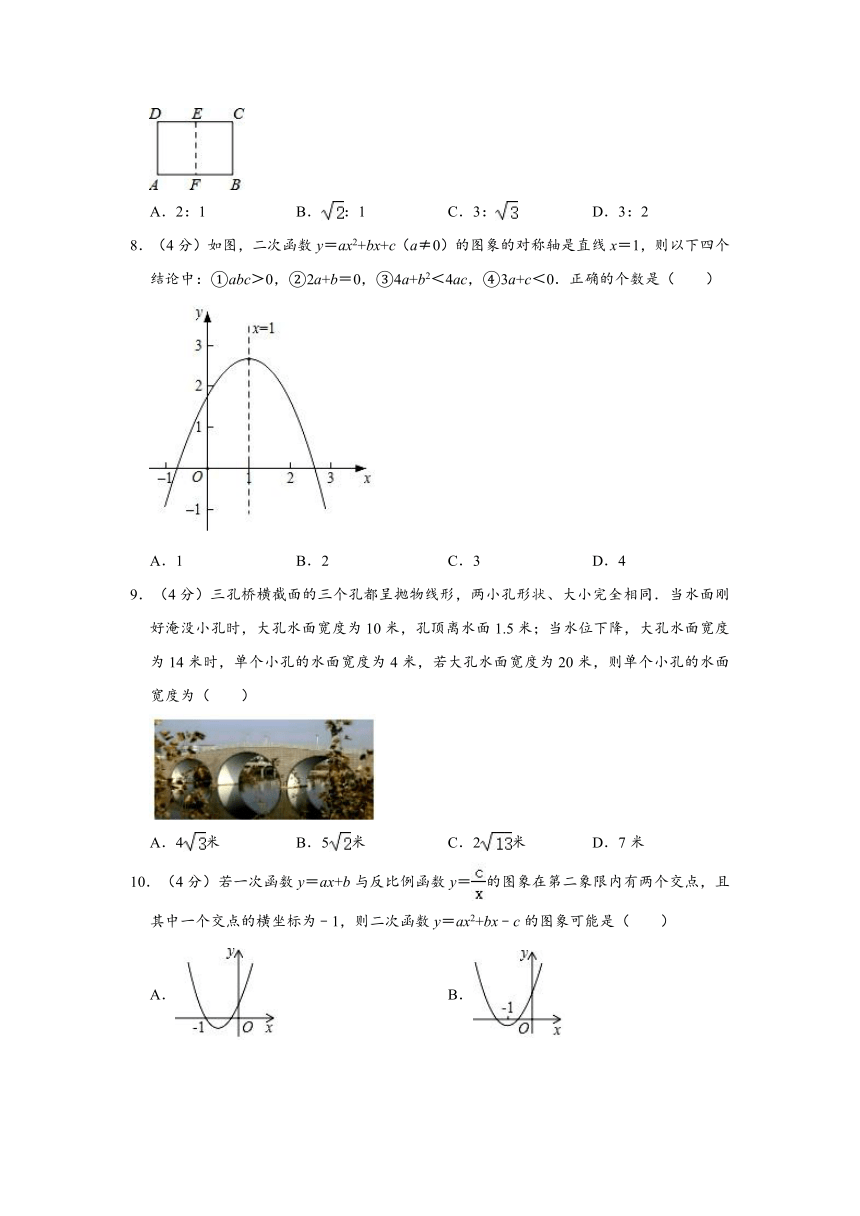
8.(4分)如图,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,则以下四个结论中:①abc>0,②2a+b=0,③4a+b2<4ac,④3a+c<0.正确的个数是( )
A.1 B.2 C.3 D.4
9.(4分)三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( )
A.4米 B.5米 C.2米 D.7米
10.(4分)若一次函数y=ax+b与反比例函数y=的图象在第二象限内有两个交点,且其中一个交点的横坐标为﹣1,则二次函数y=ax2+bx﹣c的图象可能是( )
A. B.
C. D.
二、填空题(每小题5分,满分20分)
11.(5分)若,则= .
12.(5分)已知二次函数y=ax2+bx+c的部分图象如图所示,则关于x的方程ax2+bx+c=0的两个根的和为 .
13.(5分)如图所示,点C在反比例函数y= (x>0)的图象上,过点C的直线与x轴、y轴分别交于点A、B,且AB=BC,已知△AOB的面积为1,则k的值为 .
14.(5分)已知抛物线y=ax2+bx﹣与y轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
(1)此抛物线的对称轴是直线 ;
(2)已知点P(,﹣),Q(2,2),若抛物线与线段PQ恰有一个公共点,则a的取值范围是 .
三、(每小题8分,满分16分)
15.(8分)已知二次函数y=x2+bx+c的图象经过点(4,3)和点(2,﹣1),求该函数的表达式,并求出当0≤x≤3时,y的最值.
16.(8分)已知a:b:c=2:3:4,且a+3b﹣2c=15,求4a﹣3b+c的值.
四、(每小题8分,满分16分)
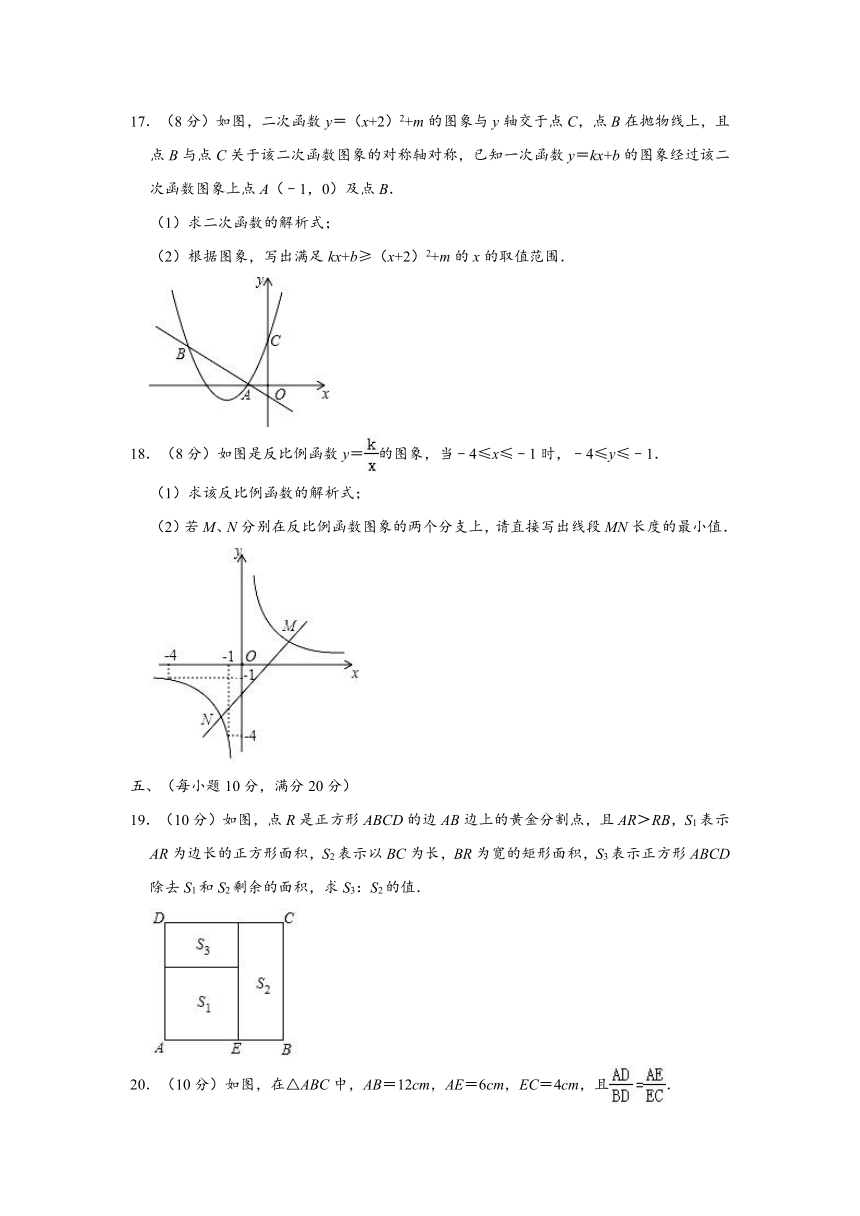
17.(8分)如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且点B与点C关于该二次函数图象的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上点A(﹣1,0)及点B.
(1)求二次函数的解析式;
(2)根据图象,写出满足kx+b≥(x+2)2+m的x的取值范围.
18.(8分)如图是反比例函数y=的图象,当﹣4≤x≤﹣1时,﹣4≤y≤﹣1.
(1)求该反比例函数的解析式;
(2)若M、N分别在反比例函数图象的两个分支上,请直接写出线段MN长度的最小值.
五、(每小题10分,满分20分)
19.(10分)如图,点R是正方形ABCD的边AB边上的黄金分割点,且AR>RB,S1表示AR为边长的正方形面积,S2表示以BC为长,BR为宽的矩形面积,S3表示正方形ABCD除去S1和S2剩余的面积,求S3:S2的值.
20.(10分)如图,在△ABC中,AB=12cm,AE=6cm,EC=4cm,且.
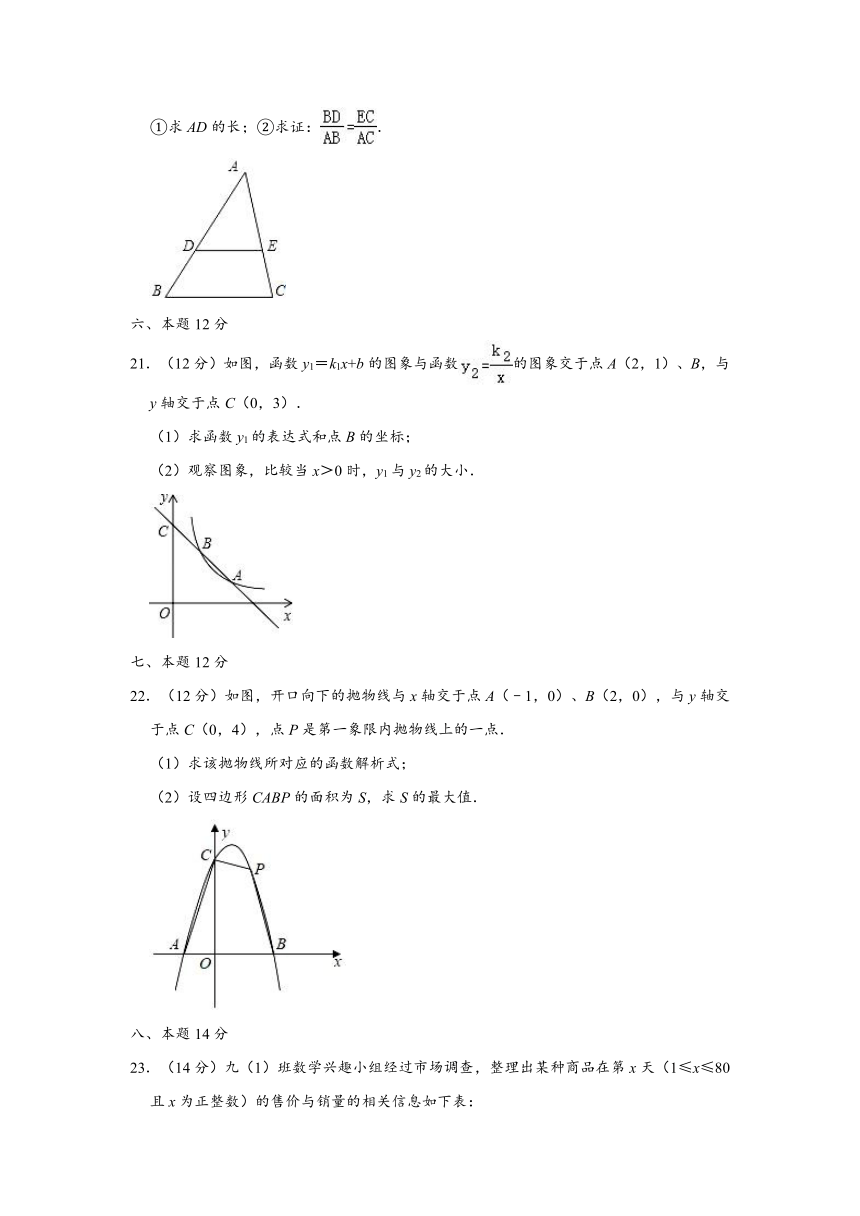
①求AD的长;②求证:.
六、本题12分
21.(12分)如图,函数y1=k1x+b的图象与函数的图象交于点A(2,1)、B,与y轴交于点C(0,3).
(1)求函数y1的表达式和点B的坐标;
(2)观察图象,比较当x>0时,y1与y2的大小.
七、本题12分
22.(12分)如图,开口向下的抛物线与x轴交于点A(﹣1,0)、B(2,0),与y轴交于点C(0,4),点P是第一象限内抛物线上的一点.
(1)求该抛物线所对应的函数解析式;
(2)设四边形CABP的面积为S,求S的最大值.
八、本题14分
23.(14分)九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x天(1≤x≤80且x为正整数)的售价与销量的相关信息如下表:
时间(天) 1≤x≤40 41≤x≤80
售价(元/件) x+40 90
每天销量(件) 200﹣2x 200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800.
参考答案
一、选择题(每小题4分,共10小题,满分40分)
1.(4分)抛物线y=2(x+1)2﹣3的顶点坐标是( )
A.(1,3) B.(﹣1,3) C.(1,﹣3) D.(﹣1,﹣3)
解:∵y=2(x+1)2﹣3是抛物线的顶点式,
根据顶点式的坐标特点可知,顶点坐标为(﹣1,﹣3),
故选:D.
2.(4分)在平面直角坐标系中,抛物线y=(x+5)(x﹣3)经变换后得到抛物线y=(x+3)(x﹣5),则这个变换可以是( )
A.向左平移2个单位 B.向右平移2个单位
C.向左平移8个单位 D.向右平移8个单位
解:y=(x+5)(x﹣3)=(x+1)2﹣16,顶点坐标是(﹣1,﹣16).
y=(x+3)(x﹣5)=(x﹣1)2﹣16,顶点坐标是(1,﹣16).
所以将抛物线y=(x+5)(x﹣3)向右平移2个单位长度得到抛物线y=(x+3)(x﹣5),
故选:B.
3.(4分)已知点A(1,﹣3)关于y轴的对称点A′在反比例函数y=的图象上,则实数k的值为( )
A.3 B. C.﹣3 D.﹣
解:∵点A′与点A(1,﹣3)关于y轴的对称,
∴点A′(﹣1,﹣3),
∵点A′(﹣1,﹣3)在反比例函数y=(k≠0)的图象上,
∴k=(﹣1)×(﹣3)=3,
故选:A.
4.(4分)已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是( )
A.点火后9s和点火后13s的升空高度相同
B.点火后24s火箭落于地面
C.点火后10s的升空高度为139m
D.火箭升空的最大高度为145m
解:A、当t=9时,h=136;当t=13时,h=144;所以点火后9s和点火后13s的升空高度不相同,此选项错误;
B、当t=24时h=1≠0,所以点火后24s火箭离地面的高度为1m,此选项错误;
C、当t=10时h=141m,此选项错误;
D、由h=﹣t2+24t+1=﹣(t﹣12)2+145知火箭升空的最大高度为145m,此选项正确;
故选:D.
5.(4分)已知y=x2+(t﹣2)x﹣2,当x>1时y随x的增大而增大,则t的取值范围是( )
A.t>0 B.t=0 C.t<0 D.t≥0
解:
∵y=x2+(t﹣2)x﹣2,
∴抛物线对称轴为x=﹣,开口向上,
∴在对称轴右侧y随x的增大而增大,
∵当x>1时y随x的增大而增大,
∴﹣≤1,解得t≥0,
故选:D.
6.(4分)如图,已知D、E分别为AB、AC上的两点,且DE∥BC,AE=3CE,AB=8,则AD的长为( )
A.3 B.4 C.5 D.6
解:∵DE∥BC,
∴===,
∴AD=×8=6.
故选:D.
7.(4分)如图,一张矩形纸片ABCD的长AB=a,宽BC=b.将纸片对折,折痕为EF,所得矩形AFED与矩形ABCD相似,则a:b=( )
A.2:1 B.:1 C.3: D.3:2
解:∵矩形纸片对折,折痕为EF,
∴AF=AB=a,
∵矩形AFED与矩形ABCD相似,
∴=,即=,
∴()2=2,
∴=.
故选:B.
8.(4分)如图,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,则以下四个结论中:①abc>0,②2a+b=0,③4a+b2<4ac,④3a+c<0.正确的个数是( )
A.1 B.2 C.3 D.4
解:①根据抛物线开口向下可知:
a<0,
因为对称轴在y轴右侧,
所以b>0,
因为抛物线与y轴正半轴相交,
所以c>0,
所以abc<0,
所以①错误;
②因为抛物线对称轴是直线x=1,
即﹣=1,
所以b=﹣2a,
所以b+2a=0,
所以②正确;
③因为b=﹣2a,
由4a+b2<4ac,得
4a+4a2<4ac,
∵a<0,
∴c<1+a,
根据抛物线与y轴的交点,c>1,
所以③错误;
④当x=﹣1时,y<0,
即a﹣b+c<0,
因为b=﹣2a,
所以3a+c<0,
所以④正确.
所以正确的是②④2个.
故选:B.
9.(4分)三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( )
A.4米 B.5米 C.2米 D.7米
解:如图,建立如图所示的平面直角坐标系,由题意可得MN=4,EF=14,BC=10,DO=,
设大孔所在抛物线解析式为y=ax2+,
∵BC=10,
∴点B(﹣5,0),
∴0=a×(﹣5)2+,
∴a=﹣,
∴大孔所在抛物线解析式为y=﹣x2+,
设点A(b,0),则设顶点为A的小孔所在抛物线的解析式为y=m(x﹣b)2,
∵EF=14,
∴点E的横坐标为﹣7,
∴点E坐标为(﹣7,﹣),
∴﹣=m(x﹣b)2,
∴x1=+b,x2=﹣+b,
∴MN=4,
∴|+b﹣(﹣+b)|=4
∴m=﹣,
∴顶点为A的小孔所在抛物线的解析式为y=﹣(x﹣b)2,
∵大孔水面宽度为20米,
∴当x=﹣10时,y=﹣,
∴﹣=﹣(x﹣b)2,
∴x1=+b,x2=﹣+b,
∴单个小孔的水面宽度=|(+b)﹣(﹣+b)|=5(米),
故选:B.
10.(4分)若一次函数y=ax+b与反比例函数y=的图象在第二象限内有两个交点,且其中一个交点的横坐标为﹣1,则二次函数y=ax2+bx﹣c的图象可能是( )
A. B.
C. D.
解:∵直线y=ax+b与反比例函数y=的图象在第二象限内有一个交点的横坐标为﹣1,
∴﹣c=﹣a+b,
∴a﹣b﹣c=0,
∵一次函数y=ax+b与反比例函数y=的图象在第二象限内有两个交点,
∴a>0,
∴二次函数y=ax2+bx﹣c的图象开口向上,
当x=﹣1时,y=a﹣b﹣c=0,
∴抛物线y=ax2+bx﹣c过(﹣1,0)点,
故选:A.
二、填空题(每小题5分,满分20分)
11.(5分)若,则= .
解:∵,
∴==,
12.(5分)已知二次函数y=ax2+bx+c的部分图象如图所示,则关于x的方程ax2+bx+c=0的两个根的和为 2 .
解:∵二次函数y=ax2+bx+c的对称轴为x=1,
∴﹣=1,
∴b=﹣2a,
∴关于x的方程ax2+bx+c=0的两个根的和为﹣=2.
故答案为:2.
13.(5分)如图所示,点C在反比例函数y= (x>0)的图象上,过点C的直线与x轴、y轴分别交于点A、B,且AB=BC,已知△AOB的面积为1,则k的值为 4 .
解:设点A的坐标为(﹣a,0),
∵过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,
∴点C(a,),
∴点B的坐标为(0,),
∴=1,
解得,k=4,
故答案为:4.
14.(5分)已知抛物线y=ax2+bx﹣与y轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
(1)此抛物线的对称轴是直线 x=1 ;
(2)已知点P(,﹣),Q(2,2),若抛物线与线段PQ恰有一个公共点,则a的取值范围是 a≤﹣ .
解:(1)∵抛物线y=ax2+bx﹣与y轴交于点A,
∴A(0,﹣)
∴点A向右平移2个单位长度,得到点B(2,﹣),
∵点B也在抛物线上,
∴A、B关于对称轴对称,
∴抛物线对称轴为直线x==1;
(2)∵对称轴x=1,
∴b=﹣2a,
∴y=ax2﹣2ax﹣,
①a>0时,
当x=2时,y=﹣<2,
当y=﹣时,x=0或x=2,
∴函数与PQ无交点;
②a<0时,
当y=2时,ax2﹣2ax﹣=2,
解得,x=或x=,
当≤2时,a≤﹣;
∴当a≤﹣时,抛物线与线段PQ恰有一个公共点,
故答案为a≤﹣.
三、(每小题8分,满分16分)
15.(8分)已知二次函数y=x2+bx+c的图象经过点(4,3)和点(2,﹣1),求该函数的表达式,并求出当0≤x≤3时,y的最值.
解:∵二次函数y=x2+bx+c的图象经过点(4,3),(2,﹣1),
∴,
解得,,
∴函数解析式为:y=x2﹣4x+3,
y=x2﹣4x+3=(x﹣2)2﹣1,
∴当x=0时,y=3,当x=3时,y=0,
y的最值是﹣1≤y≤3,.
16.(8分)已知a:b:c=2:3:4,且a+3b﹣2c=15,求4a﹣3b+c的值.
解:由题意设a=2k,b=3k,c=4k,
∵a+3b﹣2c=15,
∴2k+9k﹣8k=15,
∴k=5,
∴a=10,b=15,c=20;
∴4a﹣3b+c
=4×10﹣3×15+20
=15.
四、(每小题8分,满分16分)
17.(8分)如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且点B与点C关于该二次函数图象的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上点A(﹣1,0)及点B.
(1)求二次函数的解析式;
(2)根据图象,写出满足kx+b≥(x+2)2+m的x的取值范围.
解:(1)∵抛物线y=(x+2)2+m经过点A(﹣1,0),
∴0=1+m,
∴m=﹣1,
∴抛物线解析式为y=(x+2)2﹣1;
(2)令x=0,则y=(x+2)2﹣1=3,
∴点C坐标(0,3),
∵对称轴为直线x=﹣2,B、C关于对称轴对称,
∴点B坐标(﹣4,3),
由图象可知,满足kx+b≥(x+2)2+m的x的取值范围为﹣4≤x≤﹣1.
18.(8分)如图是反比例函数y=的图象,当﹣4≤x≤﹣1时,﹣4≤y≤﹣1.
(1)求该反比例函数的解析式;
(2)若M、N分别在反比例函数图象的两个分支上,请直接写出线段MN长度的最小值.
解:(1)∵在反比例函数的图象中,当﹣4≤x≤﹣1时,﹣4≤y≤﹣1,
∴反比例函数经过坐标(﹣4,﹣1),
∴﹣4=,
∴k=4,
∴反比例函数的解析式为y=;
(2)当M,N为一,三象限角平分线与反比例函数图象的交点时,线段MN最短.
将y=x代入y=,
解得或,
即M(2,2),N(﹣2,﹣2).
∴OM=2.
则MN=4.
∴线段MN的最小值为4.
五、(每小题10分,满分20分)
19.(10分)如图,点R是正方形ABCD的边AB边上的黄金分割点,且AR>RB,S1表示AR为边长的正方形面积,S2表示以BC为长,BR为宽的矩形面积,S3表示正方形ABCD除去S1和S2剩余的面积,求S3:S2的值.
解:如图,设AB=1,
∵点E是正方形ABCD的边AB边上的黄金分割点,且AE>EB,
∴AE=GF=,
∴BE=FH=AB﹣AE=,
∴S3:S2=(GF?FH):(BC?BE)
=(×):(1×)
=.
故答案为:.
20.(10分)如图,在△ABC中,AB=12cm,AE=6cm,EC=4cm,且.
①求AD的长;②求证:.
解:①设AD=xcm,则BD=AB﹣AD=(12﹣x)cm
∵,
∴
解得x=7.2cm
∴AD=7.2cm;
②∵,
∴
即.
∴.
六、本题12分
21.(12分)如图,函数y1=k1x+b的图象与函数的图象交于点A(2,1)、B,与y轴交于点C(0,3).
(1)求函数y1的表达式和点B的坐标;
(2)观察图象,比较当x>0时,y1与y2的大小.
解:(1)∵函数y1=k1x+b的图象与函数的图象交于点A(2,1),
∴=1,
解得k2=2,
∴反比例函数解析式为y2=,
∵函数y1=k1x+b经过点A(2,1),C(0,3),
∴,
解得,
∴y1=﹣x+3,
两解析式联立得,,
解得,
∴点B的坐标为B(1,2);
(2)根据图象,当0<x<1或x>2时,y1<y2,当1<x<2时,y1>y2,当x=1或x=2时,y1=y2.
七、本题12分
22.(12分)如图,开口向下的抛物线与x轴交于点A(﹣1,0)、B(2,0),与y轴交于点C(0,4),点P是第一象限内抛物线上的一点.
(1)求该抛物线所对应的函数解析式;
(2)设四边形CABP的面积为S,求S的最大值.
解:(1)∵A(﹣1,0),B(2,0),C(0,4),
设抛物线表达式为:y=a(x+1)(x﹣2),
将C代入得:4=﹣2a,
解得:a=﹣2,
∴该抛物线的解析式为:y=﹣2(x+1)(x﹣2)=﹣2x2+2x+4;
(2)连接OP,设点P坐标为(m,﹣2m2+2m+4),m>0,
∵A(﹣1,0),B(2,0),C(0,4),
可得:OA=1,OC=4,OB=2,
∴S=S四边形CABP=S△OAC+S△OCP+S△OPB
=×1×4+×4m+×2×(﹣2m2+2m+4)
=﹣2m2+4m+6
=﹣2(m﹣1)2+8,
当m=1时,S最大,最大值为8.
八、本题14分
23.(14分)九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x天(1≤x≤80且x为正整数)的售价与销量的相关信息如下表:
时间(天) 1≤x≤40 41≤x≤80
售价(元/件) x+40 90
每天销量(件) 200﹣2x 200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800.
解:(1)由题意得:y=(200﹣2x)(x+40﹣30)或y=(200﹣2x)(90﹣30),
(2)当1≤x≤40时,y=﹣2(x+10)(x﹣100),则函数对称轴为x=45,
故x=40时,函数取得最大值为6000,
当41≤x≤80时,y=12000﹣120x,函数在x=41时,取得最大值为:7080,
故:第41天,利润最大,最大利润为7080元;
(3)当1≤x≤40时,y=﹣2(x+10)(x﹣100)≥4800,
解得:20≤x≤70,20≤x≤40,为21天,
则函数对称轴为x=45,故x=40时,函数取得最大值为4000,
当41≤x≤80时,y=12000﹣120x≥4800,x≤60,即:41≤x≤60,为20天,
故:共有41天.
一、选择题(共10小题).
1.(4分)抛物线y=2(x+1)2﹣3的顶点坐标是( )
A.(1,3) B.(﹣1,3) C.(1,﹣3) D.(﹣1,﹣3)
2.(4分)在平面直角坐标系中,抛物线y=(x+5)(x﹣3)经变换后得到抛物线y=(x+3)(x﹣5),则这个变换可以是( )
A.向左平移2个单位 B.向右平移2个单位
C.向左平移8个单位 D.向右平移8个单位
3.(4分)已知点A(1,﹣3)关于y轴的对称点A′在反比例函数y=的图象上,则实数k的值为( )
A.3 B. C.﹣3 D.﹣
4.(4分)已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是( )
A.点火后9s和点火后13s的升空高度相同
B.点火后24s火箭落于地面
C.点火后10s的升空高度为139m
D.火箭升空的最大高度为145m
5.(4分)已知y=x2+(t﹣2)x﹣2,当x>1时y随x的增大而增大,则t的取值范围是( )
A.t>0 B.t=0 C.t<0 D.t≥0
6.(4分)如图,已知D、E分别为AB、AC上的两点,且DE∥BC,AE=3CE,AB=8,则AD的长为( )
A.3 B.4 C.5 D.6
7.(4分)如图,一张矩形纸片ABCD的长AB=a,宽BC=b.将纸片对折,折痕为EF,所得矩形AFED与矩形ABCD相似,则a:b=( )
A.2:1 B.:1 C.3: D.3:2
8.(4分)如图,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,则以下四个结论中:①abc>0,②2a+b=0,③4a+b2<4ac,④3a+c<0.正确的个数是( )
A.1 B.2 C.3 D.4
9.(4分)三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( )
A.4米 B.5米 C.2米 D.7米
10.(4分)若一次函数y=ax+b与反比例函数y=的图象在第二象限内有两个交点,且其中一个交点的横坐标为﹣1,则二次函数y=ax2+bx﹣c的图象可能是( )
A. B.
C. D.
二、填空题(每小题5分,满分20分)
11.(5分)若,则= .
12.(5分)已知二次函数y=ax2+bx+c的部分图象如图所示,则关于x的方程ax2+bx+c=0的两个根的和为 .
13.(5分)如图所示,点C在反比例函数y= (x>0)的图象上,过点C的直线与x轴、y轴分别交于点A、B,且AB=BC,已知△AOB的面积为1,则k的值为 .
14.(5分)已知抛物线y=ax2+bx﹣与y轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
(1)此抛物线的对称轴是直线 ;
(2)已知点P(,﹣),Q(2,2),若抛物线与线段PQ恰有一个公共点,则a的取值范围是 .
三、(每小题8分,满分16分)
15.(8分)已知二次函数y=x2+bx+c的图象经过点(4,3)和点(2,﹣1),求该函数的表达式,并求出当0≤x≤3时,y的最值.
16.(8分)已知a:b:c=2:3:4,且a+3b﹣2c=15,求4a﹣3b+c的值.
四、(每小题8分,满分16分)
17.(8分)如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且点B与点C关于该二次函数图象的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上点A(﹣1,0)及点B.
(1)求二次函数的解析式;
(2)根据图象,写出满足kx+b≥(x+2)2+m的x的取值范围.
18.(8分)如图是反比例函数y=的图象,当﹣4≤x≤﹣1时,﹣4≤y≤﹣1.
(1)求该反比例函数的解析式;
(2)若M、N分别在反比例函数图象的两个分支上,请直接写出线段MN长度的最小值.
五、(每小题10分,满分20分)
19.(10分)如图,点R是正方形ABCD的边AB边上的黄金分割点,且AR>RB,S1表示AR为边长的正方形面积,S2表示以BC为长,BR为宽的矩形面积,S3表示正方形ABCD除去S1和S2剩余的面积,求S3:S2的值.
20.(10分)如图,在△ABC中,AB=12cm,AE=6cm,EC=4cm,且.
①求AD的长;②求证:.
六、本题12分
21.(12分)如图,函数y1=k1x+b的图象与函数的图象交于点A(2,1)、B,与y轴交于点C(0,3).
(1)求函数y1的表达式和点B的坐标;
(2)观察图象,比较当x>0时,y1与y2的大小.
七、本题12分
22.(12分)如图,开口向下的抛物线与x轴交于点A(﹣1,0)、B(2,0),与y轴交于点C(0,4),点P是第一象限内抛物线上的一点.
(1)求该抛物线所对应的函数解析式;
(2)设四边形CABP的面积为S,求S的最大值.
八、本题14分
23.(14分)九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x天(1≤x≤80且x为正整数)的售价与销量的相关信息如下表:
时间(天) 1≤x≤40 41≤x≤80
售价(元/件) x+40 90
每天销量(件) 200﹣2x 200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800.
参考答案
一、选择题(每小题4分,共10小题,满分40分)
1.(4分)抛物线y=2(x+1)2﹣3的顶点坐标是( )
A.(1,3) B.(﹣1,3) C.(1,﹣3) D.(﹣1,﹣3)
解:∵y=2(x+1)2﹣3是抛物线的顶点式,
根据顶点式的坐标特点可知,顶点坐标为(﹣1,﹣3),
故选:D.
2.(4分)在平面直角坐标系中,抛物线y=(x+5)(x﹣3)经变换后得到抛物线y=(x+3)(x﹣5),则这个变换可以是( )
A.向左平移2个单位 B.向右平移2个单位
C.向左平移8个单位 D.向右平移8个单位
解:y=(x+5)(x﹣3)=(x+1)2﹣16,顶点坐标是(﹣1,﹣16).
y=(x+3)(x﹣5)=(x﹣1)2﹣16,顶点坐标是(1,﹣16).
所以将抛物线y=(x+5)(x﹣3)向右平移2个单位长度得到抛物线y=(x+3)(x﹣5),
故选:B.
3.(4分)已知点A(1,﹣3)关于y轴的对称点A′在反比例函数y=的图象上,则实数k的值为( )
A.3 B. C.﹣3 D.﹣
解:∵点A′与点A(1,﹣3)关于y轴的对称,
∴点A′(﹣1,﹣3),
∵点A′(﹣1,﹣3)在反比例函数y=(k≠0)的图象上,
∴k=(﹣1)×(﹣3)=3,
故选:A.
4.(4分)已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是( )
A.点火后9s和点火后13s的升空高度相同
B.点火后24s火箭落于地面
C.点火后10s的升空高度为139m
D.火箭升空的最大高度为145m
解:A、当t=9时,h=136;当t=13时,h=144;所以点火后9s和点火后13s的升空高度不相同,此选项错误;
B、当t=24时h=1≠0,所以点火后24s火箭离地面的高度为1m,此选项错误;
C、当t=10时h=141m,此选项错误;
D、由h=﹣t2+24t+1=﹣(t﹣12)2+145知火箭升空的最大高度为145m,此选项正确;
故选:D.
5.(4分)已知y=x2+(t﹣2)x﹣2,当x>1时y随x的增大而增大,则t的取值范围是( )
A.t>0 B.t=0 C.t<0 D.t≥0
解:
∵y=x2+(t﹣2)x﹣2,
∴抛物线对称轴为x=﹣,开口向上,
∴在对称轴右侧y随x的增大而增大,
∵当x>1时y随x的增大而增大,
∴﹣≤1,解得t≥0,
故选:D.
6.(4分)如图,已知D、E分别为AB、AC上的两点,且DE∥BC,AE=3CE,AB=8,则AD的长为( )
A.3 B.4 C.5 D.6
解:∵DE∥BC,
∴===,
∴AD=×8=6.
故选:D.
7.(4分)如图,一张矩形纸片ABCD的长AB=a,宽BC=b.将纸片对折,折痕为EF,所得矩形AFED与矩形ABCD相似,则a:b=( )
A.2:1 B.:1 C.3: D.3:2
解:∵矩形纸片对折,折痕为EF,
∴AF=AB=a,
∵矩形AFED与矩形ABCD相似,
∴=,即=,
∴()2=2,
∴=.
故选:B.
8.(4分)如图,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,则以下四个结论中:①abc>0,②2a+b=0,③4a+b2<4ac,④3a+c<0.正确的个数是( )
A.1 B.2 C.3 D.4
解:①根据抛物线开口向下可知:
a<0,
因为对称轴在y轴右侧,
所以b>0,
因为抛物线与y轴正半轴相交,
所以c>0,
所以abc<0,
所以①错误;
②因为抛物线对称轴是直线x=1,
即﹣=1,
所以b=﹣2a,
所以b+2a=0,
所以②正确;
③因为b=﹣2a,
由4a+b2<4ac,得
4a+4a2<4ac,
∵a<0,
∴c<1+a,
根据抛物线与y轴的交点,c>1,
所以③错误;
④当x=﹣1时,y<0,
即a﹣b+c<0,
因为b=﹣2a,
所以3a+c<0,
所以④正确.
所以正确的是②④2个.
故选:B.
9.(4分)三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( )
A.4米 B.5米 C.2米 D.7米
解:如图,建立如图所示的平面直角坐标系,由题意可得MN=4,EF=14,BC=10,DO=,
设大孔所在抛物线解析式为y=ax2+,
∵BC=10,
∴点B(﹣5,0),
∴0=a×(﹣5)2+,
∴a=﹣,
∴大孔所在抛物线解析式为y=﹣x2+,
设点A(b,0),则设顶点为A的小孔所在抛物线的解析式为y=m(x﹣b)2,
∵EF=14,
∴点E的横坐标为﹣7,
∴点E坐标为(﹣7,﹣),
∴﹣=m(x﹣b)2,
∴x1=+b,x2=﹣+b,
∴MN=4,
∴|+b﹣(﹣+b)|=4
∴m=﹣,
∴顶点为A的小孔所在抛物线的解析式为y=﹣(x﹣b)2,
∵大孔水面宽度为20米,
∴当x=﹣10时,y=﹣,
∴﹣=﹣(x﹣b)2,
∴x1=+b,x2=﹣+b,
∴单个小孔的水面宽度=|(+b)﹣(﹣+b)|=5(米),
故选:B.
10.(4分)若一次函数y=ax+b与反比例函数y=的图象在第二象限内有两个交点,且其中一个交点的横坐标为﹣1,则二次函数y=ax2+bx﹣c的图象可能是( )
A. B.
C. D.
解:∵直线y=ax+b与反比例函数y=的图象在第二象限内有一个交点的横坐标为﹣1,
∴﹣c=﹣a+b,
∴a﹣b﹣c=0,
∵一次函数y=ax+b与反比例函数y=的图象在第二象限内有两个交点,
∴a>0,
∴二次函数y=ax2+bx﹣c的图象开口向上,
当x=﹣1时,y=a﹣b﹣c=0,
∴抛物线y=ax2+bx﹣c过(﹣1,0)点,
故选:A.
二、填空题(每小题5分,满分20分)
11.(5分)若,则= .
解:∵,
∴==,
12.(5分)已知二次函数y=ax2+bx+c的部分图象如图所示,则关于x的方程ax2+bx+c=0的两个根的和为 2 .
解:∵二次函数y=ax2+bx+c的对称轴为x=1,
∴﹣=1,
∴b=﹣2a,
∴关于x的方程ax2+bx+c=0的两个根的和为﹣=2.
故答案为:2.
13.(5分)如图所示,点C在反比例函数y= (x>0)的图象上,过点C的直线与x轴、y轴分别交于点A、B,且AB=BC,已知△AOB的面积为1,则k的值为 4 .
解:设点A的坐标为(﹣a,0),
∵过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,
∴点C(a,),
∴点B的坐标为(0,),
∴=1,
解得,k=4,
故答案为:4.
14.(5分)已知抛物线y=ax2+bx﹣与y轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
(1)此抛物线的对称轴是直线 x=1 ;
(2)已知点P(,﹣),Q(2,2),若抛物线与线段PQ恰有一个公共点,则a的取值范围是 a≤﹣ .
解:(1)∵抛物线y=ax2+bx﹣与y轴交于点A,
∴A(0,﹣)
∴点A向右平移2个单位长度,得到点B(2,﹣),
∵点B也在抛物线上,
∴A、B关于对称轴对称,
∴抛物线对称轴为直线x==1;
(2)∵对称轴x=1,
∴b=﹣2a,
∴y=ax2﹣2ax﹣,
①a>0时,
当x=2时,y=﹣<2,
当y=﹣时,x=0或x=2,
∴函数与PQ无交点;
②a<0时,
当y=2时,ax2﹣2ax﹣=2,
解得,x=或x=,
当≤2时,a≤﹣;
∴当a≤﹣时,抛物线与线段PQ恰有一个公共点,
故答案为a≤﹣.
三、(每小题8分,满分16分)
15.(8分)已知二次函数y=x2+bx+c的图象经过点(4,3)和点(2,﹣1),求该函数的表达式,并求出当0≤x≤3时,y的最值.
解:∵二次函数y=x2+bx+c的图象经过点(4,3),(2,﹣1),
∴,
解得,,
∴函数解析式为:y=x2﹣4x+3,
y=x2﹣4x+3=(x﹣2)2﹣1,
∴当x=0时,y=3,当x=3时,y=0,
y的最值是﹣1≤y≤3,.
16.(8分)已知a:b:c=2:3:4,且a+3b﹣2c=15,求4a﹣3b+c的值.
解:由题意设a=2k,b=3k,c=4k,
∵a+3b﹣2c=15,
∴2k+9k﹣8k=15,
∴k=5,
∴a=10,b=15,c=20;
∴4a﹣3b+c
=4×10﹣3×15+20
=15.
四、(每小题8分,满分16分)
17.(8分)如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且点B与点C关于该二次函数图象的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上点A(﹣1,0)及点B.
(1)求二次函数的解析式;
(2)根据图象,写出满足kx+b≥(x+2)2+m的x的取值范围.
解:(1)∵抛物线y=(x+2)2+m经过点A(﹣1,0),
∴0=1+m,
∴m=﹣1,
∴抛物线解析式为y=(x+2)2﹣1;
(2)令x=0,则y=(x+2)2﹣1=3,
∴点C坐标(0,3),
∵对称轴为直线x=﹣2,B、C关于对称轴对称,
∴点B坐标(﹣4,3),
由图象可知,满足kx+b≥(x+2)2+m的x的取值范围为﹣4≤x≤﹣1.
18.(8分)如图是反比例函数y=的图象,当﹣4≤x≤﹣1时,﹣4≤y≤﹣1.
(1)求该反比例函数的解析式;
(2)若M、N分别在反比例函数图象的两个分支上,请直接写出线段MN长度的最小值.
解:(1)∵在反比例函数的图象中,当﹣4≤x≤﹣1时,﹣4≤y≤﹣1,
∴反比例函数经过坐标(﹣4,﹣1),
∴﹣4=,
∴k=4,
∴反比例函数的解析式为y=;
(2)当M,N为一,三象限角平分线与反比例函数图象的交点时,线段MN最短.
将y=x代入y=,
解得或,
即M(2,2),N(﹣2,﹣2).
∴OM=2.
则MN=4.
∴线段MN的最小值为4.
五、(每小题10分,满分20分)
19.(10分)如图,点R是正方形ABCD的边AB边上的黄金分割点,且AR>RB,S1表示AR为边长的正方形面积,S2表示以BC为长,BR为宽的矩形面积,S3表示正方形ABCD除去S1和S2剩余的面积,求S3:S2的值.
解:如图,设AB=1,
∵点E是正方形ABCD的边AB边上的黄金分割点,且AE>EB,
∴AE=GF=,
∴BE=FH=AB﹣AE=,
∴S3:S2=(GF?FH):(BC?BE)
=(×):(1×)
=.
故答案为:.
20.(10分)如图,在△ABC中,AB=12cm,AE=6cm,EC=4cm,且.
①求AD的长;②求证:.
解:①设AD=xcm,则BD=AB﹣AD=(12﹣x)cm
∵,
∴
解得x=7.2cm
∴AD=7.2cm;
②∵,
∴
即.
∴.
六、本题12分
21.(12分)如图,函数y1=k1x+b的图象与函数的图象交于点A(2,1)、B,与y轴交于点C(0,3).
(1)求函数y1的表达式和点B的坐标;
(2)观察图象,比较当x>0时,y1与y2的大小.
解:(1)∵函数y1=k1x+b的图象与函数的图象交于点A(2,1),
∴=1,
解得k2=2,
∴反比例函数解析式为y2=,
∵函数y1=k1x+b经过点A(2,1),C(0,3),
∴,
解得,
∴y1=﹣x+3,
两解析式联立得,,
解得,
∴点B的坐标为B(1,2);
(2)根据图象,当0<x<1或x>2时,y1<y2,当1<x<2时,y1>y2,当x=1或x=2时,y1=y2.
七、本题12分
22.(12分)如图,开口向下的抛物线与x轴交于点A(﹣1,0)、B(2,0),与y轴交于点C(0,4),点P是第一象限内抛物线上的一点.
(1)求该抛物线所对应的函数解析式;
(2)设四边形CABP的面积为S,求S的最大值.
解:(1)∵A(﹣1,0),B(2,0),C(0,4),
设抛物线表达式为:y=a(x+1)(x﹣2),
将C代入得:4=﹣2a,
解得:a=﹣2,
∴该抛物线的解析式为:y=﹣2(x+1)(x﹣2)=﹣2x2+2x+4;
(2)连接OP,设点P坐标为(m,﹣2m2+2m+4),m>0,
∵A(﹣1,0),B(2,0),C(0,4),
可得:OA=1,OC=4,OB=2,
∴S=S四边形CABP=S△OAC+S△OCP+S△OPB
=×1×4+×4m+×2×(﹣2m2+2m+4)
=﹣2m2+4m+6
=﹣2(m﹣1)2+8,
当m=1时,S最大,最大值为8.
八、本题14分
23.(14分)九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x天(1≤x≤80且x为正整数)的售价与销量的相关信息如下表:
时间(天) 1≤x≤40 41≤x≤80
售价(元/件) x+40 90
每天销量(件) 200﹣2x 200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800.
解:(1)由题意得:y=(200﹣2x)(x+40﹣30)或y=(200﹣2x)(90﹣30),
(2)当1≤x≤40时,y=﹣2(x+10)(x﹣100),则函数对称轴为x=45,
故x=40时,函数取得最大值为6000,
当41≤x≤80时,y=12000﹣120x,函数在x=41时,取得最大值为:7080,
故:第41天,利润最大,最大利润为7080元;
(3)当1≤x≤40时,y=﹣2(x+10)(x﹣100)≥4800,
解得:20≤x≤70,20≤x≤40,为21天,
则函数对称轴为x=45,故x=40时,函数取得最大值为4000,
当41≤x≤80时,y=12000﹣120x≥4800,x≤60,即:41≤x≤60,为20天,
故:共有41天.
同课章节目录
