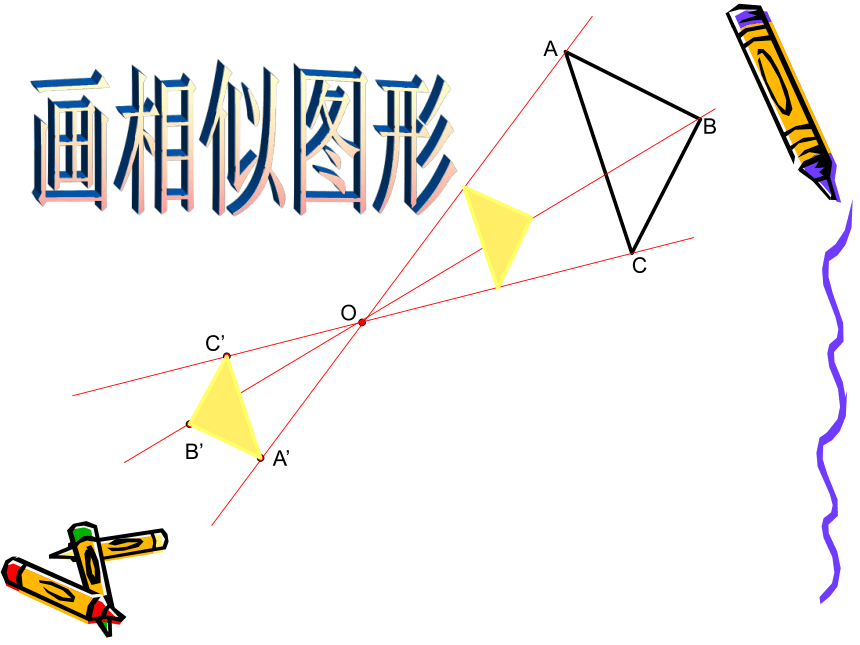
24.5画相似图形
图片预览



文档简介
(共30张PPT)
A
B
A’
C’
B’
C
O
前面我们已经学习了图形的哪些变换?
平移:平移的方向,平移的距离.
旋转:旋转中心,旋转方向,旋转角度.
相似:相似比.
对称(轴对称与轴对称图形,中心对称与中心对称图形):对称轴,对称中心.
相似与轴对称,平移,旋转一样,也是图形之间的一个基本变换.可以将一个图形放大或缩小,保持形状不变,得到它的相似图形.
如何便捷的画出一个图形的相似图形呢
这节课我们学习画相似图形的一种特殊方法
下面请欣赏如下图形的变换
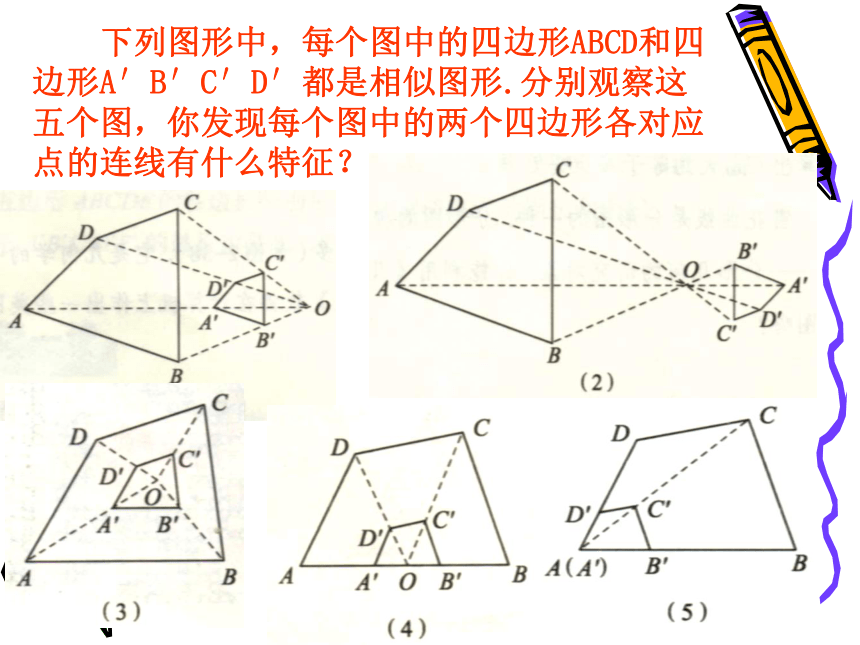
下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对应点的连线有什么特征?
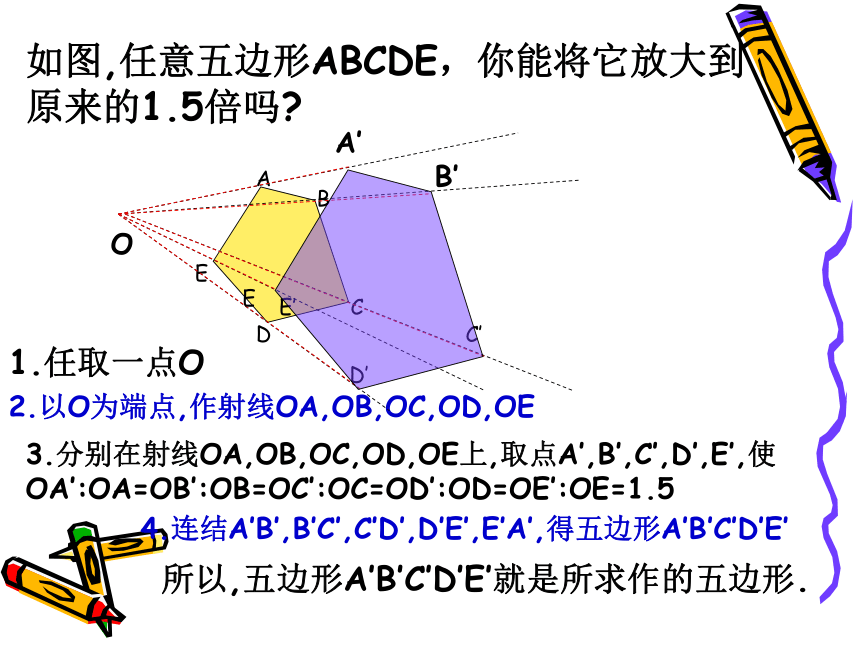
如图,任意五边形ABCDE,你能将它放大到原来的1.5倍吗
A
B
C
E
D
1.任取一点O
O
2.以O为端点,作射线OA,OB,OC,OD,OE
3.分别在射线OA,OB,OC,OD,OE上,取点A’,B’,C’,D’,E’,使 OA’:OA=OB’:OB=OC’:OC=OD’:OD=OE’:OE=1.5
A’
B’
C’
D’
E’
4.连结A’B’,B’C’,C’D’,D’E’,E’A’,得五边形A’B’C’D’E’
E
所以,五边形A’B’C’D’E’就是所求作的五边形.
A
B
C
E
D
O
A’
B’
C’
D’
E’
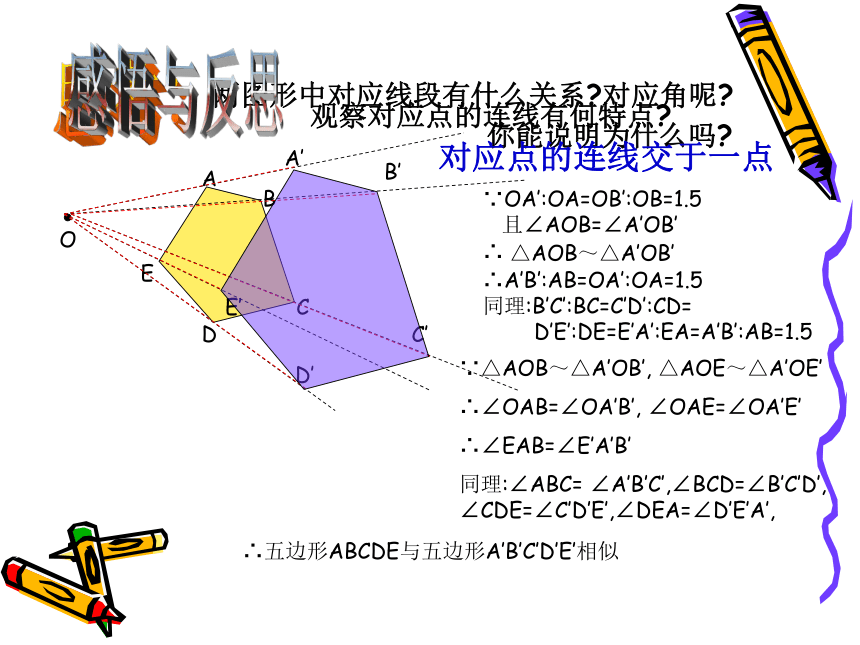
两图形中对应线段有什么关系 对应角呢
你能说明为什么吗
∴
∵OA’:OA=OB’:OB=1.5
且∠AOB=∠A’OB’
△AOB~△A’OB’
∴A’B’:AB=OA’:OA=1.5
同理:B’C’:BC=C’D’:CD=
D’E’:DE=E’A’:EA=A’B’:AB=1.5
∵△AOB~△A’OB’, △AOE~△A’OE’
∴∠OAB=∠OA’B’, ∠OAE=∠OA’E’
∴∠EAB=∠E’A’B’
同理:∠ABC= ∠A’B’C’,∠BCD=∠B’C’D’, ∠CDE=∠C’D’E’,∠DEA=∠D’E’A’,
∴五边形ABCDE与五边形A’B’C’D’E’相似
观察对应点的连线有何特点
对应点的连线交于一点
如果两个图形不仅是相似图形,而且对应顶点
的连线相交于一点,像这样的两个图形叫位似图
形,这个点叫做位似中心,这时的相似比又叫位
似比。
特征:
1、位似图形一定是相似形,反之不一定。
2、判断位似图形时要注意首先它们必须是相似形,其次每一对对应点所在直线都经过同一点。
位似是相似的特殊情况
放电影时,胶片和屏幕上的画面就形成了一种位似关系.
如:“空中的电磁波”、“水中的涟漪”、“照相时的实物与照相机中的投影”等。
利用位似,可以将一个图形放大或缩小
四种基本变换
平移
旋转
轴对称
位似
图形的形状和大小都未变
图形的形状不变,大小发生改变
位置改变,即图形运动了
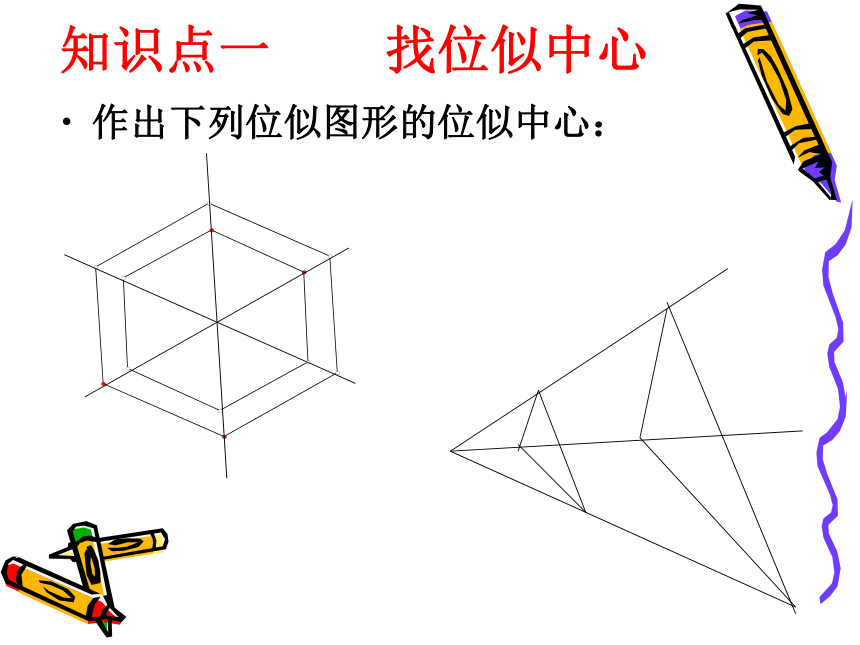
作出下列位似图形的位似中心:
知识点一 找位似中心
A
B
C
E
D
O
A’
B’
C’
D’
E’
观察所画的图,原图形和所画图形位于位似中心的
能位于位似中心的 吗
例:画四边形ABCD的相似图形,使得所画图形与原图形的相似比为2:1,且位于位似中心的两侧.
A
B
C
D
O
A’
B’
C’
D’
知识点二 画位似图形
C’
B’
A’
B’
C’
A’
B’
C’
A
B
C
位似中心是 取的,那么除了把位似中心取在形外,还可以取在那里
任意
(2)形内
(将三角形ABC放大两倍)
O
(3)多边形的一边上
A
B
C
A
B
C
.
O
(4)多边形的一个顶点
.
(O)
画位似图形怎么画
如果要将三角形ABC缩小到原来的一半,该怎么画
画位似图形的步骤:
(1)确定位似中心;
(2)画经过位似中心,且分别经过已知多边形顶点的直线;
(3)分别在各直线上取点,使其到位似中心的距离与已知多边形的对应顶点到位似中心的距离之比等于位似比;
(4)顺次连接各点,得到的图形就是所求的图形。
下列图形是否是位似图形?如果是请指出位似中心,如果不是请说明理由。
知识点三 判断位似图形
判断下面的正方形是不是位似图形?
不是
A
C
D
B
F
E
G
显然,位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形
思考:位似图形有何性质?
知识点四 位似图形的性质
性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比.
若△ABC与△A’B’C’的相似比为:1:2,则OA:OA’=( )。
O
A
A’
B
C
B’
C’
1:2
知识点四 位似图形的性质
变式:三角尺在灯泡O的照射下在墙上形成的影子(如图),现测得OA=20cm,OA`=50cm,这个三角尺的周长与它在墙上形成的影子的周长的比是____.
2:5
如图,△OAB与△OCD是位似图形,试问:(1)AB与CD平行吗?说明理由.
(2)如果OB=3,OC=4,OD=3.5,试求△OAB与△OCD的相似比及OA的长。
O
A
D
B
C
21/8
3:4
1.由位似变换得到的图形与原图形是( )
A.全等 B.相似
C.不一定相似 D.肯定不全等。
B
2.下列运动形式中:
(1)传动带上的电视机(2)电梯上的人的升降。(3)照相时底片上的投影与站在照相机前的人 。(4)国旗上的红五角星。
上述运动形式中不是位似变换的有( )
A,0个 B,1个 C,2个 D3个。
C
A
C
B
O
3、如图,△ABC与△A’B’C’是位似图形,点O是位似中心,若OA=2AA’,S△ABC=8,则S△A’B’C’=______。
A’
B’
C’
18
4、如图△ABC与△DOE是位似图形,A(0,3),B(-2,0),C(1,0),E(6,0),则D点的坐标是____, △ABC与△DOE的位似中心M的坐标是_____。
(4,6)
(-4,0)
4、一般在室外放映的电影胶片上图片的规格是3.5cm×3.5cm,放映的银屏的规格为2m×2m。若放映机的光源距胶片20cm,问:银屏应拉在距离光源多远的地方,放映的图像刚好布满整个银屏?
5、如图,在ABC内有一小正方形DEFG,若连结BG并延长交AC于N,过N作NM∥DG交AB于M,再作MQ ⊥BC于Q, NP ⊥ BC于P,于是得四边形MNPQ,试问,这两个四边形是位似图形吗?试说明理由。
1.进行位似变换后得到的图形与原图形相似,对应点的连线都经过位似中心,对应顶点到位似中心的比等于相似比
2.进行位似变换时,位似中心可以在图形的外部,也可以在图形的内部或图形的一边上,图形的顶点处
3.画已知图形的位似图形时,要明确位似中心,相似比,以及两图形在位似中心的同侧或
两侧
至此,我们已经学习了四种变换:平移、轴对称、旋转和位似,你能说出它们之间的异同吗?在图所示的图案中,你能找到这些变换吗?
课外拓展
在平面内,先将一个多边形以点O为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为k,并且原多边形上的任一点P,它的对应点P′在线段OP或其延长线上;接着将所得多边形以点O为旋转中心,逆时针旋转一个角度θ,这种经过和旋转的图形变换叫做旋转相似变换,记为O(k,θ),其中点O叫做旋转相似中心,k叫做相似比,θ叫做旋转角.
(1)填空:①如图1,将△ABC以点A为旋转相似中心,放大为原来的2倍,再逆时针旋转60°,得到△ADE,这个旋转相似变换记为A(__,__);②如图2,△ABC是边长为1cm的等边三角形,将它作旋转相似变换A(√3,90°),得到△ADE,则线段BD的长为____cm;
(2)如图3,分别以锐角三角形ABC的三边AB,BC,CA为边向外作正方形ADEB,BFGC,CHIA,点O1,O2,O3分别是这三
个正方形的对角线交点,试分别利用△AO1O3与
△ABI,△CIB与△CAO2之间的关系,运用旋转相似
变换的知识说明线段O1O3与AO2之间的关系.
课外拓展
不经历风雨,怎么见彩虹
没有人能随随便便便成功!
待续…
同学们努力吧!
A
B
A’
C’
B’
C
O
前面我们已经学习了图形的哪些变换?
平移:平移的方向,平移的距离.
旋转:旋转中心,旋转方向,旋转角度.
相似:相似比.
对称(轴对称与轴对称图形,中心对称与中心对称图形):对称轴,对称中心.
相似与轴对称,平移,旋转一样,也是图形之间的一个基本变换.可以将一个图形放大或缩小,保持形状不变,得到它的相似图形.
如何便捷的画出一个图形的相似图形呢
这节课我们学习画相似图形的一种特殊方法
下面请欣赏如下图形的变换
下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对应点的连线有什么特征?
如图,任意五边形ABCDE,你能将它放大到原来的1.5倍吗
A
B
C
E
D
1.任取一点O
O
2.以O为端点,作射线OA,OB,OC,OD,OE
3.分别在射线OA,OB,OC,OD,OE上,取点A’,B’,C’,D’,E’,使 OA’:OA=OB’:OB=OC’:OC=OD’:OD=OE’:OE=1.5
A’
B’
C’
D’
E’
4.连结A’B’,B’C’,C’D’,D’E’,E’A’,得五边形A’B’C’D’E’
E
所以,五边形A’B’C’D’E’就是所求作的五边形.
A
B
C
E
D
O
A’
B’
C’
D’
E’
两图形中对应线段有什么关系 对应角呢
你能说明为什么吗
∴
∵OA’:OA=OB’:OB=1.5
且∠AOB=∠A’OB’
△AOB~△A’OB’
∴A’B’:AB=OA’:OA=1.5
同理:B’C’:BC=C’D’:CD=
D’E’:DE=E’A’:EA=A’B’:AB=1.5
∵△AOB~△A’OB’, △AOE~△A’OE’
∴∠OAB=∠OA’B’, ∠OAE=∠OA’E’
∴∠EAB=∠E’A’B’
同理:∠ABC= ∠A’B’C’,∠BCD=∠B’C’D’, ∠CDE=∠C’D’E’,∠DEA=∠D’E’A’,
∴五边形ABCDE与五边形A’B’C’D’E’相似
观察对应点的连线有何特点
对应点的连线交于一点
如果两个图形不仅是相似图形,而且对应顶点
的连线相交于一点,像这样的两个图形叫位似图
形,这个点叫做位似中心,这时的相似比又叫位
似比。
特征:
1、位似图形一定是相似形,反之不一定。
2、判断位似图形时要注意首先它们必须是相似形,其次每一对对应点所在直线都经过同一点。
位似是相似的特殊情况
放电影时,胶片和屏幕上的画面就形成了一种位似关系.
如:“空中的电磁波”、“水中的涟漪”、“照相时的实物与照相机中的投影”等。
利用位似,可以将一个图形放大或缩小
四种基本变换
平移
旋转
轴对称
位似
图形的形状和大小都未变
图形的形状不变,大小发生改变
位置改变,即图形运动了
作出下列位似图形的位似中心:
知识点一 找位似中心
A
B
C
E
D
O
A’
B’
C’
D’
E’
观察所画的图,原图形和所画图形位于位似中心的
能位于位似中心的 吗
例:画四边形ABCD的相似图形,使得所画图形与原图形的相似比为2:1,且位于位似中心的两侧.
A
B
C
D
O
A’
B’
C’
D’
知识点二 画位似图形
C’
B’
A’
B’
C’
A’
B’
C’
A
B
C
位似中心是 取的,那么除了把位似中心取在形外,还可以取在那里
任意
(2)形内
(将三角形ABC放大两倍)
O
(3)多边形的一边上
A
B
C
A
B
C
.
O
(4)多边形的一个顶点
.
(O)
画位似图形怎么画
如果要将三角形ABC缩小到原来的一半,该怎么画
画位似图形的步骤:
(1)确定位似中心;
(2)画经过位似中心,且分别经过已知多边形顶点的直线;
(3)分别在各直线上取点,使其到位似中心的距离与已知多边形的对应顶点到位似中心的距离之比等于位似比;
(4)顺次连接各点,得到的图形就是所求的图形。
下列图形是否是位似图形?如果是请指出位似中心,如果不是请说明理由。
知识点三 判断位似图形
判断下面的正方形是不是位似图形?
不是
A
C
D
B
F
E
G
显然,位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形
思考:位似图形有何性质?
知识点四 位似图形的性质
性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比.
若△ABC与△A’B’C’的相似比为:1:2,则OA:OA’=( )。
O
A
A’
B
C
B’
C’
1:2
知识点四 位似图形的性质
变式:三角尺在灯泡O的照射下在墙上形成的影子(如图),现测得OA=20cm,OA`=50cm,这个三角尺的周长与它在墙上形成的影子的周长的比是____.
2:5
如图,△OAB与△OCD是位似图形,试问:(1)AB与CD平行吗?说明理由.
(2)如果OB=3,OC=4,OD=3.5,试求△OAB与△OCD的相似比及OA的长。
O
A
D
B
C
21/8
3:4
1.由位似变换得到的图形与原图形是( )
A.全等 B.相似
C.不一定相似 D.肯定不全等。
B
2.下列运动形式中:
(1)传动带上的电视机(2)电梯上的人的升降。(3)照相时底片上的投影与站在照相机前的人 。(4)国旗上的红五角星。
上述运动形式中不是位似变换的有( )
A,0个 B,1个 C,2个 D3个。
C
A
C
B
O
3、如图,△ABC与△A’B’C’是位似图形,点O是位似中心,若OA=2AA’,S△ABC=8,则S△A’B’C’=______。
A’
B’
C’
18
4、如图△ABC与△DOE是位似图形,A(0,3),B(-2,0),C(1,0),E(6,0),则D点的坐标是____, △ABC与△DOE的位似中心M的坐标是_____。
(4,6)
(-4,0)
4、一般在室外放映的电影胶片上图片的规格是3.5cm×3.5cm,放映的银屏的规格为2m×2m。若放映机的光源距胶片20cm,问:银屏应拉在距离光源多远的地方,放映的图像刚好布满整个银屏?
5、如图,在ABC内有一小正方形DEFG,若连结BG并延长交AC于N,过N作NM∥DG交AB于M,再作MQ ⊥BC于Q, NP ⊥ BC于P,于是得四边形MNPQ,试问,这两个四边形是位似图形吗?试说明理由。
1.进行位似变换后得到的图形与原图形相似,对应点的连线都经过位似中心,对应顶点到位似中心的比等于相似比
2.进行位似变换时,位似中心可以在图形的外部,也可以在图形的内部或图形的一边上,图形的顶点处
3.画已知图形的位似图形时,要明确位似中心,相似比,以及两图形在位似中心的同侧或
两侧
至此,我们已经学习了四种变换:平移、轴对称、旋转和位似,你能说出它们之间的异同吗?在图所示的图案中,你能找到这些变换吗?
课外拓展
在平面内,先将一个多边形以点O为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为k,并且原多边形上的任一点P,它的对应点P′在线段OP或其延长线上;接着将所得多边形以点O为旋转中心,逆时针旋转一个角度θ,这种经过和旋转的图形变换叫做旋转相似变换,记为O(k,θ),其中点O叫做旋转相似中心,k叫做相似比,θ叫做旋转角.
(1)填空:①如图1,将△ABC以点A为旋转相似中心,放大为原来的2倍,再逆时针旋转60°,得到△ADE,这个旋转相似变换记为A(__,__);②如图2,△ABC是边长为1cm的等边三角形,将它作旋转相似变换A(√3,90°),得到△ADE,则线段BD的长为____cm;
(2)如图3,分别以锐角三角形ABC的三边AB,BC,CA为边向外作正方形ADEB,BFGC,CHIA,点O1,O2,O3分别是这三
个正方形的对角线交点,试分别利用△AO1O3与
△ABI,△CIB与△CAO2之间的关系,运用旋转相似
变换的知识说明线段O1O3与AO2之间的关系.
课外拓展
不经历风雨,怎么见彩虹
没有人能随随便便便成功!
待续…
同学们努力吧!
