等比数列
图片预览









文档简介
(共51张PPT)
等比数列
复习与提问:
1、等差数列的定义:
定义的符号表示:
2、等差数列的通项公式:
3、等差中项:a,A,b成等差数列,则
A=(a+b)/2
an = a1 +(n-1)d
等差数列 an+1-an=d
一个数列从第2项起,每一项与前一项的差等于同一个常数,这个数列叫做等差数列.
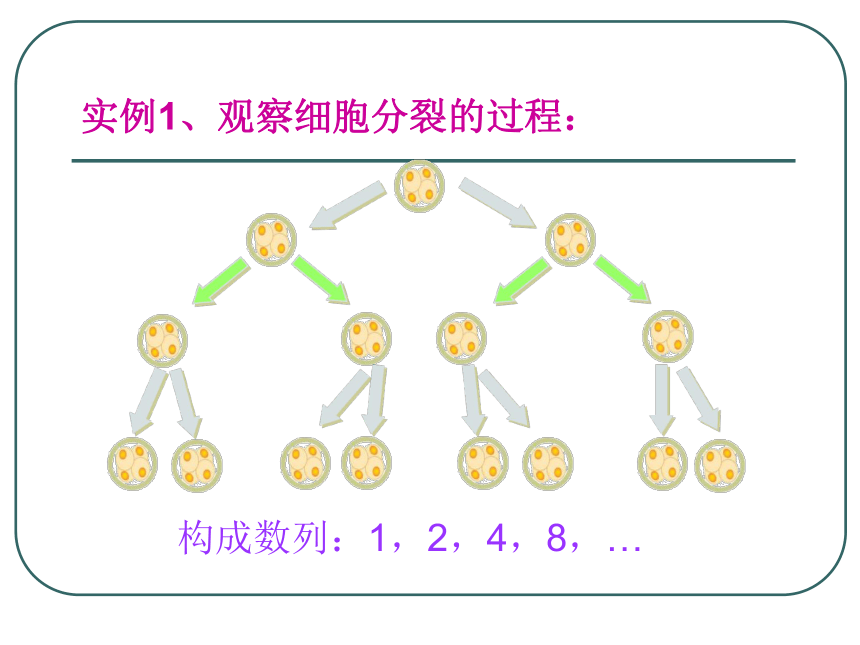
实例1、观察细胞分裂的过程:
构成数列:1,2,4,8,…
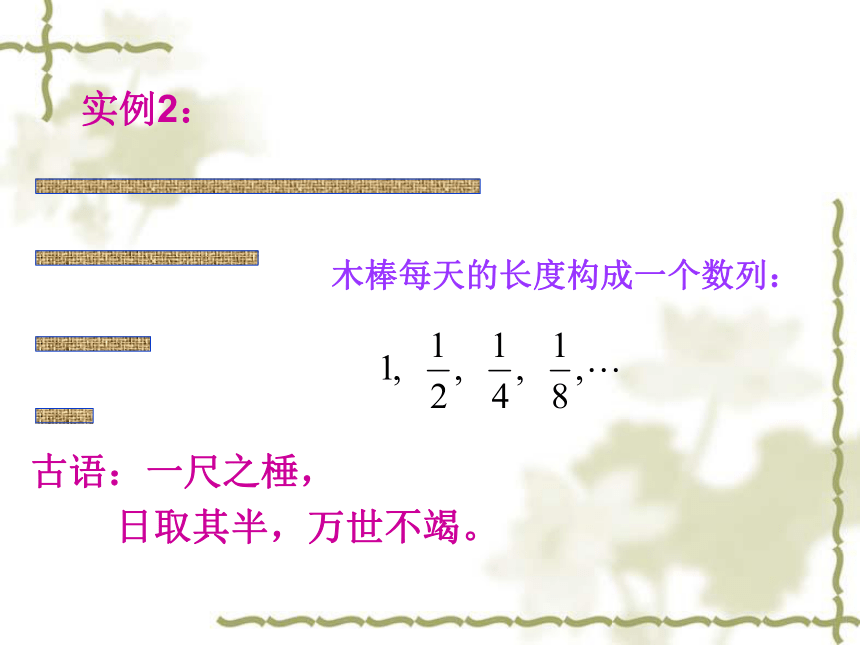
古语:一尺之棰,
日取其半,万世不竭。
木棒每天的长度构成一个数列:
实例2:
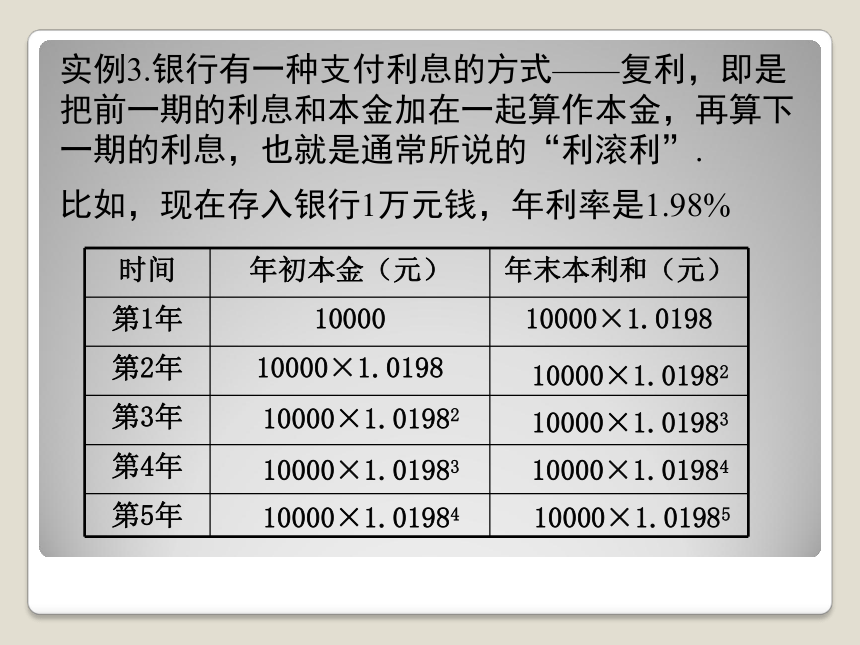
实例3.银行有一种支付利息的方式——复利,即是把前一期的利息和本金加在一起算作本金,再算下一期的利息,也就是通常所说的“利滚利”.
比如,现在存入银行1万元钱,年利率是1.98%
时间 年初本金(元) 年末本利和(元)
第1年 10000 10000×1.0198
第2年 10000×1.0198
第3年
第4年
第5年
10000×1.01982
10000×1.01982
10000×1.01983
10000×1.01983
10000×1.01984
10000×1.01984
10000×1.01985
①1,2,4,8,…
②
③1,20,202,203…
④ 10000×1.01981 , 10000×1.01982 , 10000×1.01983 , 10000×1.01984…
共同特点:从第2项起,每一项与前一项的比都等于同一个常数。
思考:以下数列有什么共同特点?
定义
等比数列:
从第 2 项起,每一项与前一项的比等于同一个常数
如果一个数列
,那么这个数列就叫做等比数列。
这个常数叫做等比数列的公比,公差通常用字母 q 表示.
即: (q常数) (n≥2)
① -2,1,4,7,10,13,16,19,…
② 4,16,32,64,128,256,…
③ 243,81,27,9,3,1,,,…
④ 3,3,3,3,3,3,3,…
练习1、你能举出一些等比数列的例子吗?
q=1
练习2、指出下列数列是不是等比数列,若是,请说出其公比是多少:
×
×
练习:课本52页 2
练习:课本53页 5(1)
思考1:等比数列的公比q能取0吗?
×
(4)等比数列的数学语言定义中: 无法用
替代。
对等比数列的认识:
(2)等比数列的每一项都不为0,即 ;
(1)等比数列的首项不为0;
(3)公比不为0.
思考2:公比q<0时,等比数列呈现怎样的特点?
正负交替
对公比q的探究: (a1 ﹥0时)
当0﹤q﹤1时,等比数列{an}为递减数列;
当q﹥1时,等比数列{an}为递增数列;
当q=1时,等比数列{an}为常数列;
当q﹤0时,等比数列{an}为摆动数列。
思考3:有无数列是既等比又等差的?
注意:当 时,数列 既是等差又是等比数列,当 时,它只是等差数列,而不是等比数列.
等比中项:
如果a,G,b成等比数列,那么G叫做a与b的等比中项。
a,G,b成等比数列
例:-1和10是否存在等比中项,是的话如何计算?
思考:类比等差中项,什么是等比中项?
对a,b的要求:a,b要同号。
练习:课本54页 A组7
练习:课本54页 A组6
如果等比数列 { }的首项是 ,公比是 ,那么这个等比数列的第 项 如何表示
当n=1时,
(等比数列通项公式)
如果等比数列 { }的首项是 ,公比是,那么这个等比数列的第 项 如何表示
,… ,
∵
∴
…
如何对其加以严格的证明呢?
想一想?
证明:
将等式左右两边分别相乘可得:
化简得:
即:
此式对n=1也成立
∵
,… ,
……
……
∴
叠乘法推导
已知数列{an}为等比数列,其首项为a1 ,公比为q,
则其通项公式为:
通项公式
练习:课本54页 A组8
从通项公式,想象一下等比数列的图象是怎么样的吗?
o
1
2
3
4
5
6
1
2
3
4
5
6
7
8
等比数列通项公式的图象表示:
课本50页探究(2)
通项公式
数学式
子表示
定 义
等比数列
等差数列
名 称
如果一个数列从第2项起,每一项与前一项的差等于同一个常数,那么这个数列叫做等差数列.这个常数叫做等差数列的公差,用d表示
an+1-an=d
an = a1 +(n-1)d
如果一个数列从第2项起,每一项与它前一项的比都等于同一个常数,那么这个数列叫做等比数列.这个常数叫做等比数列的公比,用q表示
1.求下列等比数列的第4,5项:
②1.2,2.4,4.8,…
①5,-15,45,…
三.巩固 应用
变形1、等比数列{an}中,a1=2,q=-3,求a8与an.
变形2、等比数列{an}中,a1=2, a9=32,求q.
2.在等比数列{an}中,已知
求an.
例1:某种放射性物质不断变化为其他物质,每
经过一年剩留的这种物质是原来的84%,这种物质的半
衰期为多长(精确到1年)?
分析:
时间: 剩留量:
最初 1
经过1年a1=0.84
经过2年a2=0.842
经过3年a3=0.843
经过n年an=0.84n
二.等比数列通项公式的应用
把③代入① ,得
把②的两边分别除以①的两边,得
解:设这个等比数列的第1项是 ,公比是 ,那么
①
②
例2、 一个等比数列的第3项与第4项分别是12与18,求它的第1项与第2项.
例3:根据图2-4-2中的框图,
写出所打印数列的前5项,
并建立数列的递推公式,
这个数列是等比数列吗?
开始
A=1
n=1
输出A
n=n+1
n>5
结束
是
A=A×(1/2)
否
是项数相同的等比数列,
求证:
是等比数列
练习:课本53页 3
练习:课本53页 A组3
补充例题
在等比数列{an}中,若已知某一项为am,公比为q, 求该数列的任意项an。
等比数列通项公式的推广公式:
an=amqn-m
(am≠0,an ≠ 0,m,n∈N*)
题型1:
例、等比数列{an}中,a1+a3=10,a4+a6=5/4, 求q的值.
例、等比数列{an}中,a3+ a6=36,a4+a7=18, an =1/2,求n.
练习:课本52页 1
练习:课本54页 B组1
方法1:利用通项公式
例2:一个等比数列的第2项与第4项分别是8与18,求它的第3项。
在等比数列{an}中,若已知某两项am、 an,求其中任意一项。
题型2:
方法2:利用定义
在等比数列中,当m+n=p+q(m,n,p,q )时,有
9
±3
81
练习:课本53页 4(1)
总结
1.定义
2.公比(差)
3.等比(差)
中项
4.通项公式
5.性质
(若m+n=p+q)
q不可以是0,
d可以是0
等比中项
等差中项
等差数列(A P)
等比数列(G P)
练习:课本54页 A4
报纸能比泰山高吗?
(1)假设我们有一张足够大的报纸.(设报纸厚度是a米). 先把报纸对折一次,这时纸张的厚度是报纸单页的2倍.即2a米
(2)我们再将报纸对折一次,纸张的厚度变为:
4a米即2 a米
第三次再对折后报纸的厚度是:
8a米即2 a米
(3) 三次折叠,报纸厚度分别是:
2a米,2 a米,2 a米
我们猜想,继续这样折叠,报纸的厚度会是
一组等比数列:
2 a, 2 a, 2 a , 2 a, 2 a, 2 a …
(4)假设报纸的单页厚度约为0.1毫米,
需要折叠几次才能比泰山高呢?
(4)可以测得报纸的单页厚度约为0.1毫米 (即a=0.0001m),当我们把报纸折叠了21次,此时的厚度是:
2 a = 2097152毫米 = 2097.152米
报纸的厚度高过泰山500多米!
等比数列
复习与提问:
1、等差数列的定义:
定义的符号表示:
2、等差数列的通项公式:
3、等差中项:a,A,b成等差数列,则
A=(a+b)/2
an = a1 +(n-1)d
等差数列 an+1-an=d
一个数列从第2项起,每一项与前一项的差等于同一个常数,这个数列叫做等差数列.
实例1、观察细胞分裂的过程:
构成数列:1,2,4,8,…
古语:一尺之棰,
日取其半,万世不竭。
木棒每天的长度构成一个数列:
实例2:
实例3.银行有一种支付利息的方式——复利,即是把前一期的利息和本金加在一起算作本金,再算下一期的利息,也就是通常所说的“利滚利”.
比如,现在存入银行1万元钱,年利率是1.98%
时间 年初本金(元) 年末本利和(元)
第1年 10000 10000×1.0198
第2年 10000×1.0198
第3年
第4年
第5年
10000×1.01982
10000×1.01982
10000×1.01983
10000×1.01983
10000×1.01984
10000×1.01984
10000×1.01985
①1,2,4,8,…
②
③1,20,202,203…
④ 10000×1.01981 , 10000×1.01982 , 10000×1.01983 , 10000×1.01984…
共同特点:从第2项起,每一项与前一项的比都等于同一个常数。
思考:以下数列有什么共同特点?
定义
等比数列:
从第 2 项起,每一项与前一项的比等于同一个常数
如果一个数列
,那么这个数列就叫做等比数列。
这个常数叫做等比数列的公比,公差通常用字母 q 表示.
即: (q常数) (n≥2)
① -2,1,4,7,10,13,16,19,…
② 4,16,32,64,128,256,…
③ 243,81,27,9,3,1,,,…
④ 3,3,3,3,3,3,3,…
练习1、你能举出一些等比数列的例子吗?
q=1
练习2、指出下列数列是不是等比数列,若是,请说出其公比是多少:
×
×
练习:课本52页 2
练习:课本53页 5(1)
思考1:等比数列的公比q能取0吗?
×
(4)等比数列的数学语言定义中: 无法用
替代。
对等比数列的认识:
(2)等比数列的每一项都不为0,即 ;
(1)等比数列的首项不为0;
(3)公比不为0.
思考2:公比q<0时,等比数列呈现怎样的特点?
正负交替
对公比q的探究: (a1 ﹥0时)
当0﹤q﹤1时,等比数列{an}为递减数列;
当q﹥1时,等比数列{an}为递增数列;
当q=1时,等比数列{an}为常数列;
当q﹤0时,等比数列{an}为摆动数列。
思考3:有无数列是既等比又等差的?
注意:当 时,数列 既是等差又是等比数列,当 时,它只是等差数列,而不是等比数列.
等比中项:
如果a,G,b成等比数列,那么G叫做a与b的等比中项。
a,G,b成等比数列
例:-1和10是否存在等比中项,是的话如何计算?
思考:类比等差中项,什么是等比中项?
对a,b的要求:a,b要同号。
练习:课本54页 A组7
练习:课本54页 A组6
如果等比数列 { }的首项是 ,公比是 ,那么这个等比数列的第 项 如何表示
当n=1时,
(等比数列通项公式)
如果等比数列 { }的首项是 ,公比是,那么这个等比数列的第 项 如何表示
,… ,
∵
∴
…
如何对其加以严格的证明呢?
想一想?
证明:
将等式左右两边分别相乘可得:
化简得:
即:
此式对n=1也成立
∵
,… ,
……
……
∴
叠乘法推导
已知数列{an}为等比数列,其首项为a1 ,公比为q,
则其通项公式为:
通项公式
练习:课本54页 A组8
从通项公式,想象一下等比数列的图象是怎么样的吗?
o
1
2
3
4
5
6
1
2
3
4
5
6
7
8
等比数列通项公式的图象表示:
课本50页探究(2)
通项公式
数学式
子表示
定 义
等比数列
等差数列
名 称
如果一个数列从第2项起,每一项与前一项的差等于同一个常数,那么这个数列叫做等差数列.这个常数叫做等差数列的公差,用d表示
an+1-an=d
an = a1 +(n-1)d
如果一个数列从第2项起,每一项与它前一项的比都等于同一个常数,那么这个数列叫做等比数列.这个常数叫做等比数列的公比,用q表示
1.求下列等比数列的第4,5项:
②1.2,2.4,4.8,…
①5,-15,45,…
三.巩固 应用
变形1、等比数列{an}中,a1=2,q=-3,求a8与an.
变形2、等比数列{an}中,a1=2, a9=32,求q.
2.在等比数列{an}中,已知
求an.
例1:某种放射性物质不断变化为其他物质,每
经过一年剩留的这种物质是原来的84%,这种物质的半
衰期为多长(精确到1年)?
分析:
时间: 剩留量:
最初 1
经过1年a1=0.84
经过2年a2=0.842
经过3年a3=0.843
经过n年an=0.84n
二.等比数列通项公式的应用
把③代入① ,得
把②的两边分别除以①的两边,得
解:设这个等比数列的第1项是 ,公比是 ,那么
①
②
例2、 一个等比数列的第3项与第4项分别是12与18,求它的第1项与第2项.
例3:根据图2-4-2中的框图,
写出所打印数列的前5项,
并建立数列的递推公式,
这个数列是等比数列吗?
开始
A=1
n=1
输出A
n=n+1
n>5
结束
是
A=A×(1/2)
否
是项数相同的等比数列,
求证:
是等比数列
练习:课本53页 3
练习:课本53页 A组3
补充例题
在等比数列{an}中,若已知某一项为am,公比为q, 求该数列的任意项an。
等比数列通项公式的推广公式:
an=amqn-m
(am≠0,an ≠ 0,m,n∈N*)
题型1:
例、等比数列{an}中,a1+a3=10,a4+a6=5/4, 求q的值.
例、等比数列{an}中,a3+ a6=36,a4+a7=18, an =1/2,求n.
练习:课本52页 1
练习:课本54页 B组1
方法1:利用通项公式
例2:一个等比数列的第2项与第4项分别是8与18,求它的第3项。
在等比数列{an}中,若已知某两项am、 an,求其中任意一项。
题型2:
方法2:利用定义
在等比数列中,当m+n=p+q(m,n,p,q )时,有
9
±3
81
练习:课本53页 4(1)
总结
1.定义
2.公比(差)
3.等比(差)
中项
4.通项公式
5.性质
(若m+n=p+q)
q不可以是0,
d可以是0
等比中项
等差中项
等差数列(A P)
等比数列(G P)
练习:课本54页 A4
报纸能比泰山高吗?
(1)假设我们有一张足够大的报纸.(设报纸厚度是a米). 先把报纸对折一次,这时纸张的厚度是报纸单页的2倍.即2a米
(2)我们再将报纸对折一次,纸张的厚度变为:
4a米即2 a米
第三次再对折后报纸的厚度是:
8a米即2 a米
(3) 三次折叠,报纸厚度分别是:
2a米,2 a米,2 a米
我们猜想,继续这样折叠,报纸的厚度会是
一组等比数列:
2 a, 2 a, 2 a , 2 a, 2 a, 2 a …
(4)假设报纸的单页厚度约为0.1毫米,
需要折叠几次才能比泰山高呢?
(4)可以测得报纸的单页厚度约为0.1毫米 (即a=0.0001m),当我们把报纸折叠了21次,此时的厚度是:
2 a = 2097152毫米 = 2097.152米
报纸的厚度高过泰山500多米!
