不等关系与不等式

(共45张PPT)
实际生活中
长短
大小
轻重
高矮
一.问题情境
横看成岭侧成峰
远近高低各不同
雷声大，雨点小
捡了芝麻，丢了西瓜
道高一尺，魔高一丈
三个臭皮匠，抵过一个诸葛亮
你能发现下列成语、谚语中反映的不等关系吗
我们生活中的到处都有不等关系
说一说
在数学中我们如何表示不等关系
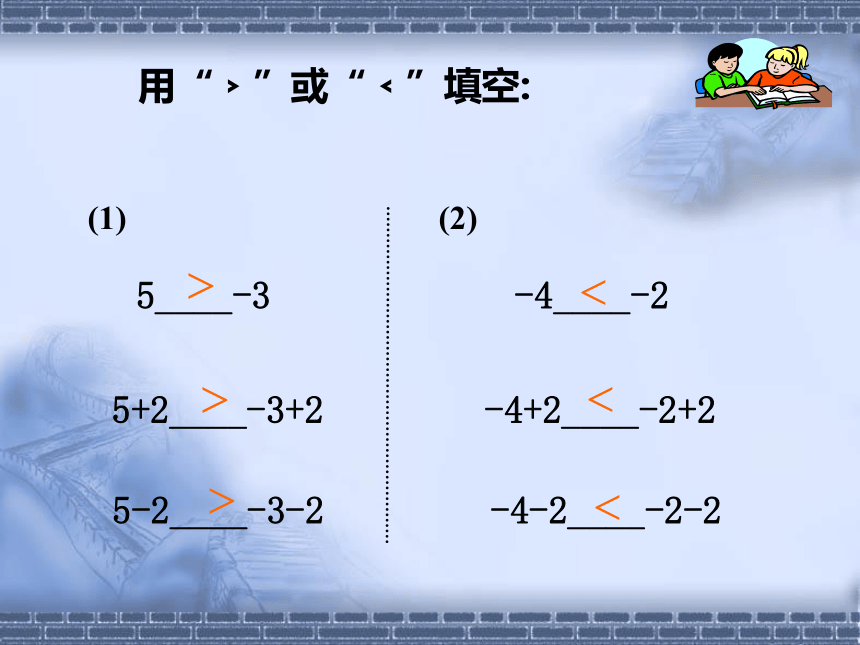
用“﹥”或“﹤”填空:
(2)
5+2____-3+2
5-2____-3-2
-4+2____-2+2
-4-2____-2-2
5____-3
-4____-2
1、天气预报说：明天的最高气温为13℃，最低气温为7℃，则温度t必须满足什么？
2、a是一个非负实数。
7℃≤t≤13℃
a≥0（a∈R）
3. 雷电的温度大约是28000℃，比太阳
表面温度的4.5倍还要高。设太阳表面温度为t ℃，
那么t应满足怎样的关系式？
4.5t<28000
4. 这是某酸奶的质量检查规定
脂肪含量（f） 蛋白质含量（p）
不少于2.5％ 不少于2.3％
用数学关系来反映就是：
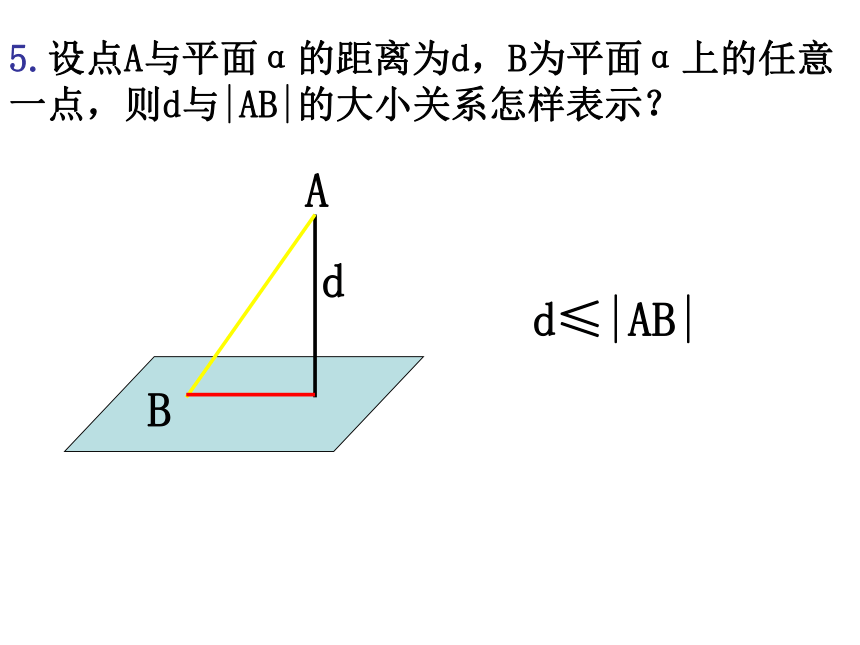
5.设点A与平面α的距离为d，B为平面α上的任意一点，则d与|AB|的大小关系怎样表示？
d≤|AB|
A
B
d
必修5 第74页
问题：如果19人去该如何购票？
19人的普通票花费
190元
若选择20人的团体票花费
160元
是否选择团体票就一定实惠？
那么满足什么样的不等关系时，消费者能得到更大实惠？
例1.博物馆的门票每张10元，20人以上（含20人）的团体票8折优惠，那在不足20人时，选择怎样的购票策略？（不求解）
数学应用
例1.博物馆的门票每张10元，20人以上（含20人）的团体票8折优惠，那在不足20人时，选择怎样的购票策略？（不求解）
解：设x人(x<20)买20人的团体票比普通票便宜，则有
　　　　
　8×20≤10x
（这是一次不等式问题）
数学应用
数学应用
例.某种杂志原以每本2.5元的价格销售，可以售出8万本。据市场调查，若单价每提高0.1元销售量就可能相应减少2000本。若每本定价x元，怎样用不等式表示销售的总收入仍不低于20万元呢？
分析：若杂志的定价为x元，则销售量减少：
X-2.5
0.1
×
0.2
万本
因此，销售总收入为：
X-2.5
0.1
×
0.2
8
-
X
万元
数学应用
例.某种杂志原以每本2.5元的价格销售，可以售出8万本。据市场调查，若单价每提高0.1元销售量就可能相应减少2000本。若每本提价0.1元，怎样用不等式表示销售的总收入仍不低于20万元呢？
∴用不等式表示为：
X-2.5
0.1
×
0.2
8
-
X
≥20
化简得：
（这是一个一元二次不等式问题）
例、某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格.按照生产的要求，600mm的钢管的数量不能超过500mm钢管的3倍。怎样写出满足上述所有不等关系的不等式呢？
(3)截得两种钢管的数量都不能为负.
(1)截得600mm钢管的数量不能超过500mm的钢管数量的3倍；
(2)截得两种钢管的总长度不能超过4000mm；
例、某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格.按照生产的要求，600mm的钢管的数量不能超过500mm钢管的3倍。怎样写出满足上述所有不等关系的不等式呢？
（这是一个一元一次不等式组问题）
建构数学
实际问题：不等关系
数学问题：不等式
抽象
概括
刻画
什么是不等式（组）
在数轴上，如果表示实数a和b的两个点分别为A和B，则右边点对应的实数比左边点对应的实数大,而且点A和点B在数轴上的位置关系有以下三种：
（1）点A和点B重合；（2）点A在点B的右侧；
（3）点A在点B的左侧.
在这三种位置关系中，有且仅有一种成立，由此可得到结论：
对于任意两个实数a和b，在a=b，a>b，a如果a－b是正数，则a>b；如果a>b，则a－b为正数；
如果a－b是负数，则a如果a－b等于零，则a=b；如果a=b，则a－b等于零.
通常，“如果p，则q”为正确命题，则简记为 ，读作“p推出q”.
如果 都是正确的命题，记为
读作“p等价于q或q等价于p”.
上述结论可以写成：
作差→变形→判断符号→确定大小.
作差比较法其一般步骤是:
例．比较x2－x与x－2的大小.
解：(x2－x)－(x－2)=
因为(x－1)2≥0，
所以(x2－x)－(x－2)>0，
因此x2－x>x－2.
x2－2x+2
=(x－1)2+1，
课本75页A2
课本75页B 1 （3）（4）
探究：不等式的基本性质
思考1：若甲的身材比乙高，则乙的身材比甲矮，反之亦然.从数学的观点分析，这里反映了一个不等式性质。
a＞b b＜a
（对称性）
性质1：如果a > b，那么b < a，如果b < a，那么a > b．(对称性)
即：a > b b < a；b < a a > b．
证明:
即：a>b b思考2：若甲的身材比乙高，乙的身材比丙高，那么甲的身材与丙的有什么大小关系？
性质2：如果a > b，且b > c，那么a > c．(传递性)
即：a > b，b > c a > c．
说明：这是不等式的传递性、这种传递性可以推广到n个的情形．
证明:
思考3：若甲的年薪比乙高，如果年终两人发同样多的奖金，则甲、乙最终谁拿到的钱多？
性质3：如果a > b，那么a + c > b + c．
即：a > b a + c > b + c．(可加性)
证明:
性质3表明，不等式的两边都加上同一个实数，所得的不等式与原不等式同向.
a+b>c a+b+(－b)>c+(－b) a>c－b.
由性质3可以得出
推论1：不等式中的任意一项都可以把它的符号变成相反的符号后，从不等式的一边移到另一边。 （移项法则）
思考4：若甲班的男生比乙班多，甲班的女生也比乙班多，则甲班的人数比乙班人数谁多？
性质4：如果a > b，且c > d，
那么a + c > b + d．(同向可加法则)
即：a > b，c > d a + c > b + d．
证明:
注意：
性质4：如果a > b，且c > d，
那么a + c > b + d．(同向可加法法则)
即：a > b，c > d a + c > b + d．
(1) 这一推论可以推广到任意有限个同向不等式两边分别相加，即：
两个或多个同向不等式两边分别相加，所得不等式与原不等式同向；
(2) 两个同向不等式的两边分别相减时，不能作出一般的结论．
思考5：如果a＞b，那么ac>bc吗？
如果a＞b，c>0，那么ac与bc的大小关系如何？
a＞b，c＞0 ac＞bc；
a＞b，c＜0 ac＜bc
(可乘性)
证明:
思考6：如果a＞b＞0，c＞d＞0，那么ac与bd的大小关系如何？为什么？
a＞b＞0，c＞d＞0 ac＞bd
(乘法法则)
思考7：如果a＞b＞0，n∈N*，那么an与bn的大小关系如何？
a＞b＞0 an＞bn (n∈N*)
（乘方法则）
证明：因为
个，
根据乘法法则，得an>bn.
思考8：如果a＞b＞0，n∈N*，那么 与 的大小关系如何？
a＞b＞0 ＞ (n∈N*)
（开方法则）
证明：用反证法，假定 ，即
或 ，
根据乘方性质，得
即：a这都与a>b矛盾，因此
运用性质
倒
数
性
质
例1 已知a＞b＞0，c＜0，
求证: .
课本75页A3
课本75页B2
变式练习：应用不等式的性质，证明下列不等式：
（1）已知a>b，ab>0，求证： ；
证明：
（1）因为ab>0，所以
又因为a>b，所以
即
因此
（2）已知a>b， cb－d；
证明：（2）因为a>b，c所以a>b，－c>－d，
根据同向可加性，得
a+(－c)>b+(－d)，即a－c>b－d.
（3）已知a>b>0，0证明：（3）因为0又因为a>b>0，所以
即