北师大版高中数学必修1第三章4.1 对数的运算性 课件(共27张PPT)
文档属性
| 名称 | 北师大版高中数学必修1第三章4.1 对数的运算性 课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-14 19:53:02 | ||
图片预览







文档简介
(共27张PPT)
教
学
课
件
对数的运算性质
北师大版高中数学必修1第三章第四节第二课时
环节一
预习展示
揭示课题
Specific
Objective
Establishment
&
Preview
Achievement
Show
Ⅰ
预习展示
请各学习小组展示预习成果
提升
交流
自主
揭示课题
问题情境:
科学家以里氏震级来度量地震的强度.若设I为地震时所散发出来的相对能量程度,则里氏震级r可定义为r=0.6lgI,
试比较唐山大地震(7.8级)和汶川大地震(8.0级)的相对能量程度.
环节二
目标导学
合作探究
Comment
,
Problem
Solving
&
Improvement
Ⅱ
明确目标
合作探究
学生分小组探究对数运算性质。
探究一:
1.填出下表各组的值,并从数据中分析等量关系,猜想对数的运算性质
动手实践
第一组
式
log28
log232
log2(8×32)
值
猜想性质
3
5
8
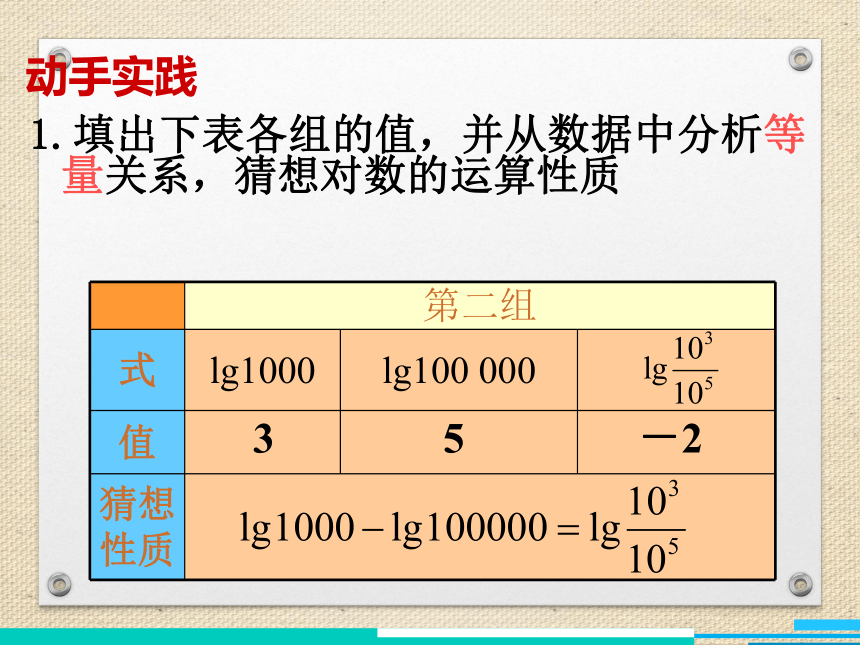
1.填出下表各组的值,并从数据中分析等量关系,猜想对数的运算性质
动手实践
第二组
式
lg1000
lg100
000
值
猜想性质
3
-2
5
1.填出下表各组的值,并从数据中分析等量关系,猜想对数的运算性质
动手实践
第三组
式
log335
5·log33
值
猜想性质
5
5
2,利用科学计算器,完成下表(精确到0.000001)并从数据中分析等量关系,猜想对数的运算性质
1.003937
1.144846
1.305865
0.012952
0.062906
0.397940
lgM-lgN
0.012952
0.062906
0.397940
10.865471
0.215910
2.210411
lgM·lgN
6.592576
0.931445
3
lgM+lgN
6.592576
0.931445
3
lg(MN)
1949
2.718281
20
N
2008
3.141596
50
M
小组交流
请各学习小组展示探究成果
对数的运算性质
前提:如果a>0且a≠1,M>0,N>0
,则:
(1)
(2)
(3)
积对数等于对数之和.
商对数等于对数之差.
n次幂的对数等于n倍的对数.
对数的运算性质证明
性质证明
小试牛刀
请你仿照性质(1)证明,证明性质
(2)和性质(3)
环节三
检测反馈
目标达成
Test
,
Self-examination
&
Goal
Attainment
Ⅲ
例1
计算
探究二:对数运算性质应用
例2
用logax,logay,logaz表示下列各式:
思考交流
1.判断下列各式是否成立,如果不成立,举一个反例.
2.对数的运算性质有什么特点?
环节四
课堂小结
课外拓展
Brief
Summary
&
Expanding
Ⅳ
谈谈
收获
1.
对数的运算性质
前提:如果a>0,a≠1,M>0,N>0
,则:
(1)
推而广之:
谈谈
收获
2.
灵活运用对数的运算性质来解决实际问题.
(2)
(3)
1、看课本P80-83的内容。
2、做课本:P83的练习2的第
2、3题。
P87
习题A组5、6.
3、选做题:步步高40分钟课时训练。
祝同学们学习进步!
例3
科学家以里氏震级来度量地震的强度.若设I为地震时所散发出来的相对能量程度,则里氏震级r可定义为r=0.6lgI,试比较8.0级和7.8级地震的相对能量程度.
解
设8.0级和7.8级地震的相对能量程度分别为I1和I2,由题意得
8.0=0.6lgI1
7.8=0.6lgI2
0.6(lgI1-lgI2
)=0.2
练习
1.求下列等式中的x的值:
(1)logx81=2;
(2)lg0.001=x;
(3)10x+lg2=2000.
2.求下列各式的值:
9
-3
3
-2
2
2
2
0
1.5
3.用lgx,lgy,lgz表示下列各式:
练习
(1)2lgx+lgy+3lgz
完成课本P82-83的思考交流.
教
学
课
件
对数的运算性质
北师大版高中数学必修1第三章第四节第二课时
环节一
预习展示
揭示课题
Specific
Objective
Establishment
&
Preview
Achievement
Show
Ⅰ
预习展示
请各学习小组展示预习成果
提升
交流
自主
揭示课题
问题情境:
科学家以里氏震级来度量地震的强度.若设I为地震时所散发出来的相对能量程度,则里氏震级r可定义为r=0.6lgI,
试比较唐山大地震(7.8级)和汶川大地震(8.0级)的相对能量程度.
环节二
目标导学
合作探究
Comment
,
Problem
Solving
&
Improvement
Ⅱ
明确目标
合作探究
学生分小组探究对数运算性质。
探究一:
1.填出下表各组的值,并从数据中分析等量关系,猜想对数的运算性质
动手实践
第一组
式
log28
log232
log2(8×32)
值
猜想性质
3
5
8
1.填出下表各组的值,并从数据中分析等量关系,猜想对数的运算性质
动手实践
第二组
式
lg1000
lg100
000
值
猜想性质
3
-2
5
1.填出下表各组的值,并从数据中分析等量关系,猜想对数的运算性质
动手实践
第三组
式
log335
5·log33
值
猜想性质
5
5
2,利用科学计算器,完成下表(精确到0.000001)并从数据中分析等量关系,猜想对数的运算性质
1.003937
1.144846
1.305865
0.012952
0.062906
0.397940
lgM-lgN
0.012952
0.062906
0.397940
10.865471
0.215910
2.210411
lgM·lgN
6.592576
0.931445
3
lgM+lgN
6.592576
0.931445
3
lg(MN)
1949
2.718281
20
N
2008
3.141596
50
M
小组交流
请各学习小组展示探究成果
对数的运算性质
前提:如果a>0且a≠1,M>0,N>0
,则:
(1)
(2)
(3)
积对数等于对数之和.
商对数等于对数之差.
n次幂的对数等于n倍的对数.
对数的运算性质证明
性质证明
小试牛刀
请你仿照性质(1)证明,证明性质
(2)和性质(3)
环节三
检测反馈
目标达成
Test
,
Self-examination
&
Goal
Attainment
Ⅲ
例1
计算
探究二:对数运算性质应用
例2
用logax,logay,logaz表示下列各式:
思考交流
1.判断下列各式是否成立,如果不成立,举一个反例.
2.对数的运算性质有什么特点?
环节四
课堂小结
课外拓展
Brief
Summary
&
Expanding
Ⅳ
谈谈
收获
1.
对数的运算性质
前提:如果a>0,a≠1,M>0,N>0
,则:
(1)
推而广之:
谈谈
收获
2.
灵活运用对数的运算性质来解决实际问题.
(2)
(3)
1、看课本P80-83的内容。
2、做课本:P83的练习2的第
2、3题。
P87
习题A组5、6.
3、选做题:步步高40分钟课时训练。
祝同学们学习进步!
例3
科学家以里氏震级来度量地震的强度.若设I为地震时所散发出来的相对能量程度,则里氏震级r可定义为r=0.6lgI,试比较8.0级和7.8级地震的相对能量程度.
解
设8.0级和7.8级地震的相对能量程度分别为I1和I2,由题意得
8.0=0.6lgI1
7.8=0.6lgI2
0.6(lgI1-lgI2
)=0.2
练习
1.求下列等式中的x的值:
(1)logx81=2;
(2)lg0.001=x;
(3)10x+lg2=2000.
2.求下列各式的值:
9
-3
3
-2
2
2
2
0
1.5
3.用lgx,lgy,lgz表示下列各式:
练习
(1)2lgx+lgy+3lgz
完成课本P82-83的思考交流.
