5.3 应用二元一次方程组——鸡兔同笼(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 5.3 应用二元一次方程组——鸡兔同笼(知识清单+经典例题+夯实基础+提优特训+中考链接) |  | |
| 格式 | zip | ||
| 文件大小 | 405.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-15 18:04:15 | ||
图片预览



文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
北师大版2020-2021学年度上学期八年级数学上册第五章二元一次方程组
5.3
应用二元一次方程组——鸡兔同笼
【知识清单】
1.
列方程组解决实际问题的一般步骤:
(1)审:认真审题,弄清问题中已知量和未知量;问题给出和涉及的相等关系是什么.
(2)找:找出问题给出和涉及的(两个)等量关系;
(3)设:(未知数).用字母表示题中的两个未知数;设未知数分为①直接未知数;②间接未知数;
(4)列:根据找出的(两个)相等关系列出所需的代数式,从而列出两个方程并组成方程组;
(5)解:解方程组;及检验.
(6)验:检验所得的解是不是方程组的解,并且要检验是否符合题意,不符合题意的要舍去;
(7)答:写出答案,包括单位名称.
2.当问题中所求的未知数有两个时,用两个字母来表示未知数往往比较容易列出方程.
【经典例题】
例题1、我国古代数学名著《孙子算经》中记载了一道数学趣题,这就是着名的“鸡兔同笼”问题.书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”意思就是:笼子里有若干只鸡和兔,从上面数,有35个头,从下面数,有94只脚,问鸡和兔各有多少只?
【考点】应用二元一次方程组解决实际问题.
【分析】根据题中的等量关系:鸡的只数+兔的只数=35头,所有鸡的脚数+所有兔的脚数=94只脚,列出方程组求解即可.
【解答】设鸡有x只,兔有y只.
根据题意,得
解方程组,得
答:鸡有23只,兔有12只.
【点评】列二元一次方程组解应用题,需要设两个未知数,找两个相等关系.
例题2、某学校的篮球数比排球数的2倍少3个,若篮球与排球分别被借出6个和4个,剩下的篮球和排球数的数量是学校篮球和排球总数的三分之一,设篮球有x个,排球与y个,根据题意列方程组为(
)
A.
B.
C.
D.
【考点】应用二元一次方程组解决实际问题.?
【分析】找准等量关系,正确列出二元一次方程组是解题的关键.
【解答】根据题意,得
故选B.
【点评】列二元一次方程组解决和、差、倍、分问题时,要抓住题目中反应数量关系的关键字(词);和、差、倍、几分之几、比、大、小、增加、减少等,列方程时,要明确关键字的含义,寻找等量关系,设出合适的未知数.
【夯实基础】
1.《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其中记载:今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?译文:今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又会差4钱,问人数、物价各是多少?设合伙人数为x人,物价为y钱,以下列出的方程组正确的是
A.
B.
C.
D..?
2.如图,
在大长方形ABCD中、放入七个相同的小长方形、BC=17、DE=7,则图中阴影部分的面积为(
)
A.57
B.67
C.77
D.87.?
3.一副三角板的放置如图所示,若∠2比∠1大10°,则所列方程组正确的是(?
)
A
.
??B
.??
C
.?
?D
.?
4.甲、乙两人练习跑步,如果甲让乙先跑10米,甲跑5秒钟就可追上乙,如果甲让乙先跑2秒钟,那么甲跑4秒钟就能追上乙,若设甲、乙每秒钟分别跑x,y米,列出方程组为(
)
A.
B.
C.
D.
5.在一个长方形中,若长减少3cm,宽加长5cm,面积不变;若长加长4cm,宽减少2cm,面积不变,则这个长方形的长为
cm,宽为
cm,面积为
cm2.
6.甲乙隔河放牧羊,两人相互问数量:甲说得乙羊九只,我羊是你羊二倍;乙说得甲羊八只,两人羊数正相当。请你帮忙算一算,甲放的羊数
,乙放的羊数
.
7.某体育活动中心购买了15个篮球和8个足球,一共花费了2051元,其中足球的单价比篮球的单价多12元,求篮球的单价和足球的单价.设篮球的单价为x元,足球的单价为y元,依题意,可列方程组为
.
8.某自行车行为提高市民的环保意识,倡导“节能减排,绿色出行”,计划在11月11日这天投放一批打折单车,这批单车分为A,B两种不同款型,其中A型车打七折后单价420元,B型车打八折后单价400元.计划打折A,B两种款型的单车共100辆,总共让利11600元.试问本次打折的A型车与B型车各多少辆?
9.已知8m·16n=128,与是同类项,求m、n的值.
【提优特训】
10.八年级1班36位同学在植树节这天共种了124棵树苗,其中男生每人种4棵,女生每人种3棵.则其中男生人数比女生人数多( )
A.
6人
B.
5人
C.
4人
D.
3人
11.某人有33枚1角与5角的硬币若干,共计是10元9角,其中1角与5角的硬币各是多少?设1角硬币x枚,5角硬币y枚,可方程组为(
)
A.
B.
C.
D.
12.已知14a7b=11+12c,9a12b12c=14,则a+b的值为(
).
A.3
B.4
C.5
D.6
13.在《九章算术》中记载一道这样的题:“今有甲、乙二人持钱不知其数,甲得乙半而钱
五十,乙得甲太半而亦钱五十,甲、乙持钱各几何?”题目大意是:甲、乙两人各带若干
钱,如果甲
得到乙所有钱的一半,那么甲共有钱50,如果乙得到甲所有钱的,那么乙
也共有钱50.甲、乙两人各需带多少钱?设甲需带钱x,乙带钱y,根据题意可列方程组
为( )
A.
B.
C.
D.
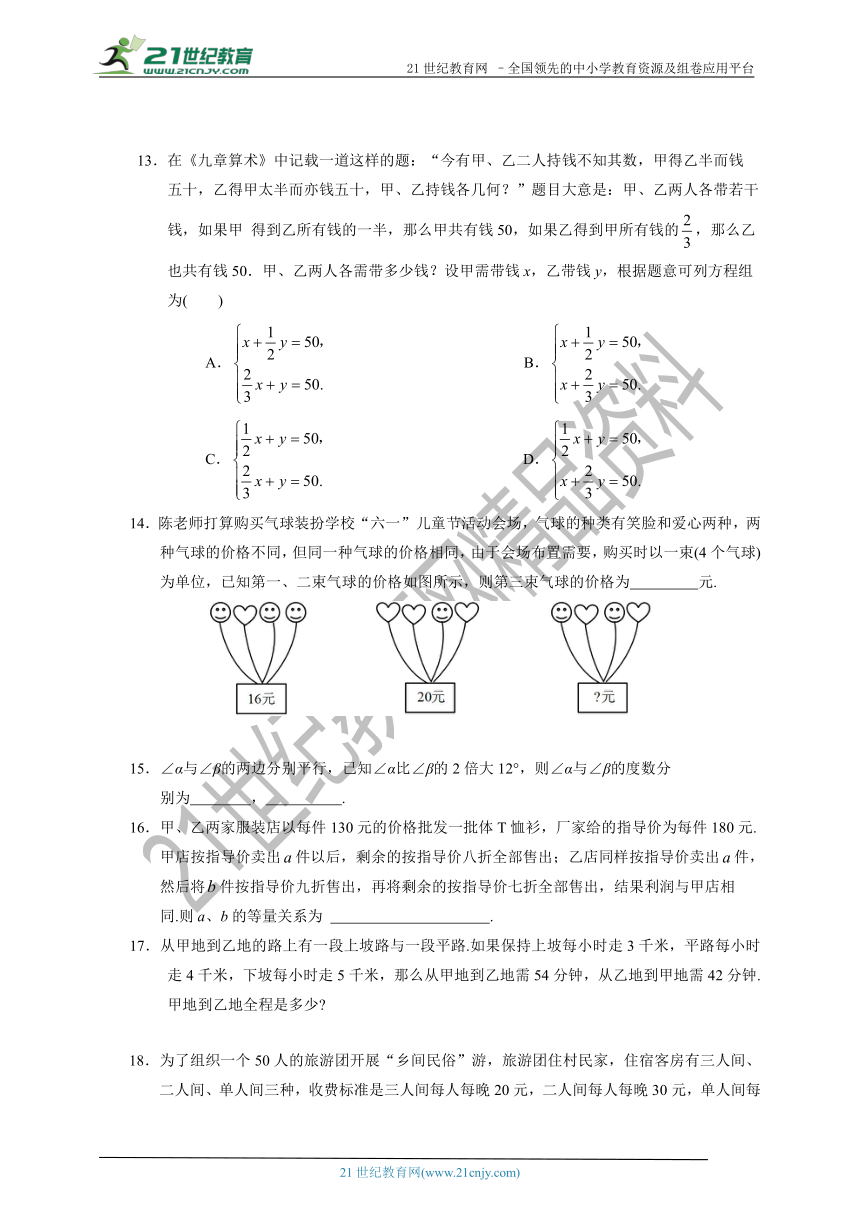
14.陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为
元.
15.∠α与∠β的两边分别平行,已知∠α比∠β的2倍大12°,则∠α与∠β的度数分
别为
,
.
16.甲、乙两家服装店以每件130元的价格批发一批体T恤衫,厂家给的指导价为每件180元.
甲店按指导价卖出件以后,剩余的按指导价八折全部售出;乙店同样按指导价卖出件,
然后将件按指导价九折售出,再将剩余的按指导价七折全部售出,结果利润与甲店相
同.则a、b的等量关系为
.
17.从甲地到乙地的路上有一段上坡路与一段平路.如果保持上坡每小时走3千米,平路每小时走4千米,下坡每小时走5千米,那么从甲地到乙地需54分钟,从乙地到甲地需42分钟.甲地到乙地全程是多少?
18.为了组织一个50人的旅游团开展“乡间民俗”游,旅游团住村民家,住宿客房有三人间、二人间、单人间三种,收费标准是三人间每人每晚20元,二人间每人每晚30元,单人间每人每晚50元,旅游团共住20间客房.若单人间住了4间,且恰好将20间客房住满,求三人间和二人间各入住多少间?
19.已知仙鹤和乌龟是动物中的长寿星,一天鹤父、鹤女与龟祖、龟孙在聊天,它们发现鹤父的年龄是鹤女的2倍,龟祖的年龄是龟孙的5倍,它们四位的年龄和的3倍恰好是900岁.十年后,鹤父和鹤女之和的5倍,加上龟祖、龟孙的年龄也是900岁,试求它们分别是多少岁?
20.亚洲文明对话会召开期间,大批的大学生志愿者参与范围工作.某大学计划组织本校全体
志愿者同一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若单独调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.求(1)计划调配
36座新能源客车多少辆?该大学共有多少名志愿者?(2)若同时调配36座和22座两种车型,既保证每人都有座,又保证每辆车不空座,则两种车型各多少辆?
【中考链接】
21.(2019?湖南长沙)
《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长、绳子还剩余4.5尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为x尺,绳子长为y尺,则所列方程组正确的是
A.
B.
C.
D.
22.(2019?安徽)
为实施乡村振兴战略,解决某山区老百姓出行难问题,当地政府决定修建一条高速公路,其中一段长146米的山体隧道贯穿工程由甲乙两个工程队负责施工,甲工程队独立工作2天后,乙工程队加入,两工程队又联合工作了1天,这3天共掘进26米,已知甲工程队每天比乙工程队多掘进2米,按此速度完成这项隧道贯穿工程,甲乙两个工程队还需要联合工作多少天?
23.(2019?湖南衡阳)
某班组织活动,班委会准备用15元钱全部用来购买笔记本和中性笔两种奖品.已知笔记本2元/本,中性笔1元/支,且每种奖品至少买一件.
(1)若设购买笔记本x本,中性笔y支,写出y与x之间的关系式;
(2)有多少种购买方案?请列举所有可能的结果;
参考答案
1、C
2、B
3、B
4、D
5、5、6、30
6、59、43
7、
10、D
11、A
12、C
13、A
14、18
15、124°、56°
16、a+2b=150
21.A
8.某自行车行为提高市民的环保意识,倡导“节能减排,绿色出行”,计划在11月11日这天投放一批打折单车,这批单车分为A,B两种不同款型,其中A型车打七折后单价420元,B型车打八折后单价400元.计划打折A,B两种款型的单车共100辆,总共让利11600元.试问本次打折的A型车与B型车各多少辆?
解:(1)设本次试点投放的A型车x辆、B型车y辆,
根据题意,得:,
解得:
答:本次打折的A型车20辆、B型车80辆.
9.已知8m·16n=128,与是同类项,求m、n的值.
解:∵8m·16n=128,
∴23m·24n=27,
∴23m+4n=27,
∴3m+4n=7,
∵与是同类项,
∴4n+m1=5m+1,
解方程组得
17.从甲地到乙地的路上有一段上坡路与一段平路.如果保持上坡每小时走3千米,平路每小时走4千米,下坡每小时走5千米,那么从甲地到乙地需54分钟,从乙地到甲地需42分钟.甲地到乙地全程是多少?
解:设从甲地到乙地的上坡路为xkm,平路为ykm,
根据题意,得:
解得:
所以:x+y=3.1千米
答:甲地到乙地的全程是3.1千米.
18.为了组织一个50人的旅游团开展“乡间民俗”游,旅游团住村民家,住宿客房有三人间、二人间、单人间三种,收费标准是三人间每人每晚20元,二人间每人每晚30元,单人间每人每晚50元,旅游团共住20间客房.若单人间住了4间,且恰好将20间客房住满,求三人间和二人间各入住多少间?
解:设三人间,二人间,单人间分别住了x,y间,其中x,y都是自然数,
则,
解得.
答:三人间住14间和二人间住2间.
19.已知仙鹤和乌龟是动物中的长寿星,一天鹤父、鹤女与龟祖、龟孙在聊天,它们发现鹤父的年龄是鹤女的2倍,龟祖的年龄是龟孙的5倍,它们四位的年龄和的3倍恰好是900岁.十年后,鹤父和鹤女之和的5倍,加上龟祖、龟孙的年龄也是900岁,试求它们分别是多少岁?
解:设鹤女x岁,鹤父2x,龟孙y,龟祖5y,
十年后鹤女x+10岁,鹤父2x+10,龟孙y+10,龟祖5y+10,
根据题意,
解得:
,
所以2x=80,5y=150,
答:鹤女40,鹤父80,龟孙30,龟祖150.
20.亚洲文明对话会召开期间,大批的大学生志愿者参与范围工作.某大学计划组织本校全体
志愿者同一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若单独调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.求(1)计划调配
36座新能源客车多少辆?该大学共有多少名志愿者?(2)若同时调配36座和22座两种车型,既保证每人都有座,又保证每辆车不空座,则两种车型各多少辆?
解:(1)设计划调配36座新能源客车x辆,该大学共有y名志愿者,则在调配22座新能源客车(x+4)辆,
根据题意,得
解得:
,
(2)设需调配36座客车m辆,22座客车n辆,
根据题意,得36m+22n=218,
又因为m、n均为正整数,
所以.
22.(2019?安徽)
为实施乡村振兴战略,解决某山区老百姓出行难问题,当地政府决定修建一条高速公路,其中一段长146米的山体隧道贯穿工程由甲乙两个工程队负责施工,甲工程队独立工作2天后,乙工程队加入,两工程队又联合工作了1天,这3天共掘进26米,已知甲工程队每天比乙工程队多掘进2米,按此速度完成这项隧道贯穿工程,甲乙两个工程队还需要联合工作多少天?
解:设甲工程队每天掘进x米,乙工程队每天掘进y米,
根据题意有:
解得
所以,(14626)÷(7+5)=10
答:甲乙两个工程队还需联合工作10天.
23.(2019?湖南衡阳)
某班组织活动,班委会准备用15元钱全部用来购买笔记本和中性笔两种奖品.已知笔记本2元/本,中性笔1元/支,且每种奖品至少买一件.
(1)若设购买笔记本x本,中性笔y支,写出y与x之间的关系式;
(2)有多少种购买方案?请列举所有可能的结果;
解:(1)∵由题意知2x+y=15,∴y与x之间的关系式为2x+y=15;
(2)∵在2x+y=15中,2x为偶数,15为奇数,∴y必为奇数,
∵每种奖品至少买一件,∴x≥1,y≥1,
∴奇数y只能取1、3、5、7、9、11、13这七个数
∴共有七种购买方案,如右图所示:
方
案
1
2
3
4
5
6
7
笔记本(本)
7
6
5
4
3
2
1
中性笔(支)
1
3
5
7
9
11
13
第2题图
第3题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
北师大版2020-2021学年度上学期八年级数学上册第五章二元一次方程组
5.3
应用二元一次方程组——鸡兔同笼
【知识清单】
1.
列方程组解决实际问题的一般步骤:
(1)审:认真审题,弄清问题中已知量和未知量;问题给出和涉及的相等关系是什么.
(2)找:找出问题给出和涉及的(两个)等量关系;
(3)设:(未知数).用字母表示题中的两个未知数;设未知数分为①直接未知数;②间接未知数;
(4)列:根据找出的(两个)相等关系列出所需的代数式,从而列出两个方程并组成方程组;
(5)解:解方程组;及检验.
(6)验:检验所得的解是不是方程组的解,并且要检验是否符合题意,不符合题意的要舍去;
(7)答:写出答案,包括单位名称.
2.当问题中所求的未知数有两个时,用两个字母来表示未知数往往比较容易列出方程.
【经典例题】
例题1、我国古代数学名著《孙子算经》中记载了一道数学趣题,这就是着名的“鸡兔同笼”问题.书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”意思就是:笼子里有若干只鸡和兔,从上面数,有35个头,从下面数,有94只脚,问鸡和兔各有多少只?
【考点】应用二元一次方程组解决实际问题.
【分析】根据题中的等量关系:鸡的只数+兔的只数=35头,所有鸡的脚数+所有兔的脚数=94只脚,列出方程组求解即可.
【解答】设鸡有x只,兔有y只.
根据题意,得
解方程组,得
答:鸡有23只,兔有12只.
【点评】列二元一次方程组解应用题,需要设两个未知数,找两个相等关系.
例题2、某学校的篮球数比排球数的2倍少3个,若篮球与排球分别被借出6个和4个,剩下的篮球和排球数的数量是学校篮球和排球总数的三分之一,设篮球有x个,排球与y个,根据题意列方程组为(
)
A.
B.
C.
D.
【考点】应用二元一次方程组解决实际问题.?
【分析】找准等量关系,正确列出二元一次方程组是解题的关键.
【解答】根据题意,得
故选B.
【点评】列二元一次方程组解决和、差、倍、分问题时,要抓住题目中反应数量关系的关键字(词);和、差、倍、几分之几、比、大、小、增加、减少等,列方程时,要明确关键字的含义,寻找等量关系,设出合适的未知数.
【夯实基础】
1.《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其中记载:今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?译文:今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又会差4钱,问人数、物价各是多少?设合伙人数为x人,物价为y钱,以下列出的方程组正确的是
A.
B.
C.
D..?
2.如图,
在大长方形ABCD中、放入七个相同的小长方形、BC=17、DE=7,则图中阴影部分的面积为(
)
A.57
B.67
C.77
D.87.?
3.一副三角板的放置如图所示,若∠2比∠1大10°,则所列方程组正确的是(?
)
A
.
??B
.??
C
.?
?D
.?
4.甲、乙两人练习跑步,如果甲让乙先跑10米,甲跑5秒钟就可追上乙,如果甲让乙先跑2秒钟,那么甲跑4秒钟就能追上乙,若设甲、乙每秒钟分别跑x,y米,列出方程组为(
)
A.
B.
C.
D.
5.在一个长方形中,若长减少3cm,宽加长5cm,面积不变;若长加长4cm,宽减少2cm,面积不变,则这个长方形的长为
cm,宽为
cm,面积为
cm2.
6.甲乙隔河放牧羊,两人相互问数量:甲说得乙羊九只,我羊是你羊二倍;乙说得甲羊八只,两人羊数正相当。请你帮忙算一算,甲放的羊数
,乙放的羊数
.
7.某体育活动中心购买了15个篮球和8个足球,一共花费了2051元,其中足球的单价比篮球的单价多12元,求篮球的单价和足球的单价.设篮球的单价为x元,足球的单价为y元,依题意,可列方程组为
.
8.某自行车行为提高市民的环保意识,倡导“节能减排,绿色出行”,计划在11月11日这天投放一批打折单车,这批单车分为A,B两种不同款型,其中A型车打七折后单价420元,B型车打八折后单价400元.计划打折A,B两种款型的单车共100辆,总共让利11600元.试问本次打折的A型车与B型车各多少辆?
9.已知8m·16n=128,与是同类项,求m、n的值.
【提优特训】
10.八年级1班36位同学在植树节这天共种了124棵树苗,其中男生每人种4棵,女生每人种3棵.则其中男生人数比女生人数多( )
A.
6人
B.
5人
C.
4人
D.
3人
11.某人有33枚1角与5角的硬币若干,共计是10元9角,其中1角与5角的硬币各是多少?设1角硬币x枚,5角硬币y枚,可方程组为(
)
A.
B.
C.
D.
12.已知14a7b=11+12c,9a12b12c=14,则a+b的值为(
).
A.3
B.4
C.5
D.6
13.在《九章算术》中记载一道这样的题:“今有甲、乙二人持钱不知其数,甲得乙半而钱
五十,乙得甲太半而亦钱五十,甲、乙持钱各几何?”题目大意是:甲、乙两人各带若干
钱,如果甲
得到乙所有钱的一半,那么甲共有钱50,如果乙得到甲所有钱的,那么乙
也共有钱50.甲、乙两人各需带多少钱?设甲需带钱x,乙带钱y,根据题意可列方程组
为( )
A.
B.
C.
D.
14.陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为
元.
15.∠α与∠β的两边分别平行,已知∠α比∠β的2倍大12°,则∠α与∠β的度数分
别为
,
.
16.甲、乙两家服装店以每件130元的价格批发一批体T恤衫,厂家给的指导价为每件180元.
甲店按指导价卖出件以后,剩余的按指导价八折全部售出;乙店同样按指导价卖出件,
然后将件按指导价九折售出,再将剩余的按指导价七折全部售出,结果利润与甲店相
同.则a、b的等量关系为
.
17.从甲地到乙地的路上有一段上坡路与一段平路.如果保持上坡每小时走3千米,平路每小时走4千米,下坡每小时走5千米,那么从甲地到乙地需54分钟,从乙地到甲地需42分钟.甲地到乙地全程是多少?
18.为了组织一个50人的旅游团开展“乡间民俗”游,旅游团住村民家,住宿客房有三人间、二人间、单人间三种,收费标准是三人间每人每晚20元,二人间每人每晚30元,单人间每人每晚50元,旅游团共住20间客房.若单人间住了4间,且恰好将20间客房住满,求三人间和二人间各入住多少间?
19.已知仙鹤和乌龟是动物中的长寿星,一天鹤父、鹤女与龟祖、龟孙在聊天,它们发现鹤父的年龄是鹤女的2倍,龟祖的年龄是龟孙的5倍,它们四位的年龄和的3倍恰好是900岁.十年后,鹤父和鹤女之和的5倍,加上龟祖、龟孙的年龄也是900岁,试求它们分别是多少岁?
20.亚洲文明对话会召开期间,大批的大学生志愿者参与范围工作.某大学计划组织本校全体
志愿者同一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若单独调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.求(1)计划调配
36座新能源客车多少辆?该大学共有多少名志愿者?(2)若同时调配36座和22座两种车型,既保证每人都有座,又保证每辆车不空座,则两种车型各多少辆?
【中考链接】
21.(2019?湖南长沙)
《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长、绳子还剩余4.5尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为x尺,绳子长为y尺,则所列方程组正确的是
A.
B.
C.
D.
22.(2019?安徽)
为实施乡村振兴战略,解决某山区老百姓出行难问题,当地政府决定修建一条高速公路,其中一段长146米的山体隧道贯穿工程由甲乙两个工程队负责施工,甲工程队独立工作2天后,乙工程队加入,两工程队又联合工作了1天,这3天共掘进26米,已知甲工程队每天比乙工程队多掘进2米,按此速度完成这项隧道贯穿工程,甲乙两个工程队还需要联合工作多少天?
23.(2019?湖南衡阳)
某班组织活动,班委会准备用15元钱全部用来购买笔记本和中性笔两种奖品.已知笔记本2元/本,中性笔1元/支,且每种奖品至少买一件.
(1)若设购买笔记本x本,中性笔y支,写出y与x之间的关系式;
(2)有多少种购买方案?请列举所有可能的结果;
参考答案
1、C
2、B
3、B
4、D
5、5、6、30
6、59、43
7、
10、D
11、A
12、C
13、A
14、18
15、124°、56°
16、a+2b=150
21.A
8.某自行车行为提高市民的环保意识,倡导“节能减排,绿色出行”,计划在11月11日这天投放一批打折单车,这批单车分为A,B两种不同款型,其中A型车打七折后单价420元,B型车打八折后单价400元.计划打折A,B两种款型的单车共100辆,总共让利11600元.试问本次打折的A型车与B型车各多少辆?
解:(1)设本次试点投放的A型车x辆、B型车y辆,
根据题意,得:,
解得:
答:本次打折的A型车20辆、B型车80辆.
9.已知8m·16n=128,与是同类项,求m、n的值.
解:∵8m·16n=128,
∴23m·24n=27,
∴23m+4n=27,
∴3m+4n=7,
∵与是同类项,
∴4n+m1=5m+1,
解方程组得
17.从甲地到乙地的路上有一段上坡路与一段平路.如果保持上坡每小时走3千米,平路每小时走4千米,下坡每小时走5千米,那么从甲地到乙地需54分钟,从乙地到甲地需42分钟.甲地到乙地全程是多少?
解:设从甲地到乙地的上坡路为xkm,平路为ykm,
根据题意,得:
解得:
所以:x+y=3.1千米
答:甲地到乙地的全程是3.1千米.
18.为了组织一个50人的旅游团开展“乡间民俗”游,旅游团住村民家,住宿客房有三人间、二人间、单人间三种,收费标准是三人间每人每晚20元,二人间每人每晚30元,单人间每人每晚50元,旅游团共住20间客房.若单人间住了4间,且恰好将20间客房住满,求三人间和二人间各入住多少间?
解:设三人间,二人间,单人间分别住了x,y间,其中x,y都是自然数,
则,
解得.
答:三人间住14间和二人间住2间.
19.已知仙鹤和乌龟是动物中的长寿星,一天鹤父、鹤女与龟祖、龟孙在聊天,它们发现鹤父的年龄是鹤女的2倍,龟祖的年龄是龟孙的5倍,它们四位的年龄和的3倍恰好是900岁.十年后,鹤父和鹤女之和的5倍,加上龟祖、龟孙的年龄也是900岁,试求它们分别是多少岁?
解:设鹤女x岁,鹤父2x,龟孙y,龟祖5y,
十年后鹤女x+10岁,鹤父2x+10,龟孙y+10,龟祖5y+10,
根据题意,
解得:
,
所以2x=80,5y=150,
答:鹤女40,鹤父80,龟孙30,龟祖150.
20.亚洲文明对话会召开期间,大批的大学生志愿者参与范围工作.某大学计划组织本校全体
志愿者同一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若单独调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.求(1)计划调配
36座新能源客车多少辆?该大学共有多少名志愿者?(2)若同时调配36座和22座两种车型,既保证每人都有座,又保证每辆车不空座,则两种车型各多少辆?
解:(1)设计划调配36座新能源客车x辆,该大学共有y名志愿者,则在调配22座新能源客车(x+4)辆,
根据题意,得
解得:
,
(2)设需调配36座客车m辆,22座客车n辆,
根据题意,得36m+22n=218,
又因为m、n均为正整数,
所以.
22.(2019?安徽)
为实施乡村振兴战略,解决某山区老百姓出行难问题,当地政府决定修建一条高速公路,其中一段长146米的山体隧道贯穿工程由甲乙两个工程队负责施工,甲工程队独立工作2天后,乙工程队加入,两工程队又联合工作了1天,这3天共掘进26米,已知甲工程队每天比乙工程队多掘进2米,按此速度完成这项隧道贯穿工程,甲乙两个工程队还需要联合工作多少天?
解:设甲工程队每天掘进x米,乙工程队每天掘进y米,
根据题意有:
解得
所以,(14626)÷(7+5)=10
答:甲乙两个工程队还需联合工作10天.
23.(2019?湖南衡阳)
某班组织活动,班委会准备用15元钱全部用来购买笔记本和中性笔两种奖品.已知笔记本2元/本,中性笔1元/支,且每种奖品至少买一件.
(1)若设购买笔记本x本,中性笔y支,写出y与x之间的关系式;
(2)有多少种购买方案?请列举所有可能的结果;
解:(1)∵由题意知2x+y=15,∴y与x之间的关系式为2x+y=15;
(2)∵在2x+y=15中,2x为偶数,15为奇数,∴y必为奇数,
∵每种奖品至少买一件,∴x≥1,y≥1,
∴奇数y只能取1、3、5、7、9、11、13这七个数
∴共有七种购买方案,如右图所示:
方
案
1
2
3
4
5
6
7
笔记本(本)
7
6
5
4
3
2
1
中性笔(支)
1
3
5
7
9
11
13
第2题图
第3题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
