沪科版(2012)初中数学八年级上册13.1三角形中三边关系导学案(无答案)
文档属性
| 名称 | 沪科版(2012)初中数学八年级上册13.1三角形中三边关系导学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 43.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-15 20:35:48 | ||
图片预览

文档简介
13.1.1
三角形中三边关系
导学案
学习目标
1.了解三角形的概念,掌握分类讨论思想;
2.经历探索三角形中的三边关系,体会数形结合思想;
3.学会利用三角形三边关系解决简单的实际问题,体会数学的应用价值.
学习重难点
重点:了解三角形的分类,弄清三角形三边关系.
难点:利用三角形三边关系解决简单的实际问题.
一、自主学习
阅读课本P67内容,完成以下填空:
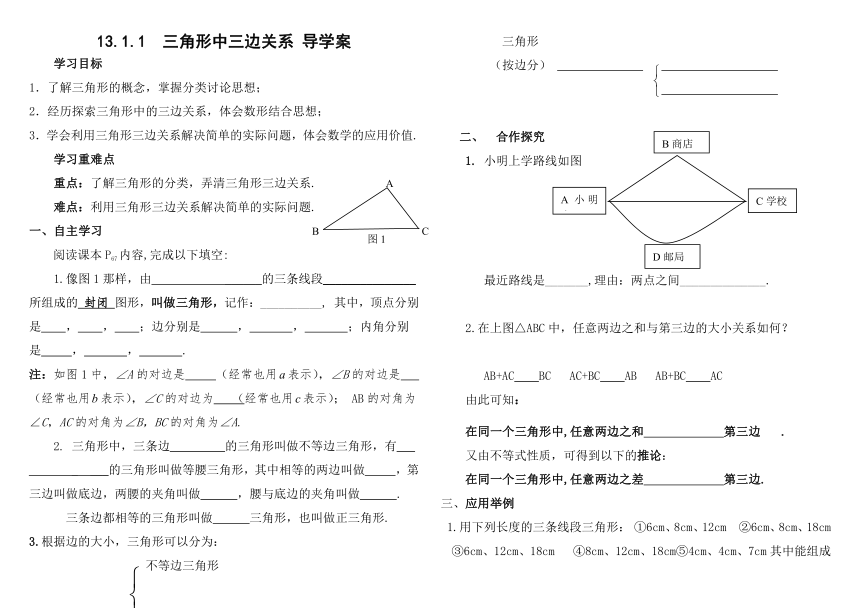
1.像图1那样,由
______的三条线段_______________所组成的
封闭
图形,叫做三角形,记作:__________,
其中,顶点分别是
,
,
;边分别是
,
,
;内角分别是
,
,
.
注:如图1中,∠A的对边是
(经常也用表示),∠B的对边是
(经常也用表示),∠C的对边为
(经常也用表示);
AB的对角为∠C,AC的对角为∠B,BC的对角为∠A.
2.
三角形中,三条边
的三角形叫做不等边三角形,有
_
___的三角形叫做等腰三角形,其中相等的两边叫做
,第三边叫做底边,两腰的夹角叫做
,腰与底边的夹角叫做
.
三条边都相等的三角形叫做
三角形,也叫做正三角形.
3.根据边的大小,三角形可以分为:
不等边三角形
三角形
(按边分)
2、
合作探究
1.
小明上学路线如图
最近路线是_______,理由:两点之间______________.
2.在上图△ABC中,任意两边之和与第三边的大小关系如何?
AB+AC
BC
AC+BC
AB
AB+BC
AC
由此可知:
在同一个三角形中,任意两边之和
第三边.
又由不等式性质,可得到以下的推论:
在同一个三角形中,任意两边之差
第三边.
三、应用举例
1.用下列长度的三条线段三角形:
①6cm、8cm、12cm
②6cm、8cm、18cm
③6cm、12cm、18cm
④8cm、12cm、18cm⑤4cm、4cm、7cm其中能组成三角形的是_________,不能组成三角形的是_________.(填写序号)
2.已知一个三角形的两条边长分别为3cm和9cm,则三角形第三条边长X的取值范围是_____________________.
3.(课本例1)(研读例题,不要求写出解题过程,只要求弄清例题的解题思路)
等腰三角形中,周长为18cm.
(1)如果腰长是底边长的2倍,求各边长.
(2)如果一边长为4cm,求另两边长.
思考:
问题(1)中,设___为_____
cm,利用___________等量关系列方程求解.
问题(2)中,长为4cm的边是指底边还是腰?由此你应分几种情况来讨论?得到的每组数据都能组成三角形吗?根据讨论结果,你是否理解例题的解法?
4、
达标检测
1.下列长度的三条线段能否组成三角形?
(A)8,3,6
(
)
(B)2,5,8
(
)
(C)5,10,3(
)
(D)3,5,10
(
)
2.⑴已知等腰三角形的一边等于6,一边等于13,则它的周长为
.
⑵等腰三角形的两边长分别是7cm,8cm.求这个三角形的周长.
四、课堂小结
在这节课上,你学到了哪些知识?本节课运用了哪种数学思想方法?
五、课后作业
课本P69练习1、2、3
图1
A
B
C
B商店
A小明家
C学校
D邮局
三角形中三边关系
导学案
学习目标
1.了解三角形的概念,掌握分类讨论思想;
2.经历探索三角形中的三边关系,体会数形结合思想;
3.学会利用三角形三边关系解决简单的实际问题,体会数学的应用价值.
学习重难点
重点:了解三角形的分类,弄清三角形三边关系.
难点:利用三角形三边关系解决简单的实际问题.
一、自主学习
阅读课本P67内容,完成以下填空:
1.像图1那样,由
______的三条线段_______________所组成的
封闭
图形,叫做三角形,记作:__________,
其中,顶点分别是
,
,
;边分别是
,
,
;内角分别是
,
,
.
注:如图1中,∠A的对边是
(经常也用表示),∠B的对边是
(经常也用表示),∠C的对边为
(经常也用表示);
AB的对角为∠C,AC的对角为∠B,BC的对角为∠A.
2.
三角形中,三条边
的三角形叫做不等边三角形,有
_
___的三角形叫做等腰三角形,其中相等的两边叫做
,第三边叫做底边,两腰的夹角叫做
,腰与底边的夹角叫做
.
三条边都相等的三角形叫做
三角形,也叫做正三角形.
3.根据边的大小,三角形可以分为:
不等边三角形
三角形
(按边分)
2、
合作探究
1.
小明上学路线如图
最近路线是_______,理由:两点之间______________.
2.在上图△ABC中,任意两边之和与第三边的大小关系如何?
AB+AC
BC
AC+BC
AB
AB+BC
AC
由此可知:
在同一个三角形中,任意两边之和
第三边.
又由不等式性质,可得到以下的推论:
在同一个三角形中,任意两边之差
第三边.
三、应用举例
1.用下列长度的三条线段三角形:
①6cm、8cm、12cm
②6cm、8cm、18cm
③6cm、12cm、18cm
④8cm、12cm、18cm⑤4cm、4cm、7cm其中能组成三角形的是_________,不能组成三角形的是_________.(填写序号)
2.已知一个三角形的两条边长分别为3cm和9cm,则三角形第三条边长X的取值范围是_____________________.
3.(课本例1)(研读例题,不要求写出解题过程,只要求弄清例题的解题思路)
等腰三角形中,周长为18cm.
(1)如果腰长是底边长的2倍,求各边长.
(2)如果一边长为4cm,求另两边长.
思考:
问题(1)中,设___为_____
cm,利用___________等量关系列方程求解.
问题(2)中,长为4cm的边是指底边还是腰?由此你应分几种情况来讨论?得到的每组数据都能组成三角形吗?根据讨论结果,你是否理解例题的解法?
4、
达标检测
1.下列长度的三条线段能否组成三角形?
(A)8,3,6
(
)
(B)2,5,8
(
)
(C)5,10,3(
)
(D)3,5,10
(
)
2.⑴已知等腰三角形的一边等于6,一边等于13,则它的周长为
.
⑵等腰三角形的两边长分别是7cm,8cm.求这个三角形的周长.
四、课堂小结
在这节课上,你学到了哪些知识?本节课运用了哪种数学思想方法?
五、课后作业
课本P69练习1、2、3
图1
A
B
C
B商店
A小明家
C学校
D邮局
