鲁教 版(五四制)八年级上册《第5章 平行四边形》 单元测试卷(Word版 含解析)
文档属性
| 名称 | 鲁教 版(五四制)八年级上册《第5章 平行四边形》 单元测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 311.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-14 19:06:31 | ||
图片预览

文档简介
第5章
平行四边形
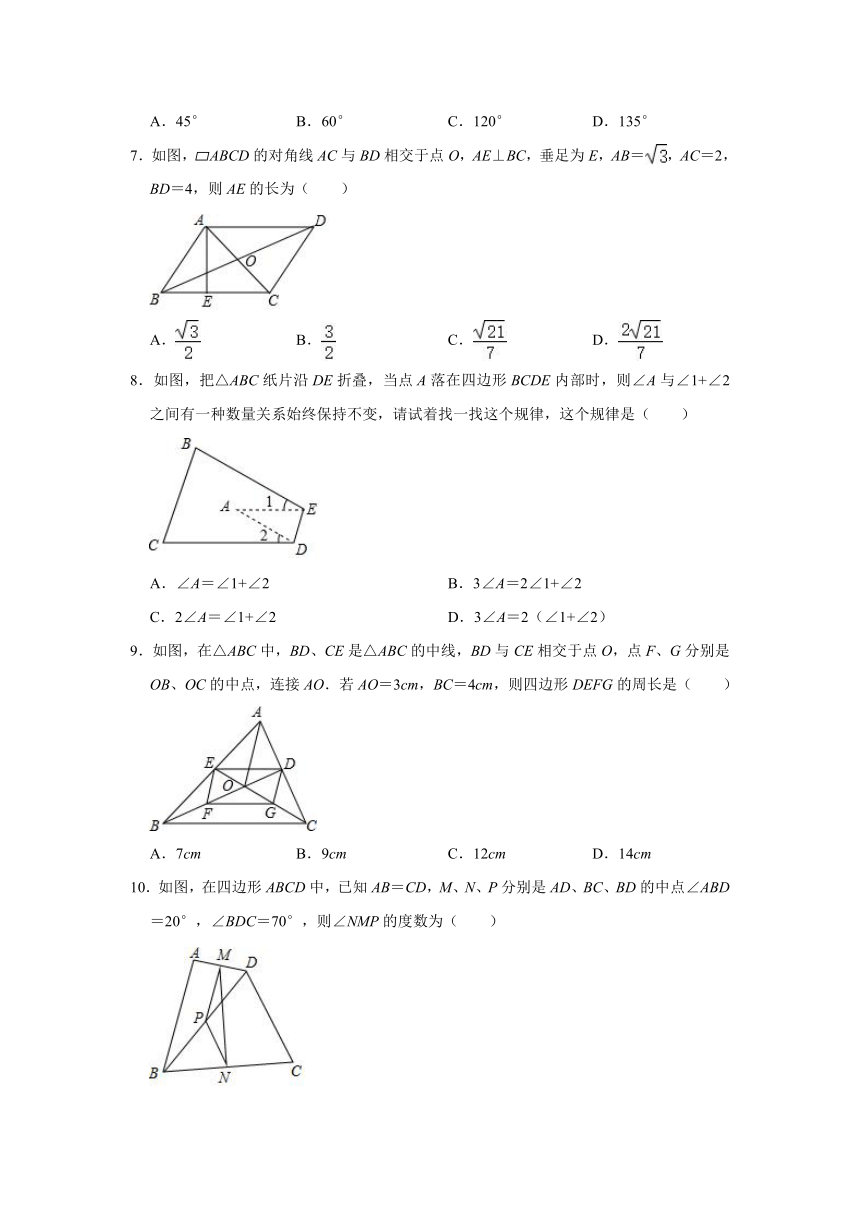
一、选择题(共12小题,每小题3分,共36分)
1.已知四边形ABCD,有以下四个条件:
(1)AB=AD,AB=BC;(2)∠A=∠B,∠C=∠D;(3)AB∥CD,AB=CD;(4)AB∥CD,AD∥BC.
其中能判定四边形ABCD是平行四边形的有( )个.
A.1
B.2
C.3
D.4
2.平行四边形一边的长是10cm,那么这个平行四边形的两条对角线长可以是( )
A.4cm,6cm
B.6cm,8cm
C.8cm,12cm
D.20cm,30cm
3.如图所示,?ABCD的对角线AC,BD相交于点O,AE=EB,OE=3,AB=5,?ABCD的周长( )
A.11
B.13
C.16
D.22
4.如图,?ABCD的对角线AC,BD交于点O,AC⊥AB,AB=,且AC:BD=2:3,那么AC的长为( )
A.2
B.
C.3
D.4
5.如图,在?ABCD中,AB=3,AD=5,∠BCD的平分线交BA的延长线于点E,则AE的长为( )
A.3
B.2.5
C.2
D.1.5
6.如果一个正多边形内角和等于1080°,那么这个正多边形的每一个外角等于( )
A.45°
B.60°
C.120°
D.135°
7.如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=,AC=2,BD=4,则AE的长为( )
A.
B.
C.
D.
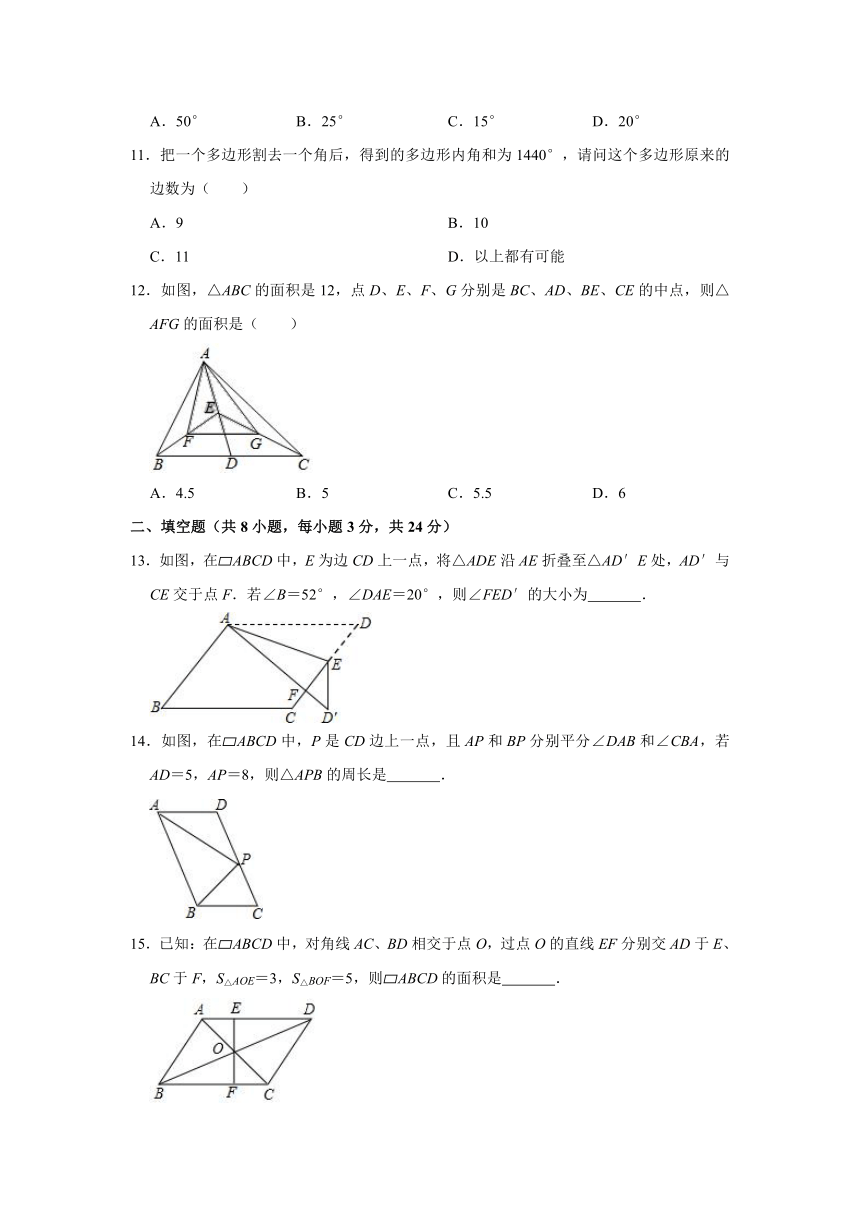
8.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
A.∠A=∠1+∠2
B.3∠A=2∠1+∠2
C.2∠A=∠1+∠2
D.3∠A=2(∠1+∠2)
9.如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点O,点F、G分别是OB、OC的中点,连接AO.若AO=3cm,BC=4cm,则四边形DEFG的周长是( )
A.7cm
B.9cm
C.12cm
D.14cm
10.如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD的中点∠ABD=20°,∠BDC=70°,则∠NMP的度数为( )
A.50°
B.25°
C.15°
D.20°
11.把一个多边形割去一个角后,得到的多边形内角和为1440°,请问这个多边形原来的边数为( )
A.9
B.10
C.11
D.以上都有可能
12.如图,△ABC的面积是12,点D、E、F、G分别是BC、AD、BE、CE的中点,则△AFG的面积是( )
A.4.5
B.5
C.5.5
D.6
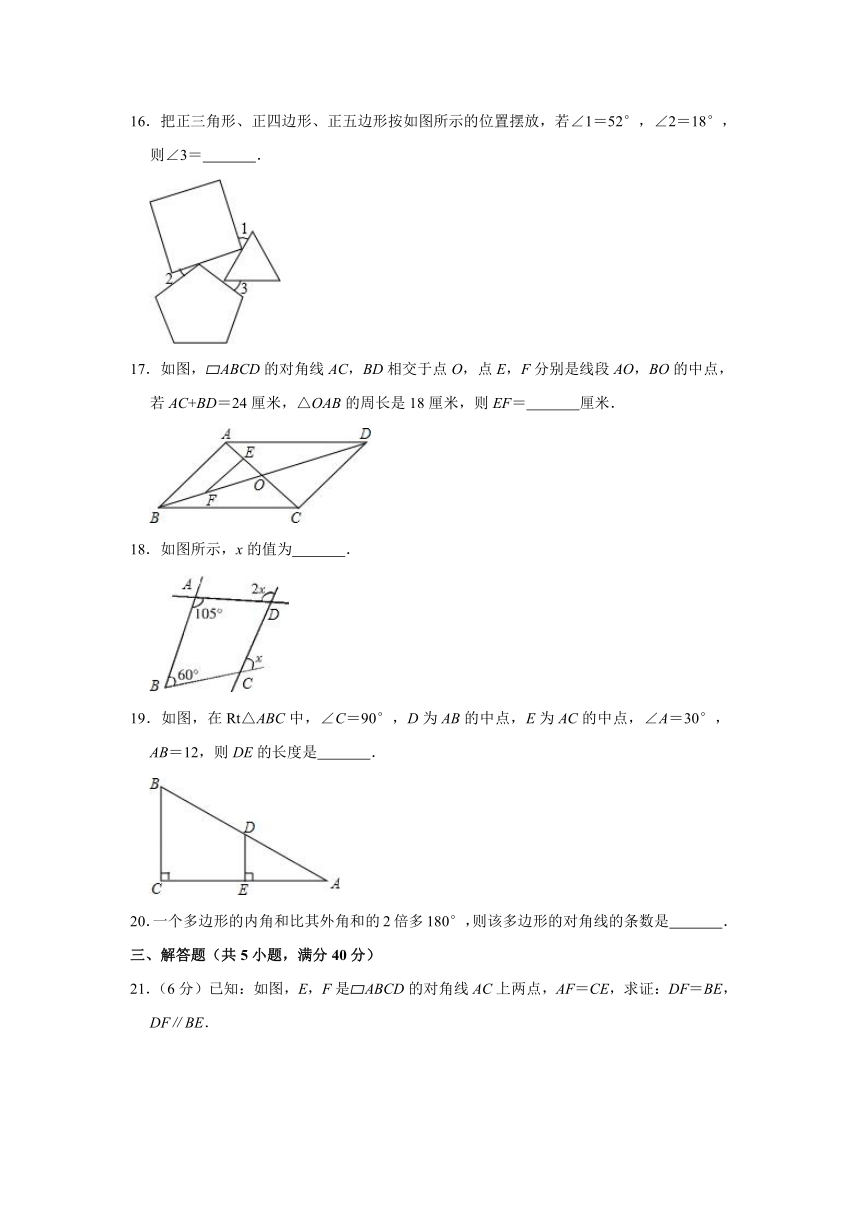
二、填空题(共8小题,每小题3分,共24分)
13.如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为
.
14.如图,在?ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是
.
15.已知:在?ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AD于E、BC于F,S△AOE=3,S△BOF=5,则?ABCD的面积是
.
16.把正三角形、正四边形、正五边形按如图所示的位置摆放,若∠1=52°,∠2=18°,则∠3=
.
17.如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=
厘米.
18.如图所示,x的值为
.
19.如图,在Rt△ABC中,∠C=90°,D为AB的中点,E为AC的中点,∠A=30°,AB=12,则DE的长度是
.
20.一个多边形的内角和比其外角和的2倍多180°,则该多边形的对角线的条数是
.
三、解答题(共5小题,满分40分)
21.(6分)已知:如图,E,F是?ABCD的对角线AC上两点,AF=CE,求证:DF=BE,DF∥BE.
22.(8分)已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC
边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
23.(8分)如图,△ABC中,BC>AC,点D在BC上,且CA=CD,∠ACB的平分线交AD于点F,E是AB的中点.
(1)求证:EF∥BD;
(2)若∠ACB=60°,AC=8,BC=12,求四边形BDFE的面积.
24.(9分)如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
25.(9分)如图所示,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P从A向点D以1cm/s的速度运动,到点D即停止.点Q从点C向点B以2cm/s的速度运动,到点B即停止.直线PQ将四边形ABCD截得两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形?
参考答案与试题解析
一、选择题(共12小题,每小题3分,共36分)
1.已知四边形ABCD,有以下四个条件:
(1)AB=AD,AB=BC;(2)∠A=∠B,∠C=∠D;(3)AB∥CD,AB=CD;(4)AB∥CD,AD∥BC.
其中能判定四边形ABCD是平行四边形的有( )个.
A.1
B.2
C.3
D.4
【分析】平行四边形的判定:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形.
【解答】解:根据平行四边形的判定定理知,(1),(2)不符合是平行四边形的条件;
(3)(4)满足四边形是平行四边形.
故选:B.
2.平行四边形一边的长是10cm,那么这个平行四边形的两条对角线长可以是( )
A.4cm,6cm
B.6cm,8cm
C.8cm,12cm
D.20cm,30cm
【分析】平行四边形的这条边和两条对角线的一半构成三角形,应该满足第三边大于两边之差小于两边之和才能构成三角形.
【解答】解:A、∵2+3<10,不能够成三角形,故此选项错误;
B、4+3<10,不能够成三角形,故此选项错误;
C、4+6=10,不能构成三角形,故此选项错误;
D、10+10>15,能够成三角形,故此选项正确;
故选:D.
3.如图所示,?ABCD的对角线AC,BD相交于点O,AE=EB,OE=3,AB=5,?ABCD的周长( )
A.11
B.13
C.16
D.22
【分析】由?ABCD的对角线AC,BD相交于点O,AE=EB,易得DE是△ABC的中位线,即可求得BC的长,继而求得答案.
【解答】解:∵?ABCD的对角线AC,BD相交于点O,
∴OA=OC,AD=BC,AB=CD=5,
∵AE=EB,OE=3,
∴BC=2OE=6,
∴?ABCD的周长=2×(AB+BC)=22.
故选:D.
4.如图,?ABCD的对角线AC,BD交于点O,AC⊥AB,AB=,且AC:BD=2:3,那么AC的长为( )
A.2
B.
C.3
D.4
【分析】根据平行四边形的性质可知,OA=OC,OB=OD,由AC:BD=2:3,推出OA:OB=2:3,设OA=2m,OB=3m,在Rt△AOB中利用勾股定理即可解决问题.
【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AC:BD=2:3,
∴OA:OB=2:3,设OA=2m,BO=3m,
∵AC⊥BD,
∴∠BAO=90°,
∴OB2=AB2+OA2,
∴9m2=5+4m2,
∴m=±1,
∵m>0,
∴m=1,
∴AC=2OA=4.
故选:D.
5.如图,在?ABCD中,AB=3,AD=5,∠BCD的平分线交BA的延长线于点E,则AE的长为( )
A.3
B.2.5
C.2
D.1.5
【分析】由平行四边形ABCD中,CE平分∠BCD,可证得△BCE是等腰三角形,继而利用AE=BE﹣AB,求得答案.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=5,
∴∠E=∠ECD,
∵CE平分∠BCD,
∴∠BCE=∠ECD,
∴∠E=∠BCE,
∴BE=BC=5,
∴AE=BE﹣AB=5﹣3=2;故选:C.
6.如果一个正多边形内角和等于1080°,那么这个正多边形的每一个外角等于( )
A.45°
B.60°
C.120°
D.135°
【分析】首先设此多边形为n边形,根据题意得:180(n﹣2)=1080,即可求得n=8,再由多边形的外角和等于360°,即可求得答案.
【解答】解:设此多边形为n边形,
根据题意得:180(n﹣2)=1080,
解得:n=8,
∴这个正多边形的每一个外角等于:360°÷8=45°.
故选:A.
7.如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=,AC=2,BD=4,则AE的长为( )
A.
B.
C.
D.
【分析】由勾股定理的逆定理可判定△BAO是直角三角形,所以平行四边形ABCD的面积即可求出.
【解答】解:∵AC=2,BD=4,四边形ABCD是平行四边形,
∴AO=AC=1,BO=BD=2,
∵AB=,
∴AB2+AO2=BO2,
∴∠BAC=90°,
∵在Rt△BAC中,BC===
S△BAC=×AB×AC=×BC×AE,
∴×2=AE,
∴AE=,
故选:D.
8.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
A.∠A=∠1+∠2
B.3∠A=2∠1+∠2
C.2∠A=∠1+∠2
D.3∠A=2(∠1+∠2)
【分析】根据三角形的内角和定理,以及四边形的内角和定理即可求出答案.
【解答】解:由题意可知:∠AED+∠ADE=180°﹣∠A,
∠B+∠C=180°﹣∠A
∵∠AED+∠ADE+∠1+∠2+∠B+∠C=360°,
∴360°﹣2∠A+∠1+∠2=360°,
∴2∠A=∠1+∠2,
故选:C.
9.如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点O,点F、G分别是OB、OC的中点,连接AO.若AO=3cm,BC=4cm,则四边形DEFG的周长是( )
A.7cm
B.9cm
C.12cm
D.14cm
【分析】根据三角形中位线定理分别求出DE、EF、FG、DG,计算即可.
【解答】解:∵BD、CE是△ABC的中线,
∴DE=BC=2,
同理,FG=BC=2,EF=OA=1.5,DG=OA=1.5,
∴四边形DEFG的周长=DE+EF+FG+DG=7(cm),
故选:A.
10.如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD的中点∠ABD=20°,∠BDC=70°,则∠NMP的度数为( )
A.50°
B.25°
C.15°
D.20°
【分析】根据中位线定理和已知,易证明△PMN是等腰三角形,根据等腰三角形的性质和已知条件即可求出∠PMN的度数.
【解答】解:∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线,
∴PM=AB,PN=DC,PM∥AB,PN∥DC,
∵AB=CD,
∴PM=PN,
∴△PMN是等腰三角形,
∵PM∥AB,PN∥DC,
∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°,
∴∠MPN=∠MPD+∠NPD=20°+(180﹣70)°=130°,
∴∠PMN==25°.
故选:B.
11.把一个多边形割去一个角后,得到的多边形内角和为1440°,请问这个多边形原来的边数为( )
A.9
B.10
C.11
D.以上都有可能
【分析】先根据多边形的内角和公式(n﹣2)?180°求出截去一个角后的多边形的边数,再根据截去一个角后边数增加1,不变,减少1讨论得解.
【解答】解:设多边形截去一个角的边数为n,
则(n﹣2)?180°=1440°,
解得n=10,
∵截去一个角后边上可以增加1,不变,减少1,
∴原多边形的边数是9或10或11.
故选:D.
12.如图,△ABC的面积是12,点D、E、F、G分别是BC、AD、BE、CE的中点,则△AFG的面积是( )
A.4.5
B.5
C.5.5
D.6
【分析】根据中线的性质,可得△AEF的面积=×△ABE的面积=×△ABD的面积=×△ABC的面积=,△AEG的面积=,根据三角形中位线的性质可得△EFG的面积=×△BCE的面积=,进而得到△AFG的面积.
【解答】解:∵点D,E,F,G分别是BC,AD,BE,CE的中点,
∴AD是△ABC的中线,BE是△ABD的中线,CE是△ACD的中线,AF是△ABE的中线,AG是△ACE的中线,
∴△AEF的面积=×△ABE的面积=×△ABD的面积=×△ABC的面积=,
同理可得△AEG的面积=,
△BCE的面积=×△ABC的面积=6,
又∵FG是△BCE的中位线,
∴△EFG的面积=×△BCE的面积=,
∴△AFG的面积是×3=,
故选:A.
二、填空题(共8小题,每小题3分,共24分)
13.如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 36° .
【分析】由平行四边形的性质得出∠D=∠B=52°,由折叠的性质得:∠D′=∠D=52°,∠EAD′=∠DAE=20°,由三角形的外角性质求出∠AEF=72°,与三角形内角和定理求出∠AED′=108°,即可得出∠FED′的大小.
【解答】解:∵四边形ABCD是平行四边形,
∴∠D=∠B=52°,
由折叠的性质得:∠D′=∠D=52°,∠EAD′=∠DAE=20°,
∴∠AEF=∠D+∠DAE=52°+20°=72°,∠AED′=180°﹣∠EAD′﹣∠D′=108°,
∴∠FED′=108°﹣72°=36°;
故答案为:36°.
14.如图,在?ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是 24 .
【分析】根据平行四边形性质得出AD∥CB,AB∥CD,推出∠DAB+∠CBA=180°,求出∠PAB+∠PBA=90°,在△APB中求出∠APB=90°,由勾股定理求出BP,证出AD=DP=5,BC=PC=5,得出DC=10=AB,即可求出答案.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°﹣(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=5,
同理:PC=CB=5,
即AB=DC=DP+PC=10,
在Rt△APB中,AB=10,AP=8,
∴BP==6,
∴△APB的周长=6+8+10=24;
故答案为:24.
15.已知:在?ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AD于E、BC于F,S△AOE=3,S△BOF=5,则?ABCD的面积是 32 .
【分析】利用平行四边形的性质可证明△AOE≌△COF,所以可得△COF的面积为3,进而可得△BOC的面积为8,又因为△BOC的面积=?ABCD的面积,进而可得问题答案.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠FCO=∠EAC,
又∵AO=CO,∠AOE=∠COF,
∴△AOE≌△COF
∴△COF的面积为3,
∵S△BOF=5,
∴△BOC的面积为8,
∵△BOC的面积=?ABCD的面积,
∴?ABCD的面积=4×8=32,
故答案为:32.
16.把正三角形、正四边形、正五边形按如图所示的位置摆放,若∠1=52°,∠2=18°,则∠3= 32° .
【分析】利用360°减去等边三角形的一个内角的度数,减去正方形的一个内角的度数,减去正五边形的一个内角的度数,然后减去∠1和∠2即可求得.
【解答】解:等边三角形的内角的度数是60°,正方形的内角度数是90°,正五边形的内角的度数是:(5﹣2)×180°=108°,
则∠3=360°﹣60°﹣90°﹣108°﹣∠1﹣∠2=32°.
故答案是:32°.
17.如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF= 3 厘米.
【分析】根据AC+BD=24厘米,可得出出OA+OB=12cm,继而求出AB,判断EF是△OAB的中位线即可得出EF的长度.
【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵AC+BD=24厘米,
∴OA+OB=12cm,
∵△OAB的周长是18厘米,
∴AB=6cm,
∵点E,F分别是线段AO,BO的中点,
∴EF是△OAB的中位线,
∴EF=AB=3cm.
故答案为:3.
18.如图所示,x的值为 55° .
【分析】求出与105°,60°的内角相邻的外角的度数,根据多边形的外角和是360°,即可求解.
【解答】解:∠1=180﹣∠BAD=180﹣105=75°,
∠2=180﹣∠ABC=180﹣60=120°.
根据多边形外角和定理可得:∠1+∠2+2x+x=360,
即:75+120+2x+x=360,
解得:x=55°.
19.如图,在Rt△ABC中,∠C=90°,D为AB的中点,E为AC的中点,∠A=30°,AB=12,则DE的长度是 3 .
【分析】先根据直角三角形的性质求出BC的长,再由三角形中位线定理即可得出结论.
【解答】解:∵在Rt△ABC中,∠C=90°,∠A=30°,AB=12,
∴BC=AB=6.
∵D为AB的中点,E为AC的中点,
∴DE是△ABC的中位线,
∴DE=BC=3.
故答案为:3.
20.一个多边形的内角和比其外角和的2倍多180°,则该多边形的对角线的条数是 14 .
【分析】多边形的内角和比外角和的2倍多180°,而多边形的外角和是360°,则内角和是900度,n边形的内角和可以表示成(n﹣2)?180°,设这个多边形的边数是n,就得到方程,从而求出边数,进而求出对角线的条数.
【解答】解:根据题意,得
(n﹣2)?180=360°×2+180°,
解得:n=7.
则这个多边形的边数是7,
七边形的对角线条数为=14,
故答案为:14.
三、解答题(共5小题,满分40分)
21.(6分)已知:如图,E,F是?ABCD的对角线AC上两点,AF=CE,求证:DF=BE,DF∥BE.
【分析】可由题中条件求解△ABE≌△CDF,得出DF=BE,∠AEB=∠CFD,即∠BEC=∠DFA,进而可求证DF与BE平行.
【解答】证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
又∵AE=CF,
∴△ABE≌△CDF(SAS),
∴DF=BE,∠AEB=∠CFD,
∴∠BEC=∠DFA,
∴DF∥BE.
22.(8分)已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC
边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
【分析】(1)利用有两条边对应相等并且夹角相等的两个三角形全等即可证明△AFB≌△ADC;
(2)四边形BCEF是平行四边形,因为△AFB≌△ADC,所以可得∠ABF=∠C=60°,进而证明∠ABF=∠BAC,则可得到FB∥AC,又BC∥EF,所以四边形BCEF是平行四边形;
(3)易证AF=AD,AB=AC,∠FAD=∠BAC=60°,可得∠FAB=∠DAC,即可证明△AFB≌△ADC;根据△AFB≌△ADC可得∠ABF=∠ADC,进而求得∠AFB=∠EAF,求得BF∥AE,又BC∥EF,从而证得四边形BCEF是平行四边形.
【解答】证明:(1)∵△ABC和△ADF都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠FAD﹣∠BAD,∠DAC=∠BAC﹣∠BAD,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
,
∴△AFB≌△ADC(SAS);
(2)由①得△AFB≌△ADC,
∴∠ABF=∠C=60°.
又∵∠BAC=∠C=60°,
∴∠ABF=∠BAC,
∴FB∥AC,
又∵BC∥EF,
∴四边形BCEF是平行四边形;
(3)成立,理由如下:
∵△ABC和△ADF都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠BAC﹣∠FAE,∠DAC=∠FAD﹣∠FAE,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
,
∴△AFB≌△ADC(SAS);
∴∠AFB=∠ADC.
又∵∠ADC+∠DAC=60°,∠EAF+∠DAC=60°,
∴∠ADC=∠EAF,
∴∠AFB=∠EAF,
∴BF∥AE,
又∵BC∥EF,
∴四边形BCEF是平行四边形.
23.(8分)如图,△ABC中,BC>AC,点D在BC上,且CA=CD,∠ACB的平分线交AD于点F,E是AB的中点.
(1)求证:EF∥BD;
(2)若∠ACB=60°,AC=8,BC=12,求四边形BDFE的面积.
【分析】(1)根据等腰三角形三线合一的性质可得CF是AD边的中线,然后求出EF是△ABD的中位线,再根据三角形的中位线平行于第三边证明;
(2)判断出△CAD是等边三角形,然后求出BD,过点A作AM⊥BC,垂足为M,根据等边三角形的性质求出AM,从而求出△ABD的面积,然后求出根据△AEF和△ABD相似,求出△AEF的面积,再求解即可.
【解答】(1)证明:∵CA=CD,CF平分∠ACB,
∴CF是AD边的中线,
∵E是AB的中点,
∴EF是△ABD的中位线.
∴EF∥BD;
(2)解:∵∠ACB=60°,CA=CD,
∴△CAD是等边三角形,
∴∠ADC=60°,AD=DC=AC=8,
∴BD=BC﹣CD=12﹣8=4,
过点A作AM⊥BC,垂足为M,
∴AM=AD=×8=4,
S△ABD=BD?AM=×4×4=8,
∵EF∥BD,
∴△AEF∽△ABD,且=,
∴=,
∴S△AEF=×8=2,
四边形BDFE的面积=S△ABD﹣S△AEF=8﹣2=6.
24.(9分)如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
【分析】(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC,DG∥BC且DG=BC,从而得到DE=EF,DG∥EF,再利用一组对边平行且相等的四边形是平行四边形证明即可;
(2)先判断出∠BOC=90°,再利用直角三角形斜边的中线等于斜边的一半,求出EF即可.
【解答】解:(1)∵D、G分别是AB、AC的中点,
∴DG∥BC,DG=BC,
∵E、F分别是OB、OC的中点,
∴EF∥BC,EF=BC,
∴DG=EF,DG∥EF,
∴四边形DEFG是平行四边形;
(2)∵∠OBC和∠OCB互余,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°,
∵M为EF的中点,OM=3,
∴EF=2OM=6.
由(1)有四边形DEFG是平行四边形,
∴DG=EF=6.
25.(9分)如图所示,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P从A向点D以1cm/s的速度运动,到点D即停止.点Q从点C向点B以2cm/s的速度运动,到点B即停止.直线PQ将四边形ABCD截得两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形?
【分析】①若四边形ABQP是平行四边形,则AP=BQ,进而求出t的值;②若四边形PQCD是平行四边形,则PD=CQ,进而求出t的值.
【解答】解:设当P,Q两点同时出发,t秒后,四边形ABQP或四边形PQCD是平行四边形,
根据题意可得:
AP=tcm,PD=(24﹣t)cm,CQ=2tcm,BQ=(30﹣2t)cm,
①若四边形ABQP是平行四边形,
则AP=BQ,
∴t=30﹣2t,
解得:t=10,
∴10s后四边形ABQP是平行四边形;
②若四边形PQCD是平行四边形,
则PD=CQ,
∴24﹣t=2t,
解得:t=8,
∴8s后四边形PQCD是平行四边形;
综上所述:当P,Q两点同时出发,8秒或10秒后,四边形ABQP或四边形PQCD是平行四边形.
平行四边形
一、选择题(共12小题,每小题3分,共36分)
1.已知四边形ABCD,有以下四个条件:
(1)AB=AD,AB=BC;(2)∠A=∠B,∠C=∠D;(3)AB∥CD,AB=CD;(4)AB∥CD,AD∥BC.
其中能判定四边形ABCD是平行四边形的有( )个.
A.1
B.2
C.3
D.4
2.平行四边形一边的长是10cm,那么这个平行四边形的两条对角线长可以是( )
A.4cm,6cm
B.6cm,8cm
C.8cm,12cm
D.20cm,30cm
3.如图所示,?ABCD的对角线AC,BD相交于点O,AE=EB,OE=3,AB=5,?ABCD的周长( )
A.11
B.13
C.16
D.22
4.如图,?ABCD的对角线AC,BD交于点O,AC⊥AB,AB=,且AC:BD=2:3,那么AC的长为( )
A.2
B.
C.3
D.4
5.如图,在?ABCD中,AB=3,AD=5,∠BCD的平分线交BA的延长线于点E,则AE的长为( )
A.3
B.2.5
C.2
D.1.5
6.如果一个正多边形内角和等于1080°,那么这个正多边形的每一个外角等于( )
A.45°
B.60°
C.120°
D.135°
7.如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=,AC=2,BD=4,则AE的长为( )
A.
B.
C.
D.
8.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
A.∠A=∠1+∠2
B.3∠A=2∠1+∠2
C.2∠A=∠1+∠2
D.3∠A=2(∠1+∠2)
9.如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点O,点F、G分别是OB、OC的中点,连接AO.若AO=3cm,BC=4cm,则四边形DEFG的周长是( )
A.7cm
B.9cm
C.12cm
D.14cm
10.如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD的中点∠ABD=20°,∠BDC=70°,则∠NMP的度数为( )
A.50°
B.25°
C.15°
D.20°
11.把一个多边形割去一个角后,得到的多边形内角和为1440°,请问这个多边形原来的边数为( )
A.9
B.10
C.11
D.以上都有可能
12.如图,△ABC的面积是12,点D、E、F、G分别是BC、AD、BE、CE的中点,则△AFG的面积是( )
A.4.5
B.5
C.5.5
D.6
二、填空题(共8小题,每小题3分,共24分)
13.如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为
.
14.如图,在?ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是
.
15.已知:在?ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AD于E、BC于F,S△AOE=3,S△BOF=5,则?ABCD的面积是
.
16.把正三角形、正四边形、正五边形按如图所示的位置摆放,若∠1=52°,∠2=18°,则∠3=
.
17.如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=
厘米.
18.如图所示,x的值为
.
19.如图,在Rt△ABC中,∠C=90°,D为AB的中点,E为AC的中点,∠A=30°,AB=12,则DE的长度是
.
20.一个多边形的内角和比其外角和的2倍多180°,则该多边形的对角线的条数是
.
三、解答题(共5小题,满分40分)
21.(6分)已知:如图,E,F是?ABCD的对角线AC上两点,AF=CE,求证:DF=BE,DF∥BE.
22.(8分)已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC
边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
23.(8分)如图,△ABC中,BC>AC,点D在BC上,且CA=CD,∠ACB的平分线交AD于点F,E是AB的中点.
(1)求证:EF∥BD;
(2)若∠ACB=60°,AC=8,BC=12,求四边形BDFE的面积.
24.(9分)如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
25.(9分)如图所示,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P从A向点D以1cm/s的速度运动,到点D即停止.点Q从点C向点B以2cm/s的速度运动,到点B即停止.直线PQ将四边形ABCD截得两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形?
参考答案与试题解析
一、选择题(共12小题,每小题3分,共36分)
1.已知四边形ABCD,有以下四个条件:
(1)AB=AD,AB=BC;(2)∠A=∠B,∠C=∠D;(3)AB∥CD,AB=CD;(4)AB∥CD,AD∥BC.
其中能判定四边形ABCD是平行四边形的有( )个.
A.1
B.2
C.3
D.4
【分析】平行四边形的判定:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形.
【解答】解:根据平行四边形的判定定理知,(1),(2)不符合是平行四边形的条件;
(3)(4)满足四边形是平行四边形.
故选:B.
2.平行四边形一边的长是10cm,那么这个平行四边形的两条对角线长可以是( )
A.4cm,6cm
B.6cm,8cm
C.8cm,12cm
D.20cm,30cm
【分析】平行四边形的这条边和两条对角线的一半构成三角形,应该满足第三边大于两边之差小于两边之和才能构成三角形.
【解答】解:A、∵2+3<10,不能够成三角形,故此选项错误;
B、4+3<10,不能够成三角形,故此选项错误;
C、4+6=10,不能构成三角形,故此选项错误;
D、10+10>15,能够成三角形,故此选项正确;
故选:D.
3.如图所示,?ABCD的对角线AC,BD相交于点O,AE=EB,OE=3,AB=5,?ABCD的周长( )
A.11
B.13
C.16
D.22
【分析】由?ABCD的对角线AC,BD相交于点O,AE=EB,易得DE是△ABC的中位线,即可求得BC的长,继而求得答案.
【解答】解:∵?ABCD的对角线AC,BD相交于点O,
∴OA=OC,AD=BC,AB=CD=5,
∵AE=EB,OE=3,
∴BC=2OE=6,
∴?ABCD的周长=2×(AB+BC)=22.
故选:D.
4.如图,?ABCD的对角线AC,BD交于点O,AC⊥AB,AB=,且AC:BD=2:3,那么AC的长为( )
A.2
B.
C.3
D.4
【分析】根据平行四边形的性质可知,OA=OC,OB=OD,由AC:BD=2:3,推出OA:OB=2:3,设OA=2m,OB=3m,在Rt△AOB中利用勾股定理即可解决问题.
【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AC:BD=2:3,
∴OA:OB=2:3,设OA=2m,BO=3m,
∵AC⊥BD,
∴∠BAO=90°,
∴OB2=AB2+OA2,
∴9m2=5+4m2,
∴m=±1,
∵m>0,
∴m=1,
∴AC=2OA=4.
故选:D.
5.如图,在?ABCD中,AB=3,AD=5,∠BCD的平分线交BA的延长线于点E,则AE的长为( )
A.3
B.2.5
C.2
D.1.5
【分析】由平行四边形ABCD中,CE平分∠BCD,可证得△BCE是等腰三角形,继而利用AE=BE﹣AB,求得答案.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=5,
∴∠E=∠ECD,
∵CE平分∠BCD,
∴∠BCE=∠ECD,
∴∠E=∠BCE,
∴BE=BC=5,
∴AE=BE﹣AB=5﹣3=2;故选:C.
6.如果一个正多边形内角和等于1080°,那么这个正多边形的每一个外角等于( )
A.45°
B.60°
C.120°
D.135°
【分析】首先设此多边形为n边形,根据题意得:180(n﹣2)=1080,即可求得n=8,再由多边形的外角和等于360°,即可求得答案.
【解答】解:设此多边形为n边形,
根据题意得:180(n﹣2)=1080,
解得:n=8,
∴这个正多边形的每一个外角等于:360°÷8=45°.
故选:A.
7.如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=,AC=2,BD=4,则AE的长为( )
A.
B.
C.
D.
【分析】由勾股定理的逆定理可判定△BAO是直角三角形,所以平行四边形ABCD的面积即可求出.
【解答】解:∵AC=2,BD=4,四边形ABCD是平行四边形,
∴AO=AC=1,BO=BD=2,
∵AB=,
∴AB2+AO2=BO2,
∴∠BAC=90°,
∵在Rt△BAC中,BC===
S△BAC=×AB×AC=×BC×AE,
∴×2=AE,
∴AE=,
故选:D.
8.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
A.∠A=∠1+∠2
B.3∠A=2∠1+∠2
C.2∠A=∠1+∠2
D.3∠A=2(∠1+∠2)
【分析】根据三角形的内角和定理,以及四边形的内角和定理即可求出答案.
【解答】解:由题意可知:∠AED+∠ADE=180°﹣∠A,
∠B+∠C=180°﹣∠A
∵∠AED+∠ADE+∠1+∠2+∠B+∠C=360°,
∴360°﹣2∠A+∠1+∠2=360°,
∴2∠A=∠1+∠2,
故选:C.
9.如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点O,点F、G分别是OB、OC的中点,连接AO.若AO=3cm,BC=4cm,则四边形DEFG的周长是( )
A.7cm
B.9cm
C.12cm
D.14cm
【分析】根据三角形中位线定理分别求出DE、EF、FG、DG,计算即可.
【解答】解:∵BD、CE是△ABC的中线,
∴DE=BC=2,
同理,FG=BC=2,EF=OA=1.5,DG=OA=1.5,
∴四边形DEFG的周长=DE+EF+FG+DG=7(cm),
故选:A.
10.如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD的中点∠ABD=20°,∠BDC=70°,则∠NMP的度数为( )
A.50°
B.25°
C.15°
D.20°
【分析】根据中位线定理和已知,易证明△PMN是等腰三角形,根据等腰三角形的性质和已知条件即可求出∠PMN的度数.
【解答】解:∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线,
∴PM=AB,PN=DC,PM∥AB,PN∥DC,
∵AB=CD,
∴PM=PN,
∴△PMN是等腰三角形,
∵PM∥AB,PN∥DC,
∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°,
∴∠MPN=∠MPD+∠NPD=20°+(180﹣70)°=130°,
∴∠PMN==25°.
故选:B.
11.把一个多边形割去一个角后,得到的多边形内角和为1440°,请问这个多边形原来的边数为( )
A.9
B.10
C.11
D.以上都有可能
【分析】先根据多边形的内角和公式(n﹣2)?180°求出截去一个角后的多边形的边数,再根据截去一个角后边数增加1,不变,减少1讨论得解.
【解答】解:设多边形截去一个角的边数为n,
则(n﹣2)?180°=1440°,
解得n=10,
∵截去一个角后边上可以增加1,不变,减少1,
∴原多边形的边数是9或10或11.
故选:D.
12.如图,△ABC的面积是12,点D、E、F、G分别是BC、AD、BE、CE的中点,则△AFG的面积是( )
A.4.5
B.5
C.5.5
D.6
【分析】根据中线的性质,可得△AEF的面积=×△ABE的面积=×△ABD的面积=×△ABC的面积=,△AEG的面积=,根据三角形中位线的性质可得△EFG的面积=×△BCE的面积=,进而得到△AFG的面积.
【解答】解:∵点D,E,F,G分别是BC,AD,BE,CE的中点,
∴AD是△ABC的中线,BE是△ABD的中线,CE是△ACD的中线,AF是△ABE的中线,AG是△ACE的中线,
∴△AEF的面积=×△ABE的面积=×△ABD的面积=×△ABC的面积=,
同理可得△AEG的面积=,
△BCE的面积=×△ABC的面积=6,
又∵FG是△BCE的中位线,
∴△EFG的面积=×△BCE的面积=,
∴△AFG的面积是×3=,
故选:A.
二、填空题(共8小题,每小题3分,共24分)
13.如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 36° .
【分析】由平行四边形的性质得出∠D=∠B=52°,由折叠的性质得:∠D′=∠D=52°,∠EAD′=∠DAE=20°,由三角形的外角性质求出∠AEF=72°,与三角形内角和定理求出∠AED′=108°,即可得出∠FED′的大小.
【解答】解:∵四边形ABCD是平行四边形,
∴∠D=∠B=52°,
由折叠的性质得:∠D′=∠D=52°,∠EAD′=∠DAE=20°,
∴∠AEF=∠D+∠DAE=52°+20°=72°,∠AED′=180°﹣∠EAD′﹣∠D′=108°,
∴∠FED′=108°﹣72°=36°;
故答案为:36°.
14.如图,在?ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是 24 .
【分析】根据平行四边形性质得出AD∥CB,AB∥CD,推出∠DAB+∠CBA=180°,求出∠PAB+∠PBA=90°,在△APB中求出∠APB=90°,由勾股定理求出BP,证出AD=DP=5,BC=PC=5,得出DC=10=AB,即可求出答案.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°﹣(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=5,
同理:PC=CB=5,
即AB=DC=DP+PC=10,
在Rt△APB中,AB=10,AP=8,
∴BP==6,
∴△APB的周长=6+8+10=24;
故答案为:24.
15.已知:在?ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AD于E、BC于F,S△AOE=3,S△BOF=5,则?ABCD的面积是 32 .
【分析】利用平行四边形的性质可证明△AOE≌△COF,所以可得△COF的面积为3,进而可得△BOC的面积为8,又因为△BOC的面积=?ABCD的面积,进而可得问题答案.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠FCO=∠EAC,
又∵AO=CO,∠AOE=∠COF,
∴△AOE≌△COF
∴△COF的面积为3,
∵S△BOF=5,
∴△BOC的面积为8,
∵△BOC的面积=?ABCD的面积,
∴?ABCD的面积=4×8=32,
故答案为:32.
16.把正三角形、正四边形、正五边形按如图所示的位置摆放,若∠1=52°,∠2=18°,则∠3= 32° .
【分析】利用360°减去等边三角形的一个内角的度数,减去正方形的一个内角的度数,减去正五边形的一个内角的度数,然后减去∠1和∠2即可求得.
【解答】解:等边三角形的内角的度数是60°,正方形的内角度数是90°,正五边形的内角的度数是:(5﹣2)×180°=108°,
则∠3=360°﹣60°﹣90°﹣108°﹣∠1﹣∠2=32°.
故答案是:32°.
17.如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF= 3 厘米.
【分析】根据AC+BD=24厘米,可得出出OA+OB=12cm,继而求出AB,判断EF是△OAB的中位线即可得出EF的长度.
【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵AC+BD=24厘米,
∴OA+OB=12cm,
∵△OAB的周长是18厘米,
∴AB=6cm,
∵点E,F分别是线段AO,BO的中点,
∴EF是△OAB的中位线,
∴EF=AB=3cm.
故答案为:3.
18.如图所示,x的值为 55° .
【分析】求出与105°,60°的内角相邻的外角的度数,根据多边形的外角和是360°,即可求解.
【解答】解:∠1=180﹣∠BAD=180﹣105=75°,
∠2=180﹣∠ABC=180﹣60=120°.
根据多边形外角和定理可得:∠1+∠2+2x+x=360,
即:75+120+2x+x=360,
解得:x=55°.
19.如图,在Rt△ABC中,∠C=90°,D为AB的中点,E为AC的中点,∠A=30°,AB=12,则DE的长度是 3 .
【分析】先根据直角三角形的性质求出BC的长,再由三角形中位线定理即可得出结论.
【解答】解:∵在Rt△ABC中,∠C=90°,∠A=30°,AB=12,
∴BC=AB=6.
∵D为AB的中点,E为AC的中点,
∴DE是△ABC的中位线,
∴DE=BC=3.
故答案为:3.
20.一个多边形的内角和比其外角和的2倍多180°,则该多边形的对角线的条数是 14 .
【分析】多边形的内角和比外角和的2倍多180°,而多边形的外角和是360°,则内角和是900度,n边形的内角和可以表示成(n﹣2)?180°,设这个多边形的边数是n,就得到方程,从而求出边数,进而求出对角线的条数.
【解答】解:根据题意,得
(n﹣2)?180=360°×2+180°,
解得:n=7.
则这个多边形的边数是7,
七边形的对角线条数为=14,
故答案为:14.
三、解答题(共5小题,满分40分)
21.(6分)已知:如图,E,F是?ABCD的对角线AC上两点,AF=CE,求证:DF=BE,DF∥BE.
【分析】可由题中条件求解△ABE≌△CDF,得出DF=BE,∠AEB=∠CFD,即∠BEC=∠DFA,进而可求证DF与BE平行.
【解答】证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
又∵AE=CF,
∴△ABE≌△CDF(SAS),
∴DF=BE,∠AEB=∠CFD,
∴∠BEC=∠DFA,
∴DF∥BE.
22.(8分)已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC
边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
【分析】(1)利用有两条边对应相等并且夹角相等的两个三角形全等即可证明△AFB≌△ADC;
(2)四边形BCEF是平行四边形,因为△AFB≌△ADC,所以可得∠ABF=∠C=60°,进而证明∠ABF=∠BAC,则可得到FB∥AC,又BC∥EF,所以四边形BCEF是平行四边形;
(3)易证AF=AD,AB=AC,∠FAD=∠BAC=60°,可得∠FAB=∠DAC,即可证明△AFB≌△ADC;根据△AFB≌△ADC可得∠ABF=∠ADC,进而求得∠AFB=∠EAF,求得BF∥AE,又BC∥EF,从而证得四边形BCEF是平行四边形.
【解答】证明:(1)∵△ABC和△ADF都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠FAD﹣∠BAD,∠DAC=∠BAC﹣∠BAD,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
,
∴△AFB≌△ADC(SAS);
(2)由①得△AFB≌△ADC,
∴∠ABF=∠C=60°.
又∵∠BAC=∠C=60°,
∴∠ABF=∠BAC,
∴FB∥AC,
又∵BC∥EF,
∴四边形BCEF是平行四边形;
(3)成立,理由如下:
∵△ABC和△ADF都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠BAC﹣∠FAE,∠DAC=∠FAD﹣∠FAE,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
,
∴△AFB≌△ADC(SAS);
∴∠AFB=∠ADC.
又∵∠ADC+∠DAC=60°,∠EAF+∠DAC=60°,
∴∠ADC=∠EAF,
∴∠AFB=∠EAF,
∴BF∥AE,
又∵BC∥EF,
∴四边形BCEF是平行四边形.
23.(8分)如图,△ABC中,BC>AC,点D在BC上,且CA=CD,∠ACB的平分线交AD于点F,E是AB的中点.
(1)求证:EF∥BD;
(2)若∠ACB=60°,AC=8,BC=12,求四边形BDFE的面积.
【分析】(1)根据等腰三角形三线合一的性质可得CF是AD边的中线,然后求出EF是△ABD的中位线,再根据三角形的中位线平行于第三边证明;
(2)判断出△CAD是等边三角形,然后求出BD,过点A作AM⊥BC,垂足为M,根据等边三角形的性质求出AM,从而求出△ABD的面积,然后求出根据△AEF和△ABD相似,求出△AEF的面积,再求解即可.
【解答】(1)证明:∵CA=CD,CF平分∠ACB,
∴CF是AD边的中线,
∵E是AB的中点,
∴EF是△ABD的中位线.
∴EF∥BD;
(2)解:∵∠ACB=60°,CA=CD,
∴△CAD是等边三角形,
∴∠ADC=60°,AD=DC=AC=8,
∴BD=BC﹣CD=12﹣8=4,
过点A作AM⊥BC,垂足为M,
∴AM=AD=×8=4,
S△ABD=BD?AM=×4×4=8,
∵EF∥BD,
∴△AEF∽△ABD,且=,
∴=,
∴S△AEF=×8=2,
四边形BDFE的面积=S△ABD﹣S△AEF=8﹣2=6.
24.(9分)如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
【分析】(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC,DG∥BC且DG=BC,从而得到DE=EF,DG∥EF,再利用一组对边平行且相等的四边形是平行四边形证明即可;
(2)先判断出∠BOC=90°,再利用直角三角形斜边的中线等于斜边的一半,求出EF即可.
【解答】解:(1)∵D、G分别是AB、AC的中点,
∴DG∥BC,DG=BC,
∵E、F分别是OB、OC的中点,
∴EF∥BC,EF=BC,
∴DG=EF,DG∥EF,
∴四边形DEFG是平行四边形;
(2)∵∠OBC和∠OCB互余,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°,
∵M为EF的中点,OM=3,
∴EF=2OM=6.
由(1)有四边形DEFG是平行四边形,
∴DG=EF=6.
25.(9分)如图所示,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P从A向点D以1cm/s的速度运动,到点D即停止.点Q从点C向点B以2cm/s的速度运动,到点B即停止.直线PQ将四边形ABCD截得两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形?
【分析】①若四边形ABQP是平行四边形,则AP=BQ,进而求出t的值;②若四边形PQCD是平行四边形,则PD=CQ,进而求出t的值.
【解答】解:设当P,Q两点同时出发,t秒后,四边形ABQP或四边形PQCD是平行四边形,
根据题意可得:
AP=tcm,PD=(24﹣t)cm,CQ=2tcm,BQ=(30﹣2t)cm,
①若四边形ABQP是平行四边形,
则AP=BQ,
∴t=30﹣2t,
解得:t=10,
∴10s后四边形ABQP是平行四边形;
②若四边形PQCD是平行四边形,
则PD=CQ,
∴24﹣t=2t,
解得:t=8,
∴8s后四边形PQCD是平行四边形;
综上所述:当P,Q两点同时出发,8秒或10秒后,四边形ABQP或四边形PQCD是平行四边形.
