苏科版九年级数学下册相似三角形题型归纳(含隐圆、动点、最值、拓展、压轴)(无答案)
文档属性
| 名称 | 苏科版九年级数学下册相似三角形题型归纳(含隐圆、动点、最值、拓展、压轴)(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 880.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-15 22:12:45 | ||
图片预览



文档简介
相似三角形(相似动点)分类
涉及隐圆问题、最值问题、分类讨论题型、动点题型、压轴题、拓展题
题型分类:
一、相似三角形的判定定理
①平行于三角形一边的直线和其他两边或其延长线相交,所得的三角形与原三角形相似;
②三边对应成比例的两个三角形相似;
③两角对应相等的两个三角形相似;
两边对应成比例且夹角相等的两个三角形相似。
二、相似三角形解题思路:
(1)相似三角形有公共角或对顶角时,公共角或对顶角是最明显的对应角;相似三角形中最大的角(或最小的角)一定是对应角;相似三角形中,一对相等的角是对应角,对应角所对的边是对应边,对应角的夹边是对应边;
(2)相似三角形中,一对最长的边(或最短的边)一定是对应边;对应边所对的角是对应角;对应边所夹的角是对应角.
2、常见的相似三角形的基本图形:
三角形相似的判定,要与三角形全等的判定相比较,把证明三角形全等的思想方法迁移到相似三角形中来;对一些出现频率较高的图形,要善于归纳和记忆;对相似三角形的判定思路要善于总结,形成一整套完整的判定方法.如:
(1)“平行线型”相似三角形。
(2)“相交线型”相似三角形。
(3)“旋转型”相似三角形。
三、相似模型
1.A字、8字模型。
2.共边共角模型(扭屁股模型)。
3.一线三等角模型。
4.倒数模型(较难)
5.圆中的相似。
6.平行线分线段成比例。
类型一、线段比例问题
1.
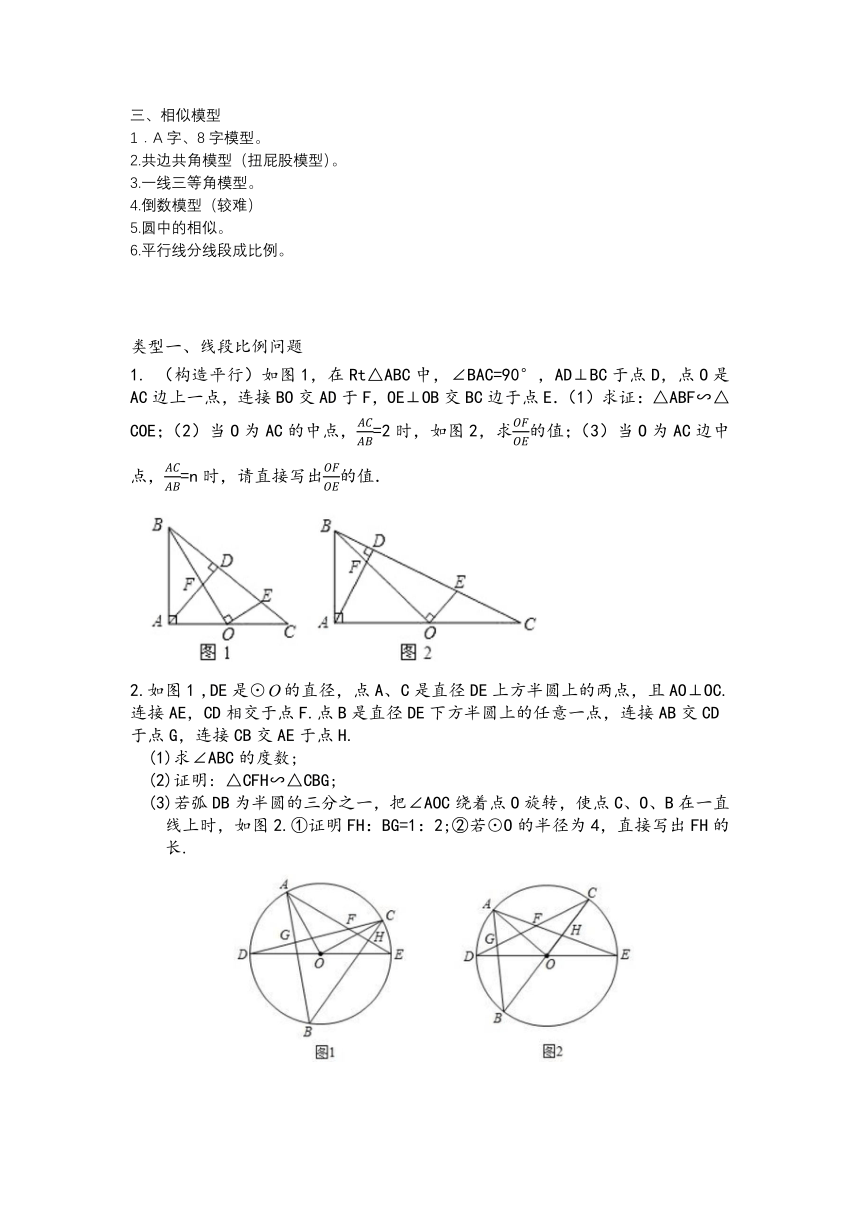
(构造平行)如图1,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO交AD于F,OE⊥OB交BC边于点E.(1)求证:△ABF∽△COE;(2)当O为AC的中点,=2时,如图2,求的值;(3)当O为AC边中点,=n时,请直接写出的值.
2.如图1
,DE是⊙的直径,点A、C是直径DE上方半圆上的两点,且AO⊥OC.连接AE,CD相交于点F.点B是直径DE下方半圆上的任意一点,连接AB交CD
于点G,连接CB交AE于点H.
(1)求∠ABC的度数;
(2)证明:
△CFH∽△CBG;
(3)若弧DB为半圆的三分之一,把∠AOC绕着点O旋转,使点C、O、B在一直线上时,如图2.①证明FH:BG=1:2;②若⊙O的半径为4,直接写出FH的长.
3.
已知抛物线(a≠0),与x轴从左至右依次相交于A、B两点,与y轴相交于点C,经过点A的直线y=-x+b与抛物线的另一个交点为D.
(1)若点D的横坐标为2,求抛物线的函数解析式;
(2)若在第三象限内的抛物线上有点P,使得以A、B、P为顶点的三角形与△ABC相似,求点P的坐标;
(3)在(1)的条件下,设点E是线段AD上的一点(不含端点),连接BE.一动点Q从点B出发,沿线段BE以每秒1个单位的速度运动到点E,再沿线段ED以每秒
个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?
二、相似比乘积处理方法(逆向和正向分析找解题思路)
1.如果四边形ABCD的对角线交于O,过O作直线OG∥AB交BC于E,交AD于F,交CD的延长线于G,求证:OG2=GE·GF.
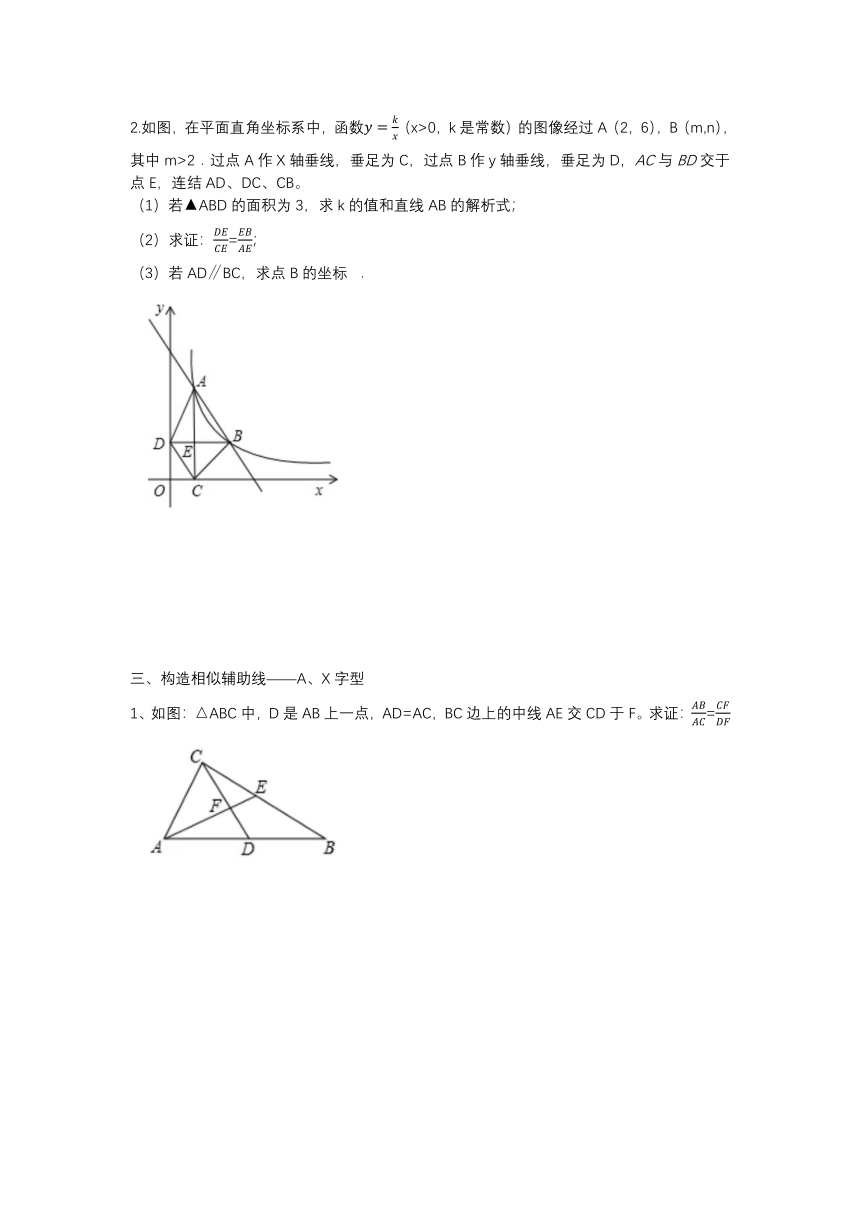
2.如图,在平面直角坐标系中,函数(x>0,k是常数)的图像经过A(2,6),B(m,n),其中m>2.过点A作X轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连结AD、DC、CB。
(1)若▲ABD的面积为3,求k的值和直线AB的解析式;
(2)求证:=;
(3)若AD∥BC,求点B的坐标
.
三、构造相似辅助线——A、X字型
1、如图:△ABC中,D是AB上一点,AD=AC,BC边上的中线AE交CD于F。求证:=
2.如图,在Rt▲ACB中,∠ACB=90°,AC=2
cm,AB=4
cm,动点P从点C出发,在BC边上以每秒cm的速度向点B匀速运动,同时动点Q也从点C出发,沿C-A-B以每秒4cm的速度匀速运动,运动时间为t秒(0(1)当t=时,求▲PCQ的面积;
(2)设⊙O的面积为s,求s与t的函数关系式;
(3)当点Q在AB上运动时,⊙O与Rt▲ABC的一边相切,求t的值.
3.如图,在等腰直角三角形ABC中,∠BAC=90°,AC=8cm,AD⊥BC于点D,点P从点A出发,沿A→C方向以cm/s的速度运动到点C停止,在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
(1)当点M落在AB上时,x= ;
(2)当点M落在AD上时,x= ;
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
相似类定值问题以及存在性问题
1.如图,四边形ABCD是矩形,点P是对角线AC上一动点(不与A、C重合),连接PB,过点作PE⊥PB,交射线DC于点E,已知AD=3,sin∠BAC=.设AP的长为x.
(1)AB=
;当x=1时,
;
(2)①试探究:否是定值?若是,请求出这个值;若不是,请说明理由;
②连接BE,设▲PBE的面积为S,求S的最小值.
(3)当▲PCE是等腰三角形时.请求出x的值;
(2018年苏州园区一模)
2.如图,正方形ABCD与矩形EFGH在直线l的同侧,边AD、EH在直线l上.保持正方形ABCD不动,并将矩形EFGH以1
cm/s的速度沿DA方向移动,移动开始前点E与点D重合,当矩形EFGH完全穿过正方形ABCD
(即点H与A点重合)时停止移动,设移动时间为t
(s).已知AD=cm,EH=
cm,EF=
cm,连接AF、CG.
(1)矩形EFGH从开始移动到完全穿过正方形ABCD,所用时间为
s;
(2)当AF⊥CG时,求t的值;
3.已知,如图1,直线y=x+3与x轴、y轴分别交于A、C两点,点B在x轴上,点B的横坐标为,抛物线经过A、B、C三点.点D直线AC上方抛物线上任意一点.
(1)求抛物线的函数关系式;
(2)若P为线段AC上一点,且S▲PCD=2S▲PAD,求点P的坐标;
五、证明线段相等
1.在面积为24的△ABC中,矩形DEFG的边DE在AB上运动,点F、G分别在BC、AC上。
(1)若AE=8,DE=2EF,求GF的长;(2)若∠ACB=90°,如图2,线段DM、EN分别为△ADG和△BEF的角平分线,求证:MG=NF;(3)请直接写出矩形DEFG的面积的最大值。
2、在△ABC中,点D从A出发,在AB边上以每秒一个单位的速度向B运动,同时点F从B出发,在BC边上以相同的速度向C运动,过点D作DE∥BC交AC于点E.运动时间为t秒.
(1)若AB=5,BC=6,当t为何值时,四边形DFCE为平行四边形;(2)连接AF、CD.若BD=DE,求证:∠BAF=∠BCD;(3)AF交DE于点M,在DC上取点N,使MN∥AC,连接FN.
①求证:=;②若AB=5,BC=6,AC=4,当MN=FN时,请直接写出t的值.
3.如图,Rt▲ABC中,∠A=90°,以AB为直径的⊙O交BC边交于点E,
EF⊥AB,垂足为F.D为AC的中点,连结BD交EF于G.
(1)求证:ED是⊙O的切线;
(2)求证:EG=FG;
(3)若DG=DA=4,求O的半径.
最值问题
1.如图,在Rt▲ABC中,∠A=30°,AC=8,以C为圆心,4为半径作⊙C.
(1)试判断⊙C与AB的位置关系,并说明理由;
(2)点F是⊙C上一动点,点D在AC上且CD=2,试说明▲FCD
:▲ACF;
(3)点E是AB边上任意一点,在(2)的情况下,试求出EF+FA的最小值.
2.如图,抛物线y=a2-3ax+c(a≠0)与x轴交于A,B两点,交y轴于点C,其中A(-1,0),C(0,3).
求抛物线的解析式
点P是线段BC上方抛物线上一动点(不与B,C重合),过点P作PD⊥x轴,垂足为D,交BC于点E,作PF⊥直线BC于点F,设点P的横坐标为x,△PEF的周长记为l,求l关于x的函数关系式,并求出l的最大值及此时点P的坐标
点H是直线AC上一点,该抛物线的对称轴上一动点G,连接OG,GH,则两线段OG,GH的长度之和的最小值等于______,此时点G的坐标为_____(直接写出答案。)
3.如图,Rt△ABC中.∠BAC=90°,AB=1,AC=2.点D,E分别是边BC.AC上的动点,
则DA+DE的最小值为
七、
相似基本模型应用
1.如图,四边形ABCD的对角线交于点O,且AB∥CD有以下四个结论:
①▲AOB:▲COD
②▲AOD:▲ACB
③S▲DOC:S▲AOD=DC:AB
④S▲AOD=S▲BOC
其中,始终正确的有(
)
A.
1个
B.
2个
C.
3个
D.
4个
2.如图,己知Rt▲ABC的直角边AC与Rt▲DEF的直角边DF在同一条直线上,且AC=60cm,
BC=45cm,
DE=6cm,
EF=8cm.现将点C与点F重合,再以4
cm/s的速度沿CA方向移动▲DEF;同时,点P从点A出发,以5
cm/s的速度沿AB方向移动,设移动时间为t
(s).以点P为圆心,3t
(cm)长为半径的⊙P与AB相交于点M、N.当点F与点A重合时,▲DEF与点P同时停止移动.在移动的过程中,
(1)连接ME,当ME∥AC时,t=
s;
(2)连接NF,当NF平分DE时,求t的值;
3.在Rt▲ABC中,∠C=90°,Rt▲ABC绕点A顺时针旋转到Rt▲ADE的
位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.
如图1,若点F与点A重合,求证:AC=BC;
(2)若∠DAF=∠DBA,
①如图2,当点F在线段CA的延长线上时,判断线段AF与线段BE的数量关系,并说明理由;
(母子相似)②当点F在线段CA上时,设BE=x,请用含x的代数式表示线段AF.
八、与圆有关的相似
1.(隐圆相似)如图,在Rt▲ABC中,∠ACB=90°,BC=6,AC=8.点D、E分别是边AB、BC的中点,连接DE,将▲BDE绕点B按顺时针方向旋转一定角度(这个角度小于90?)后,点D的对应点D“和点E的对应点E”以及点A三个点在一直线上,连接CE“,则CE“=
.
2.(最值问题)如图,AB是半⊙O的直径,且AB=8.点C是半⊙O上的一个动点(不与点A、B重合),过点C作CD⊥AB,垂足为D.设AC=x,AD=y,则x-y的最大值等于
.
3.(最值问题)如图,在▲ABC中,∠ACB=90°,BC=12,AC=9,以点C为圆心,6为半径的圆上有一个动点D.连接AD、BD、CD,则AD+BD的最小值是
.
涉及隐圆问题、最值问题、分类讨论题型、动点题型、压轴题、拓展题
题型分类:
一、相似三角形的判定定理
①平行于三角形一边的直线和其他两边或其延长线相交,所得的三角形与原三角形相似;
②三边对应成比例的两个三角形相似;
③两角对应相等的两个三角形相似;
两边对应成比例且夹角相等的两个三角形相似。
二、相似三角形解题思路:
(1)相似三角形有公共角或对顶角时,公共角或对顶角是最明显的对应角;相似三角形中最大的角(或最小的角)一定是对应角;相似三角形中,一对相等的角是对应角,对应角所对的边是对应边,对应角的夹边是对应边;
(2)相似三角形中,一对最长的边(或最短的边)一定是对应边;对应边所对的角是对应角;对应边所夹的角是对应角.
2、常见的相似三角形的基本图形:
三角形相似的判定,要与三角形全等的判定相比较,把证明三角形全等的思想方法迁移到相似三角形中来;对一些出现频率较高的图形,要善于归纳和记忆;对相似三角形的判定思路要善于总结,形成一整套完整的判定方法.如:
(1)“平行线型”相似三角形。
(2)“相交线型”相似三角形。
(3)“旋转型”相似三角形。
三、相似模型
1.A字、8字模型。
2.共边共角模型(扭屁股模型)。
3.一线三等角模型。
4.倒数模型(较难)
5.圆中的相似。
6.平行线分线段成比例。
类型一、线段比例问题
1.
(构造平行)如图1,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO交AD于F,OE⊥OB交BC边于点E.(1)求证:△ABF∽△COE;(2)当O为AC的中点,=2时,如图2,求的值;(3)当O为AC边中点,=n时,请直接写出的值.
2.如图1
,DE是⊙的直径,点A、C是直径DE上方半圆上的两点,且AO⊥OC.连接AE,CD相交于点F.点B是直径DE下方半圆上的任意一点,连接AB交CD
于点G,连接CB交AE于点H.
(1)求∠ABC的度数;
(2)证明:
△CFH∽△CBG;
(3)若弧DB为半圆的三分之一,把∠AOC绕着点O旋转,使点C、O、B在一直线上时,如图2.①证明FH:BG=1:2;②若⊙O的半径为4,直接写出FH的长.
3.
已知抛物线(a≠0),与x轴从左至右依次相交于A、B两点,与y轴相交于点C,经过点A的直线y=-x+b与抛物线的另一个交点为D.
(1)若点D的横坐标为2,求抛物线的函数解析式;
(2)若在第三象限内的抛物线上有点P,使得以A、B、P为顶点的三角形与△ABC相似,求点P的坐标;
(3)在(1)的条件下,设点E是线段AD上的一点(不含端点),连接BE.一动点Q从点B出发,沿线段BE以每秒1个单位的速度运动到点E,再沿线段ED以每秒
个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?
二、相似比乘积处理方法(逆向和正向分析找解题思路)
1.如果四边形ABCD的对角线交于O,过O作直线OG∥AB交BC于E,交AD于F,交CD的延长线于G,求证:OG2=GE·GF.
2.如图,在平面直角坐标系中,函数(x>0,k是常数)的图像经过A(2,6),B(m,n),其中m>2.过点A作X轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连结AD、DC、CB。
(1)若▲ABD的面积为3,求k的值和直线AB的解析式;
(2)求证:=;
(3)若AD∥BC,求点B的坐标
.
三、构造相似辅助线——A、X字型
1、如图:△ABC中,D是AB上一点,AD=AC,BC边上的中线AE交CD于F。求证:=
2.如图,在Rt▲ACB中,∠ACB=90°,AC=2
cm,AB=4
cm,动点P从点C出发,在BC边上以每秒cm的速度向点B匀速运动,同时动点Q也从点C出发,沿C-A-B以每秒4cm的速度匀速运动,运动时间为t秒(0
(2)设⊙O的面积为s,求s与t的函数关系式;
(3)当点Q在AB上运动时,⊙O与Rt▲ABC的一边相切,求t的值.
3.如图,在等腰直角三角形ABC中,∠BAC=90°,AC=8cm,AD⊥BC于点D,点P从点A出发,沿A→C方向以cm/s的速度运动到点C停止,在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
(1)当点M落在AB上时,x= ;
(2)当点M落在AD上时,x= ;
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
相似类定值问题以及存在性问题
1.如图,四边形ABCD是矩形,点P是对角线AC上一动点(不与A、C重合),连接PB,过点作PE⊥PB,交射线DC于点E,已知AD=3,sin∠BAC=.设AP的长为x.
(1)AB=
;当x=1时,
;
(2)①试探究:否是定值?若是,请求出这个值;若不是,请说明理由;
②连接BE,设▲PBE的面积为S,求S的最小值.
(3)当▲PCE是等腰三角形时.请求出x的值;
(2018年苏州园区一模)
2.如图,正方形ABCD与矩形EFGH在直线l的同侧,边AD、EH在直线l上.保持正方形ABCD不动,并将矩形EFGH以1
cm/s的速度沿DA方向移动,移动开始前点E与点D重合,当矩形EFGH完全穿过正方形ABCD
(即点H与A点重合)时停止移动,设移动时间为t
(s).已知AD=cm,EH=
cm,EF=
cm,连接AF、CG.
(1)矩形EFGH从开始移动到完全穿过正方形ABCD,所用时间为
s;
(2)当AF⊥CG时,求t的值;
3.已知,如图1,直线y=x+3与x轴、y轴分别交于A、C两点,点B在x轴上,点B的横坐标为,抛物线经过A、B、C三点.点D直线AC上方抛物线上任意一点.
(1)求抛物线的函数关系式;
(2)若P为线段AC上一点,且S▲PCD=2S▲PAD,求点P的坐标;
五、证明线段相等
1.在面积为24的△ABC中,矩形DEFG的边DE在AB上运动,点F、G分别在BC、AC上。
(1)若AE=8,DE=2EF,求GF的长;(2)若∠ACB=90°,如图2,线段DM、EN分别为△ADG和△BEF的角平分线,求证:MG=NF;(3)请直接写出矩形DEFG的面积的最大值。
2、在△ABC中,点D从A出发,在AB边上以每秒一个单位的速度向B运动,同时点F从B出发,在BC边上以相同的速度向C运动,过点D作DE∥BC交AC于点E.运动时间为t秒.
(1)若AB=5,BC=6,当t为何值时,四边形DFCE为平行四边形;(2)连接AF、CD.若BD=DE,求证:∠BAF=∠BCD;(3)AF交DE于点M,在DC上取点N,使MN∥AC,连接FN.
①求证:=;②若AB=5,BC=6,AC=4,当MN=FN时,请直接写出t的值.
3.如图,Rt▲ABC中,∠A=90°,以AB为直径的⊙O交BC边交于点E,
EF⊥AB,垂足为F.D为AC的中点,连结BD交EF于G.
(1)求证:ED是⊙O的切线;
(2)求证:EG=FG;
(3)若DG=DA=4,求O的半径.
最值问题
1.如图,在Rt▲ABC中,∠A=30°,AC=8,以C为圆心,4为半径作⊙C.
(1)试判断⊙C与AB的位置关系,并说明理由;
(2)点F是⊙C上一动点,点D在AC上且CD=2,试说明▲FCD
:▲ACF;
(3)点E是AB边上任意一点,在(2)的情况下,试求出EF+FA的最小值.
2.如图,抛物线y=a2-3ax+c(a≠0)与x轴交于A,B两点,交y轴于点C,其中A(-1,0),C(0,3).
求抛物线的解析式
点P是线段BC上方抛物线上一动点(不与B,C重合),过点P作PD⊥x轴,垂足为D,交BC于点E,作PF⊥直线BC于点F,设点P的横坐标为x,△PEF的周长记为l,求l关于x的函数关系式,并求出l的最大值及此时点P的坐标
点H是直线AC上一点,该抛物线的对称轴上一动点G,连接OG,GH,则两线段OG,GH的长度之和的最小值等于______,此时点G的坐标为_____(直接写出答案。)
3.如图,Rt△ABC中.∠BAC=90°,AB=1,AC=2.点D,E分别是边BC.AC上的动点,
则DA+DE的最小值为
七、
相似基本模型应用
1.如图,四边形ABCD的对角线交于点O,且AB∥CD有以下四个结论:
①▲AOB:▲COD
②▲AOD:▲ACB
③S▲DOC:S▲AOD=DC:AB
④S▲AOD=S▲BOC
其中,始终正确的有(
)
A.
1个
B.
2个
C.
3个
D.
4个
2.如图,己知Rt▲ABC的直角边AC与Rt▲DEF的直角边DF在同一条直线上,且AC=60cm,
BC=45cm,
DE=6cm,
EF=8cm.现将点C与点F重合,再以4
cm/s的速度沿CA方向移动▲DEF;同时,点P从点A出发,以5
cm/s的速度沿AB方向移动,设移动时间为t
(s).以点P为圆心,3t
(cm)长为半径的⊙P与AB相交于点M、N.当点F与点A重合时,▲DEF与点P同时停止移动.在移动的过程中,
(1)连接ME,当ME∥AC时,t=
s;
(2)连接NF,当NF平分DE时,求t的值;
3.在Rt▲ABC中,∠C=90°,Rt▲ABC绕点A顺时针旋转到Rt▲ADE的
位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.
如图1,若点F与点A重合,求证:AC=BC;
(2)若∠DAF=∠DBA,
①如图2,当点F在线段CA的延长线上时,判断线段AF与线段BE的数量关系,并说明理由;
(母子相似)②当点F在线段CA上时,设BE=x,请用含x的代数式表示线段AF.
八、与圆有关的相似
1.(隐圆相似)如图,在Rt▲ABC中,∠ACB=90°,BC=6,AC=8.点D、E分别是边AB、BC的中点,连接DE,将▲BDE绕点B按顺时针方向旋转一定角度(这个角度小于90?)后,点D的对应点D“和点E的对应点E”以及点A三个点在一直线上,连接CE“,则CE“=
.
2.(最值问题)如图,AB是半⊙O的直径,且AB=8.点C是半⊙O上的一个动点(不与点A、B重合),过点C作CD⊥AB,垂足为D.设AC=x,AD=y,则x-y的最大值等于
.
3.(最值问题)如图,在▲ABC中,∠ACB=90°,BC=12,AC=9,以点C为圆心,6为半径的圆上有一个动点D.连接AD、BD、CD,则AD+BD的最小值是
.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
