三角形的应用
图片预览



文档简介
(共11张PPT)
回顾与思考
在《小车下滑的时间》 中:
支撑物的高度h和小车下滑的时间t都在变化,
它们都是变量.
其中小车下滑的时间t随支撑物的高度h的变化而变化,
支撑物的高度h是自变量
小车下滑的时间t是因变量
练一练
婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,6周岁、10周岁时的体重分别大约是1周岁时的2倍、3倍。
年龄 刚出生 6个月 1周岁 2周岁 6周岁 10周岁
体重/千克
根据表中的数据,说一说儿童从出生到10周岁之间体重是怎样随着年龄的增长而变化的。
2)某婴儿在出生时的体重是3.5千克,请把他在发育过程中的体重情况填入下表:
1)上述哪些量在发生变化?自变量和因变量各是什么?
发生变化的量是:
体重和时间
自变量是:
因变量是:
时间
体重
3.5
7.0
10.5
14.0
21.0
31.5
想一想
A
B
C
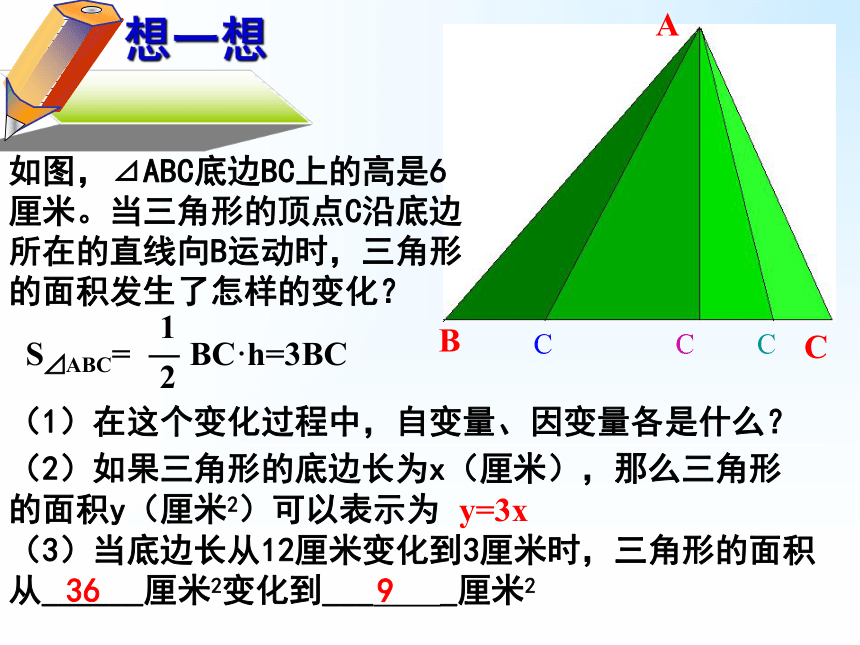
如图,⊿ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在的直线向B运动时,三角形的面积发生了怎样的变化?
C
C
S⊿ABC= ― BC·h=3BC
1
2
C
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如果三角形的底边长为x(厘米),那么三角形的面积y(厘米2)可以表示为
y=3x
(3)当底边长从12厘米变化到3厘米时,三角形的面积从______厘米2变化到___ _厘米2
36
9
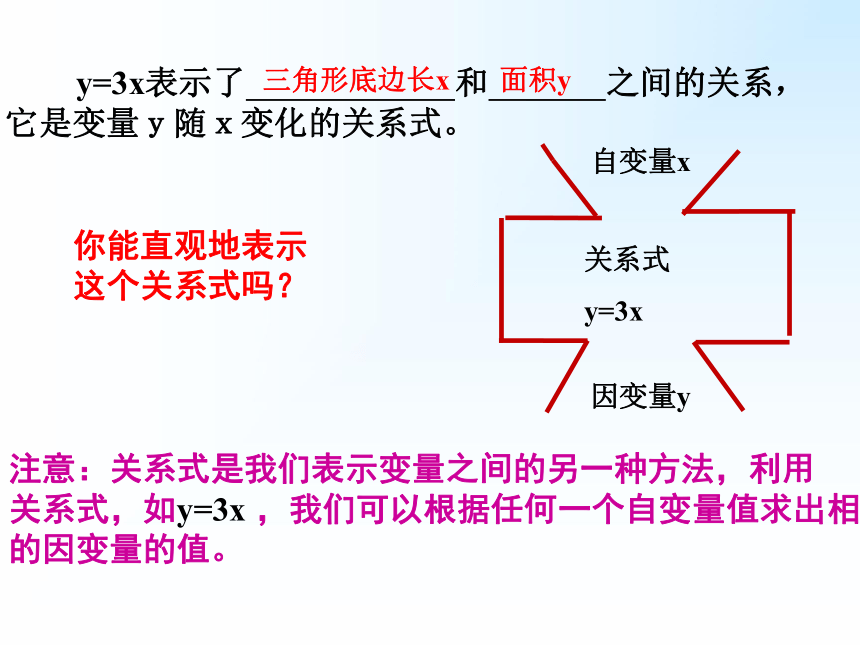
y=3x表示了 和 之间的关系,它是变量y随x变化的关系式。
你能直观地表示这个关系式吗?
自变量x
关系式
y=3x
因变量y
三角形底边长x
面积y
注意:关系式是我们表示变量之间的另一种方法,利用
关系式,如y=3x ,我们可以根据任何一个自变量值求出相应
的因变量的值。
V=πr2h/3
r
h
做一做
1、 如图,圆锥的高度是4厘米,当圆锥的的底面半径由小到大变化时,圆锥的体积也随之发生了变化。
4厘米
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如果圆锥底面半径为r(厘米),那么圆锥的体积v(厘米3)与r的关系式为______________
V=4πr2/3
(3)当底面半径由1厘米变化到10厘米时,圆锥的体积由 厘米3变化到 厘米3 。
4π/3
400π/3
2、 如图,圆锥的底面半径是2厘米,当圆锥的高由小到大变化时,圆锥的体积也随之变化。
2㎝
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如果圆锥的高为h(厘米),那么圆锥的体积v(厘米3)与h之间的关系式为 .
(3)当高由1厘米变化到10厘米时,
圆锥的体积由 厘米3变化到 厘米3
V=4πh/3
4π/3
40π/3
随堂练习
自变量d
T=10-d/150
因变量T
1。在地球某地,温度T(C)
与高度d(m)的关系可以近
似地用T=10-d/150来表示,
根据这个关系式,当d的值
分别是0,200,400,600,
800,1000时,计算相应的
T值,并用表格表示所得结果。
高度d/m 0 200 400 600 800 1000
温度T/°C
10.00
8.67
7.33
6.00
4.67
3.33
1 本节主要是探索了图形中的变量关系
2 能用关系式表示变量之间的关系
3 能根据关系式求值。
作业P170 1,2题
回顾与思考
在《小车下滑的时间》 中:
支撑物的高度h和小车下滑的时间t都在变化,
它们都是变量.
其中小车下滑的时间t随支撑物的高度h的变化而变化,
支撑物的高度h是自变量
小车下滑的时间t是因变量
练一练
婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,6周岁、10周岁时的体重分别大约是1周岁时的2倍、3倍。
年龄 刚出生 6个月 1周岁 2周岁 6周岁 10周岁
体重/千克
根据表中的数据,说一说儿童从出生到10周岁之间体重是怎样随着年龄的增长而变化的。
2)某婴儿在出生时的体重是3.5千克,请把他在发育过程中的体重情况填入下表:
1)上述哪些量在发生变化?自变量和因变量各是什么?
发生变化的量是:
体重和时间
自变量是:
因变量是:
时间
体重
3.5
7.0
10.5
14.0
21.0
31.5
想一想
A
B
C
如图,⊿ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在的直线向B运动时,三角形的面积发生了怎样的变化?
C
C
S⊿ABC= ― BC·h=3BC
1
2
C
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如果三角形的底边长为x(厘米),那么三角形的面积y(厘米2)可以表示为
y=3x
(3)当底边长从12厘米变化到3厘米时,三角形的面积从______厘米2变化到___ _厘米2
36
9
y=3x表示了 和 之间的关系,它是变量y随x变化的关系式。
你能直观地表示这个关系式吗?
自变量x
关系式
y=3x
因变量y
三角形底边长x
面积y
注意:关系式是我们表示变量之间的另一种方法,利用
关系式,如y=3x ,我们可以根据任何一个自变量值求出相应
的因变量的值。
V=πr2h/3
r
h
做一做
1、 如图,圆锥的高度是4厘米,当圆锥的的底面半径由小到大变化时,圆锥的体积也随之发生了变化。
4厘米
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如果圆锥底面半径为r(厘米),那么圆锥的体积v(厘米3)与r的关系式为______________
V=4πr2/3
(3)当底面半径由1厘米变化到10厘米时,圆锥的体积由 厘米3变化到 厘米3 。
4π/3
400π/3
2、 如图,圆锥的底面半径是2厘米,当圆锥的高由小到大变化时,圆锥的体积也随之变化。
2㎝
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如果圆锥的高为h(厘米),那么圆锥的体积v(厘米3)与h之间的关系式为 .
(3)当高由1厘米变化到10厘米时,
圆锥的体积由 厘米3变化到 厘米3
V=4πh/3
4π/3
40π/3
随堂练习
自变量d
T=10-d/150
因变量T
1。在地球某地,温度T(C)
与高度d(m)的关系可以近
似地用T=10-d/150来表示,
根据这个关系式,当d的值
分别是0,200,400,600,
800,1000时,计算相应的
T值,并用表格表示所得结果。
高度d/m 0 200 400 600 800 1000
温度T/°C
10.00
8.67
7.33
6.00
4.67
3.33
1 本节主要是探索了图形中的变量关系
2 能用关系式表示变量之间的关系
3 能根据关系式求值。
作业P170 1,2题
