人教版八年级数学上学期《12.3 角的平分线的性质》 同步练习(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上学期《12.3 角的平分线的性质》 同步练习(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 139.6KB | ||
| 资源类型 | 教案 | ||
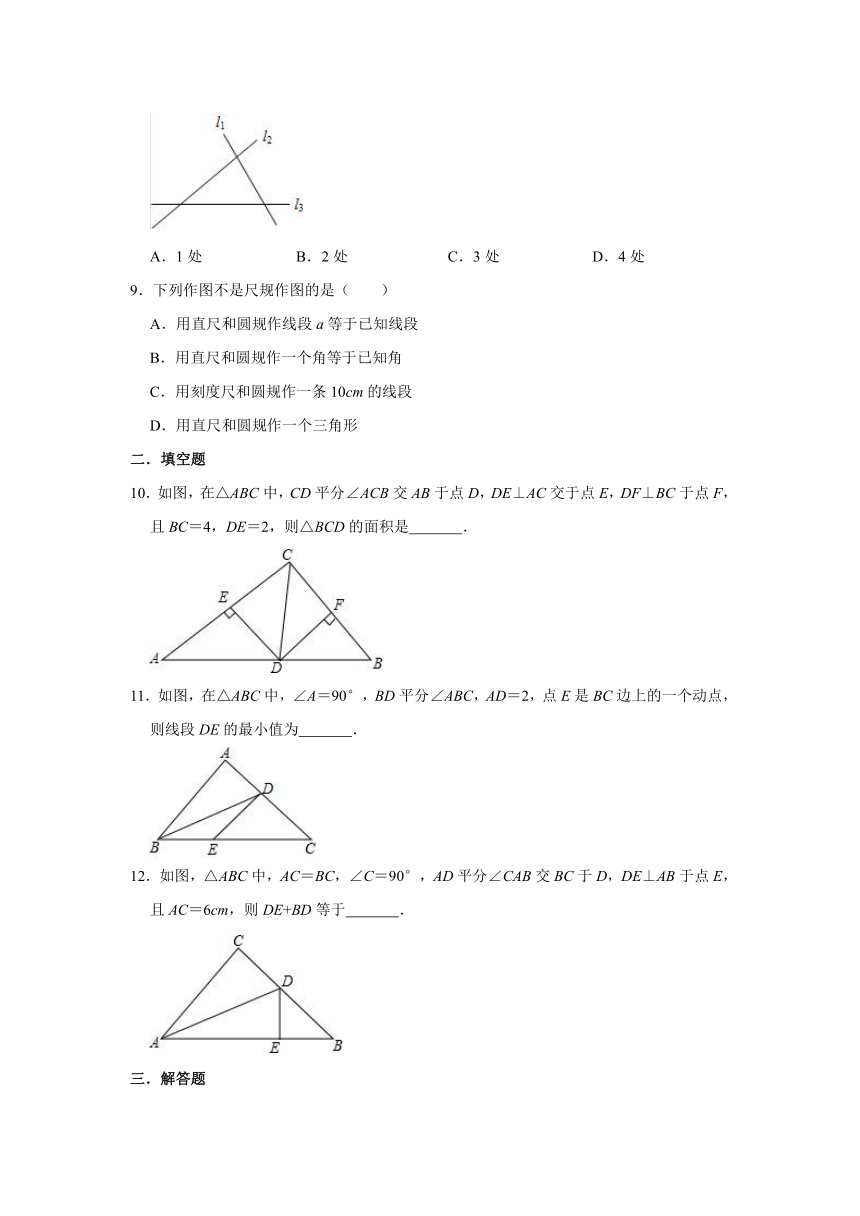
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-14 00:00:00 | ||
图片预览


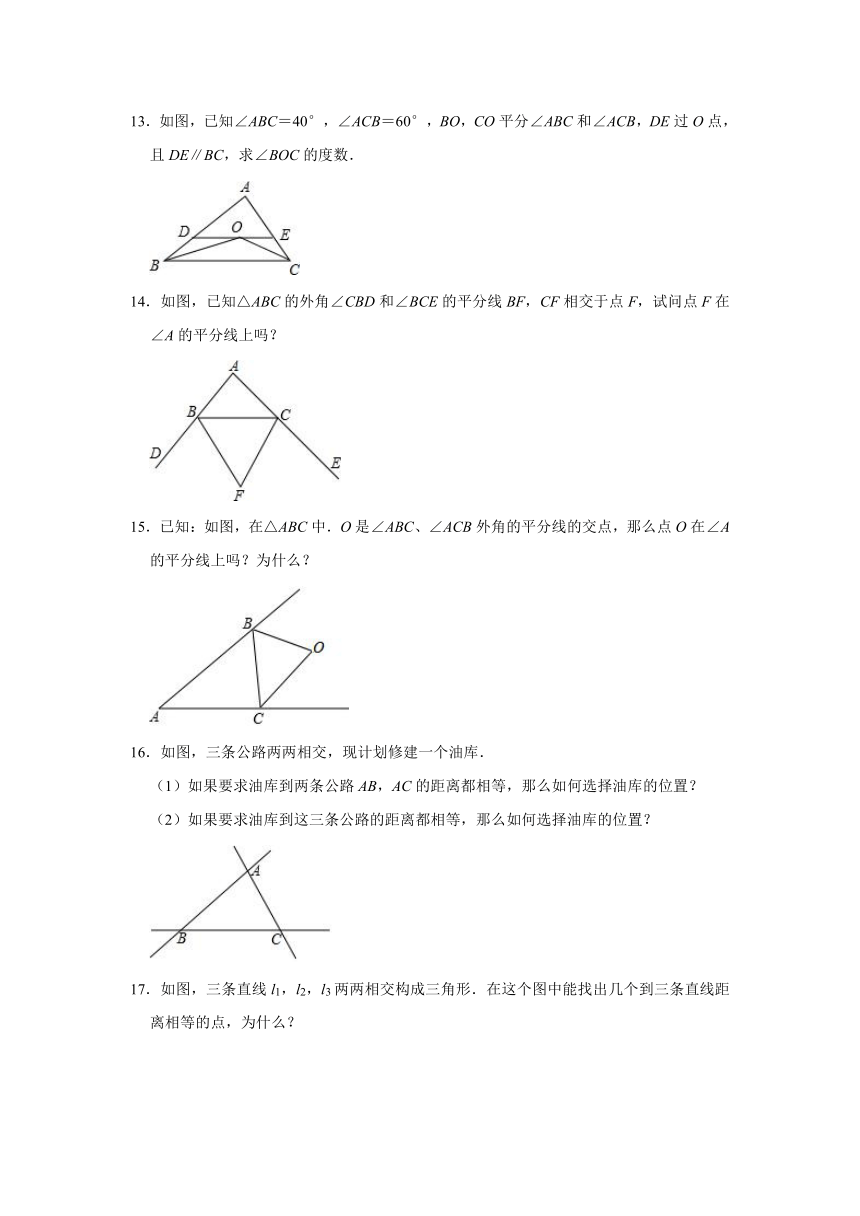
文档简介
12.3
角的平分线的性质
一.选择题
1.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=10,DE=2,AB=6,则AC长是( )
A.3
B.4
C.6
D.5
2.如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A,B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC.若OA=5,AB=6,则点B到AC的距离为( )
A.5
B.
C.4
D.
3.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A.30°
B.35°
C.45°
D.60°
4.如图,点O是△ABC的两外角平分线的交点,下列结论:①OB=OC;②点O到AB、AC的距离相等;③点O到△ABC的三边的距离相等;④点O在∠A的平分线上.其中结论正确的个数是( )
A.1
B.2
C.3
D.4
5.如图:△ABC的两个外角平分线交于点P,则下列结论正确的是( )
①PA=PC②BP平分∠ABC③P到AB,BC的距离相等
④BP平分∠APC.
A.①②
B.①④
C.③②
D.③④
6.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,∠C的平分线与∠ABC的外角的平分线交于E点,则∠AEB是( )
A.50°
B.45°
C.40°
D.35°
7.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1
B.1:2:3
C.2:3:4
D.3:4:5
8.如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则供选择的地址有( )
A.1处
B.2处
C.3处
D.4处
9.下列作图不是尺规作图的是( )
A.用直尺和圆规作线段a等于已知线段
B.用直尺和圆规作一个角等于已知角
C.用刻度尺和圆规作一条10cm的线段
D.用直尺和圆规作一个三角形
二.填空题
10.如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是
.
11.如图,在△ABC中,∠A=90°,BD平分∠ABC,AD=2,点E是BC边上的一个动点,则线段DE的最小值为
.
12.如图,△ABC中,AC=BC,∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于点E,且AC=6cm,则DE+BD等于
.
三.解答题
13.如图,已知∠ABC=40°,∠ACB=60°,BO,CO平分∠ABC和∠ACB,DE过O点,且DE∥BC,求∠BOC的度数.
14.如图,已知△ABC的外角∠CBD和∠BCE的平分线BF,CF相交于点F,试问点F在∠A的平分线上吗?
15.已知:如图,在△ABC中.O是∠ABC、∠ACB外角的平分线的交点,那么点O在∠A的平分线上吗?为什么?
16.如图,三条公路两两相交,现计划修建一个油库.
(1)如果要求油库到两条公路AB,AC的距离都相等,那么如何选择油库的位置?
(2)如果要求油库到这三条公路的距离都相等,那么如何选择油库的位置?
17.如图,三条直线l1,l2,l3两两相交构成三角形.在这个图中能找出几个到三条直线距离相等的点,为什么?
18.如图,OM为∠AOB的平分线,点P是射线OM上的一点,PA⊥OA于点A,PB⊥OB于点B,分别度量PA,PB的长度,并判断它们的数量关系;如果在射线OM上再取几个不同位置的点P.然后向角的两边作垂线段,刚才的数量关系还存在吗?
19.如图,∠ABC的平分线与∠ACB的外角平分线相交于点D,连接AD.求证:AD是∠BAC的外角平分线.
参考答案与试题解析
一.选择题
1.
B.
2.
B.
3.
B.
4.
C.
5.
C.
6.
B.
7.
C.
8.
D.
9.
C.
二.填空题
10.
4.
11.
2.
12.
6cm.
三.解答题
13.∵∠ABC=40°,∠ACB=60°,BO,CO平分∠ABC和∠ACB,
∴∠OBC+∠OCB=(∠ACB+∠ABC)=50°;
∴∠BOC=180°﹣50°=130°.
14.如图,过点F分别作FM⊥AB,FN⊥AC,FG⊥BC,垂足分别为M、N、G,
∵BF、CF分别平分∠CBD和∠BCE,
∴FM=FG=FN,
∴F在∠A的平分线上.
15.点O在∠C的平分线上.
理由如下:O作OD⊥AB于D,作OE⊥AC于E,作OF⊥BC于F,
∵O是∠ABC和∠ACB外角的平分线的交点,
∴OD=OF,OE=OF,
∴OF=OD=OE,
∴点O在∠A的平分线上.
16.(1)如图,加油站的位置在直线MN或直线EF上.
(2)如图,点P1,P2,P3,P4即为所求.
17.作三条直线l1,l2,l3两两相交构成的三角形的内角平分线和外角平分线,它们有4个交点,根据角平分线的性质得每个交点到三条直线的距离相等,
所以在这个图中能找出4个到三条直线距离相等的点.
18.∵OM是∠AOB的平分线,AP⊥OA,PB⊥OB,
∴PA=PB,
所以在射线OM上再取几个不同位置的点P.然后向角的两边作垂线段,刚才的数量关系还存在.
19.证明:作DE⊥BA交BA的延长线于E,DF⊥AC于F,DG⊥BH于G,
∵DB、DC分别是∠ABC的平分线与∠ACB的外角平分线,
∴DE=DG,DF=DG,
∴DE=DF,又DE⊥BA,DF⊥AC,
∴AD是∠BAC的外角平分线.
角的平分线的性质
一.选择题
1.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=10,DE=2,AB=6,则AC长是( )
A.3
B.4
C.6
D.5
2.如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A,B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC.若OA=5,AB=6,则点B到AC的距离为( )
A.5
B.
C.4
D.
3.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A.30°
B.35°
C.45°
D.60°
4.如图,点O是△ABC的两外角平分线的交点,下列结论:①OB=OC;②点O到AB、AC的距离相等;③点O到△ABC的三边的距离相等;④点O在∠A的平分线上.其中结论正确的个数是( )
A.1
B.2
C.3
D.4
5.如图:△ABC的两个外角平分线交于点P,则下列结论正确的是( )
①PA=PC②BP平分∠ABC③P到AB,BC的距离相等
④BP平分∠APC.
A.①②
B.①④
C.③②
D.③④
6.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,∠C的平分线与∠ABC的外角的平分线交于E点,则∠AEB是( )
A.50°
B.45°
C.40°
D.35°
7.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1
B.1:2:3
C.2:3:4
D.3:4:5
8.如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则供选择的地址有( )
A.1处
B.2处
C.3处
D.4处
9.下列作图不是尺规作图的是( )
A.用直尺和圆规作线段a等于已知线段
B.用直尺和圆规作一个角等于已知角
C.用刻度尺和圆规作一条10cm的线段
D.用直尺和圆规作一个三角形
二.填空题
10.如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是
.
11.如图,在△ABC中,∠A=90°,BD平分∠ABC,AD=2,点E是BC边上的一个动点,则线段DE的最小值为
.
12.如图,△ABC中,AC=BC,∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于点E,且AC=6cm,则DE+BD等于
.
三.解答题
13.如图,已知∠ABC=40°,∠ACB=60°,BO,CO平分∠ABC和∠ACB,DE过O点,且DE∥BC,求∠BOC的度数.
14.如图,已知△ABC的外角∠CBD和∠BCE的平分线BF,CF相交于点F,试问点F在∠A的平分线上吗?
15.已知:如图,在△ABC中.O是∠ABC、∠ACB外角的平分线的交点,那么点O在∠A的平分线上吗?为什么?
16.如图,三条公路两两相交,现计划修建一个油库.
(1)如果要求油库到两条公路AB,AC的距离都相等,那么如何选择油库的位置?
(2)如果要求油库到这三条公路的距离都相等,那么如何选择油库的位置?
17.如图,三条直线l1,l2,l3两两相交构成三角形.在这个图中能找出几个到三条直线距离相等的点,为什么?
18.如图,OM为∠AOB的平分线,点P是射线OM上的一点,PA⊥OA于点A,PB⊥OB于点B,分别度量PA,PB的长度,并判断它们的数量关系;如果在射线OM上再取几个不同位置的点P.然后向角的两边作垂线段,刚才的数量关系还存在吗?
19.如图,∠ABC的平分线与∠ACB的外角平分线相交于点D,连接AD.求证:AD是∠BAC的外角平分线.
参考答案与试题解析
一.选择题
1.
B.
2.
B.
3.
B.
4.
C.
5.
C.
6.
B.
7.
C.
8.
D.
9.
C.
二.填空题
10.
4.
11.
2.
12.
6cm.
三.解答题
13.∵∠ABC=40°,∠ACB=60°,BO,CO平分∠ABC和∠ACB,
∴∠OBC+∠OCB=(∠ACB+∠ABC)=50°;
∴∠BOC=180°﹣50°=130°.
14.如图,过点F分别作FM⊥AB,FN⊥AC,FG⊥BC,垂足分别为M、N、G,
∵BF、CF分别平分∠CBD和∠BCE,
∴FM=FG=FN,
∴F在∠A的平分线上.
15.点O在∠C的平分线上.
理由如下:O作OD⊥AB于D,作OE⊥AC于E,作OF⊥BC于F,
∵O是∠ABC和∠ACB外角的平分线的交点,
∴OD=OF,OE=OF,
∴OF=OD=OE,
∴点O在∠A的平分线上.
16.(1)如图,加油站的位置在直线MN或直线EF上.
(2)如图,点P1,P2,P3,P4即为所求.
17.作三条直线l1,l2,l3两两相交构成的三角形的内角平分线和外角平分线,它们有4个交点,根据角平分线的性质得每个交点到三条直线的距离相等,
所以在这个图中能找出4个到三条直线距离相等的点.
18.∵OM是∠AOB的平分线,AP⊥OA,PB⊥OB,
∴PA=PB,
所以在射线OM上再取几个不同位置的点P.然后向角的两边作垂线段,刚才的数量关系还存在.
19.证明:作DE⊥BA交BA的延长线于E,DF⊥AC于F,DG⊥BH于G,
∵DB、DC分别是∠ABC的平分线与∠ACB的外角平分线,
∴DE=DG,DF=DG,
∴DE=DF,又DE⊥BA,DF⊥AC,
∴AD是∠BAC的外角平分线.
