3.2代数式的值课件

(共26张PPT)
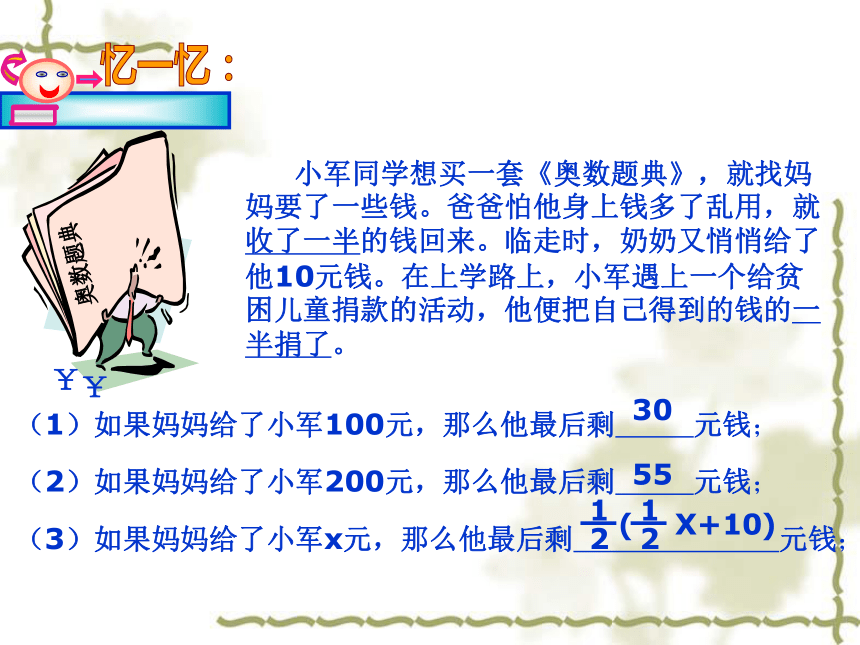
小军同学想买一套《奥数题典》，就找妈妈要了一些钱。爸爸怕他身上钱多了乱用，就收了一半的钱回来。临走时，奶奶又悄悄给了他10元钱。在上学路上，小军遇上一个给贫困儿童捐款的活动，他便把自己得到的钱的一半捐了。
￥
￥
（1）如果妈妈给了小军100元，那么他最后剩 元钱；
（2）如果妈妈给了小军200元，那么他最后剩 元钱；
（3）如果妈妈给了小军x元，那么他最后剩 元钱；
30
55
2
1
X+10
(
)
2
1
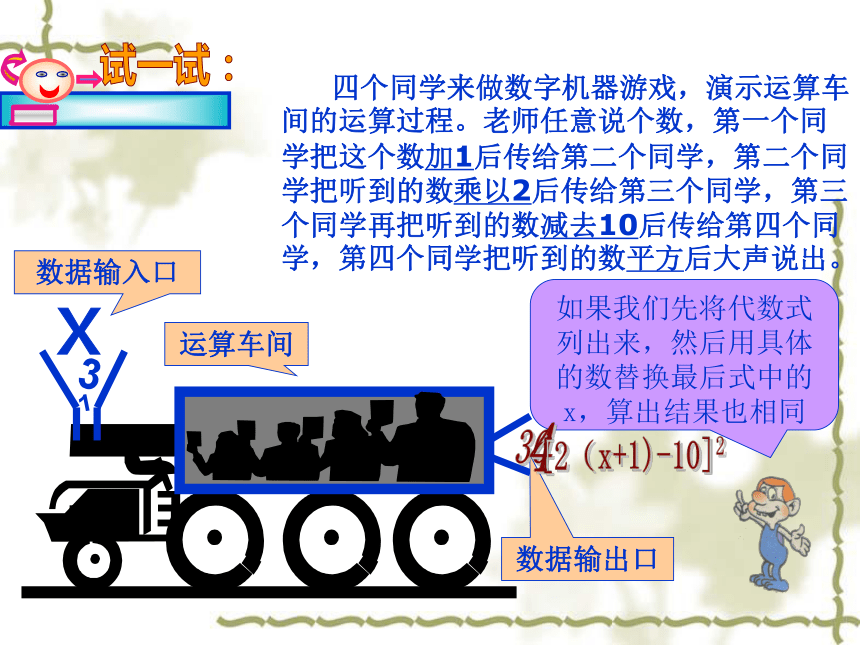
数据输入口
运算车间
数据输出口
四个同学来做数字机器游戏，演示运算车间的运算过程。老师任意说个数，第一个同学把这个数加1后传给第二个同学，第二个同学把听到的数乘以2后传给第三个同学，第三个同学再把听到的数减去10后传给第四个同学，第四个同学把听到的数平方后大声说出。
如果我们先将代数式列出来，然后用具体 的数替换最后式中的 x，算出结果也相同
用数值代替代数式里的字母，按照代数式中的运算关系计算得出的结果，叫做代数式的值。
例1.当x=2，y=-3时，求代数式 x(x-y) 的值
解：当x=2，y=-3时
x(x-y) = 2×[2-(-3)]
=2 ×5
=10
由例题可以看出
求代数式的值的解题格式: “当 …… 时，原式=”
求代数式的值的步骤:
(1)写出条件：当……时
(2)抄写代数式
(3)代入数值
(4)计算
例2:求代数式x2-1的值
(1) x=-2时， (2) x= 时，
解:(1)当x=-2时
x2-1 = (-2)2-1
=4-1
=3
1
2
(2)当x= 时
x2-1= ( )2-1
= -1
=-
1
2
1
2
1
4
3
4
从例题可以看到:
(1) 求代数式的值，就是把代数式中的字母用指定的数据来代替（代入），原式中的运算符号及数字不能改变；然后按照代数式中指定的运算来进行计算（计算）。
(2) 代数式中的字母用负数或分数来代替时，要注意添上括号。
(3)数字与数字相乘，要写“×”号，因此，如果原代数式中有乘法运算，当其中的字母用数字在替代时，要恢复“×”号。
例3: 每个练习本的价格是0.8元,买n个练习本要花多少钱 买10个,20个要花多少钱？
解：由题意得：买n个练习本要花0.8n元。
当n=10时，0.8×10=8 (元)
当n=20时, 0.8×20=16(元)
答：买n个练习本要花0.8n元，
买10个，20个各要花8元，16元。
从例题可以看到:
代数式的值由代数式中的字母的取值确定，同一个代数式若字母的取值不同，所得的值也可能不同。
1.当a=3,b= -1时，求下列各代数式的值。
(1) (a+b) , (2) a + 2ab+b , (3) (a - b) , (4) a - 2ab+b
课堂练习
解:(1) 当a=3,b= -1时，
(a+b)
=[3+(-1)]
= 2
=4
(2) 当a=3,b= -1时，
a +2ab+b
=3 +2×3× (-1)+(-1)
=9+(-6)+1
= 4
2、当a=2，b=-1，c=-3时，求下列代数式的值：
(1) b2-4ac
(2) a2+b2+c2+2ab+2bc+2ac
(3) (a+b+c)2
解：（1）当a=2，b=-1，c=-3时
b2-4ac=-1 2-4×2 ×-3
=1+24=25
( )
( )
课堂练习
观察(2)(3)两题的结果，你有什么想法？
a2+b2+c2+2ab+2bc+2ac
解：（2）当a=2，b=-1，c=-3时
=22+(-1)2+(-3)2+2×2×(-1)+2×(-1)×
(-3)+2×2×(-3)
=4+1+9-4+6-12=4
解：依题意,得x＝-2，y＝±3，b/a＝1，
3.X是1/2的倒数的相反数，绝对值为3的数是y，a、b互为相反数(a≠0)，且|m-2|+(n-1)2=0,
求x2-2mn+y-b/a的值：
∵ |m-2|≥0,(n-1)2 ≥ 0,
且|m-2|+(n-1)2=0
当y=3时,原式＝(－2)2－2×2×1+3-1=2,
∴m-2=0,n-1=0, ∴m=2,n=1
当y=-3时,原式＝(－2)2－2×2×1-3-1=-4,
∴ x2-2mn+y-b/a的值为2或-4.
4.按右边图示的程序计算，若开始输入的n值为2，则最后输出的结果是 。
231
输入n
计算 的值
＞200
输出结果
yes
no
试一试
1. 若梯形的上底为a，下底为b，高为h，则梯形的面积为_______________,
当a=2cm，b=3cm,h=4cm时，s梯=____________.
__
S梯=
1
2
(a+b)h
10cm
2.某企业去年的年产值为a亿元，今年比去年增长了10%，那么今年的年产值是__________亿元,如果明年还能按这个速度增长,该企业明年的年产值将能达到 ____________亿元,如果去年的年产值是2亿元，那么预计明年的年产值是_______亿元。
(1+10%)a
(1+10%) a
2.42
3.当x-y=1,x+y=7时,求代数式15(x-y)-9+3(x+y) 的值。
解：当x-y=1,x+y=7时，
15(x-y)-9+3(x+y)
=15×1-9+3×7=27
用整体思想求代数式的值
变式1. 若3x -2x=7,
求6x -4x-2的值
变式2. 当x=2时,(a+b)x3-9的值为7,当x=-2时,(a+b)x3-9的值为多少？
变式3. 已知a+b=3ab,
用换元思想求代数式的值
想一想
当 —— =2 时，代数式 —— 的值是多少 代数式 —— 的值是多少
5xy
6x-3y
15xy
10xy
2x-y
2x-y
测得某弹簧的长度y(cm)与挂重x(kg)有下表关系(该弹簧挂重不得超过20kg):
X(千克) 0 1 2 3 …
Y(厘米) 4 4.2 4.4 4.6 …
(1)写出y与x的关系式:
(2)计算当弹簧的长度为5.6厘米的弹簧挂重.
这节课我们主要学习了
1、代数式的值的概念
2、计算代数式的值的方法
3、怎样运用代数式的值解决生活中的问题
注 意
在解决实际问题时，一定要仔细弄清题意，先列出一个正确的代数式。
(1) 格式: “ 当 …… 时 ，原式=”
(2) 代入时，数字要代入对应的字母的位置去；
(3) 在求值时，原来省略的乘号要添上
(4) 若代入的是负数或分数，必须加上括号。
我们在求“代数式的值”时，有哪些是需要我们注意的呢？
　
2 . 当a=4，b=-2时，求下列代数式的值： (1)(a+b)2； (2)(a-b)2?
(3)a2+b2； (4)a2-b2?
三、例题
解(1) a=4，b=-2时
(a+b)2 = [4+(-2)]2
=2 2
=4
(2) a=4，b=-2时
(a-b)2 = [4-(-2)]2
=6 2
=36
(3) a=4，b=-2时
a2+b2 = 42+(-2)2
=16+4
=20
(4) a=4，b=-2时
a2-b2 = 42- (-2) 2
=16-4
=12
从这个例题可以看到：当a、b的值相同时，
(a+b)2
a2+b2
值并不相同，所以不能把这两个代数式混为一谈。
同样：当a、b的值相同时，
(a-b)2
a2-b2
值也不相同，所以也不能把这两个代数式混为一谈。