沪科版(2012)初中数学九年级上 册 21.3.2 由二次函数的图象认识一元二次不等式的解集 教案
文档属性
| 名称 | 沪科版(2012)初中数学九年级上 册 21.3.2 由二次函数的图象认识一元二次不等式的解集 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 479.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-16 10:58:15 | ||
图片预览

文档简介
《由二次函数的图象认识一元二次不等式的解集》教学设计
一、教学内容:
沪科版数学九(上)第21.3二次函数与一元二次方程P33“阅读与思考”.
二、教学目标:
1.经历探索二次函数与一元二次不等式之间关系的过程,体会不等式与函数之间的联系;
2.经历用二次函数的图象求一元二次不等式的解集的过程,获得用图象法求解一元二次不等式的体验;
3.引导学生认识事物的部分与整体之间的关系,发展学生的辩证思维能力。
三、重点难点
1.教学重点是三种类型的一元二次不等式图象解法。
2.教学难点是二次不等式、二次方程和二次函数三者关系的有机联系。数形结合和分类转化等数学思想的理解和运用。
四、教具准备:电教多媒体、几何画板软件、绘有空白格点图的稿纸
五、教学活动:
(一)复习回顾:
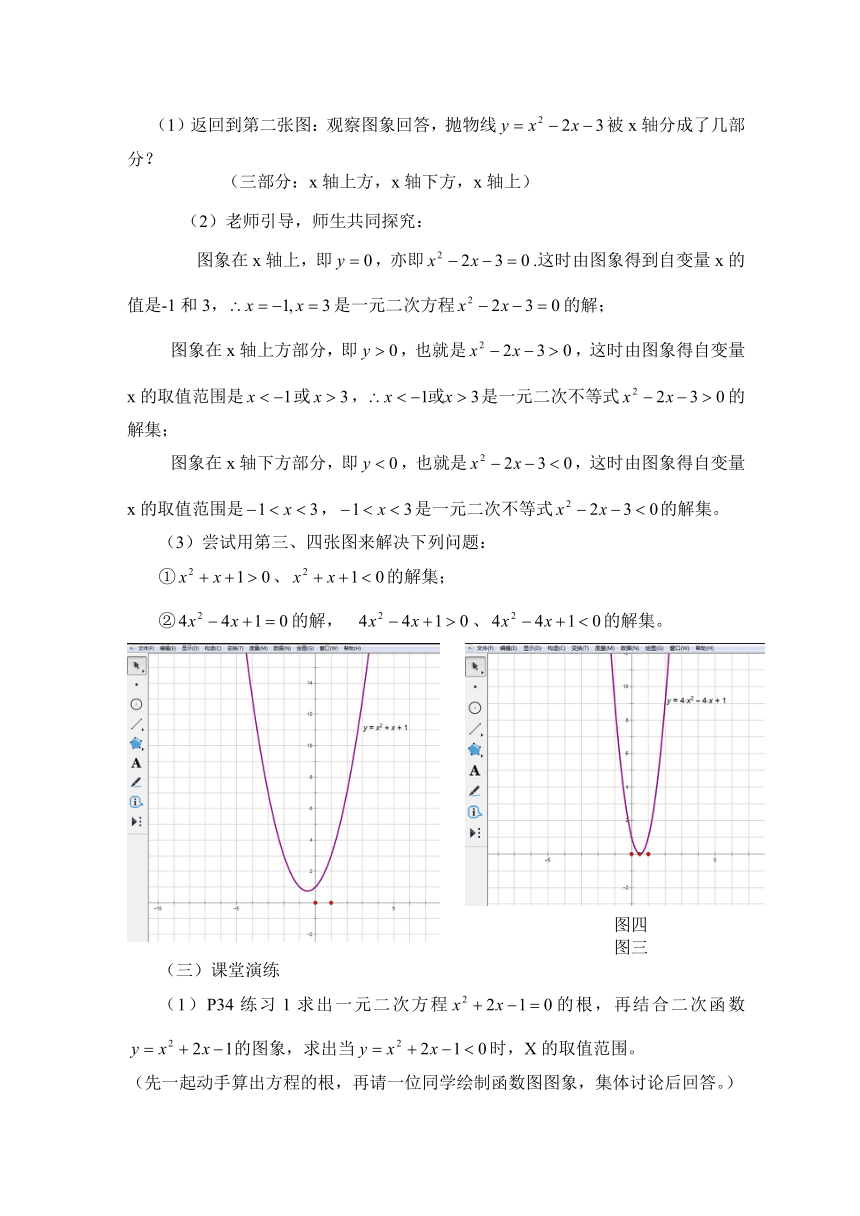
(1)我们在第12章时学过一次函数与一次方程、一次不等式之间的关系,请利用几何画板求解:
,,.(一生绘制函数图象,提问学生回答。)
图一
图二
(2)判断下列二次函数的图象与x轴有无交点,说明理由。
(1),
(2),
(3).
同学们先通过计算来说明,再找三名学生用几何画板绘制函数图象验证。
(二)引入新课:
(1)返回到第二张图:观察图象回答,抛物线被x轴分成了几部分?
(三部分:x轴上方,x轴下方,x轴上)
(2)老师引导,师生共同探究:
图象在x轴上,即,亦即.这时由图象得到自变量x的值是-1和3,是一元二次方程的解;
图象在x轴上方部分,即,也就是,这时由图象得自变量x的取值范围是或,是一元二次不等式的解集;
图象在x轴下方部分,即,也就是,这时由图象得自变量x的取值范围是,是一元二次不等式的解集。
(3)尝试用第三、四张图来解决下列问题:
①、的解集;
②的解,、的解集。
图四
图三
(三)课堂演练
(1)P34练习1求出一元二次方程的根,再结合二次函数的图象,求出当时,X的取值范围。
(先一起动手算出方程的根,再请一位同学绘制函数图图象,集体讨论后回答。)
(2)P34练习2结合函数的图象,求:
①
的解集;
②
的解集。
图五
图六
(四)课堂小结
这节课你们学到了什么?
教师鼓励学生积极回答,答不完整的没有关系,其它同学补充。以此培养学生的口头表达能力,归纳概括能力。并用多媒体把学生的归纳用一张表展示出来,告诉学生不必死记硬背,而是掌握其数形结合的基本原理和基本步骤。
一元二次不等式与一元二次方程及一元二次函数的关系
一元二次函数的图象
一元二次方程的根
有两实根
有两相等的实根
无实根
一元二次不等式的解集
全体实数
不等式的解集
无解
无解
解一元二次不等式的步骤:求根——画图——找解
(告诉学生,在非常熟悉的情况下可省略第二步,但应做到“成图在胸”)
(五)布置作业
P35
习题21.3第8、9两题。
一、教学内容:
沪科版数学九(上)第21.3二次函数与一元二次方程P33“阅读与思考”.
二、教学目标:
1.经历探索二次函数与一元二次不等式之间关系的过程,体会不等式与函数之间的联系;
2.经历用二次函数的图象求一元二次不等式的解集的过程,获得用图象法求解一元二次不等式的体验;
3.引导学生认识事物的部分与整体之间的关系,发展学生的辩证思维能力。
三、重点难点
1.教学重点是三种类型的一元二次不等式图象解法。
2.教学难点是二次不等式、二次方程和二次函数三者关系的有机联系。数形结合和分类转化等数学思想的理解和运用。
四、教具准备:电教多媒体、几何画板软件、绘有空白格点图的稿纸
五、教学活动:
(一)复习回顾:
(1)我们在第12章时学过一次函数与一次方程、一次不等式之间的关系,请利用几何画板求解:
,,.(一生绘制函数图象,提问学生回答。)
图一
图二
(2)判断下列二次函数的图象与x轴有无交点,说明理由。
(1),
(2),
(3).
同学们先通过计算来说明,再找三名学生用几何画板绘制函数图象验证。
(二)引入新课:
(1)返回到第二张图:观察图象回答,抛物线被x轴分成了几部分?
(三部分:x轴上方,x轴下方,x轴上)
(2)老师引导,师生共同探究:
图象在x轴上,即,亦即.这时由图象得到自变量x的值是-1和3,是一元二次方程的解;
图象在x轴上方部分,即,也就是,这时由图象得自变量x的取值范围是或,是一元二次不等式的解集;
图象在x轴下方部分,即,也就是,这时由图象得自变量x的取值范围是,是一元二次不等式的解集。
(3)尝试用第三、四张图来解决下列问题:
①、的解集;
②的解,、的解集。
图四
图三
(三)课堂演练
(1)P34练习1求出一元二次方程的根,再结合二次函数的图象,求出当时,X的取值范围。
(先一起动手算出方程的根,再请一位同学绘制函数图图象,集体讨论后回答。)
(2)P34练习2结合函数的图象,求:
①
的解集;
②
的解集。
图五
图六
(四)课堂小结
这节课你们学到了什么?
教师鼓励学生积极回答,答不完整的没有关系,其它同学补充。以此培养学生的口头表达能力,归纳概括能力。并用多媒体把学生的归纳用一张表展示出来,告诉学生不必死记硬背,而是掌握其数形结合的基本原理和基本步骤。
一元二次不等式与一元二次方程及一元二次函数的关系
一元二次函数的图象
一元二次方程的根
有两实根
有两相等的实根
无实根
一元二次不等式的解集
全体实数
不等式的解集
无解
无解
解一元二次不等式的步骤:求根——画图——找解
(告诉学生,在非常熟悉的情况下可省略第二步,但应做到“成图在胸”)
(五)布置作业
P35
习题21.3第8、9两题。
