沪科版(2012)初中数学九上 21.4.1 实际问题与二次函数 同步练习(word版含答案)
文档属性
| 名称 | 沪科版(2012)初中数学九上 21.4.1 实际问题与二次函数 同步练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 77.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-15 16:04:35 | ||
图片预览

文档简介
《实际问题与二次函数》习题(三)
一、选择题
1.二次函数
y=
x
2+2
x-7的函数值是8,那么对应的
x的值是(???
)
A.3?
??
??
???B.5?
??
??
???C.-3和5?
??
??
?
D.3和-5
2.若二次函数
y=
x
2-
x与
y=-
x
2+
k的图象的顶点重合,则下列结论不正确的(???
)
A.这两个函数图象有相同的对称轴
B.这两个函数图象的开口方向相反
C.方程-
x
2+
k=0没有实数根
D.二次函数
y=-
x
2+
k的最大值为
k
3.抛物线
y=2
x
2+4
x-3的顶点坐标是(???
)??
A.(1,-5)
?
B.(-1,-5)
C.(-1,-4)?????
D.(-2,-7)
4.二次函数
y=ax
2+
bx+c的图像如图所示,
则点
A(
a,
b)在(???
)
A.
第一象限??
B.
第二象限??
C.
第三象限???
D.
第四象限
二、填空题
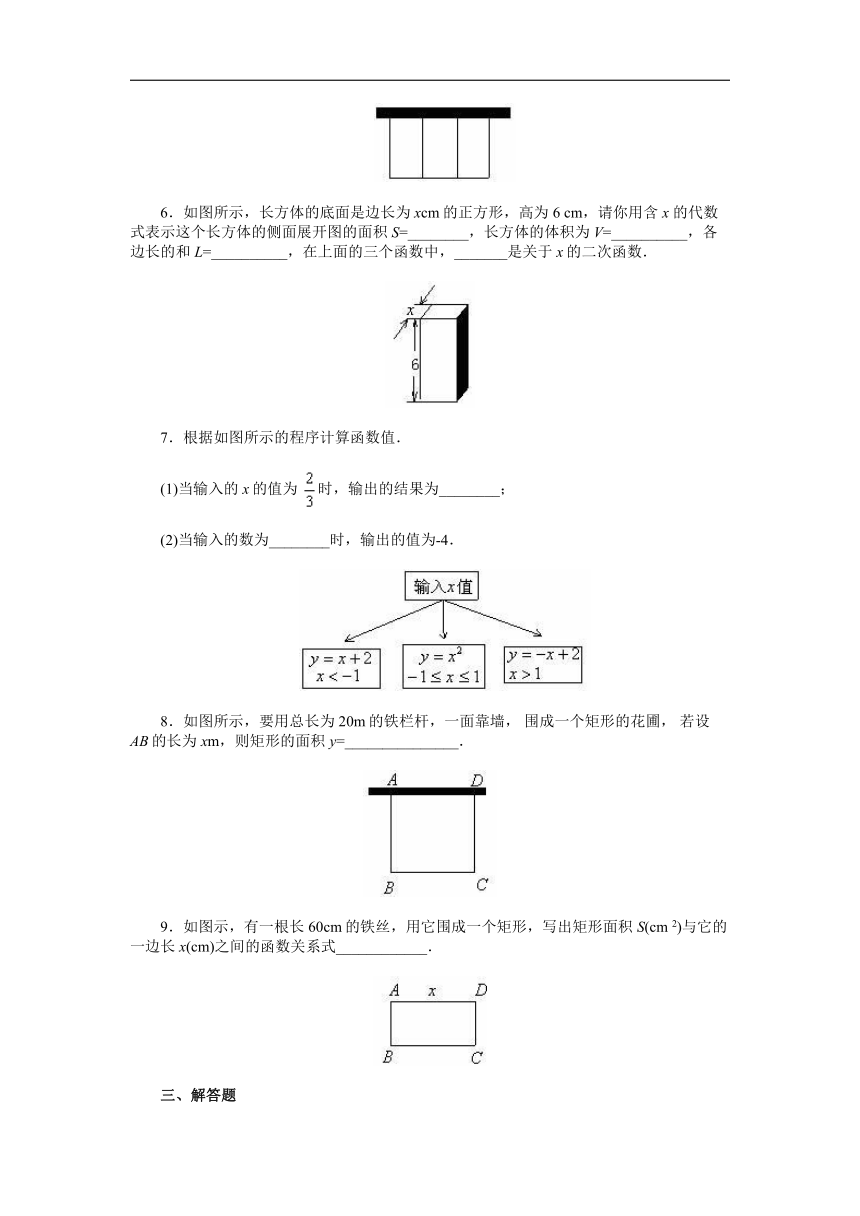
5.某学校依墙建羊圈,各面用木棍围成栅栏(如图),该校计划用木棍围出总长为24m的栅栏.设每间羊圈的长为
xm.
(1)请你用含
x的关系式来表示围成三间羊圈所利用的旧墙的总长度
L=_______,三间羊圈的总面积
S=____________;
(2)
S可以看成
x的_________,这里自变量
x的取值范围是_________;
(3)请计算,当羊圈的长分别为2m、3m、4m和5m时,羊圈的总面积分别为_____、_____、______、______,在这些数中,x取_____m时,面积
S最大.
6.如图所示,长方体的底面是边长为
xcm的正方形,高为6
cm,请你用含
x
的代数式表示这个长方体的侧面展开图的面积
S=________,长方体的体积为
V=__________,各边长的和
L=__________,在上面的三个函数中,_______是关于
x的二次函数.
7.根据如图所示的程序计算函数值.
(1)当输入的
x的值为
时,输出的结果为________;
(2)当输入的数为________时,输出的值为-4.
8.如图所示,要用总长为20m的铁栏杆,一面靠墙,
围成一个矩形的花圃,
若设
AB的长为
xm,则矩形的面积
y=_______________.
9.如图示,有一根长60cm的铁丝,用它围成一个矩形,写出矩形面积
S(cm
2)与它的一边长
x(cm)之间的函数关系式____________.
三、解答题
10.某商场以每件42元的价钱购进一种服装,根据试销得知:这种服装每天的销售量(件),与每件的销售价(元/件)可看成是一次函数关系:
(1)写出商场卖这种服装每天的销售利润与每件的销售价
之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);
(2)通过对所得函数关系式进行配方,指出:商场要想每天获得最大的销售利润,每件的销售价定为多少最为合适;最大销售利润为多少?
?
?
11.在体育测试时,初三的一名高个子男同学推铅球,已知铅球所经过的路线是某个二次函数图象的一部分,如图所示,如果这个男同学的出手处
A点的坐标(0,2),铅球路线的最高处
B点的坐标为(6,5)
(1)求这个二次函数的解析式;
(2)该男同学把铅球推出去多远?(精确到0.01米,
)
?
?
12.如图,有一块铁皮,拱形边缘呈抛物线状,
MN=4dm,抛物线顶点处到边
MN的距离是4dm,要在铁皮上截下一矩形
ABCD,使矩形顶点
B
、
C落在边
MN上,
A
、
D落在抛物线上,问这样截下去的矩形铁皮的周长能否等于8dm?
?
?
答案:
1.D?
2.A?
3.B
4.B
5.(1)-4
x+24;-4
x
2+24
x;
(2)二次函数;0<
x<6;
(3)32m
2;36m
2;32m
2;20m
2;3
6.24
x,6
x
2;8
x+24;
V=6
x
2?7
.(1)
(2)6或-6?
8.
y=-2
x
2+20
x(0<
x<10)
9.
S=-
x
2+30
x(0<
x<30)
10.(1)由题意,销售利润
y与每件的销售价
x之间的函数关系为:
?
y=(
x-42)(-3
x+204),即
y=-3
x
2+
330
x-8568.
(2)配方,得
y=-3(
x-55)
2+507.
∴当每件的销售价为55元时,可取得最大利润,每天最大销售利润为507元.
11.(1)
设二次函数的解析式为:
顶点坐标为
(6,5)
,设
?
A(0,2)在抛物线上
?
(2)
当时,
?
,
(不合题意,舍去)
(米)
答:该同学把铅球抛出13.75米.
12.分析?
由“抛物线”联想到二次函数.以
MN所在的直线为
x轴,点
M为原点建立直角坐标系.设抛物线的顶点为
P,则
M(0,0),
N(4,0),
P(2,4).用待定系数法求得抛物线的解析式为
.
设
A点坐标为(
x,
y),则
AD=BC=2
x-4,
AB=CD=y.
于是
.
且
x的取值范围是0<
x<4(
x≠2).
若
l=8,则
,即
.解得
.
而0<
x<4(
x≠2).故
l的值不可能取8,即截下的矩形周长不可能等于8dm.
注:本题还可在其他位置建立直角坐标系.
一、选择题
1.二次函数
y=
x
2+2
x-7的函数值是8,那么对应的
x的值是(???
)
A.3?
??
??
???B.5?
??
??
???C.-3和5?
??
??
?
D.3和-5
2.若二次函数
y=
x
2-
x与
y=-
x
2+
k的图象的顶点重合,则下列结论不正确的(???
)
A.这两个函数图象有相同的对称轴
B.这两个函数图象的开口方向相反
C.方程-
x
2+
k=0没有实数根
D.二次函数
y=-
x
2+
k的最大值为
k
3.抛物线
y=2
x
2+4
x-3的顶点坐标是(???
)??
A.(1,-5)
?
B.(-1,-5)
C.(-1,-4)?????
D.(-2,-7)
4.二次函数
y=ax
2+
bx+c的图像如图所示,
则点
A(
a,
b)在(???
)
A.
第一象限??
B.
第二象限??
C.
第三象限???
D.
第四象限
二、填空题
5.某学校依墙建羊圈,各面用木棍围成栅栏(如图),该校计划用木棍围出总长为24m的栅栏.设每间羊圈的长为
xm.
(1)请你用含
x的关系式来表示围成三间羊圈所利用的旧墙的总长度
L=_______,三间羊圈的总面积
S=____________;
(2)
S可以看成
x的_________,这里自变量
x的取值范围是_________;
(3)请计算,当羊圈的长分别为2m、3m、4m和5m时,羊圈的总面积分别为_____、_____、______、______,在这些数中,x取_____m时,面积
S最大.
6.如图所示,长方体的底面是边长为
xcm的正方形,高为6
cm,请你用含
x
的代数式表示这个长方体的侧面展开图的面积
S=________,长方体的体积为
V=__________,各边长的和
L=__________,在上面的三个函数中,_______是关于
x的二次函数.
7.根据如图所示的程序计算函数值.
(1)当输入的
x的值为
时,输出的结果为________;
(2)当输入的数为________时,输出的值为-4.
8.如图所示,要用总长为20m的铁栏杆,一面靠墙,
围成一个矩形的花圃,
若设
AB的长为
xm,则矩形的面积
y=_______________.
9.如图示,有一根长60cm的铁丝,用它围成一个矩形,写出矩形面积
S(cm
2)与它的一边长
x(cm)之间的函数关系式____________.
三、解答题
10.某商场以每件42元的价钱购进一种服装,根据试销得知:这种服装每天的销售量(件),与每件的销售价(元/件)可看成是一次函数关系:
(1)写出商场卖这种服装每天的销售利润与每件的销售价
之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);
(2)通过对所得函数关系式进行配方,指出:商场要想每天获得最大的销售利润,每件的销售价定为多少最为合适;最大销售利润为多少?
?
?
11.在体育测试时,初三的一名高个子男同学推铅球,已知铅球所经过的路线是某个二次函数图象的一部分,如图所示,如果这个男同学的出手处
A点的坐标(0,2),铅球路线的最高处
B点的坐标为(6,5)
(1)求这个二次函数的解析式;
(2)该男同学把铅球推出去多远?(精确到0.01米,
)
?
?
12.如图,有一块铁皮,拱形边缘呈抛物线状,
MN=4dm,抛物线顶点处到边
MN的距离是4dm,要在铁皮上截下一矩形
ABCD,使矩形顶点
B
、
C落在边
MN上,
A
、
D落在抛物线上,问这样截下去的矩形铁皮的周长能否等于8dm?
?
?
答案:
1.D?
2.A?
3.B
4.B
5.(1)-4
x+24;-4
x
2+24
x;
(2)二次函数;0<
x<6;
(3)32m
2;36m
2;32m
2;20m
2;3
6.24
x,6
x
2;8
x+24;
V=6
x
2?7
.(1)
(2)6或-6?
8.
y=-2
x
2+20
x(0<
x<10)
9.
S=-
x
2+30
x(0<
x<30)
10.(1)由题意,销售利润
y与每件的销售价
x之间的函数关系为:
?
y=(
x-42)(-3
x+204),即
y=-3
x
2+
330
x-8568.
(2)配方,得
y=-3(
x-55)
2+507.
∴当每件的销售价为55元时,可取得最大利润,每天最大销售利润为507元.
11.(1)
设二次函数的解析式为:
顶点坐标为
(6,5)
,设
?
A(0,2)在抛物线上
?
(2)
当时,
?
,
(不合题意,舍去)
(米)
答:该同学把铅球抛出13.75米.
12.分析?
由“抛物线”联想到二次函数.以
MN所在的直线为
x轴,点
M为原点建立直角坐标系.设抛物线的顶点为
P,则
M(0,0),
N(4,0),
P(2,4).用待定系数法求得抛物线的解析式为
.
设
A点坐标为(
x,
y),则
AD=BC=2
x-4,
AB=CD=y.
于是
.
且
x的取值范围是0<
x<4(
x≠2).
若
l=8,则
,即
.解得
.
而0<
x<4(
x≠2).故
l的值不可能取8,即截下的矩形周长不可能等于8dm.
注:本题还可在其他位置建立直角坐标系.
