人教版七年级数学上册3.4 实际问题与一元一次方程(配套问题)课件(共21张PPT)
文档属性
| 名称 | 人教版七年级数学上册3.4 实际问题与一元一次方程(配套问题)课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-17 15:52:23 | ||
图片预览





文档简介
(共21张PPT)
3.4实际问题与一元一次方程
——配套问题
新人教版
七年级上册
什么是配套问题?
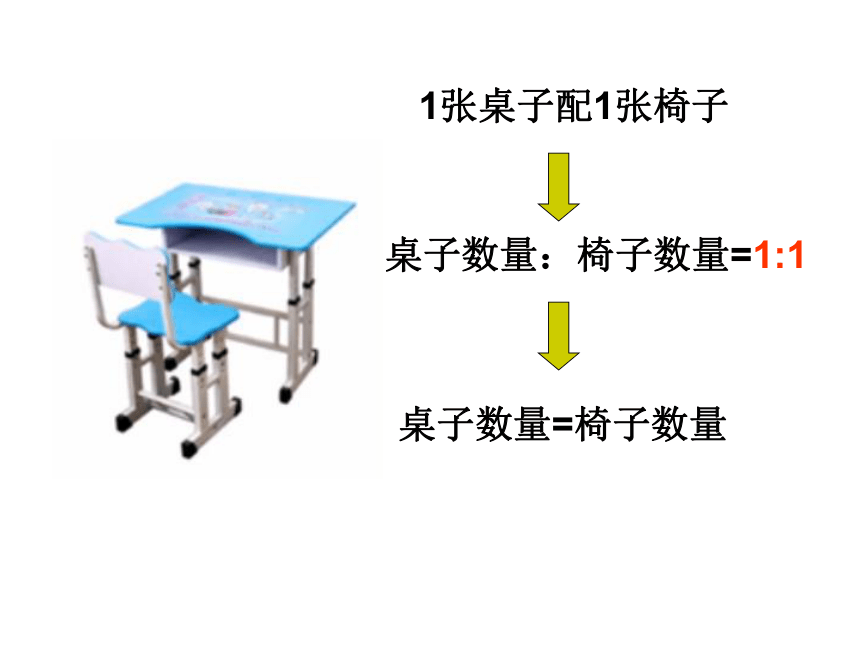
1张桌子配1张椅子
桌子数量:椅子数量=1:1
桌子数量=椅子数量
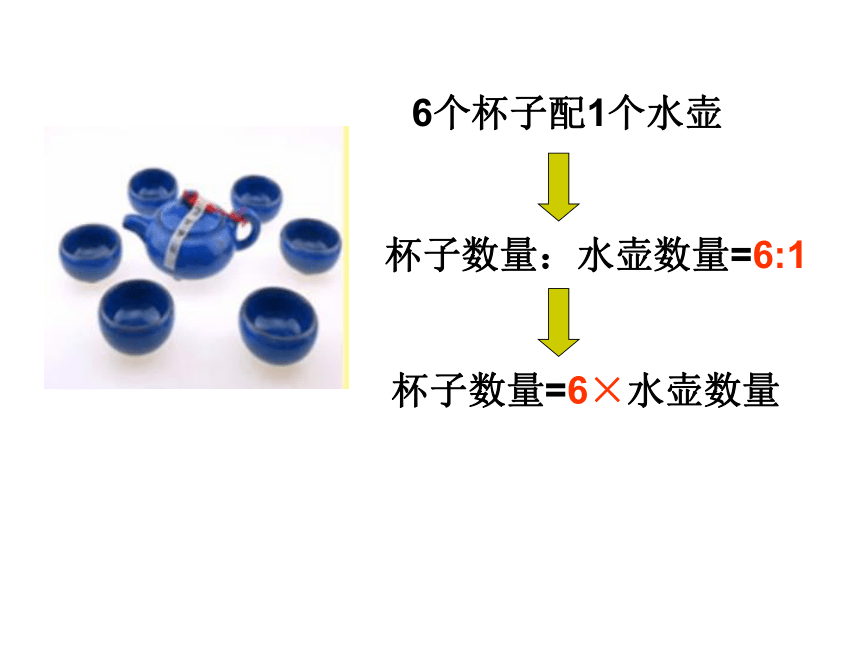
6个杯子配1个水壶
杯子数量:水壶数量=6:1
杯子数量=6×水壶数量
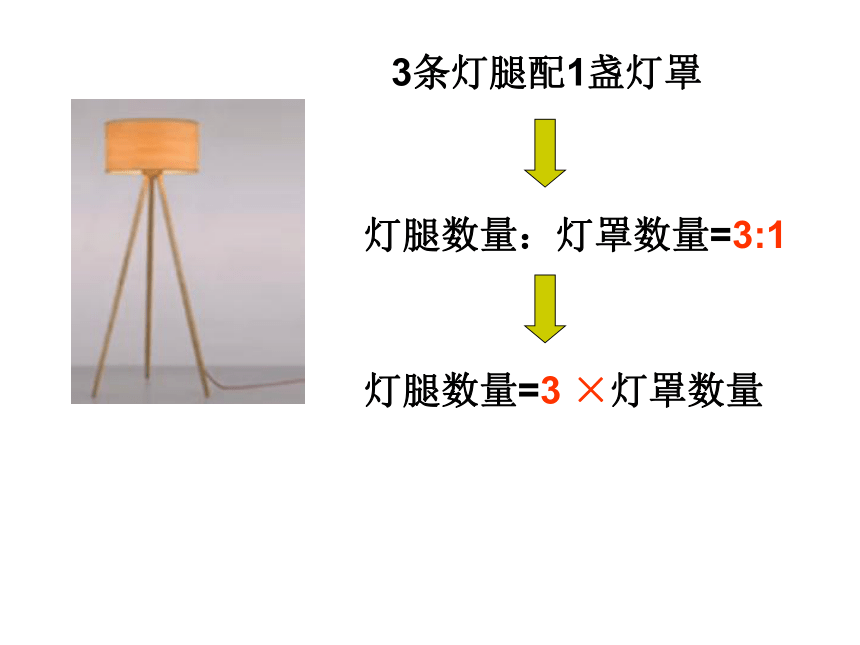
3条灯腿配1盏灯罩
灯腿数量:灯罩数量=3:1
灯腿数量=3
×灯罩数量
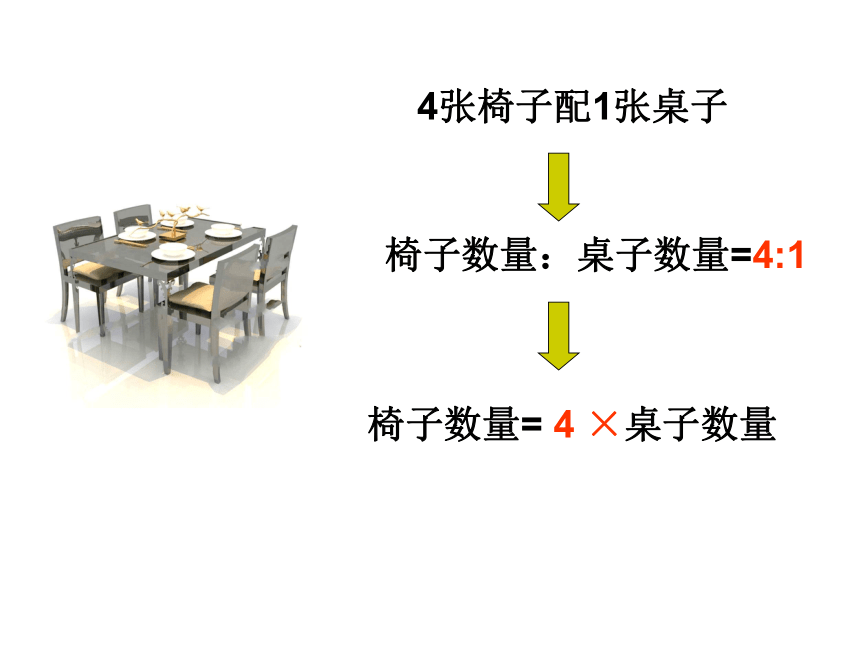
4张椅子配1张桌子
椅子数量:桌子数量=4:1
椅子数量=
4
×桌子数量
例
1
某车间22名工人生产螺钉和螺母,每人每天平均生产螺钉1200个或螺母2000个,一个螺钉要配两个螺母,为了使每天生产的产品刚好配套,应该分配多少名工人生产螺钉,多少工人生产螺母?
一、合作探究
列表分析:
产品类型
生产人数
单人产量
总产量
螺钉
x
1
200
螺母
2
000
×
=
1
200
x
×
=
2
000(22-x)
人数和为22人
(22﹣x)
螺母总产量是螺钉的2倍
2
000(22-x)
=
2×1
200x
二、探究新知
螺母的数量
=
2×螺钉的数量
解:设分配
x名工人生产螺钉,则生产螺母的人数
为(22-x)人.依题意,得:
去括号,得
44000
-
2000x
=
2400x
移项,得
-2000x
-
2400x
=
-44000
合并同类项,得
-4400x
=
-44000
系数化为1,得
x=10.
所以生产螺母的人数为:22-x=12(人).
答:分配10人生产螺钉,12人生产螺母.可使每天
生产的产品刚好配套。
2000(22-X)
=
2×1200X
互相交流:
1、此类配套问题一般有几个未知量要求?怎么设未知么设数?
2、配套问题的数量关系有何特点?
3、当问题中涉及到比较多量时应该怎么分析?
哪句话中隐含等量关系?怎么理解配套的意思?
哪句话中隐含等量关系?怎么理解配套的意思?
小结
解配套问题的方法规律:
A:B=x:y
yA=xB
找出有关配套的语句
X个A物体配y个B物体
⑴
一般有两个未知量需要求出来,
可先设其一为x,
再用含x的代数式表示另一个未知量。
⑵
往往其中一个量是另一个量的倍数或分数。
(3)此类涉及量多,常列出一个:
“三行四列”的表格来分析。
(三)收获新知:配套问题解法
1、课本
101页练习.一套仪器由一个A部件和三个B部件构成.
用1
m3钢材可以做40个A部件或240个B部件.
现要用6
m3钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
解:设应用
x
m3钢材做A部件,(6-x)
m3
钢材做B部件.
依题意得:
3×40
x=240
(6-x)
.
解方程,得:
x=4.
答:应用4
m3钢材做A部件,2
m3
钢材做B部件,配成这种仪器160套.
(四)、运用新知
2、课本106页习题3.4第2题变式题:一张方桌由一个桌面和四条桌腿组成,已知1
m3木料可制作桌面50张或桌腿300条,现在要用5
m3木料制作桌子,为使桌面与桌腿恰好配套,则用来制作桌腿的木料是多少立方米?
解:设桌面用木料x
m3,桌腿用木料(5-x)
m3.
依题意,得
50x×4=300(5-x).
解得x=3.
5-x=5-3=2.
答:用来制作桌腿的木料是2
m3.
(五)小结归纳
1、你能说说你在解决配套问题方面你获得了哪些经验?这些问题中的相等关系有什么特点?
2、甲、乙种零件,按m:n组装才配套,那么甲零件的数量与乙零件的数量有什么关系?
甲:乙=m:n
n×甲零件的数量
=
m×乙零件的数量
(六)抢答题,看看谁做得又对又快!
2.
某校社团活动课中,手工制作社的同学用一种彩色硬纸板制作某种长方体小礼品的包装盒,每张硬纸板可制作盒身12个,或制作盒底18个,1个盒身与2个盒底配成一套,现有42张这种彩色硬纸板,要使盒身和盒底刚好配套,若设需用x张做盒身,则下面所列方程正确的是(
)
A.18(42-x)=12x
B.2×18(42-x)=12x
C.18(42-x)=2×12x
D.18(21-x)=12x
C
3.有一张桌子配4张椅子,现有90立方米,1立方米可做木料可做5张椅子或1张桌子,要使桌子和椅子刚好配套,应该用x立方米的木料做桌子,则依题意可列方程为(
)
B.
C.
D.
A.
A
(七)作业设计,延续拓展
1、必做:教科书106页2、3小题
2、选做:结合身边的实例,自己编一道符合实际意义的应用题
3.4实际问题与一元一次方程
——配套问题
新人教版
七年级上册
什么是配套问题?
1张桌子配1张椅子
桌子数量:椅子数量=1:1
桌子数量=椅子数量
6个杯子配1个水壶
杯子数量:水壶数量=6:1
杯子数量=6×水壶数量
3条灯腿配1盏灯罩
灯腿数量:灯罩数量=3:1
灯腿数量=3
×灯罩数量
4张椅子配1张桌子
椅子数量:桌子数量=4:1
椅子数量=
4
×桌子数量
例
1
某车间22名工人生产螺钉和螺母,每人每天平均生产螺钉1200个或螺母2000个,一个螺钉要配两个螺母,为了使每天生产的产品刚好配套,应该分配多少名工人生产螺钉,多少工人生产螺母?
一、合作探究
列表分析:
产品类型
生产人数
单人产量
总产量
螺钉
x
1
200
螺母
2
000
×
=
1
200
x
×
=
2
000(22-x)
人数和为22人
(22﹣x)
螺母总产量是螺钉的2倍
2
000(22-x)
=
2×1
200x
二、探究新知
螺母的数量
=
2×螺钉的数量
解:设分配
x名工人生产螺钉,则生产螺母的人数
为(22-x)人.依题意,得:
去括号,得
44000
-
2000x
=
2400x
移项,得
-2000x
-
2400x
=
-44000
合并同类项,得
-4400x
=
-44000
系数化为1,得
x=10.
所以生产螺母的人数为:22-x=12(人).
答:分配10人生产螺钉,12人生产螺母.可使每天
生产的产品刚好配套。
2000(22-X)
=
2×1200X
互相交流:
1、此类配套问题一般有几个未知量要求?怎么设未知么设数?
2、配套问题的数量关系有何特点?
3、当问题中涉及到比较多量时应该怎么分析?
哪句话中隐含等量关系?怎么理解配套的意思?
哪句话中隐含等量关系?怎么理解配套的意思?
小结
解配套问题的方法规律:
A:B=x:y
yA=xB
找出有关配套的语句
X个A物体配y个B物体
⑴
一般有两个未知量需要求出来,
可先设其一为x,
再用含x的代数式表示另一个未知量。
⑵
往往其中一个量是另一个量的倍数或分数。
(3)此类涉及量多,常列出一个:
“三行四列”的表格来分析。
(三)收获新知:配套问题解法
1、课本
101页练习.一套仪器由一个A部件和三个B部件构成.
用1
m3钢材可以做40个A部件或240个B部件.
现要用6
m3钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
解:设应用
x
m3钢材做A部件,(6-x)
m3
钢材做B部件.
依题意得:
3×40
x=240
(6-x)
.
解方程,得:
x=4.
答:应用4
m3钢材做A部件,2
m3
钢材做B部件,配成这种仪器160套.
(四)、运用新知
2、课本106页习题3.4第2题变式题:一张方桌由一个桌面和四条桌腿组成,已知1
m3木料可制作桌面50张或桌腿300条,现在要用5
m3木料制作桌子,为使桌面与桌腿恰好配套,则用来制作桌腿的木料是多少立方米?
解:设桌面用木料x
m3,桌腿用木料(5-x)
m3.
依题意,得
50x×4=300(5-x).
解得x=3.
5-x=5-3=2.
答:用来制作桌腿的木料是2
m3.
(五)小结归纳
1、你能说说你在解决配套问题方面你获得了哪些经验?这些问题中的相等关系有什么特点?
2、甲、乙种零件,按m:n组装才配套,那么甲零件的数量与乙零件的数量有什么关系?
甲:乙=m:n
n×甲零件的数量
=
m×乙零件的数量
(六)抢答题,看看谁做得又对又快!
2.
某校社团活动课中,手工制作社的同学用一种彩色硬纸板制作某种长方体小礼品的包装盒,每张硬纸板可制作盒身12个,或制作盒底18个,1个盒身与2个盒底配成一套,现有42张这种彩色硬纸板,要使盒身和盒底刚好配套,若设需用x张做盒身,则下面所列方程正确的是(
)
A.18(42-x)=12x
B.2×18(42-x)=12x
C.18(42-x)=2×12x
D.18(21-x)=12x
C
3.有一张桌子配4张椅子,现有90立方米,1立方米可做木料可做5张椅子或1张桌子,要使桌子和椅子刚好配套,应该用x立方米的木料做桌子,则依题意可列方程为(
)
B.
C.
D.
A.
A
(七)作业设计,延续拓展
1、必做:教科书106页2、3小题
2、选做:结合身边的实例,自己编一道符合实际意义的应用题
