人教版七年级上册3.4 实际问题与一元一次方程(2) ——球赛积分表问题课件(16张)
文档属性
| 名称 | 人教版七年级上册3.4 实际问题与一元一次方程(2) ——球赛积分表问题课件(16张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-17 18:27:58 | ||
图片预览



文档简介
(共16张PPT)
学习目标
1.会通过列方程解决
“球赛积分问题”;
2.掌握列方程解决实际问题的一般步骤;
3.理解销售问题中的有关概念及相关数量关系。
重点
建立模型解决实际问题的一般方法。
难点
列方程解决
“球赛积分问题”。
你喜欢看篮球比赛吗?你对篮球比赛中的积分规则有了解吗?
情景引入
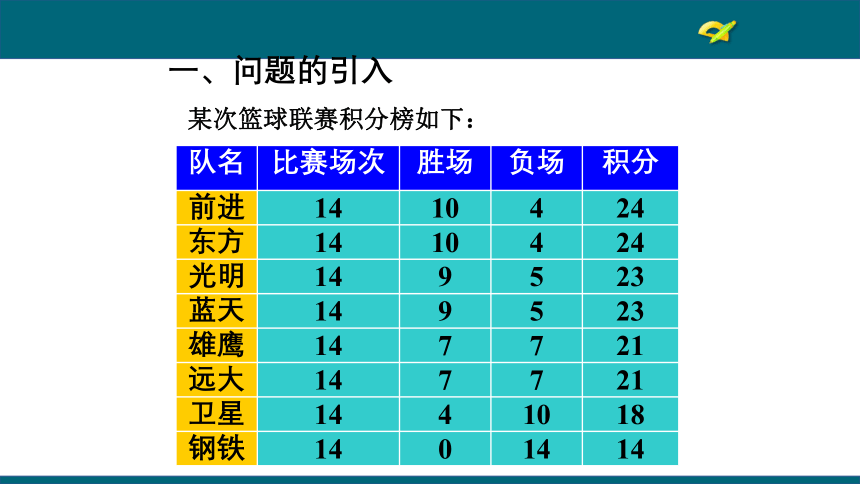
某次篮球联赛积分榜如下:
一、问题的引入
队名
比赛场次
胜场
负场
积分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
一、问题的引入
队名
比赛
场次
胜
场
负
场
积
分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
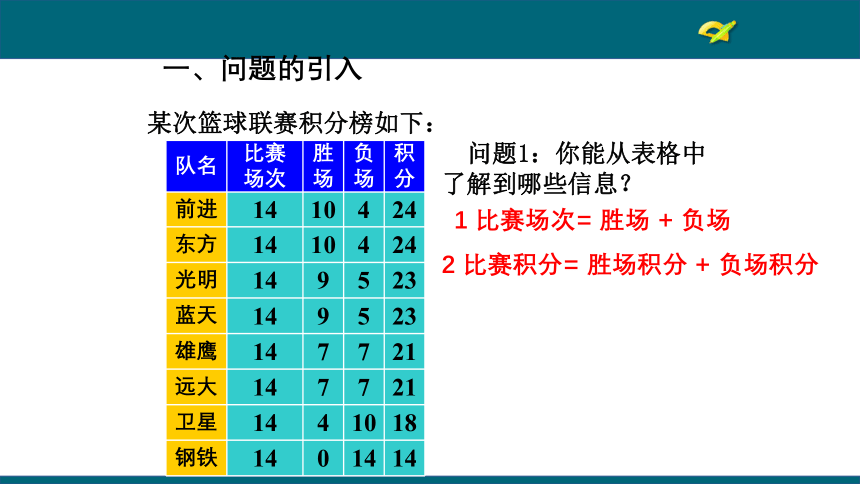
问题1:你能从表格中了解到哪些信息?
某次篮球联赛积分榜如下:
1
比赛场次=
胜场
+
负场
2
比赛积分=
胜场积分
+
负场积分
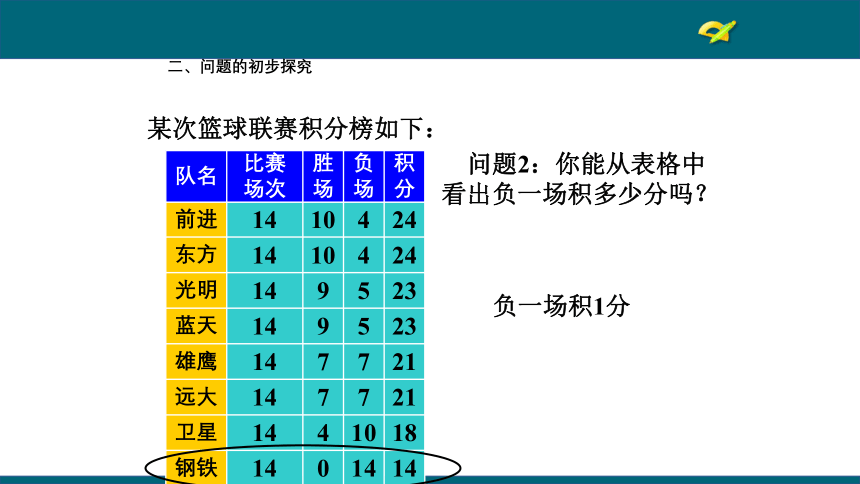
二、问题的初步探究
某次篮球联赛积分榜如下:
问题2:你能从表格中看出负一场积多少分吗?
队名
比赛
场次
胜
场
负
场
积
分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
负一场积1分
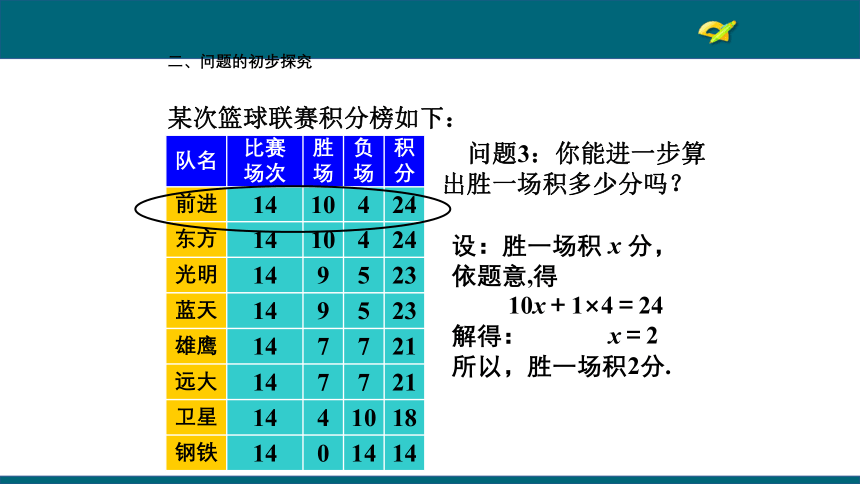
二、问题的初步探究
某次篮球联赛积分榜如下:
问题3:你能进一步算出胜一场积多少分吗?
队名
比赛
场次
胜
场
负
场
积
分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
设:胜一场积
x
分,
依题意,得
10x+1×4=24
解得:
x=2
所以,胜一场积2分.
某次篮球联赛积分榜如下:
队名
比赛场次
胜场
负场
积分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
问题4
怎样用式子表示总积分与胜、负场数之间的关系?
解:若一个队胜
m场,则负
(14-m)
场,胜场积分为
2m,负场积分为(14-m),
总积分为:
2m
+
(14-m)
=
m
+14.
即胜
m场的总积分为
(m
+14)
分.
问题5
某队胜场总积分能等于它负场总积分吗?
解:设一个队胜
x
场,则负
(14-x)
场,
依题意得
2x=14-x.
解得
x=
.
注意:解决实际问题时,要考虑得到的结果是不是符合实际.
x
表示什么量?它可以是分数吗?
x
表示所胜的场数,必须是整数,所以x=
不符合实际.
由此可以判定没有哪个队的胜场总积分等于负场总积分.
问题解决
例
某次篮球联赛共有十支队伍参赛,部分积分表如下:
队名
比赛场次
胜场
负场
积分
A
18
14
4
32
B
18
11
7
29
C
18
9
9
27
根据表格提供的信息,你能求出胜一场、负一场各积多少分吗?
【分析】关键信息是由C队的积分得出等量关系:胜场积分+负场积分=3.
典例解析
解:由C队的得分可知,胜场积分+负场积分=27÷9=3.设胜一场积x分,则负一场积(3-x)分.
根据A队得分,可列方程为
14x+4(3-x)=32,
解得x=2,则3-x=1.
答:胜一场积2分,则负一场积1分.
想一想:某队的胜场总积分能等于它的负场总积分吗?
能.
胜6场、负12场时,胜场总积分等于它的负场总积分.
典例解析
练一练(球赛积分问题)
某校组织院系足球赛,A队在第一轮比赛中共赛了11场,得分23分.比赛规定胜一场得3分,平一场得1分,负一场得0分,
A队在这一轮中只负了2场,那么这个队胜了几场?又平了几场呢?
解:设A队在第一轮比赛中共胜x场,则平了(11-2-x)场
3x
+(9-x)+
0×2
=
23
解得:x=7
则平了9-x=2场
答:这个队胜了7场,平了2场。
针对练习
回顾本课的学习过程,回答以下问题:
1.
你能读懂球赛积分表吗?
2.
如何通过积分表了解球赛的积分规则?
3.
借助方程解决实际问题,为什么要检验方程的解是否符合问题的实际意义?
五、课堂小结
如图是一张有4人参加的某项棋类循环比赛额定积分表,每场比赛胜者得3分,负者得-1分,和局两人各得1分。
(1)填出表内空格的分值;
(2)排除这次比赛的名次.
甲
乙
丙
丁
总分
甲
3
1
乙
-1
丙
1
3
丁
3
-1
-1
1
5
1
3
-3
3
7
-1
∴第一名:
丁
第二名:
甲
第三名:
丙
第四名:
乙
针对练习
2000赛季篮球甲A联赛部分球队积分榜:
(1)列式表示积分与胜、负场数之间的数量关系;
(2)某队的胜场总积分能等于它的负场总积分吗?
队名
比赛场次
胜场
负场
积分
八一双鹿
22
18
4
40
北京首钢
22
14
8
36
浙江万马
22
7
15
29
沈部雄狮
22
0
22
22
针对练习
下表中记录了一次试验中时间和温度的数据:
(1)如果温度的变化是均匀的,21分的温度是多少?
(2)什么时间的温度是34℃?
时间和温度的关系:
温度
T
随时间
t
增加而升高,每分钟温度升高3℃
73℃
T=10+3t
8分
学习目标
1.会通过列方程解决
“球赛积分问题”;
2.掌握列方程解决实际问题的一般步骤;
3.理解销售问题中的有关概念及相关数量关系。
重点
建立模型解决实际问题的一般方法。
难点
列方程解决
“球赛积分问题”。
你喜欢看篮球比赛吗?你对篮球比赛中的积分规则有了解吗?
情景引入
某次篮球联赛积分榜如下:
一、问题的引入
队名
比赛场次
胜场
负场
积分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
一、问题的引入
队名
比赛
场次
胜
场
负
场
积
分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
问题1:你能从表格中了解到哪些信息?
某次篮球联赛积分榜如下:
1
比赛场次=
胜场
+
负场
2
比赛积分=
胜场积分
+
负场积分
二、问题的初步探究
某次篮球联赛积分榜如下:
问题2:你能从表格中看出负一场积多少分吗?
队名
比赛
场次
胜
场
负
场
积
分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
负一场积1分
二、问题的初步探究
某次篮球联赛积分榜如下:
问题3:你能进一步算出胜一场积多少分吗?
队名
比赛
场次
胜
场
负
场
积
分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
设:胜一场积
x
分,
依题意,得
10x+1×4=24
解得:
x=2
所以,胜一场积2分.
某次篮球联赛积分榜如下:
队名
比赛场次
胜场
负场
积分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
问题4
怎样用式子表示总积分与胜、负场数之间的关系?
解:若一个队胜
m场,则负
(14-m)
场,胜场积分为
2m,负场积分为(14-m),
总积分为:
2m
+
(14-m)
=
m
+14.
即胜
m场的总积分为
(m
+14)
分.
问题5
某队胜场总积分能等于它负场总积分吗?
解:设一个队胜
x
场,则负
(14-x)
场,
依题意得
2x=14-x.
解得
x=
.
注意:解决实际问题时,要考虑得到的结果是不是符合实际.
x
表示什么量?它可以是分数吗?
x
表示所胜的场数,必须是整数,所以x=
不符合实际.
由此可以判定没有哪个队的胜场总积分等于负场总积分.
问题解决
例
某次篮球联赛共有十支队伍参赛,部分积分表如下:
队名
比赛场次
胜场
负场
积分
A
18
14
4
32
B
18
11
7
29
C
18
9
9
27
根据表格提供的信息,你能求出胜一场、负一场各积多少分吗?
【分析】关键信息是由C队的积分得出等量关系:胜场积分+负场积分=3.
典例解析
解:由C队的得分可知,胜场积分+负场积分=27÷9=3.设胜一场积x分,则负一场积(3-x)分.
根据A队得分,可列方程为
14x+4(3-x)=32,
解得x=2,则3-x=1.
答:胜一场积2分,则负一场积1分.
想一想:某队的胜场总积分能等于它的负场总积分吗?
能.
胜6场、负12场时,胜场总积分等于它的负场总积分.
典例解析
练一练(球赛积分问题)
某校组织院系足球赛,A队在第一轮比赛中共赛了11场,得分23分.比赛规定胜一场得3分,平一场得1分,负一场得0分,
A队在这一轮中只负了2场,那么这个队胜了几场?又平了几场呢?
解:设A队在第一轮比赛中共胜x场,则平了(11-2-x)场
3x
+(9-x)+
0×2
=
23
解得:x=7
则平了9-x=2场
答:这个队胜了7场,平了2场。
针对练习
回顾本课的学习过程,回答以下问题:
1.
你能读懂球赛积分表吗?
2.
如何通过积分表了解球赛的积分规则?
3.
借助方程解决实际问题,为什么要检验方程的解是否符合问题的实际意义?
五、课堂小结
如图是一张有4人参加的某项棋类循环比赛额定积分表,每场比赛胜者得3分,负者得-1分,和局两人各得1分。
(1)填出表内空格的分值;
(2)排除这次比赛的名次.
甲
乙
丙
丁
总分
甲
3
1
乙
-1
丙
1
3
丁
3
-1
-1
1
5
1
3
-3
3
7
-1
∴第一名:
丁
第二名:
甲
第三名:
丙
第四名:
乙
针对练习
2000赛季篮球甲A联赛部分球队积分榜:
(1)列式表示积分与胜、负场数之间的数量关系;
(2)某队的胜场总积分能等于它的负场总积分吗?
队名
比赛场次
胜场
负场
积分
八一双鹿
22
18
4
40
北京首钢
22
14
8
36
浙江万马
22
7
15
29
沈部雄狮
22
0
22
22
针对练习
下表中记录了一次试验中时间和温度的数据:
(1)如果温度的变化是均匀的,21分的温度是多少?
(2)什么时间的温度是34℃?
时间和温度的关系:
温度
T
随时间
t
增加而升高,每分钟温度升高3℃
73℃
T=10+3t
8分
