人教版七年级上册4.2 直线、射线、线段(2) 课件(22张)
文档属性
| 名称 | 人教版七年级上册4.2 直线、射线、线段(2) 课件(22张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-17 18:25:30 | ||
图片预览




文档简介
(共22张PPT)
义务教育教科书
数学
七年级
上册
4.2.1
直线、射线、线段(2)
类型
线段
射线
直线
端点
有2个端点
延伸方向
可不可度量
可度量
有1个端点
向一个方向无限延伸
不可度量
无端点
向两个方向无限延伸
不可度量
不向任何一方延伸
说一说:联系和区别
线段和射线都是直线的一部分.
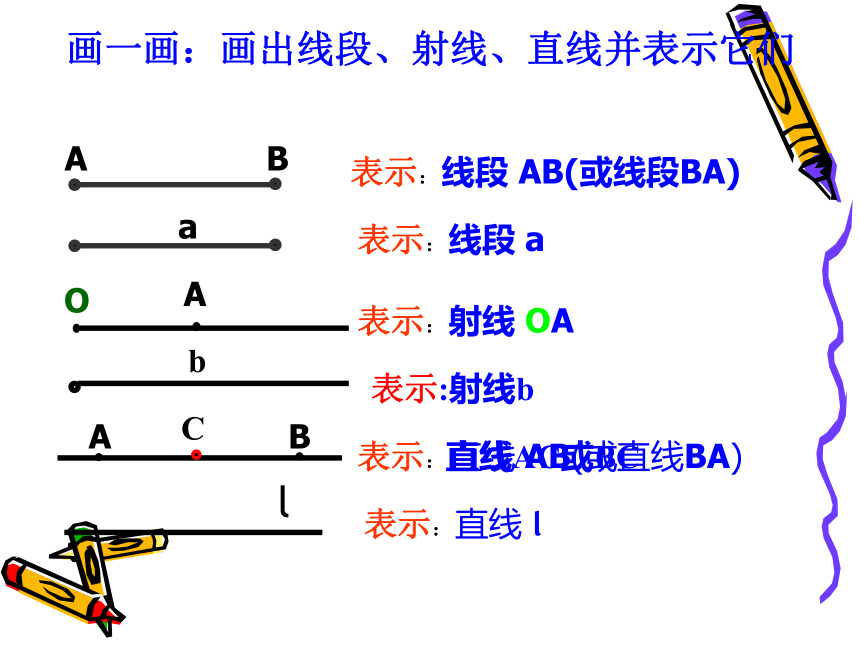
画一画:画出线段、射线、直线并表示它们
O
A
B
表示:线段
AB(或线段BA)
a
表示:线段
a
A
表示:射线
OA
A
B
表示:直线
AB(或直线BA)
l
表示:直线
l
表示:射线b
b
C
直线AC或BC
学习目标:
1、会画线段,并比较线段的长短;
2、了解线段的和,差,中点的含义;
3、理解线段的性质和距离的定义。
教学重点和难点:
1、了解中点的含义和线段的性质;
2、会画线段,并比较线段的长短。
姚
明身高:2.26米
易建联身高:2.13米
你知道他们谁更高吗?
你是怎样得出这个结论的呢?
那你知道如何比较两条线段的长短吗?
目测法
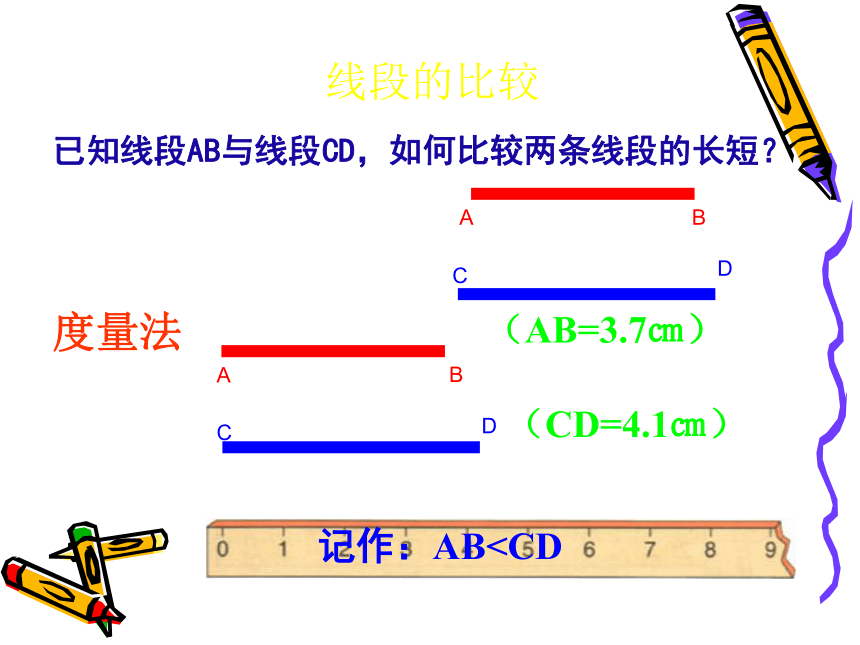
已知线段AB与线段CD,如何比较两条线段的长短?
A
B
D
C
线段的比较
度量法
A
B
(AB=3.7㎝)
(CD=4.1㎝)
记作:ABD
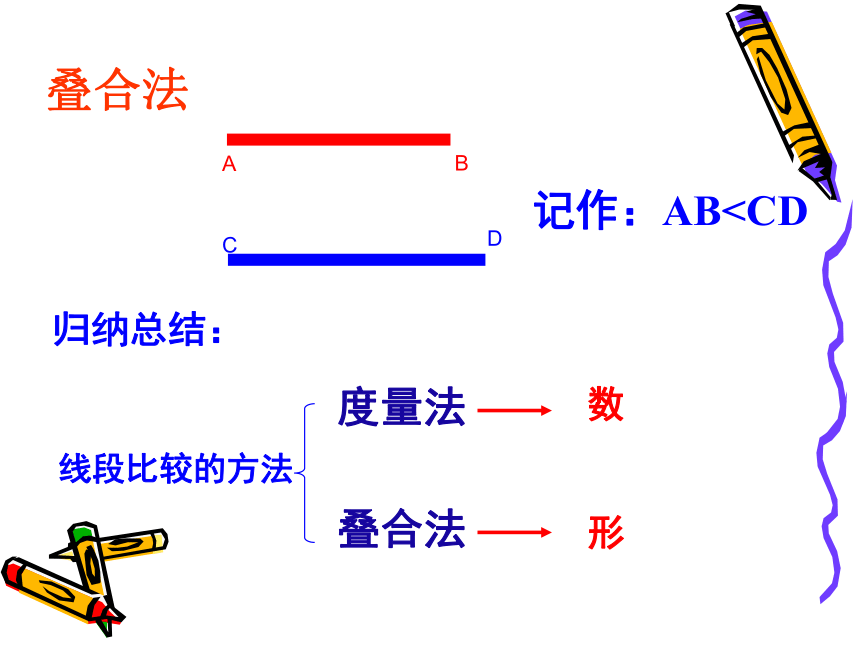
C
记作:ABA
B
D
C
叠合法
归纳总结:
线段比较的方法
度量法
数
叠合法
形
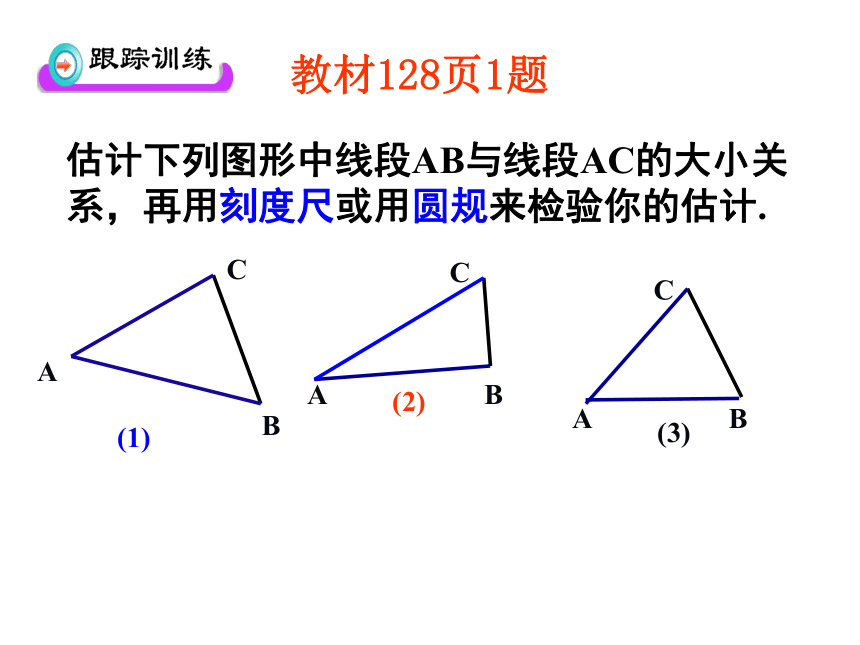
教材128页1题
估计下列图形中线段AB与线段AC的大小关系,再用刻度尺或用圆规来检验你的估计.
(1)
A
B
C
A
(2)
B
C
A
(3)
B
C
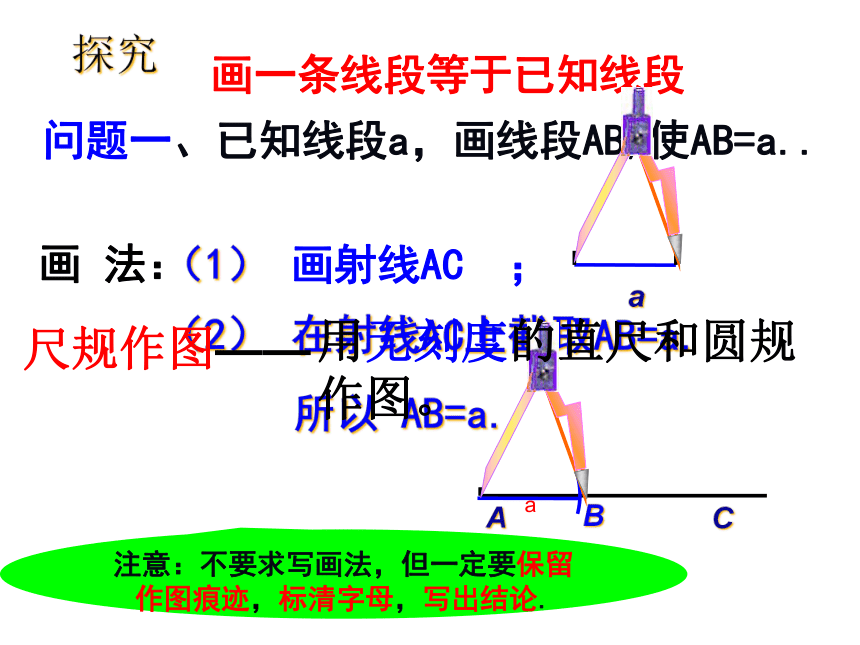
注意:不要求写画法,但一定要保留作图痕迹,标清字母,写出结论.
a
(1)
画射线AC
;
A
C
(2)
在射线AC上截取AB=a.
B
所以
AB=a.
画
法:
问题一、已知线段a,画线段AB,使AB=a..
画一条线段等于已知线段
探究
a
尺规作图——
用无刻度的直尺和圆规
作图。
A
①先画一条直线l;
②在直线
l上依次截取
AC
=
a
,CB=b。
问题二:已知线段a、b,画一条线段AB,
使AB=a+b.
b
C
a
b
B
所以AB=a+b.
画法:
l
a
画一条线段等于已知线段的和
A
l
①先用直尺画一条直线l;
②在直线l上截取AD
=
b;
问题三:已知线段a,b(b>a)画一条线段AC,使AC=b-a。
a
b
C
b
D
所以AC=b-a。
画法:
a
在线段AD上截取DC=a。
画一条线段等于已知线段的差
已知线段a、b,画线段AB,使AB=2a-b.
a
b
A
l
C
a
D
a
b
B
解:
(2)在直线l上顺序截取
AC=a,CD=a.
(3)在线段AD上截取BD=b.
线段AB=2a-b.
(1)画一条直线l.
课本128页练习2题
归纳总结:
1.线段比较的方法
度量法
数
叠合法
形
注意:不要求大家写画法,但是一定要保留作图痕迹,标清字母,写出结论.
要一量,二算,三画.
2线段的画法
截取法
度量法
你能用这根绳子正好做一双鞋带吗?
情景探究2:
线段的分点及和,差
A
B
M
点M把线段AB分成相等的两条线段AM与MB,我们把M点叫做线段AB的中点.
看一看说一说
如果我们把拉直的线绳看作线段AB,刚才的折点看作点M,观察线段AM与BM的关系.
文字叙述:
数学符号语言:
因为点M是线段AB的中点
所以AM=MB=
AB,AB=2AM=2BM
AM=MB
A
B
M
N
A
B
M
M、N为线段AB的三等分点
AM=MN=NB=
AB;
AB=3AM=3MN=3NB
N
P
M、N、P为线段AB的四等分点
AN=MN=MP=PB=
AB;
AB=4AN=4MN=4NP=4PB
根据图形填空:
(1)AC=
_____
+
______
A
B
C
(2)(如图)增加一个D点,则,
AC=
_____+
_____+
_____
D
思维测评
AB
BC
AB
BD
DC
1、如图,AB=CD,
则AC与BD的大小关系是(
).
A.
AC>BD
B.
ACC.AC=BD
D.
不能确定
2、如图,已知AB=6cm,AD=4cm,BC=5cm,则CD=
。
3、点M是线段AB的中点,AM=8cm,则
BM=
,
AB=
.
考考你的眼力!
C
9
4
8
4、已知线段AB=12cm,点M是它的一个
三等分点,
则AM=___________cm.
再接再厉
5、如果点B在线段AC上,那么下列表达
式能表示B是线段AB中点的有
个。
(1)AC=BC
(2)AC=2AB
(3)
AB=0.5AC
(4)AB+BC=AC
4或8
2
拓展学识
A
B
如图,从A地到B地有四条道路,除它们之外能否再修一条从A地到B地的最短道路?如果能,请联系你以前所学的知识,在图上画出最短路线.
1.
两点的所有连线中,线段最短.
简单地说:两点之间,线段最短.
2.
连接两点间的线段的长度,叫做这两点的距离.
课后作业
1、P128
练习第2、3题;
2、P130
习题第9、10题;
3、同步训练P~80。
你是雄鹰就要展翅翱翔!
同学们
再见
义务教育教科书
数学
七年级
上册
4.2.1
直线、射线、线段(2)
类型
线段
射线
直线
端点
有2个端点
延伸方向
可不可度量
可度量
有1个端点
向一个方向无限延伸
不可度量
无端点
向两个方向无限延伸
不可度量
不向任何一方延伸
说一说:联系和区别
线段和射线都是直线的一部分.
画一画:画出线段、射线、直线并表示它们
O
A
B
表示:线段
AB(或线段BA)
a
表示:线段
a
A
表示:射线
OA
A
B
表示:直线
AB(或直线BA)
l
表示:直线
l
表示:射线b
b
C
直线AC或BC
学习目标:
1、会画线段,并比较线段的长短;
2、了解线段的和,差,中点的含义;
3、理解线段的性质和距离的定义。
教学重点和难点:
1、了解中点的含义和线段的性质;
2、会画线段,并比较线段的长短。
姚
明身高:2.26米
易建联身高:2.13米
你知道他们谁更高吗?
你是怎样得出这个结论的呢?
那你知道如何比较两条线段的长短吗?
目测法
已知线段AB与线段CD,如何比较两条线段的长短?
A
B
D
C
线段的比较
度量法
A
B
(AB=3.7㎝)
(CD=4.1㎝)
记作:AB
C
记作:AB
B
D
C
叠合法
归纳总结:
线段比较的方法
度量法
数
叠合法
形
教材128页1题
估计下列图形中线段AB与线段AC的大小关系,再用刻度尺或用圆规来检验你的估计.
(1)
A
B
C
A
(2)
B
C
A
(3)
B
C
注意:不要求写画法,但一定要保留作图痕迹,标清字母,写出结论.
a
(1)
画射线AC
;
A
C
(2)
在射线AC上截取AB=a.
B
所以
AB=a.
画
法:
问题一、已知线段a,画线段AB,使AB=a..
画一条线段等于已知线段
探究
a
尺规作图——
用无刻度的直尺和圆规
作图。
A
①先画一条直线l;
②在直线
l上依次截取
AC
=
a
,CB=b。
问题二:已知线段a、b,画一条线段AB,
使AB=a+b.
b
C
a
b
B
所以AB=a+b.
画法:
l
a
画一条线段等于已知线段的和
A
l
①先用直尺画一条直线l;
②在直线l上截取AD
=
b;
问题三:已知线段a,b(b>a)画一条线段AC,使AC=b-a。
a
b
C
b
D
所以AC=b-a。
画法:
a
在线段AD上截取DC=a。
画一条线段等于已知线段的差
已知线段a、b,画线段AB,使AB=2a-b.
a
b
A
l
C
a
D
a
b
B
解:
(2)在直线l上顺序截取
AC=a,CD=a.
(3)在线段AD上截取BD=b.
线段AB=2a-b.
(1)画一条直线l.
课本128页练习2题
归纳总结:
1.线段比较的方法
度量法
数
叠合法
形
注意:不要求大家写画法,但是一定要保留作图痕迹,标清字母,写出结论.
要一量,二算,三画.
2线段的画法
截取法
度量法
你能用这根绳子正好做一双鞋带吗?
情景探究2:
线段的分点及和,差
A
B
M
点M把线段AB分成相等的两条线段AM与MB,我们把M点叫做线段AB的中点.
看一看说一说
如果我们把拉直的线绳看作线段AB,刚才的折点看作点M,观察线段AM与BM的关系.
文字叙述:
数学符号语言:
因为点M是线段AB的中点
所以AM=MB=
AB,AB=2AM=2BM
AM=MB
A
B
M
N
A
B
M
M、N为线段AB的三等分点
AM=MN=NB=
AB;
AB=3AM=3MN=3NB
N
P
M、N、P为线段AB的四等分点
AN=MN=MP=PB=
AB;
AB=4AN=4MN=4NP=4PB
根据图形填空:
(1)AC=
_____
+
______
A
B
C
(2)(如图)增加一个D点,则,
AC=
_____+
_____+
_____
D
思维测评
AB
BC
AB
BD
DC
1、如图,AB=CD,
则AC与BD的大小关系是(
).
A.
AC>BD
B.
AC
D.
不能确定
2、如图,已知AB=6cm,AD=4cm,BC=5cm,则CD=
。
3、点M是线段AB的中点,AM=8cm,则
BM=
,
AB=
.
考考你的眼力!
C
9
4
8
4、已知线段AB=12cm,点M是它的一个
三等分点,
则AM=___________cm.
再接再厉
5、如果点B在线段AC上,那么下列表达
式能表示B是线段AB中点的有
个。
(1)AC=BC
(2)AC=2AB
(3)
AB=0.5AC
(4)AB+BC=AC
4或8
2
拓展学识
A
B
如图,从A地到B地有四条道路,除它们之外能否再修一条从A地到B地的最短道路?如果能,请联系你以前所学的知识,在图上画出最短路线.
1.
两点的所有连线中,线段最短.
简单地说:两点之间,线段最短.
2.
连接两点间的线段的长度,叫做这两点的距离.
课后作业
1、P128
练习第2、3题;
2、P130
习题第9、10题;
3、同步训练P~80。
你是雄鹰就要展翅翱翔!
同学们
再见
