人教版 八年级数学上册 12.2 全等三角形的判定 同步训练(Word版 含答案)
文档属性
| 名称 | 人教版 八年级数学上册 12.2 全等三角形的判定 同步训练(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 437.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-14 23:49:33 | ||
图片预览



文档简介
人教版 八年级数学上册 12.2 全等三角形的判定 同步训练
一、选择题
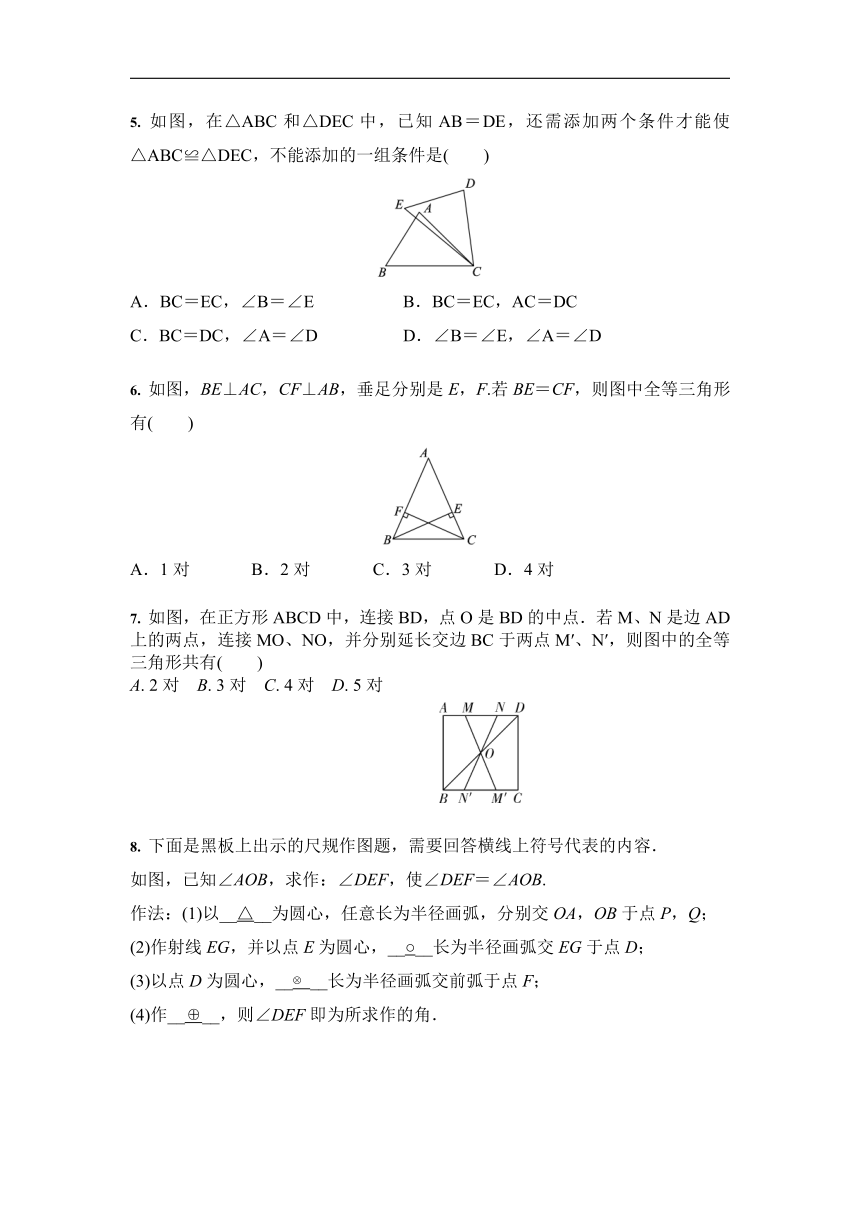
1. 下列三角形中全等的是( )
A.①② B.②③ C.③④ D.①④
2. 如图,要用“SAS”证明△ABC≌△ADE,若已知AB=AD,AC=AE,则还需添加条件( )
A.∠B=∠D B.∠C=∠E
C.∠1=∠2 D.∠3=∠4
3. 如图,AB=DE,AC=DF,BC=EF,则∠D的度数为( )
A.30° B.50° C.60° D.100°
4. 如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF的是( )
A.∠A=∠D B.BC=EF
C.∠ACB=∠F D.AC=DF
5. 如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
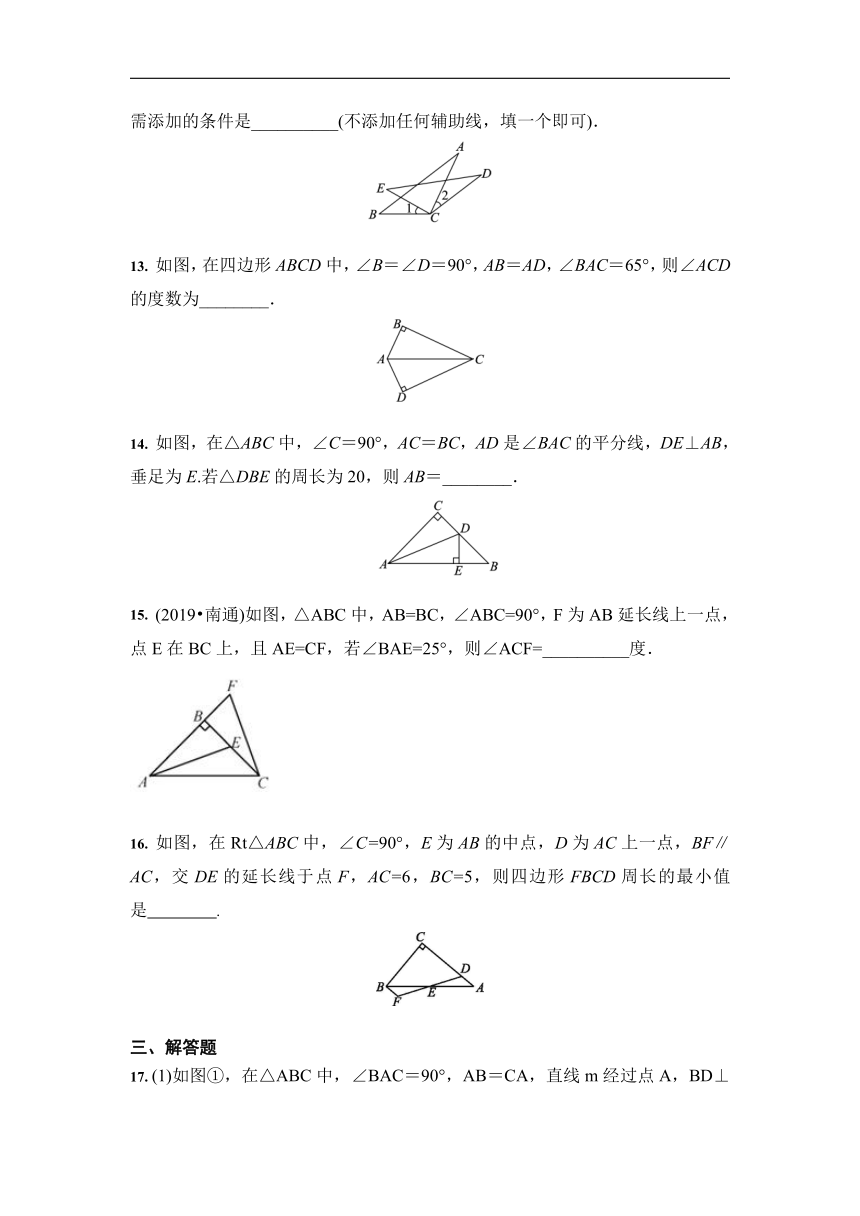
6. 如图,BE⊥AC,CF⊥AB,垂足分别是E,F.若BE=CF,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
7. 如图,在正方形ABCD中,连接BD,点O是BD的中点.若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
A. 2对 B. 3对 C. 4对 D. 5对
8. 下面是黑板上出示的尺规作图题,需要回答横线上符号代表的内容.
如图,已知∠AOB,求作:∠DEF,使∠DEF=∠AOB.
作法:(1)以__△__为圆心,任意长为半径画弧,分别交OA,OB于点P,Q;
(2)作射线EG,并以点E为圆心,__○__长为半径画弧交EG于点D;
(3)以点D为圆心,__?__长为半径画弧交前弧于点F;
(4)作__⊕__,则∠DEF即为所求作的角.
则下列回答正确的是( )
A.△表示点E B.○表示ED
C.?表示OP D.⊕表示射线EF
9. 如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到
玻璃店去配一块完全一样的玻璃,那么最省事的办法是带哪一块去 ( )
A. ① B. ②
C. ③ D. ①和②
10. 现已知线段a,b(a小惠:①以点O为圆心、线段a的长为半径画弧,交射线ON于点A;②以点A为圆心、线段b的长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
小雷:①以点O为圆心、线段a的长为半径画弧,交射线ON于点A;②以点O为圆心、线段b的长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
则下列说法中正确的是 ( )
A.小惠的作法正确,小雷的作法错误
B.小雷的作法正确,小惠的作法错误
C.两人的作法都正确
D.两人的作法都错误
二、填空题
11. 如图,已知AB=BC,要使△ABD≌△CBD,还需要添加一个条件,你添加的条件是____________.(只需写一个,不添加辅助线)
12. 如图,AB=DE,∠1=∠2,添加一个适当的条件,使△ABC≌△DEC,则需添加的条件是__________(不添加任何辅助线,填一个即可).
13. 如图,在四边形ABCD中,∠B=∠D=90°,AB=AD,∠BAC=65°,则∠ACD的度数为________.
14. 如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.若△DBE的周长为20,则AB=________.
15. (2019?南通)如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF,若∠BAE=25°,则∠ACF=__________度.
16. 如图,在Rt△ABC中,∠C=90°,E为AB的中点,D为AC上一点,BF∥AC,交DE的延长线于点F,AC=6,BC=5,则四边形FBCD周长的最小值是 .
三、解答题
17. (1)如图①,在△ABC中,∠BAC=90°,AB=CA,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为D,E.求证:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=CA,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角,则结论DE=BD+CE是否成立?若成立,请你给出证明;若不成立,请说明理由.
18. 在四边形ABCD中,AB=AD.
(1)如图①,若∠B=∠D=90°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD.请直接写出线段EF,BE,FD之间的数量关系:____________.
(2)如图②,若∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)如图③,若∠B+∠ADC=180°,E,F分别是边BC,CD延长线上的点,且∠EAF=∠BAD,请直接写出EF,BE,FD三者的数量关系.
19. 如图,已知AD是△ABC的中线,AM⊥AB,AM=AB,AN⊥AC,AN=AC.
求证:MN=2AD.
人教版 八年级数学上册 12.2 全等三角形的判定 同步训练-答案
一、选择题
1. 【答案】A [解析] ①②符合证明三角形全等的判定方法“SAS”.③④中相等的角所对的边不相等,所以不可能全等.故选A.
2. 【答案】C [解析] 还需添加条件∠1=∠2.
理由:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE.
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS).
3. 【答案】D [解析] 在△ABC和△DEF中,
∴△ABC≌△DEF.∴∠A=∠D.
∵∠A=180°-∠B-∠C=100°,∴∠D=100°.
4. 【答案】D [解析] 已知∠B=∠DEF,AB=DE,
∴添加∠A=∠D,利用“ASA”可得△ABC≌△DEF;
添加BC=EF,利用“SAS”可得△ABC≌△DEF;
添加∠ACB=∠F,利用“AAS”可得△ABC≌△DEF;
添加AC=DF,不能证明△ABC≌△DEF.故选D.
5. 【答案】C
6. 【答案】C [解析] ①∵BE⊥AC,CF⊥AB,
∴∠CFB=∠BEC=90°.
在Rt△BCF和Rt△CBE中,
∴Rt△BCF≌Rt△CBE(HL).
②∵BE⊥AC,CF⊥AB,∴∠AFC=∠AEB=90°.在△ABE和△ACF中,
∴△ABE≌△ACF(AAS).
③设BE与CF相交于点O.
∵BE⊥AC,CF⊥AB,
∴∠OFB=∠OEC=90°.
∵△ABE≌△ACF,∴AB=AC,AE=AF.
∴BF=CE.
在△BOF和△COE中,
∴△BOF≌△COE(AAS).
7. 【答案】C 【解析】由题意可知,△ABD≌△CBD,△MON≌△M′ON′,△DON≌△BON′,△DOM≌△BOM′共4对.
8. 【答案】D
9. 【答案】 C
10. 【答案】A [解析] AB=b,AB是斜边,小惠作的斜边长是b符合条件,而小雷作的是一条直角边长是b.故小惠的作法正确,小雷的作法错误.
二、填空题
11. 【答案】答案不唯一,如AD=CD [解析] 因为AB=BC,BD=BD,所以:
(1)当AD=CD时,△ABD≌△CBD(SSS);
(2)当∠ABD=∠CBD时,△ABD≌△CBD(SAS);
(3)当∠A=∠C=90°时,Rt△ABD≌Rt△CBD(HL).
12. 【答案】答案不唯一,如∠B=∠E
13. 【答案】25°
14. 【答案】20 [解析] 由角平分线的性质可得CD=DE.易证Rt△ACD≌Rt△AED,则AC=AE,DE+DB=CD+DB=BC=AC=AE,故DE+DB+EB=AE+EB=AB.
15. 【答案】70
【解析】∵∠ABC=90°,AB=AC,∴∠CBF=180°–∠ABC=90°,∠ACB=45°,
在Rt△ABE和Rt△CBF中,,∴Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=25°,∴∠ACF=∠ACB+∠BCF=45°+25°=70°,故答案为:70.
16. 【答案】16 [解析] ∵BF∥AC,
∴∠EBF=∠EAD.
在△BFE和△ADE中,
∴△BFE≌△ADE(ASA).∴BF=AD.
∴BF+FD+CD+BC=AD+CD+FD+BC=AC+BC+FD=11+FD.
∵当FD⊥AC时,FD最短,此时FD=BC=5,
∴四边形FBCD周长的最小值为5+11=16.
三、解答题
17. 【答案】
解:(1)证明:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠AEC=90°.
∴∠BAD+∠ABD=90°.
∵∠BAC=90°,∴∠BAD+∠CAE=90°.
∴∠CAE=∠ABD.
在△ADB和△CEA中,
∴△ADB≌△CEA(AAS).
∴BD=AE,AD=CE.
∴DE=AE+AD=BD+CE.
(2)成立.
证明:∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠EAC=180°-α.
∴∠DBA=∠EAC.
在△ADB和△CEA中,
∴△ADB≌△CEA(AAS).
∴BD=AE,AD=CE.
∴DE=AE+AD=BD+CE.
18. 【答案】
解:(1)EF=BE+FD
(2)(1)中的结论EF=BE+FD仍然成立.
证明:如图,延长EB到点G,使BG=DF,连接AG.
∵∠ABC+∠D=180°,∠ABG+∠ABC=180°,∴∠ABG=∠D.
在△ABG与△ADF中,
∴△ABG≌△ADF(SAS).
∴AG=AF,∠1=∠2.
∴∠1+∠3=∠2+∠3=∠BAD-∠EAF.
又∵∠EAF=∠BAD,
∴∠1+∠3=∠BAD=∠EAF,
即∠EAG=∠EAF.
在△AEG和△AEF中,
∴△AEG≌△AEF.∴EG=EF.
∵EG=BE+BG,∴EF=BE+FD.
(3)EF=BE-FD.
19. 【答案】
证明:如图,延长AD至点E,使DE=AD,连接BE.
∵AD是△ABC的中线,
∴BD=CD.
在△BDE和△CDA中,
∴△BDE≌△CDA(SAS).
∴BE=AC=AN,∠DBE=∠DCA.
∴AC∥BE.∴∠ABE+∠BAC=180°.
∵∠BAM=∠CAN=90°,
∴∠MAN+∠BAC=180°.
∴∠ABE=∠MAN.
在△ABE和△MAN中,
∴△ABE≌△MAN(SAS).
∴AE=MN.
∵AE=2AD,∴MN=2AD.
一、选择题
1. 下列三角形中全等的是( )
A.①② B.②③ C.③④ D.①④
2. 如图,要用“SAS”证明△ABC≌△ADE,若已知AB=AD,AC=AE,则还需添加条件( )
A.∠B=∠D B.∠C=∠E
C.∠1=∠2 D.∠3=∠4
3. 如图,AB=DE,AC=DF,BC=EF,则∠D的度数为( )
A.30° B.50° C.60° D.100°
4. 如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF的是( )
A.∠A=∠D B.BC=EF
C.∠ACB=∠F D.AC=DF
5. 如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
6. 如图,BE⊥AC,CF⊥AB,垂足分别是E,F.若BE=CF,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
7. 如图,在正方形ABCD中,连接BD,点O是BD的中点.若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
A. 2对 B. 3对 C. 4对 D. 5对
8. 下面是黑板上出示的尺规作图题,需要回答横线上符号代表的内容.
如图,已知∠AOB,求作:∠DEF,使∠DEF=∠AOB.
作法:(1)以__△__为圆心,任意长为半径画弧,分别交OA,OB于点P,Q;
(2)作射线EG,并以点E为圆心,__○__长为半径画弧交EG于点D;
(3)以点D为圆心,__?__长为半径画弧交前弧于点F;
(4)作__⊕__,则∠DEF即为所求作的角.
则下列回答正确的是( )
A.△表示点E B.○表示ED
C.?表示OP D.⊕表示射线EF
9. 如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到
玻璃店去配一块完全一样的玻璃,那么最省事的办法是带哪一块去 ( )
A. ① B. ②
C. ③ D. ①和②
10. 现已知线段a,b(a
小雷:①以点O为圆心、线段a的长为半径画弧,交射线ON于点A;②以点O为圆心、线段b的长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
则下列说法中正确的是 ( )
A.小惠的作法正确,小雷的作法错误
B.小雷的作法正确,小惠的作法错误
C.两人的作法都正确
D.两人的作法都错误
二、填空题
11. 如图,已知AB=BC,要使△ABD≌△CBD,还需要添加一个条件,你添加的条件是____________.(只需写一个,不添加辅助线)
12. 如图,AB=DE,∠1=∠2,添加一个适当的条件,使△ABC≌△DEC,则需添加的条件是__________(不添加任何辅助线,填一个即可).
13. 如图,在四边形ABCD中,∠B=∠D=90°,AB=AD,∠BAC=65°,则∠ACD的度数为________.
14. 如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.若△DBE的周长为20,则AB=________.
15. (2019?南通)如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF,若∠BAE=25°,则∠ACF=__________度.
16. 如图,在Rt△ABC中,∠C=90°,E为AB的中点,D为AC上一点,BF∥AC,交DE的延长线于点F,AC=6,BC=5,则四边形FBCD周长的最小值是 .
三、解答题
17. (1)如图①,在△ABC中,∠BAC=90°,AB=CA,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为D,E.求证:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=CA,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角,则结论DE=BD+CE是否成立?若成立,请你给出证明;若不成立,请说明理由.
18. 在四边形ABCD中,AB=AD.
(1)如图①,若∠B=∠D=90°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD.请直接写出线段EF,BE,FD之间的数量关系:____________.
(2)如图②,若∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)如图③,若∠B+∠ADC=180°,E,F分别是边BC,CD延长线上的点,且∠EAF=∠BAD,请直接写出EF,BE,FD三者的数量关系.
19. 如图,已知AD是△ABC的中线,AM⊥AB,AM=AB,AN⊥AC,AN=AC.
求证:MN=2AD.
人教版 八年级数学上册 12.2 全等三角形的判定 同步训练-答案
一、选择题
1. 【答案】A [解析] ①②符合证明三角形全等的判定方法“SAS”.③④中相等的角所对的边不相等,所以不可能全等.故选A.
2. 【答案】C [解析] 还需添加条件∠1=∠2.
理由:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE.
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS).
3. 【答案】D [解析] 在△ABC和△DEF中,
∴△ABC≌△DEF.∴∠A=∠D.
∵∠A=180°-∠B-∠C=100°,∴∠D=100°.
4. 【答案】D [解析] 已知∠B=∠DEF,AB=DE,
∴添加∠A=∠D,利用“ASA”可得△ABC≌△DEF;
添加BC=EF,利用“SAS”可得△ABC≌△DEF;
添加∠ACB=∠F,利用“AAS”可得△ABC≌△DEF;
添加AC=DF,不能证明△ABC≌△DEF.故选D.
5. 【答案】C
6. 【答案】C [解析] ①∵BE⊥AC,CF⊥AB,
∴∠CFB=∠BEC=90°.
在Rt△BCF和Rt△CBE中,
∴Rt△BCF≌Rt△CBE(HL).
②∵BE⊥AC,CF⊥AB,∴∠AFC=∠AEB=90°.在△ABE和△ACF中,
∴△ABE≌△ACF(AAS).
③设BE与CF相交于点O.
∵BE⊥AC,CF⊥AB,
∴∠OFB=∠OEC=90°.
∵△ABE≌△ACF,∴AB=AC,AE=AF.
∴BF=CE.
在△BOF和△COE中,
∴△BOF≌△COE(AAS).
7. 【答案】C 【解析】由题意可知,△ABD≌△CBD,△MON≌△M′ON′,△DON≌△BON′,△DOM≌△BOM′共4对.
8. 【答案】D
9. 【答案】 C
10. 【答案】A [解析] AB=b,AB是斜边,小惠作的斜边长是b符合条件,而小雷作的是一条直角边长是b.故小惠的作法正确,小雷的作法错误.
二、填空题
11. 【答案】答案不唯一,如AD=CD [解析] 因为AB=BC,BD=BD,所以:
(1)当AD=CD时,△ABD≌△CBD(SSS);
(2)当∠ABD=∠CBD时,△ABD≌△CBD(SAS);
(3)当∠A=∠C=90°时,Rt△ABD≌Rt△CBD(HL).
12. 【答案】答案不唯一,如∠B=∠E
13. 【答案】25°
14. 【答案】20 [解析] 由角平分线的性质可得CD=DE.易证Rt△ACD≌Rt△AED,则AC=AE,DE+DB=CD+DB=BC=AC=AE,故DE+DB+EB=AE+EB=AB.
15. 【答案】70
【解析】∵∠ABC=90°,AB=AC,∴∠CBF=180°–∠ABC=90°,∠ACB=45°,
在Rt△ABE和Rt△CBF中,,∴Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=25°,∴∠ACF=∠ACB+∠BCF=45°+25°=70°,故答案为:70.
16. 【答案】16 [解析] ∵BF∥AC,
∴∠EBF=∠EAD.
在△BFE和△ADE中,
∴△BFE≌△ADE(ASA).∴BF=AD.
∴BF+FD+CD+BC=AD+CD+FD+BC=AC+BC+FD=11+FD.
∵当FD⊥AC时,FD最短,此时FD=BC=5,
∴四边形FBCD周长的最小值为5+11=16.
三、解答题
17. 【答案】
解:(1)证明:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠AEC=90°.
∴∠BAD+∠ABD=90°.
∵∠BAC=90°,∴∠BAD+∠CAE=90°.
∴∠CAE=∠ABD.
在△ADB和△CEA中,
∴△ADB≌△CEA(AAS).
∴BD=AE,AD=CE.
∴DE=AE+AD=BD+CE.
(2)成立.
证明:∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠EAC=180°-α.
∴∠DBA=∠EAC.
在△ADB和△CEA中,
∴△ADB≌△CEA(AAS).
∴BD=AE,AD=CE.
∴DE=AE+AD=BD+CE.
18. 【答案】
解:(1)EF=BE+FD
(2)(1)中的结论EF=BE+FD仍然成立.
证明:如图,延长EB到点G,使BG=DF,连接AG.
∵∠ABC+∠D=180°,∠ABG+∠ABC=180°,∴∠ABG=∠D.
在△ABG与△ADF中,
∴△ABG≌△ADF(SAS).
∴AG=AF,∠1=∠2.
∴∠1+∠3=∠2+∠3=∠BAD-∠EAF.
又∵∠EAF=∠BAD,
∴∠1+∠3=∠BAD=∠EAF,
即∠EAG=∠EAF.
在△AEG和△AEF中,
∴△AEG≌△AEF.∴EG=EF.
∵EG=BE+BG,∴EF=BE+FD.
(3)EF=BE-FD.
19. 【答案】
证明:如图,延长AD至点E,使DE=AD,连接BE.
∵AD是△ABC的中线,
∴BD=CD.
在△BDE和△CDA中,
∴△BDE≌△CDA(SAS).
∴BE=AC=AN,∠DBE=∠DCA.
∴AC∥BE.∴∠ABE+∠BAC=180°.
∵∠BAM=∠CAN=90°,
∴∠MAN+∠BAC=180°.
∴∠ABE=∠MAN.
在△ABE和△MAN中,
∴△ABE≌△MAN(SAS).
∴AE=MN.
∵AE=2AD,∴MN=2AD.
