人教版 八年级数学上册 13.1 轴对称 同步训练(Word版 含答案)
文档属性
| 名称 | 人教版 八年级数学上册 13.1 轴对称 同步训练(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 370.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-14 00:00:00 | ||
图片预览


文档简介
人教版 八年级数学上册 13.1 轴对称 同步训练
一、选择题
1. 点M(3,2)关于x轴对称的点的坐标为 ( )
A. (-3,2) B. (3,-2) C. (-3,-2) D. (3,2)
2. 如图,线段AB与A′B′(AB=A′B′)不关于直线l成轴对称的是( )
3. 如果点(m-1,-1)与点(5,-1)关于y轴对称,那么m的值为( )
A.4 B.-4 C.5 D.-5
4. 将一张长与宽的比为2∶1的长方形纸片按图①②所示的方式对折,然后沿图③中的虚线裁剪,得到图④,最后将图④中的纸片展开铺平,所得到的图案是( )
5. 在平面直角坐标系中,作点A(3,4)关于x轴的对称点A′,再将点A′向左平移6个单位长度,得到点B,则点B的坐标为( )
A.(4,-3) B.(-4,3)
C.(-3,4) D.(-3,-4)
6. [2018·河北] 图是由“○”和“□”组成的轴对称图形,则该图形的对称轴是直线( )
A.l1 B.l2 C.l3 D.l4
7. 如图,以C为圆心,大于点C到AB的距离为半径作弧,交AB于点D,E,再以D,E为圆心,大于DE的长为半径作弧,两弧交于点F,作射线CF,则( )
A.CF平分∠ACB B.CF⊥AB
C.CF平分AB D.CF垂直平分AB
8. 已知:在平面直角坐标系中,A(a,b)(b≠0),B(m,n).若a-m=4,b+n=0,则下列结论正确的是( )
A.把点A向左平移4个单位长度后,与点B关于x轴对称
B.把点A向右平移4个单位长度后,与点B关于x轴对称
C.把点A向左平移4个单位长度后,与点B关于y轴对称
D.把点A向右平移4个单位长度后,与点B关于y轴对称
9. 如图,分别以线段AB的两端点A,B为圆心,大于AB的长为半径画弧,在线段AB的两侧分别交于点E,F,作直线EF交AB于点O.在直线EF上任取一点P(不与点O重合),连接PA,PB,则下列结论不一定成立的是( )
A.PA=PB B.OA=OB
C.OP=OF D.PO⊥AB
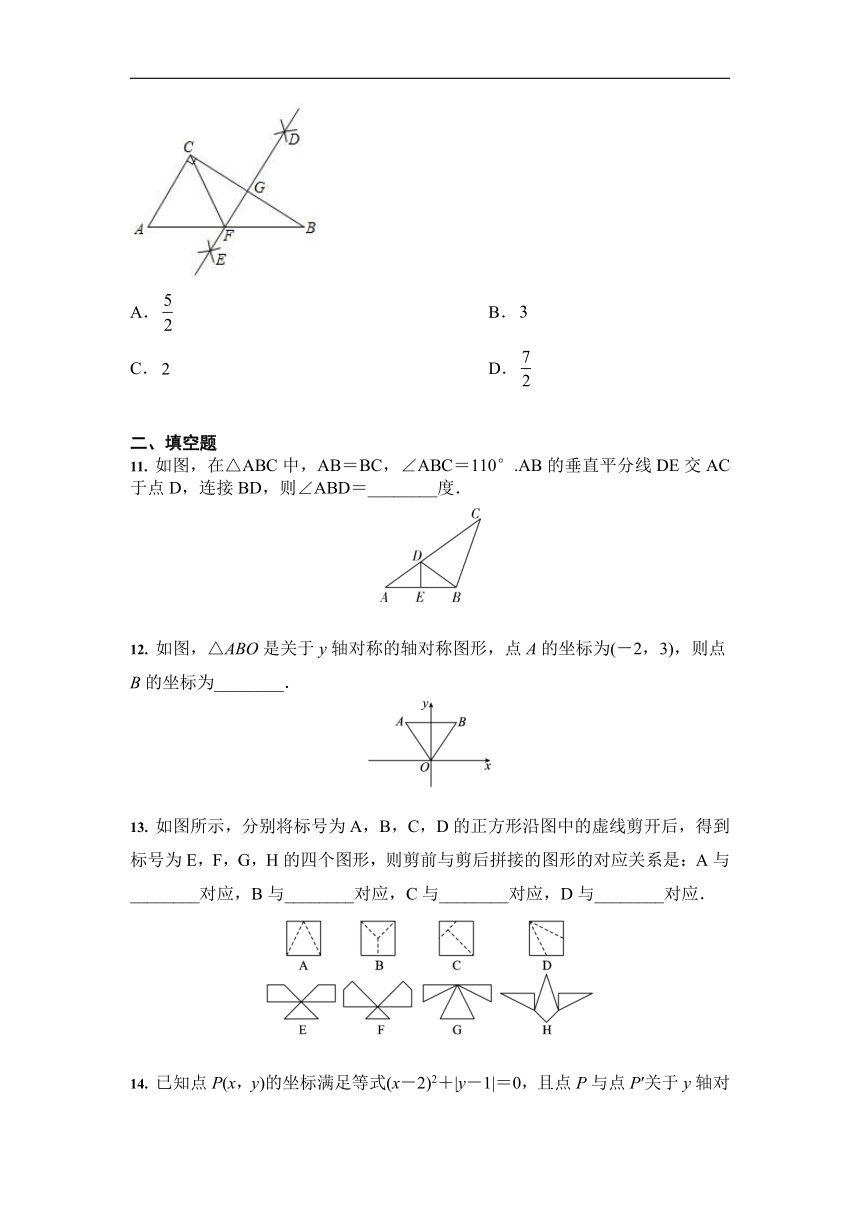
10. 如图,在中,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于两点,作直线交于点,交于点,连接.若,,则的长为
A. B.C. D.
二、填空题
11. 如图,在△ABC中,AB=BC,∠ABC=110°.AB的垂直平分线DE交AC于点D,连接BD,则∠ABD=________度.
12. 如图,△ABO是关于y轴对称的轴对称图形,点A的坐标为(-2,3),则点B的坐标为________.
13. 如图所示,分别将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为E,F,G,H的四个图形,则剪前与剪后拼接的图形的对应关系是:A与________对应,B与________对应,C与________对应,D与________对应.
14. 已知点P(x,y)的坐标满足等式(x-2)2+|y-1|=0,且点P与点P′关于y轴对称,则点P′的坐标为________.
15. 如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,AD恰好平分∠BAC.若DE=1,则BC的长是________.
16. 数学活动课上,两名同学围绕作图问题:“如图①,已知直线l和直线l外一点P,用直尺和圆规作直线PQ,使PQ⊥直线l于点Q.”分别作出了如图②③所示的两个图形,其中作法正确的为图 (填“②”或“③”).?
三、解答题
17. 如图所示,两个四边形关于直线l对称,∠C=90°,试写出边a,b的长,并求出∠G的度数.
18. 如图,在△ABC中,AB边的垂直平分线DE分别与AB边和AC边交于点D和点E,BC边的垂直平分线FG分别与BC边和AC边交于点F和点G,若△BEG的周长为16,GE=3,求AC的长.
19. 如图,在四边形ABCD中,AB=AD,BC边的垂直平分线MN经过点A.求证:点A在线段CD的垂直平分线上.
人教版 八年级数学上册 13.1 轴对称 同步训练-答案
一、选择题
1. 【答案】 B
2. 【答案】A
3. 【答案】B [解析] ∵点(m-1,-1)与点(5,-1)关于y轴对称,∴m-1=-5,解得m=-4.
4. 【答案】A
5. 【答案】D [解析] 点A(3,4)关于x轴的对称点A′的坐标为(3,-4),将点A′向左平移6个单位长度,得到点B(-3,-4).
6. 【答案】C [解析] 沿着直线l3折叠,直线两旁的部分能够互相重合,因此该图形的对称轴是直线l3.
7. 【答案】B
8. 【答案】A [解析] ∵a-m=4,∴a-4=m.
又∵b+n=0(b≠0),∴b=-n.
∴把点A向左平移4个单位长度后,与点B关于x轴对称.
9. 【答案】C [解析] 由作图可知,EF垂直平分AB,因此可得OA=OB,PO⊥AB,由线段垂直平分线的性质可得PA=PB,但不能得到OP=OF.
10. 【答案】A
【解析】由作法得垂直平分,
∴,,,
∵,∴,∴,
∴为斜边上的中线,
∵,
∴.故选A.
二、填空题
11. 【答案】35 【解析】∵AB=BC,∠ABC=110°,∴∠A=∠C=35°,∵DE垂直平分AB,∴DA=DB,∴∠ABD=∠A=35°.
12. 【答案】(2,3) [解析] ∵△ABO是关于y轴对称的轴对称图形,∴点A(-2,3)与点B关于y轴对称.∴点B的坐标为(2,3).
13. 【答案】G E F H [解析] A剪开后是三个三角形,B剪开后是两个直角梯形和一个三角形,C剪开后是一个直角三角形和两个四边形,D剪开后是两个三角形和一个四边形,因而,A与G对应,B与E对应,C与F对应,D与H对应.
14. 【答案】(-2,1) [解析] ∵(x-2)2≥0,|y-1|≥0,又(x-2)2+|y-1|=0,∴x-2=0且y-1=0,即x=2,y=1.∴点P的坐标为(2,1).那么点P关于y轴的对称点P′的坐标为(-2,1).
15. 【答案】3 [解析] ∵AD平分∠BAC,且DE⊥AB,∠C=90°,∴CD=DE=1.
∵DE是AB的垂直平分线,∴AD=BD.
∴∠B=∠DAB.
∵∠DAB=∠CAD,
∴∠CAD=∠DAB=∠B.
∵∠C=90°,∴∠CAD+∠DAB+∠B=90°.
∴∠B=30°.∴BD=2DE=2.
∴BC=BD+CD=2+1=3.
16. 【答案】③
三、解答题
17. 【答案】
解:∵两个四边形关于直线l对称,
∴四边形ABCD≌四边形FEHG,
∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,a=5 cm,b=4 cm.
∴∠G=360°-∠H-∠E-∠F=55°.
18. 【答案】
解:∵DE垂直平分线段AB,GF垂直平分线段BC,
∴EB=EA,GB=GC.
∵△BEG的周长为16,
∴EB+GB+GE=16.
∴EA+GC+GE=16.
∴GA+GE+GE+GE+EC=16.
∴AC+2GE=16.
∵GE=3,
∴AC=10.
19. 【答案】
证明:连接AC.
∵点A在线段BC的垂直平分线MN上,
∴AB=AC.
∵AB=AD,∴AC=AD.
∴点 A在线段CD的垂直平分线上.
一、选择题
1. 点M(3,2)关于x轴对称的点的坐标为 ( )
A. (-3,2) B. (3,-2) C. (-3,-2) D. (3,2)
2. 如图,线段AB与A′B′(AB=A′B′)不关于直线l成轴对称的是( )
3. 如果点(m-1,-1)与点(5,-1)关于y轴对称,那么m的值为( )
A.4 B.-4 C.5 D.-5
4. 将一张长与宽的比为2∶1的长方形纸片按图①②所示的方式对折,然后沿图③中的虚线裁剪,得到图④,最后将图④中的纸片展开铺平,所得到的图案是( )
5. 在平面直角坐标系中,作点A(3,4)关于x轴的对称点A′,再将点A′向左平移6个单位长度,得到点B,则点B的坐标为( )
A.(4,-3) B.(-4,3)
C.(-3,4) D.(-3,-4)
6. [2018·河北] 图是由“○”和“□”组成的轴对称图形,则该图形的对称轴是直线( )
A.l1 B.l2 C.l3 D.l4
7. 如图,以C为圆心,大于点C到AB的距离为半径作弧,交AB于点D,E,再以D,E为圆心,大于DE的长为半径作弧,两弧交于点F,作射线CF,则( )
A.CF平分∠ACB B.CF⊥AB
C.CF平分AB D.CF垂直平分AB
8. 已知:在平面直角坐标系中,A(a,b)(b≠0),B(m,n).若a-m=4,b+n=0,则下列结论正确的是( )
A.把点A向左平移4个单位长度后,与点B关于x轴对称
B.把点A向右平移4个单位长度后,与点B关于x轴对称
C.把点A向左平移4个单位长度后,与点B关于y轴对称
D.把点A向右平移4个单位长度后,与点B关于y轴对称
9. 如图,分别以线段AB的两端点A,B为圆心,大于AB的长为半径画弧,在线段AB的两侧分别交于点E,F,作直线EF交AB于点O.在直线EF上任取一点P(不与点O重合),连接PA,PB,则下列结论不一定成立的是( )
A.PA=PB B.OA=OB
C.OP=OF D.PO⊥AB
10. 如图,在中,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于两点,作直线交于点,交于点,连接.若,,则的长为
A. B.C. D.
二、填空题
11. 如图,在△ABC中,AB=BC,∠ABC=110°.AB的垂直平分线DE交AC于点D,连接BD,则∠ABD=________度.
12. 如图,△ABO是关于y轴对称的轴对称图形,点A的坐标为(-2,3),则点B的坐标为________.
13. 如图所示,分别将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为E,F,G,H的四个图形,则剪前与剪后拼接的图形的对应关系是:A与________对应,B与________对应,C与________对应,D与________对应.
14. 已知点P(x,y)的坐标满足等式(x-2)2+|y-1|=0,且点P与点P′关于y轴对称,则点P′的坐标为________.
15. 如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,AD恰好平分∠BAC.若DE=1,则BC的长是________.
16. 数学活动课上,两名同学围绕作图问题:“如图①,已知直线l和直线l外一点P,用直尺和圆规作直线PQ,使PQ⊥直线l于点Q.”分别作出了如图②③所示的两个图形,其中作法正确的为图 (填“②”或“③”).?
三、解答题
17. 如图所示,两个四边形关于直线l对称,∠C=90°,试写出边a,b的长,并求出∠G的度数.
18. 如图,在△ABC中,AB边的垂直平分线DE分别与AB边和AC边交于点D和点E,BC边的垂直平分线FG分别与BC边和AC边交于点F和点G,若△BEG的周长为16,GE=3,求AC的长.
19. 如图,在四边形ABCD中,AB=AD,BC边的垂直平分线MN经过点A.求证:点A在线段CD的垂直平分线上.
人教版 八年级数学上册 13.1 轴对称 同步训练-答案
一、选择题
1. 【答案】 B
2. 【答案】A
3. 【答案】B [解析] ∵点(m-1,-1)与点(5,-1)关于y轴对称,∴m-1=-5,解得m=-4.
4. 【答案】A
5. 【答案】D [解析] 点A(3,4)关于x轴的对称点A′的坐标为(3,-4),将点A′向左平移6个单位长度,得到点B(-3,-4).
6. 【答案】C [解析] 沿着直线l3折叠,直线两旁的部分能够互相重合,因此该图形的对称轴是直线l3.
7. 【答案】B
8. 【答案】A [解析] ∵a-m=4,∴a-4=m.
又∵b+n=0(b≠0),∴b=-n.
∴把点A向左平移4个单位长度后,与点B关于x轴对称.
9. 【答案】C [解析] 由作图可知,EF垂直平分AB,因此可得OA=OB,PO⊥AB,由线段垂直平分线的性质可得PA=PB,但不能得到OP=OF.
10. 【答案】A
【解析】由作法得垂直平分,
∴,,,
∵,∴,∴,
∴为斜边上的中线,
∵,
∴.故选A.
二、填空题
11. 【答案】35 【解析】∵AB=BC,∠ABC=110°,∴∠A=∠C=35°,∵DE垂直平分AB,∴DA=DB,∴∠ABD=∠A=35°.
12. 【答案】(2,3) [解析] ∵△ABO是关于y轴对称的轴对称图形,∴点A(-2,3)与点B关于y轴对称.∴点B的坐标为(2,3).
13. 【答案】G E F H [解析] A剪开后是三个三角形,B剪开后是两个直角梯形和一个三角形,C剪开后是一个直角三角形和两个四边形,D剪开后是两个三角形和一个四边形,因而,A与G对应,B与E对应,C与F对应,D与H对应.
14. 【答案】(-2,1) [解析] ∵(x-2)2≥0,|y-1|≥0,又(x-2)2+|y-1|=0,∴x-2=0且y-1=0,即x=2,y=1.∴点P的坐标为(2,1).那么点P关于y轴的对称点P′的坐标为(-2,1).
15. 【答案】3 [解析] ∵AD平分∠BAC,且DE⊥AB,∠C=90°,∴CD=DE=1.
∵DE是AB的垂直平分线,∴AD=BD.
∴∠B=∠DAB.
∵∠DAB=∠CAD,
∴∠CAD=∠DAB=∠B.
∵∠C=90°,∴∠CAD+∠DAB+∠B=90°.
∴∠B=30°.∴BD=2DE=2.
∴BC=BD+CD=2+1=3.
16. 【答案】③
三、解答题
17. 【答案】
解:∵两个四边形关于直线l对称,
∴四边形ABCD≌四边形FEHG,
∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,a=5 cm,b=4 cm.
∴∠G=360°-∠H-∠E-∠F=55°.
18. 【答案】
解:∵DE垂直平分线段AB,GF垂直平分线段BC,
∴EB=EA,GB=GC.
∵△BEG的周长为16,
∴EB+GB+GE=16.
∴EA+GC+GE=16.
∴GA+GE+GE+GE+EC=16.
∴AC+2GE=16.
∵GE=3,
∴AC=10.
19. 【答案】
证明:连接AC.
∵点A在线段BC的垂直平分线MN上,
∴AB=AC.
∵AB=AD,∴AC=AD.
∴点 A在线段CD的垂直平分线上.
