人教版 九年级数学 23.1 图形的旋转 课后训练(Word版 含答案)
文档属性
| 名称 | 人教版 九年级数学 23.1 图形的旋转 课后训练(Word版 含答案) | 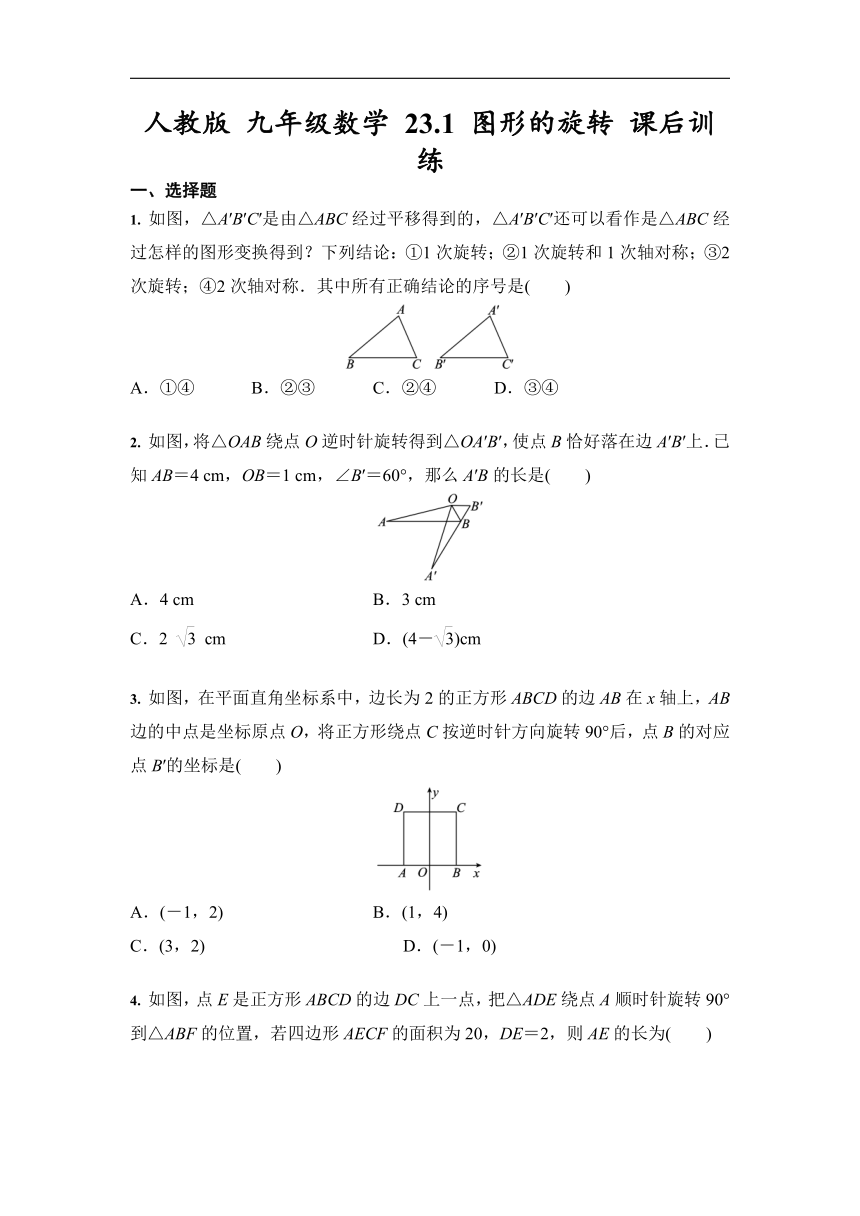 | |
| 格式 | doc | ||
| 文件大小 | 486.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-14 23:59:33 | ||
图片预览




文档简介
人教版 九年级数学 23.1 图形的旋转 课后训练
一、选择题
1. 如图,△A′B′C′是由△ABC经过平移得到的,△A′B′C′还可以看作是△ABC经过怎样的图形变换得到?下列结论:①1次旋转;②1次旋转和1次轴对称;③2次旋转;④2次轴对称.其中所有正确结论的序号是( )
A.①④ B.②③ C.②④ D.③④
2. 如图,将△OAB绕点O逆时针旋转得到△OA′B′,使点B恰好落在边A′B′上.已知AB=4 cm,OB=1 cm,∠B′=60°,那么A′B的长是( )
A.4 cm B.3 cm
C.2 cm D.(4-)cm
3. 如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB边的中点是坐标原点O,将正方形绕点C按逆时针方向旋转90°后,点B的对应点B′的坐标是( )
A.(-1,2) B.(1,4)
C.(3,2) D.(-1,0)
4. 如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为20,DE=2,则AE的长为( )
A.4 B.2
C.6 D.2
5. 如图,Rt△OCB的斜边在y轴上,OC=,含30°角的顶点与原点重合,直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′,则点B的对应点B′的坐标是( )
A.(,-1) B.(1,-)
C.(2,0) D.(,0)
6. 如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列结论一定正确的是( )
A.AC=AD B.AB⊥EB
C.BC=DE D.∠A=∠EBC
7. 如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°-α B.α C.180°-α D.2α
8. 2019·河南 如图,在△OAB中,顶点O(0,0),A(-3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第70次旋转结束时,点D的坐标为( )
A.(10,3) B.(-3,10) C.(10,-3) D.(3,-10)
二、填空题
9. 如图,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心点O至少经过______次旋转而得到,每一次旋转______度.
10. 如图所示,△ABC的顶点都在网格线的交点(格点)上,如果将△ABC绕点C逆时针旋转90°,那么点B的对应点B′的坐标是________.
11. 如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=________°.
12. 如图,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为________.
13. 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为________.
14. 2018·陕西 如图,点O是平行四边形ABCD的对称中心,AD>AB,E,F是AB边上的点,且EF=AB;G,H是BC边上的点,且GH=BC.若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是=________.
15. 如图,AB⊥y轴,将△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=-x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=-x上,依次进行下去……若点B的坐标是(0,1),则点O12的纵坐标为________.
三、解答题
16. 如图,P为正方形ABCD内一点,若PA=a,PB=2a,PC=3a(a>0).
(1)求∠APB的度数;
(2)求正方形ABCD的面积.
17. 如图,在等边三角形ABC内有一点P,且PA=2,PB=,PC=1.求∠BPC的度数和等边三角形ABC的边长.
18. 已知:如图,在四边形ABCD中,∠ADC=60°,∠ABC=30°,AD=CD.
求证:BD2=AB2+BC2.
人教版 九年级数学 23.1 图形的旋转 课后训练-答案
一、选择题
1. 【答案】D [解析] 先将△ABC绕着B′C的中点旋转180°,再将所得的三角形绕着B′C′的中点旋转180°,即可得到△A′B′C′;先将△ABC沿着B′C的垂直平分线翻折,再将所得的三角形沿着B′C′的垂直平分线翻折,即可得到△A′B′C′.故选D.
2. 【答案】B [解析] ∵旋转前、后的两个图形是全等图形,AB=4 cm,OB=1 cm,∴A′B′=AB=4 cm,OB′=OB=1 cm.
在△OB′B中,∵∠B′=60°,OB′=OB,
∴△OB′B是等边三角形,∴BB′=OB=1 cm,
∴A′B=A′B′-BB′=4-1=3(cm).
3. 【答案】C
4. 【答案】D [解析] 由旋转可得,S正方形ABCD=S四边形AECF=20,即AD2=20,∴AD=2 .
∵DE=2,∴在Rt△ADE中,AE==2 .故选D.
5. 【答案】A
6. 【答案】D [解析] 由旋转的性质可知,AC=CD,但∠A不一定是60°,所以不能证明AC=AD,所以选项A错误;因为旋转角度不定,所以选项B不能确定;因为不确定AB和BC的数量关系,所以BC和DE的数量关系不能确定,所以选项C不能确定;由旋转的性质可知∠ACD=∠BCE,AC=DC,BC=EC,所以2∠A=180°-∠ACD,2∠EBC=180°-∠BCE,从而可证选项D是正确的.
7. 【答案】C [解析] 由题意可得∠CBD=α,∠C=∠EDB.
∵∠EDB+∠ADB=180°,
∴∠C+∠ADB=180°.
由四边形的内角和定理,得∠CAD+∠CBD=180°.
∴∠CAD=180°-∠CBD=180°-α.故选C.
8. 【答案】D
二、填空题
9. 【答案】4 72
10. 【答案】(1,0)
11. 【答案】20 [解析] ∵AB=AB′,∠BAB′=40°,
∴∠ABB′=70°.∵B′C′⊥AB,∴∠BB′C′=20°.
12. 【答案】15° [解析] 由旋转的性质可知AB=AD,
∠BAD=150°,∴∠B=∠ADB=×(180°-150°)=15°.
13. 【答案】18 [解析] 如图.∵∠BAD=∠BCD=90°,∴∠B+∠ADC=180°.又∵AB=AD,∴将△ABC绕点A逆时针旋转90°后点B与点D重合,点C的对应点E落在CD的延长线上,∴AE=AC=6,∠CAE=90°,∴S四边形ABCD=S△ACE=AC·AE=×6×6=18.
14. 【答案】 [解析] ∵==,==,
∴S1=S△AOB,S2=S△BOC.
∵点O是?ABCD的对称中心,
∴S△AOB=S△BOC=S平行四边形ABCD,∴=.
15. 【答案】9+3 [解析] 将y=1代入y=-x,解得x=-.
∴AB=,OA=2,且直线y=-x与x轴所夹的锐角是30°.
由图可知,在旋转过程中每3次一循环,其中OO2=O2O4=O4O6=O6O8=O8O10=O10O12=2++1=3+.
∴OO12=6×(3+)=18+6 .
∴点O12的纵坐标=OO12=9+3 .
三、解答题
16. 【答案】
解:(1)将△ABP绕点B顺时针旋转90°得到△CBQ,连接PQ,如图,
则∠APB=∠BQC,PB⊥QB,PB=QB=2a,
AP=QC=a,
∴PQ=2 a.
在△PQC中,∵PC2=9a2,PQ2+QC2=9a2,∴PC2=PQ2+QC2,
∴△PQC为直角三角形且∠PQC=90°.
∵△PBQ是等腰直角三角形,
∴∠BPQ=∠BQP=45°,
故∠APB=∠CQB=90°+45°=135°.
(2)连接AC.
∵∠APQ=∠APB+∠BPQ=135°+45°=180°,
∴A,P,Q三点在同一条直线上.
在Rt△AQC中,AC2=AQ2+QC2=(a+2 a)2+a2=(10+4 )a2,
∴正方形ABCD的面积S=AB2==(5+2 )a2.
17. 【答案】
解:将△BPC绕点B逆时针旋转60°得到△BP′A(如图).连接PP′,由旋转的性质知△BPP′为等边三角形,AP′=PC=1,
∴PP′=PB=,∠BPP′=∠BP′P=60°.
在△APP′中,∵AP′2+PP′2=12+()2=22=PA2,
∴△APP′是直角三角形,且∠AP′P=90°,
∴∠BP′A=∠BP′P+∠AP′P=60°+90°=150°,
∴∠BPC=∠BP′A=150°.
在Rt△APP′中,∵PA=2,AP′=1,
∴∠APP′=30°.
又∵∠BPP′=60°,
∴∠APB=90°,
∴在Rt△ABP中,AB===,
即等边三角形ABC的边长为.
18. 【答案】
证明:如图,将△ADB绕点D顺时针旋转60°,得到△CDE,连接BE,
则∠ADB=∠CDE,∠A=∠DCE,AB=CE,BD=DE.
又∵∠ADC=60°,∴∠BDE=60°,
∴△DBE是等边三角形,
∴BD=BE.
又∵∠ECB=360°-∠BCD-∠DCE=360°-∠BCD-∠A=360°-(360°-∠ADC-∠ABC)=90°,
∴△ECB是直角三角形,
∴BE2=CE2+BC2,即BD2=AB2+BC2.
一、选择题
1. 如图,△A′B′C′是由△ABC经过平移得到的,△A′B′C′还可以看作是△ABC经过怎样的图形变换得到?下列结论:①1次旋转;②1次旋转和1次轴对称;③2次旋转;④2次轴对称.其中所有正确结论的序号是( )
A.①④ B.②③ C.②④ D.③④
2. 如图,将△OAB绕点O逆时针旋转得到△OA′B′,使点B恰好落在边A′B′上.已知AB=4 cm,OB=1 cm,∠B′=60°,那么A′B的长是( )
A.4 cm B.3 cm
C.2 cm D.(4-)cm
3. 如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB边的中点是坐标原点O,将正方形绕点C按逆时针方向旋转90°后,点B的对应点B′的坐标是( )
A.(-1,2) B.(1,4)
C.(3,2) D.(-1,0)
4. 如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为20,DE=2,则AE的长为( )
A.4 B.2
C.6 D.2
5. 如图,Rt△OCB的斜边在y轴上,OC=,含30°角的顶点与原点重合,直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′,则点B的对应点B′的坐标是( )
A.(,-1) B.(1,-)
C.(2,0) D.(,0)
6. 如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列结论一定正确的是( )
A.AC=AD B.AB⊥EB
C.BC=DE D.∠A=∠EBC
7. 如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°-α B.α C.180°-α D.2α
8. 2019·河南 如图,在△OAB中,顶点O(0,0),A(-3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第70次旋转结束时,点D的坐标为( )
A.(10,3) B.(-3,10) C.(10,-3) D.(3,-10)
二、填空题
9. 如图,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心点O至少经过______次旋转而得到,每一次旋转______度.
10. 如图所示,△ABC的顶点都在网格线的交点(格点)上,如果将△ABC绕点C逆时针旋转90°,那么点B的对应点B′的坐标是________.
11. 如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=________°.
12. 如图,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为________.
13. 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为________.
14. 2018·陕西 如图,点O是平行四边形ABCD的对称中心,AD>AB,E,F是AB边上的点,且EF=AB;G,H是BC边上的点,且GH=BC.若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是=________.
15. 如图,AB⊥y轴,将△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=-x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=-x上,依次进行下去……若点B的坐标是(0,1),则点O12的纵坐标为________.
三、解答题
16. 如图,P为正方形ABCD内一点,若PA=a,PB=2a,PC=3a(a>0).
(1)求∠APB的度数;
(2)求正方形ABCD的面积.
17. 如图,在等边三角形ABC内有一点P,且PA=2,PB=,PC=1.求∠BPC的度数和等边三角形ABC的边长.
18. 已知:如图,在四边形ABCD中,∠ADC=60°,∠ABC=30°,AD=CD.
求证:BD2=AB2+BC2.
人教版 九年级数学 23.1 图形的旋转 课后训练-答案
一、选择题
1. 【答案】D [解析] 先将△ABC绕着B′C的中点旋转180°,再将所得的三角形绕着B′C′的中点旋转180°,即可得到△A′B′C′;先将△ABC沿着B′C的垂直平分线翻折,再将所得的三角形沿着B′C′的垂直平分线翻折,即可得到△A′B′C′.故选D.
2. 【答案】B [解析] ∵旋转前、后的两个图形是全等图形,AB=4 cm,OB=1 cm,∴A′B′=AB=4 cm,OB′=OB=1 cm.
在△OB′B中,∵∠B′=60°,OB′=OB,
∴△OB′B是等边三角形,∴BB′=OB=1 cm,
∴A′B=A′B′-BB′=4-1=3(cm).
3. 【答案】C
4. 【答案】D [解析] 由旋转可得,S正方形ABCD=S四边形AECF=20,即AD2=20,∴AD=2 .
∵DE=2,∴在Rt△ADE中,AE==2 .故选D.
5. 【答案】A
6. 【答案】D [解析] 由旋转的性质可知,AC=CD,但∠A不一定是60°,所以不能证明AC=AD,所以选项A错误;因为旋转角度不定,所以选项B不能确定;因为不确定AB和BC的数量关系,所以BC和DE的数量关系不能确定,所以选项C不能确定;由旋转的性质可知∠ACD=∠BCE,AC=DC,BC=EC,所以2∠A=180°-∠ACD,2∠EBC=180°-∠BCE,从而可证选项D是正确的.
7. 【答案】C [解析] 由题意可得∠CBD=α,∠C=∠EDB.
∵∠EDB+∠ADB=180°,
∴∠C+∠ADB=180°.
由四边形的内角和定理,得∠CAD+∠CBD=180°.
∴∠CAD=180°-∠CBD=180°-α.故选C.
8. 【答案】D
二、填空题
9. 【答案】4 72
10. 【答案】(1,0)
11. 【答案】20 [解析] ∵AB=AB′,∠BAB′=40°,
∴∠ABB′=70°.∵B′C′⊥AB,∴∠BB′C′=20°.
12. 【答案】15° [解析] 由旋转的性质可知AB=AD,
∠BAD=150°,∴∠B=∠ADB=×(180°-150°)=15°.
13. 【答案】18 [解析] 如图.∵∠BAD=∠BCD=90°,∴∠B+∠ADC=180°.又∵AB=AD,∴将△ABC绕点A逆时针旋转90°后点B与点D重合,点C的对应点E落在CD的延长线上,∴AE=AC=6,∠CAE=90°,∴S四边形ABCD=S△ACE=AC·AE=×6×6=18.
14. 【答案】 [解析] ∵==,==,
∴S1=S△AOB,S2=S△BOC.
∵点O是?ABCD的对称中心,
∴S△AOB=S△BOC=S平行四边形ABCD,∴=.
15. 【答案】9+3 [解析] 将y=1代入y=-x,解得x=-.
∴AB=,OA=2,且直线y=-x与x轴所夹的锐角是30°.
由图可知,在旋转过程中每3次一循环,其中OO2=O2O4=O4O6=O6O8=O8O10=O10O12=2++1=3+.
∴OO12=6×(3+)=18+6 .
∴点O12的纵坐标=OO12=9+3 .
三、解答题
16. 【答案】
解:(1)将△ABP绕点B顺时针旋转90°得到△CBQ,连接PQ,如图,
则∠APB=∠BQC,PB⊥QB,PB=QB=2a,
AP=QC=a,
∴PQ=2 a.
在△PQC中,∵PC2=9a2,PQ2+QC2=9a2,∴PC2=PQ2+QC2,
∴△PQC为直角三角形且∠PQC=90°.
∵△PBQ是等腰直角三角形,
∴∠BPQ=∠BQP=45°,
故∠APB=∠CQB=90°+45°=135°.
(2)连接AC.
∵∠APQ=∠APB+∠BPQ=135°+45°=180°,
∴A,P,Q三点在同一条直线上.
在Rt△AQC中,AC2=AQ2+QC2=(a+2 a)2+a2=(10+4 )a2,
∴正方形ABCD的面积S=AB2==(5+2 )a2.
17. 【答案】
解:将△BPC绕点B逆时针旋转60°得到△BP′A(如图).连接PP′,由旋转的性质知△BPP′为等边三角形,AP′=PC=1,
∴PP′=PB=,∠BPP′=∠BP′P=60°.
在△APP′中,∵AP′2+PP′2=12+()2=22=PA2,
∴△APP′是直角三角形,且∠AP′P=90°,
∴∠BP′A=∠BP′P+∠AP′P=60°+90°=150°,
∴∠BPC=∠BP′A=150°.
在Rt△APP′中,∵PA=2,AP′=1,
∴∠APP′=30°.
又∵∠BPP′=60°,
∴∠APB=90°,
∴在Rt△ABP中,AB===,
即等边三角形ABC的边长为.
18. 【答案】
证明:如图,将△ADB绕点D顺时针旋转60°,得到△CDE,连接BE,
则∠ADB=∠CDE,∠A=∠DCE,AB=CE,BD=DE.
又∵∠ADC=60°,∴∠BDE=60°,
∴△DBE是等边三角形,
∴BD=BE.
又∵∠ECB=360°-∠BCD-∠DCE=360°-∠BCD-∠A=360°-(360°-∠ADC-∠ABC)=90°,
∴△ECB是直角三角形,
∴BE2=CE2+BC2,即BD2=AB2+BC2.
同课章节目录
