人教版 九年级数学 23.2 中心对称 课后训练(Word版 含答案)
文档属性
| 名称 | 人教版 九年级数学 23.2 中心对称 课后训练(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 662.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-15 00:04:25 | ||
图片预览



文档简介
人教版 九年级数学 23.2 中心对称 课后训练
一、选择题
1. 下列四个银行标志中,既是中心对称图形,又是轴对称图形的是( )
2. 如图,△DEF是由△ABC绕点O旋转180°得到的,则下列结论不成立的是( )
A.点A与点D是对称点 B.BO=EO
C.∠ACB=∠FDE D.AB∥DE
3. 2019·长春德惠期末 如图,△ABC与△A′B′C′关于点O中心对称,下列结论中不一定成立的是( )
A.∠ABC=∠A′C′B′ B.OA=OA′
C.BC=B′C′ D.OC=OC′
4. 如图,两个半圆分别以P,O为圆心,它们成中心对称,点A1,P,B1,B2,O,A2在同一条直线上,则对称中心为( )
A.A2P的中点 B.A1B2的中点
C.A1O的中点 D.PO的中点
5. 把△ABC各点的横坐标都乘-1,纵坐标都乘-1,符合上述要求的图是( )
6. 如图,已知菱形ABCD与菱形EFGH关于直线BD上的某个点中心对称,则点B的对称点是( )
A.点E B.点F
C.点G D.点H
7. 如图,将△ABC以点O为旋转中心旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后变为线段E′D′.已知BC=4,则线段E′D′的长度为( )
A.2 B.3 C.4 D.1.5
8. 在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1对称,再作△B2A3B3与△B2A2B1关于点B2对称……如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
A.(4n-1,) B.(2n-1,)
C.(4n+1,) D.(2n+1,)
二、填空题
9. 王老师、杨老师两家所在的位置关于学校对称.如果王老师家距学校2千米,那么他们两家相距________千米.
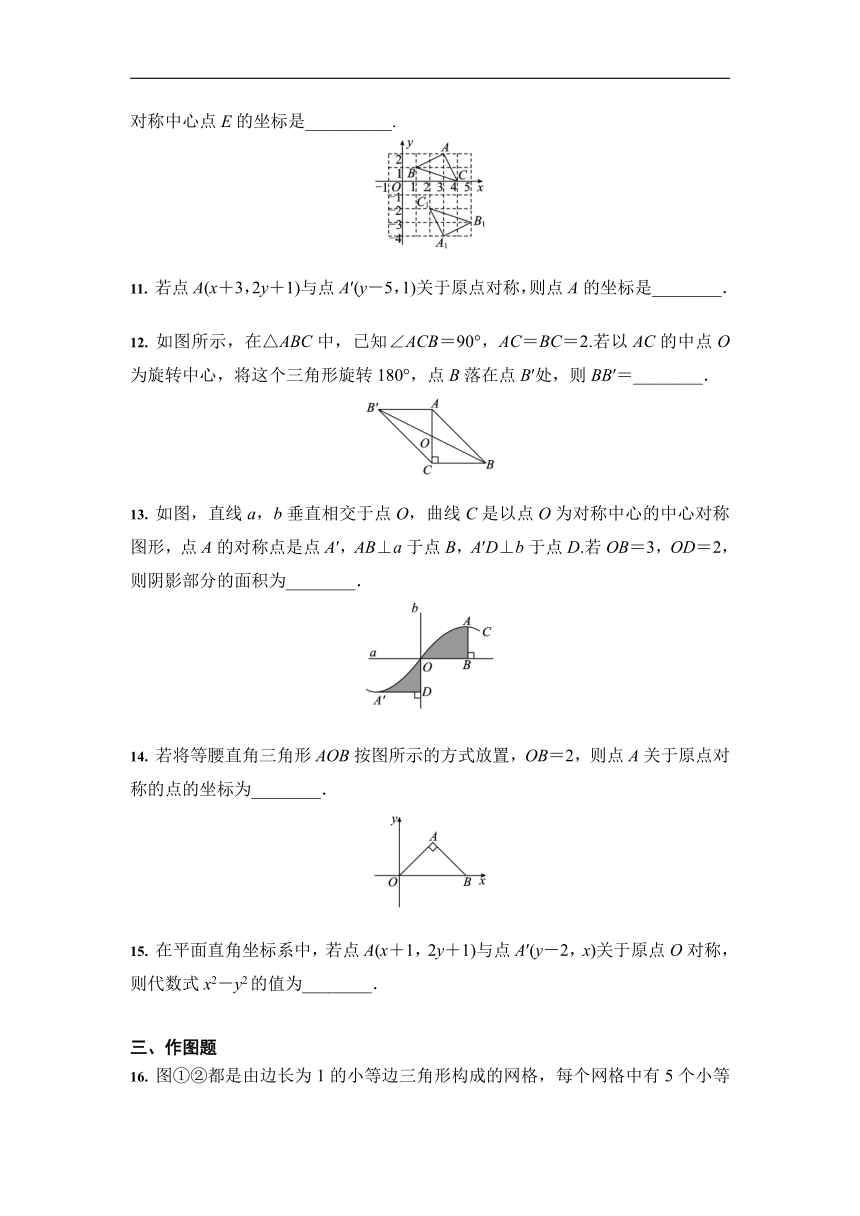
10. 如图所示, 在平面直角坐标系中, 若△ABC与△A1B1C1关于点E对称, 则对称中心点E的坐标是__________.
11. 若点A(x+3,2y+1)与点A′(y-5,1)关于原点对称,则点A的坐标是________.
12. 如图所示,在△ABC中,已知∠ACB=90°,AC=BC=2.若以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,则BB′=________.
13. 如图,直线a,b垂直相交于点O,曲线C是以点O为对称中心的中心对称图形,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D.若OB=3,OD=2,则阴影部分的面积为________.
14. 若将等腰直角三角形AOB按图所示的方式放置,OB=2,则点A关于原点对称的点的坐标为________.
15. 在平面直角坐标系中,若点A(x+1,2y+1)与点A′(y-2,x)关于原点O对称,则代数式x2-y2的值为________.
三、作图题
16. 图①②都是由边长为1的小等边三角形构成的网格,每个网格中有5个小等边三角形已涂上阴影,请在余下的空白小等边三角形中,按下列要求选取一个涂上阴影:
(1)使得6个阴影小等边三角形组成一个轴对称图形;
(2)使得6个阴影小等边三角形组成一个中心对称图形.
(请将两个小题依次作答在图①②中,均只需画出符合条件的一种情形)
17. 如图,画出与△ABC关于点O中心对称的△A′B′C′.
四、解答题
18. 如图,在正方形网格中,△ABC的三个顶点都在格点上,点A,B,C的坐标分别为(-2,4),(-2,0),(-4,1),结合所给的平面直角坐标系解答下列问题:
(1)画出△ABC关于原点O对称的△A1B1C1;
(2)平移△ABC,使点A移动到点A2(0,2)的位置,画出平移后的△A2B2C2,并写出点B2,C2的坐标;
(3)在△ABC,△A1B1C1中,△A2B2C2与________成中心对称,其对称中心的坐标为________.
19. 2018·眉山 在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点C1的坐标;
(2)作出△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标;
(3)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(-4,-2),请直接写出直线l的函数解析式.
20. 如图,已知△ABC和点O.
(1)在图中画出△A′B′C′,使△A′B′C′与△ABC关于点O对称;
(2)点A,B,C,A′,B′,C′能组成哪几个平行四边形?请用符号表示出来.
人教版 九年级数学 23.2 中心对称 课后训练-答案
一、选择题
1. 【答案】C
2. 【答案】C [解析] 根据旋转的性质可知,点A与点D是对称点,BO=EO,AB∥DE,∠ACB=∠DFE≠∠FDE.故选C.
3. 【答案】A
4. 【答案】D [解析] 因为P,O是对称点,所以PO的中点是对称中心.
5. 【答案】C
6. 【答案】D [解析] 由于点B,D,F,H在同一条直线上,根据中心对称的定义可知,只能是点B和点H是对称点,点F和点D是对称点.故选D.
7. 【答案】A [解析] ∵ED是△ABC的中位线,BC=4,∴ED=2.又∵△A′B′C′和△ABC关于点O中心对称,∴E′D′=ED=2.
8. 【答案】C [解析] A1(1,),A2(3,-),A3(5,),A4(7,-),…,
∴点An的坐标为
∵2n+1是奇数,∴点A2n+1的坐标是(4n+1,).故选C.
二、填空题
9. 【答案】4 [解析] ∵王老师、杨老师两家所在的位置关于学校对称,
∴王老师、杨老师两家到学校的距离相等.
∵王老师家距学校2千米,
∴他们两家相距4千米.
故答案为4.
10. 【答案】(3,-1) [解析] 连接各组对应点,其交点坐标即为对称中心点E的坐标.
11. 【答案】(6,-1) [解析] 依题意,得解得∴点A的坐标为(6,-1).
12. 【答案】2 [解析] ∵△ABC绕AC的中点O旋转了180°,
∴OB=OB′,∴BB′=2OB.
又∵OC=OA=AC=1,BC=2,
∴在Rt△OBC中,OB===,
∴BB′=2OB=2 .
13. 【答案】6 [解析] 如图,过点A′作A′B′⊥a,垂足为B′,由题意可知,①与②关于点O中心对称,所以阴影部分的面积可以看作四边形A′B′OD的面积.又A′D⊥b于点D,直线a,b互相垂直,可得四边形A′B′OD是矩形,所以其面积为3×2=6.
14. 【答案】(-1,-1) [解析] 如图,过点A作AD⊥OB于点D.∵△AOB是等腰直角三角形,OB=2,∴OD=AD=1,∴A(1,1),∴点A关于原点对称的点的坐标为(-1,-1).
15. 【答案】5 [解析] ∵点A(x+1,2y+1)与点A′(y-2,x)关于原点O对称,
∴解得
故x2-y2=9-4=5.
故答案为5.
三、作图题
16. 【答案】
解:(1)答案不唯一,画出下列其中一种即可.
(2)答案不唯一,画出下列其中一种即可.
17. 【答案】
解:如图,△A′B′C′即为所求.
四、解答题
18. 【答案】
解:(1)△ABC关于原点O对称的△A1B1C1如图所示.
(2)平移后的△A2B2C2如图所示,其中点B2的坐标为(0,-2),点C2的坐标为(-2,-1).
(3)△A1B1C1 (1,-1)
19. 【答案】
解:(1)如图,△A1B1C1为所作,C1(-1,2).
(2)如图,△A2B2C2为所作,C2(-3,-2).
(3)因为点A的坐标为(2,4),点A3的坐标为(-4,-2),
所以直线l的函数解析式为y=-x.
20. 【答案】
解:(1)如图所示.
(2)?ABA′B′,?BCB′C′,?CA′C′A.
一、选择题
1. 下列四个银行标志中,既是中心对称图形,又是轴对称图形的是( )
2. 如图,△DEF是由△ABC绕点O旋转180°得到的,则下列结论不成立的是( )
A.点A与点D是对称点 B.BO=EO
C.∠ACB=∠FDE D.AB∥DE
3. 2019·长春德惠期末 如图,△ABC与△A′B′C′关于点O中心对称,下列结论中不一定成立的是( )
A.∠ABC=∠A′C′B′ B.OA=OA′
C.BC=B′C′ D.OC=OC′
4. 如图,两个半圆分别以P,O为圆心,它们成中心对称,点A1,P,B1,B2,O,A2在同一条直线上,则对称中心为( )
A.A2P的中点 B.A1B2的中点
C.A1O的中点 D.PO的中点
5. 把△ABC各点的横坐标都乘-1,纵坐标都乘-1,符合上述要求的图是( )
6. 如图,已知菱形ABCD与菱形EFGH关于直线BD上的某个点中心对称,则点B的对称点是( )
A.点E B.点F
C.点G D.点H
7. 如图,将△ABC以点O为旋转中心旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后变为线段E′D′.已知BC=4,则线段E′D′的长度为( )
A.2 B.3 C.4 D.1.5
8. 在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1对称,再作△B2A3B3与△B2A2B1关于点B2对称……如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
A.(4n-1,) B.(2n-1,)
C.(4n+1,) D.(2n+1,)
二、填空题
9. 王老师、杨老师两家所在的位置关于学校对称.如果王老师家距学校2千米,那么他们两家相距________千米.
10. 如图所示, 在平面直角坐标系中, 若△ABC与△A1B1C1关于点E对称, 则对称中心点E的坐标是__________.
11. 若点A(x+3,2y+1)与点A′(y-5,1)关于原点对称,则点A的坐标是________.
12. 如图所示,在△ABC中,已知∠ACB=90°,AC=BC=2.若以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,则BB′=________.
13. 如图,直线a,b垂直相交于点O,曲线C是以点O为对称中心的中心对称图形,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D.若OB=3,OD=2,则阴影部分的面积为________.
14. 若将等腰直角三角形AOB按图所示的方式放置,OB=2,则点A关于原点对称的点的坐标为________.
15. 在平面直角坐标系中,若点A(x+1,2y+1)与点A′(y-2,x)关于原点O对称,则代数式x2-y2的值为________.
三、作图题
16. 图①②都是由边长为1的小等边三角形构成的网格,每个网格中有5个小等边三角形已涂上阴影,请在余下的空白小等边三角形中,按下列要求选取一个涂上阴影:
(1)使得6个阴影小等边三角形组成一个轴对称图形;
(2)使得6个阴影小等边三角形组成一个中心对称图形.
(请将两个小题依次作答在图①②中,均只需画出符合条件的一种情形)
17. 如图,画出与△ABC关于点O中心对称的△A′B′C′.
四、解答题
18. 如图,在正方形网格中,△ABC的三个顶点都在格点上,点A,B,C的坐标分别为(-2,4),(-2,0),(-4,1),结合所给的平面直角坐标系解答下列问题:
(1)画出△ABC关于原点O对称的△A1B1C1;
(2)平移△ABC,使点A移动到点A2(0,2)的位置,画出平移后的△A2B2C2,并写出点B2,C2的坐标;
(3)在△ABC,△A1B1C1中,△A2B2C2与________成中心对称,其对称中心的坐标为________.
19. 2018·眉山 在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点C1的坐标;
(2)作出△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标;
(3)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(-4,-2),请直接写出直线l的函数解析式.
20. 如图,已知△ABC和点O.
(1)在图中画出△A′B′C′,使△A′B′C′与△ABC关于点O对称;
(2)点A,B,C,A′,B′,C′能组成哪几个平行四边形?请用符号表示出来.
人教版 九年级数学 23.2 中心对称 课后训练-答案
一、选择题
1. 【答案】C
2. 【答案】C [解析] 根据旋转的性质可知,点A与点D是对称点,BO=EO,AB∥DE,∠ACB=∠DFE≠∠FDE.故选C.
3. 【答案】A
4. 【答案】D [解析] 因为P,O是对称点,所以PO的中点是对称中心.
5. 【答案】C
6. 【答案】D [解析] 由于点B,D,F,H在同一条直线上,根据中心对称的定义可知,只能是点B和点H是对称点,点F和点D是对称点.故选D.
7. 【答案】A [解析] ∵ED是△ABC的中位线,BC=4,∴ED=2.又∵△A′B′C′和△ABC关于点O中心对称,∴E′D′=ED=2.
8. 【答案】C [解析] A1(1,),A2(3,-),A3(5,),A4(7,-),…,
∴点An的坐标为
∵2n+1是奇数,∴点A2n+1的坐标是(4n+1,).故选C.
二、填空题
9. 【答案】4 [解析] ∵王老师、杨老师两家所在的位置关于学校对称,
∴王老师、杨老师两家到学校的距离相等.
∵王老师家距学校2千米,
∴他们两家相距4千米.
故答案为4.
10. 【答案】(3,-1) [解析] 连接各组对应点,其交点坐标即为对称中心点E的坐标.
11. 【答案】(6,-1) [解析] 依题意,得解得∴点A的坐标为(6,-1).
12. 【答案】2 [解析] ∵△ABC绕AC的中点O旋转了180°,
∴OB=OB′,∴BB′=2OB.
又∵OC=OA=AC=1,BC=2,
∴在Rt△OBC中,OB===,
∴BB′=2OB=2 .
13. 【答案】6 [解析] 如图,过点A′作A′B′⊥a,垂足为B′,由题意可知,①与②关于点O中心对称,所以阴影部分的面积可以看作四边形A′B′OD的面积.又A′D⊥b于点D,直线a,b互相垂直,可得四边形A′B′OD是矩形,所以其面积为3×2=6.
14. 【答案】(-1,-1) [解析] 如图,过点A作AD⊥OB于点D.∵△AOB是等腰直角三角形,OB=2,∴OD=AD=1,∴A(1,1),∴点A关于原点对称的点的坐标为(-1,-1).
15. 【答案】5 [解析] ∵点A(x+1,2y+1)与点A′(y-2,x)关于原点O对称,
∴解得
故x2-y2=9-4=5.
故答案为5.
三、作图题
16. 【答案】
解:(1)答案不唯一,画出下列其中一种即可.
(2)答案不唯一,画出下列其中一种即可.
17. 【答案】
解:如图,△A′B′C′即为所求.
四、解答题
18. 【答案】
解:(1)△ABC关于原点O对称的△A1B1C1如图所示.
(2)平移后的△A2B2C2如图所示,其中点B2的坐标为(0,-2),点C2的坐标为(-2,-1).
(3)△A1B1C1 (1,-1)
19. 【答案】
解:(1)如图,△A1B1C1为所作,C1(-1,2).
(2)如图,△A2B2C2为所作,C2(-3,-2).
(3)因为点A的坐标为(2,4),点A3的坐标为(-4,-2),
所以直线l的函数解析式为y=-x.
20. 【答案】
解:(1)如图所示.
(2)?ABA′B′,?BCB′C′,?CA′C′A.
同课章节目录
