人教版 九年级数学 24.3 正多边形和圆 课后训练(Word版 含答案)
文档属性
| 名称 | 人教版 九年级数学 24.3 正多边形和圆 课后训练(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 665.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-15 00:02:15 | ||
图片预览




文档简介
人教版 九年级数学 24.3 正多边形和圆 课后训练
一、选择题
1. 下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形
C.正五边形 D.正六边形
2. 2019·安徽月考 如图,正五边形ABCDE内接于⊙O,过点A作⊙O的切线交对角线DB的延长线于点F,则下列结论不成立的是( )
A.AE∥BF B.AF∥CD
C.DF=AF D.AB=BF
3. 一元硬币的直径约为24 mm,则用它能完全覆盖住的正六边形的边长最大为( )
A.12 mm B.12 mm C.6 mm D.6 mm
4. 如图,边长为3的正五边形ABCDE的顶点A,B在半径为3的圆O上,其他各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆O上时,点C转过的度数为( )
A.12° B.16° C.20° D.24°
5. 如图,将两张完全相同的正六边形纸片(边长为2a)重合在一起,下面一张纸片保持不动,将上面一张纸片沿水平方向向左平移a个单位长度,则空白部分与阴影部分的面积之比是( )
A.5∶2 B.3∶2 C.3∶1 D.2∶1
6. 如图是由7个全等的正六边形组成的网格,正六边形的顶点称为格点,△ABC的顶点都在格点上,设定AB边如图所示,则使△ABC是直角三角形的格点有( )
A.10个 B.8个 C.6个 D.4个
7. 正方形ABCD与正八边形EFGHKLMN的边长相等,初始位置如图所示,将正方形绕点F顺时针旋转使得BC与FG重合,再将正方形绕点G顺时针旋转使得CD与GH重合……按这样的方式将正方形ABCD旋转2020次后,正方形ABCD中与正八边形EFGHKLMN的边重合的边是( )
A.AB B.BC C.CD D.DA
8. 下列用尺规等分圆周的作法正确的有( )
①在圆上依次截取等于半径的弦,就可以六等分圆;②作相互垂直的两条直径,就可以四等分圆;③按①的方法将圆六等分,六个等分点中三个不相邻的点三等分圆;④按②的方法将圆四等分,再平分四条弧,就可以八等分圆.
A.4个 B.3个 C.2个 D.1个
二、填空题
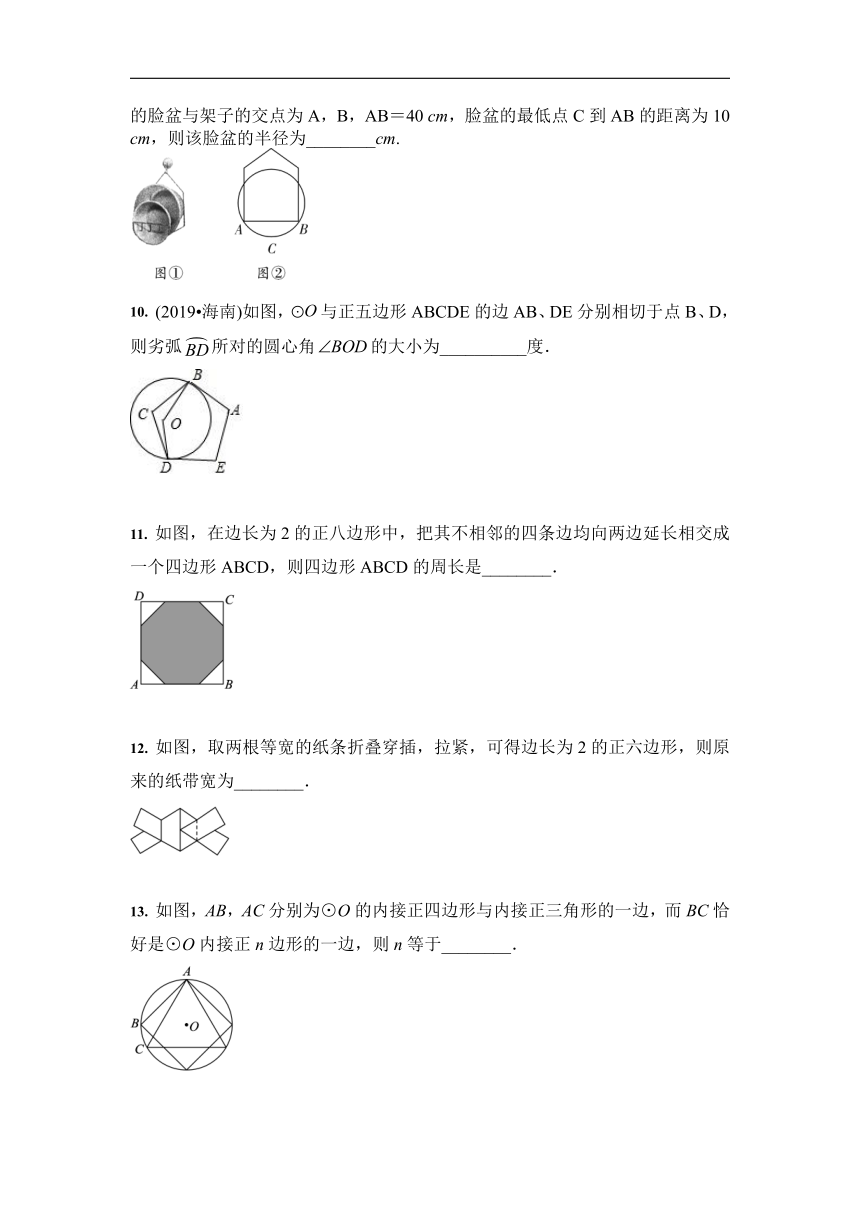
9. 如图①,小敏利用课余时间制作了一个脸盆架,图②是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40 cm,脸盆的最低点C到AB的距离为10 cm,则该脸盆的半径为________cm.
10. (2019?海南)如图,与正五边形ABCDE的边AB、DE分别相切于点B、D,则劣弧所对的圆心角的大小为__________度.
11. 如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是________.
12. 如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形,则原来的纸带宽为________.
13. 如图,AB,AC分别为⊙O的内接正四边形与内接正三角形的一边,而BC恰好是⊙O内接正n边形的一边,则n等于________.
14. 如图为一个半径为4 m的圆形场地,其中放有六个宽为1 m的长方形临时摊位,这些摊位均有两个顶点在场地边上,另两个顶点紧靠相邻摊位的顶点,则每个长方形摊位的长为__________m.
15. 佳佳对科技馆富有创意的科学方舟形象设计很有兴趣,他回家后将一正五边形纸片沿其对称轴对折(如图①所示),旋转放置,做成科学方舟模型(如图②所示).图①中正五边形的边心距OB为,图②中AC为科学方舟船头A到船底的距离,请你计算AC+AB=________.
三、解答题
16. 如图,在正六边形ABCDEF中,点O是中心,AB=10,求这个正六边形的半径、边心距、周长、面积.
17. 如图,P是⊙O上的一点.
(1)在⊙O上求作一点B,使PB是⊙O的内接正三角形的一边;
(2)在上求作一点A,使PA是⊙O的内接正方形的一边;
(3)连接OB,求∠AOB的度数;
(4)求作⊙O的内接正十二边形.
18. 如图,A,B,C,D,E是⊙O上的五等分点,连接AC,CE,EB,BD,DA,得到一个五角星图形和五边形MNFGH.
(1)计算∠CAD的度数;
(2)连接AE,求证:AE=ME.
人教版 九年级数学 24.3 正多边形和圆 课后训练-答案
一、选择题
1. 【答案】A [解析] ∵正三角形一条边所对的圆心角是360°÷3=120°,
正方形一条边所对的圆心角是360°÷4=90°,
正五边形一条边所对的圆心角是360°÷5=72°,
正六边形一条边所对的圆心角是360°÷6=60°,
∴一条边所对的圆心角最大的图形是正三角形.
故选A.
2. 【答案】C
3. 【答案】A [解析] 正六边形外接圆的直径等于正六边形边长的2倍.
4. 【答案】A [解析] 设点E第一次落在圆上时的对应点为E′,连接OA,OB,OE′,如图.
∵五边形ABCDE为正五边形,
∴∠EAB=108°.
∵正五边形ABCDE绕点A逆时针旋转,点E第一次落在圆O上的点E′处,
∴AE′=AE=3.
∵OA=AB=OB=OE′=3,
∴△OAE′,△OAB都为等边三角形,
∴∠OAB=∠OAE′=60°,
∴∠E′AB=120°,
∴∠EAE′=12°,
∴当点E第一次落在圆O上时,点C转过的度数为12°.
5. 【答案】C [解析] 正六边形的面积=6××(2a)2=6 a2,阴影部分的面积=a·2 a=2 a2,
∴空白部分与阴影部分的面积之比是=6 a2∶2 a2=3∶1.
6. 【答案】A [解析] 如图,当AB是直角边时,点C共有6个位置,即有6个直角三角形;当AB是斜边时,点C共有4个位置,即有4个直角三角形.
综上所述,使△ABC是直角三角形的格点有6+4=10(个).故选A.
7. 【答案】A [解析] 由题意可得正方形每旋转8次则回到原来的位置.
∵2020÷8=252……4,
∴正方形ABCD旋转2020次后,AB与正八边形EFGHKLMN的边重合.
8. 【答案】A
二、填空题
9. 【答案】25 【解析】 如解图,取圆心为O,连接OA、OC,OC交AB于点D,则OC⊥AB.设⊙O 的半径为r,则OA=OC=r,又∵CD=10,∴OD=r-10,∵AB=40,OC⊥AB,∴AD=20.在Rt△ADO中,由勾股定理得:r2=202+(r-10)2,解得r=25,即脸盆的半径为25 cm.
10. 【答案】144
【解析】五边形ABCDE是正五边形,∴.
∵AB、DE与相切,∴,
∴,故答案为:144.
11. 【答案】8+8 [解析] 易证四边形ABCD是正方形.
由题意可得AD=2+×2=2+2 ,
∴四边形ABCD的周长是4×(2+2 )=8+8 .
故答案为8+8 .
12. 【答案】 [解析] 边长为2的正六边形由6个边长为2的等边三角形组成,其中等边三角形的高为原来的纸带宽度,所以原来的纸带宽度为.
13. 【答案】12 [解析] 连接OA,OB,OC,如图.
∵AB,AC分别为⊙O的内接正四边形与内接正三角形的一边,
∴∠AOB=90°,∠AOC=120°,
∴∠BOC=∠AOC-∠AOB=30°,∴n==12,即BC恰好是⊙O内接正十二边形的一边.
14. 【答案】 [解析] 设圆心是O,连接OA,OB,过点O作OC⊥BC于点C,交AD于点D.设长方形摊位的长是2x m.在Rt△OAD中,∠AOD=30°,AD=x m,则OD=x m.
在Rt△OBC中,由勾股定理,得OC= m.
∵OC-OD=CD=1 m,
∴=x+1,
解得x=(负值已舍去),
则2x=,
∴长方形摊位的长为 m.
15. 【答案】 [解析] 如图①,连接OF,OE.
由题意,知AB⊥EF,则S正五边形AGFED=5×S△OEF=5×(EF·OB)=2.5×EF=5 BE.
如图②,连接AE.
S正五边形AGFED=2×S四边形ABED=2×(S△ABE+S△ADE)=2×(AB·BE+DE·AC)=AB·BE+DE·AC=AB·BE+2BE·AC=BE·(AB+2AC),∴5 BE=BE·(AB+2AC).
∴AB+2AC=5 ,∴AC+AB= .
三、解答题
16. 【答案】
解:连接OB,OC,过点O作OH⊥BC于点H.∵正六边形的中心角为=60°,OB=OC,∴△OBC是等边三角形,
∴半径R=OB=BC=AB=10.∵OH⊥BC,∴∠BOH=30°,∴BH=OB=5.
在Rt△OBH中,边心距r=OH==5 ,周长l=6AB=6×10=60.
∵S△OBC=BC·OH=×10×5 =25 ,
∴正六边形的面积S=6S△OBC=6×25 =150 .
17. 【答案】
解:(1)如图①,以点P为圆心,OP长为半径画圆弧交⊙O于点M,再以点M为圆心,OM长为半径画圆弧交⊙O于点B,连接PB,则PB即为所求.
(2)如图①,作直径PH,再过圆心作直径PH的垂线交于点A,连接PA,则PA即为所求.
(3)∵PA是⊙O的内接正方形的一边,
∴∠AOP=90°.
∵PB是⊙O的内接正三角形的一边,
∴∠BOP=120°,∴∠AOB=30°.
(4)如图②,以点P为圆心,OP长为半径在⊙O上依次截取5个点,这5个点连同点P是⊙O的六等分点,再作各弧的中点,顺次连接12个点,得到⊙O的内接正十二边形.
18. 【答案】
解:(1)∵A,B,C,D,E是⊙O上的五等分点,
∴∠COD==72°,
∴∠CAD=∠COD=36°.
(2)证明:∵A,B,C,D,E是⊙O上的五等分点,∴====,
∴∠DAE=∠AEB=∠CAD=36°,
∴∠MAE=72°,
∴∠AME=180°-∠MAE-∠AEB=72°=∠MAE,∴AE=ME.
一、选择题
1. 下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形
C.正五边形 D.正六边形
2. 2019·安徽月考 如图,正五边形ABCDE内接于⊙O,过点A作⊙O的切线交对角线DB的延长线于点F,则下列结论不成立的是( )
A.AE∥BF B.AF∥CD
C.DF=AF D.AB=BF
3. 一元硬币的直径约为24 mm,则用它能完全覆盖住的正六边形的边长最大为( )
A.12 mm B.12 mm C.6 mm D.6 mm
4. 如图,边长为3的正五边形ABCDE的顶点A,B在半径为3的圆O上,其他各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆O上时,点C转过的度数为( )
A.12° B.16° C.20° D.24°
5. 如图,将两张完全相同的正六边形纸片(边长为2a)重合在一起,下面一张纸片保持不动,将上面一张纸片沿水平方向向左平移a个单位长度,则空白部分与阴影部分的面积之比是( )
A.5∶2 B.3∶2 C.3∶1 D.2∶1
6. 如图是由7个全等的正六边形组成的网格,正六边形的顶点称为格点,△ABC的顶点都在格点上,设定AB边如图所示,则使△ABC是直角三角形的格点有( )
A.10个 B.8个 C.6个 D.4个
7. 正方形ABCD与正八边形EFGHKLMN的边长相等,初始位置如图所示,将正方形绕点F顺时针旋转使得BC与FG重合,再将正方形绕点G顺时针旋转使得CD与GH重合……按这样的方式将正方形ABCD旋转2020次后,正方形ABCD中与正八边形EFGHKLMN的边重合的边是( )
A.AB B.BC C.CD D.DA
8. 下列用尺规等分圆周的作法正确的有( )
①在圆上依次截取等于半径的弦,就可以六等分圆;②作相互垂直的两条直径,就可以四等分圆;③按①的方法将圆六等分,六个等分点中三个不相邻的点三等分圆;④按②的方法将圆四等分,再平分四条弧,就可以八等分圆.
A.4个 B.3个 C.2个 D.1个
二、填空题
9. 如图①,小敏利用课余时间制作了一个脸盆架,图②是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40 cm,脸盆的最低点C到AB的距离为10 cm,则该脸盆的半径为________cm.
10. (2019?海南)如图,与正五边形ABCDE的边AB、DE分别相切于点B、D,则劣弧所对的圆心角的大小为__________度.
11. 如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是________.
12. 如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形,则原来的纸带宽为________.
13. 如图,AB,AC分别为⊙O的内接正四边形与内接正三角形的一边,而BC恰好是⊙O内接正n边形的一边,则n等于________.
14. 如图为一个半径为4 m的圆形场地,其中放有六个宽为1 m的长方形临时摊位,这些摊位均有两个顶点在场地边上,另两个顶点紧靠相邻摊位的顶点,则每个长方形摊位的长为__________m.
15. 佳佳对科技馆富有创意的科学方舟形象设计很有兴趣,他回家后将一正五边形纸片沿其对称轴对折(如图①所示),旋转放置,做成科学方舟模型(如图②所示).图①中正五边形的边心距OB为,图②中AC为科学方舟船头A到船底的距离,请你计算AC+AB=________.
三、解答题
16. 如图,在正六边形ABCDEF中,点O是中心,AB=10,求这个正六边形的半径、边心距、周长、面积.
17. 如图,P是⊙O上的一点.
(1)在⊙O上求作一点B,使PB是⊙O的内接正三角形的一边;
(2)在上求作一点A,使PA是⊙O的内接正方形的一边;
(3)连接OB,求∠AOB的度数;
(4)求作⊙O的内接正十二边形.
18. 如图,A,B,C,D,E是⊙O上的五等分点,连接AC,CE,EB,BD,DA,得到一个五角星图形和五边形MNFGH.
(1)计算∠CAD的度数;
(2)连接AE,求证:AE=ME.
人教版 九年级数学 24.3 正多边形和圆 课后训练-答案
一、选择题
1. 【答案】A [解析] ∵正三角形一条边所对的圆心角是360°÷3=120°,
正方形一条边所对的圆心角是360°÷4=90°,
正五边形一条边所对的圆心角是360°÷5=72°,
正六边形一条边所对的圆心角是360°÷6=60°,
∴一条边所对的圆心角最大的图形是正三角形.
故选A.
2. 【答案】C
3. 【答案】A [解析] 正六边形外接圆的直径等于正六边形边长的2倍.
4. 【答案】A [解析] 设点E第一次落在圆上时的对应点为E′,连接OA,OB,OE′,如图.
∵五边形ABCDE为正五边形,
∴∠EAB=108°.
∵正五边形ABCDE绕点A逆时针旋转,点E第一次落在圆O上的点E′处,
∴AE′=AE=3.
∵OA=AB=OB=OE′=3,
∴△OAE′,△OAB都为等边三角形,
∴∠OAB=∠OAE′=60°,
∴∠E′AB=120°,
∴∠EAE′=12°,
∴当点E第一次落在圆O上时,点C转过的度数为12°.
5. 【答案】C [解析] 正六边形的面积=6××(2a)2=6 a2,阴影部分的面积=a·2 a=2 a2,
∴空白部分与阴影部分的面积之比是=6 a2∶2 a2=3∶1.
6. 【答案】A [解析] 如图,当AB是直角边时,点C共有6个位置,即有6个直角三角形;当AB是斜边时,点C共有4个位置,即有4个直角三角形.
综上所述,使△ABC是直角三角形的格点有6+4=10(个).故选A.
7. 【答案】A [解析] 由题意可得正方形每旋转8次则回到原来的位置.
∵2020÷8=252……4,
∴正方形ABCD旋转2020次后,AB与正八边形EFGHKLMN的边重合.
8. 【答案】A
二、填空题
9. 【答案】25 【解析】 如解图,取圆心为O,连接OA、OC,OC交AB于点D,则OC⊥AB.设⊙O 的半径为r,则OA=OC=r,又∵CD=10,∴OD=r-10,∵AB=40,OC⊥AB,∴AD=20.在Rt△ADO中,由勾股定理得:r2=202+(r-10)2,解得r=25,即脸盆的半径为25 cm.
10. 【答案】144
【解析】五边形ABCDE是正五边形,∴.
∵AB、DE与相切,∴,
∴,故答案为:144.
11. 【答案】8+8 [解析] 易证四边形ABCD是正方形.
由题意可得AD=2+×2=2+2 ,
∴四边形ABCD的周长是4×(2+2 )=8+8 .
故答案为8+8 .
12. 【答案】 [解析] 边长为2的正六边形由6个边长为2的等边三角形组成,其中等边三角形的高为原来的纸带宽度,所以原来的纸带宽度为.
13. 【答案】12 [解析] 连接OA,OB,OC,如图.
∵AB,AC分别为⊙O的内接正四边形与内接正三角形的一边,
∴∠AOB=90°,∠AOC=120°,
∴∠BOC=∠AOC-∠AOB=30°,∴n==12,即BC恰好是⊙O内接正十二边形的一边.
14. 【答案】 [解析] 设圆心是O,连接OA,OB,过点O作OC⊥BC于点C,交AD于点D.设长方形摊位的长是2x m.在Rt△OAD中,∠AOD=30°,AD=x m,则OD=x m.
在Rt△OBC中,由勾股定理,得OC= m.
∵OC-OD=CD=1 m,
∴=x+1,
解得x=(负值已舍去),
则2x=,
∴长方形摊位的长为 m.
15. 【答案】 [解析] 如图①,连接OF,OE.
由题意,知AB⊥EF,则S正五边形AGFED=5×S△OEF=5×(EF·OB)=2.5×EF=5 BE.
如图②,连接AE.
S正五边形AGFED=2×S四边形ABED=2×(S△ABE+S△ADE)=2×(AB·BE+DE·AC)=AB·BE+DE·AC=AB·BE+2BE·AC=BE·(AB+2AC),∴5 BE=BE·(AB+2AC).
∴AB+2AC=5 ,∴AC+AB= .
三、解答题
16. 【答案】
解:连接OB,OC,过点O作OH⊥BC于点H.∵正六边形的中心角为=60°,OB=OC,∴△OBC是等边三角形,
∴半径R=OB=BC=AB=10.∵OH⊥BC,∴∠BOH=30°,∴BH=OB=5.
在Rt△OBH中,边心距r=OH==5 ,周长l=6AB=6×10=60.
∵S△OBC=BC·OH=×10×5 =25 ,
∴正六边形的面积S=6S△OBC=6×25 =150 .
17. 【答案】
解:(1)如图①,以点P为圆心,OP长为半径画圆弧交⊙O于点M,再以点M为圆心,OM长为半径画圆弧交⊙O于点B,连接PB,则PB即为所求.
(2)如图①,作直径PH,再过圆心作直径PH的垂线交于点A,连接PA,则PA即为所求.
(3)∵PA是⊙O的内接正方形的一边,
∴∠AOP=90°.
∵PB是⊙O的内接正三角形的一边,
∴∠BOP=120°,∴∠AOB=30°.
(4)如图②,以点P为圆心,OP长为半径在⊙O上依次截取5个点,这5个点连同点P是⊙O的六等分点,再作各弧的中点,顺次连接12个点,得到⊙O的内接正十二边形.
18. 【答案】
解:(1)∵A,B,C,D,E是⊙O上的五等分点,
∴∠COD==72°,
∴∠CAD=∠COD=36°.
(2)证明:∵A,B,C,D,E是⊙O上的五等分点,∴====,
∴∠DAE=∠AEB=∠CAD=36°,
∴∠MAE=72°,
∴∠AME=180°-∠MAE-∠AEB=72°=∠MAE,∴AE=ME.
同课章节目录
