人教版 九年级数学上册 24.2 点和圆、直线和圆的位置关系 同步训练(Word版 含答案)
文档属性
| 名称 | 人教版 九年级数学上册 24.2 点和圆、直线和圆的位置关系 同步训练(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 488.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-15 00:08:27 | ||
图片预览




文档简介
人教版 九年级数学上册 24.2 点和圆、直线和圆的位置关系 同步训练
一、选择题
1. 下列说法中,正确的是( )
A.垂直于半径的直线是圆的切线
B.经过半径的外端且垂直于这条半径的直线是圆的切线
C.经过半径的端点且垂直于这条半径的直线是圆的切线
D.到圆心的距离等于直径的直线是圆的切线
2. (2019?益阳)如图,PA、PB为圆O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是
A.PA=PB B.∠BPD=∠APDC.AB⊥PD D.AB平分PD
3. 平面上⊙O与四条直线l1,l2,l3,l4的位置关系如图.若⊙O的半径为2 cm,且点O到其中一条直线的距离为2.2 cm,则这条直线是( )
A.ll B.l2 C.l3 D.l4
4. 在Rt△ABC中,∠C=90°,BC=3 cm,AC=4 cm,以点C为圆心,以2.5 cm为半径画圆,则⊙C与直线AB的位置关系是( )
A. 相交 B. 相切 C. 相离 D. 不能确定
5. 如图,一个边长为4 cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为( )
A.4 cm B.3 cm C.2 cm D.1.5 cm
6. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )
A. 1<r<4
B. 2<r<4
C. 1<r<8
D. 2<r<8
7. 2020·武汉模拟 在平面直角坐标系中,圆心为坐标原点,⊙O的半径为10,则P(-10,1)与⊙O的位置关系为( )
A.点P在⊙O上 B.点P在⊙O外
C.点P在⊙O内 D.无法确定
8. 如图0,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
图0
A. B.2 C. D.
二、填空题
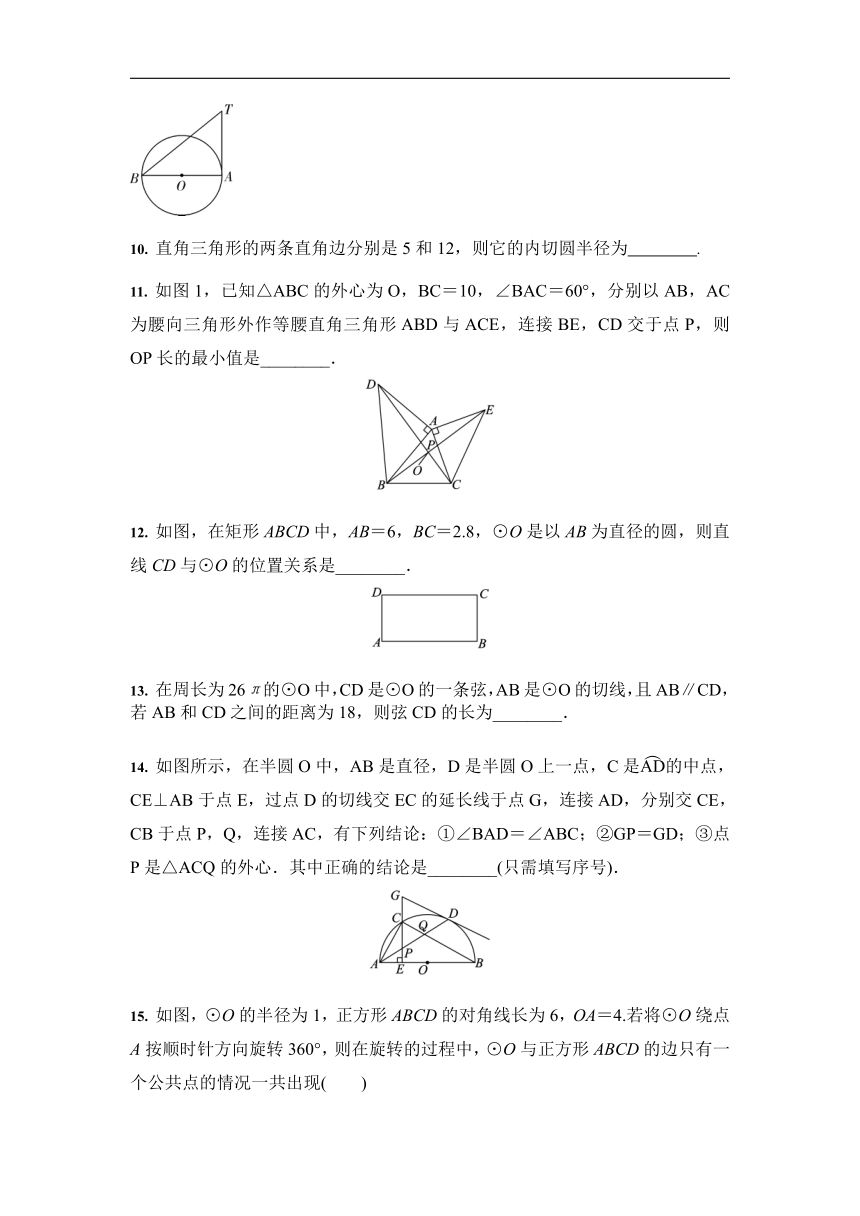
9. 如图,AT切⊙O于点A,AB是⊙O的直径.若∠ABT=40°,则∠ATB=________.
10. 直角三角形的两条直角边分别是5和12,则它的内切圆半径为 .?
11. 如图1,已知△ABC的外心为O,BC=10,∠BAC=60°,分别以AB,AC为腰向三角形外作等腰直角三角形ABD与ACE,连接BE,CD交于点P,则OP长的最小值是________.
12. 如图,在矩形ABCD中,AB=6,BC=2.8,⊙O是以AB为直径的圆,则直线CD与⊙O的位置关系是________.
13. 在周长为26π的⊙O中,CD是⊙O的一条弦,AB是⊙O的切线,且AB∥CD,若AB和CD之间的距离为18,则弦CD的长为________.
14. 如图所示,在半圆O中,AB是直径,D是半圆O上一点,C是的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,有下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心.其中正确的结论是________(只需填写序号).
15. 如图,⊙O的半径为1,正方形ABCD的对角线长为6,OA=4.若将⊙O绕点A按顺时针方向旋转360°,则在旋转的过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现( )
A.3次 B.4次 C.5次 D.6次
16. 2019·兴化期中 已知等边三角形ABC的边长为2,D为BC的中点,连接AD.点O在线段AD上运动(不与端点A,D重合),以点O为圆心,为半径作圆,当⊙O与△ABC的边有且只有两个公共点时,DO的取值范围为________.
三、解答题
17. 如图,MP切⊙O于点M,直线PO交⊙O于点A、B,弦AC∥MP,求证:MO∥BC.
18. 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,P是CD的延长线上一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若PD=,求⊙O的直径.
19. 在△ABC中,AB=AC=10,BC=16,⊙A的半径为7,判断⊙A与直线BC的位置关系,并说明理由.
20. 2019·天津 如图,已知PA,PB分别与⊙O相切于点A,B,∠APB=80°,C为⊙O上一点.
(1)如图①,求∠ACB的大小;
(2)如图②,AE为⊙O的直径,AE与BC相交于点D.若AB=AD,求∠EAC的大小.
21. 如图,在平面直角坐标系中,以点O为圆心,5个单位长度为半径画圆.直线MN经过x轴上的一动点P(m,0)且垂直于x轴,当点P在x轴上移动时,直线MN也随之平行移动.按下列条件求m的值或取值范围.
(1)⊙O上任何一点到直线MN的距离都不等于3;
(2)⊙O上有且只有一点到直线MN的距离等于3;
(3)⊙O上有且只有两点到直线MN的距离等于3;
(4)随着m的变化,⊙O上到直线MN的距离等于3的点的个数还有哪些变化?请说明所有各种情形及对应m的值或取值范围.
人教版 九年级数学上册 24.2 点和圆、直线和圆的位置关系 同步训练-答案
一、选择题
1. 【答案】B
2. 【答案】D
【解析】∵PA,PB是⊙O的切线,∴PA=PB,所以A成立;∠BPD=∠APD,所以B成立;
∴AB⊥PD,所以C成立;
∵PA,PB是⊙O的切线,∴AB⊥PD,且AC=BC,
只有当AD∥PB,BD∥PA时,AB平分PD,所以D不一定成立,故选D.
3. 【答案】C [解析] 因为所求直线到圆心O的距离为2.2 cm>半径2 cm,所以此直线与⊙O相离,所以这条直线为直线l3.
4. 【答案】 A 【解析】如解图,在Rt△ABC中,AC=4,BC=3,由勾股定理得AB=5.过C作CD⊥AB于D,则S△ABC=AC·BC=AB·CD,解得CD=2.4<2.5,∴直线AB与⊙C相交.
解图
5. 【答案】B [解析] 如图,连接OC,并过点O作OF⊥CE于点F.
∵△ABC为等边三角形,边长为4 cm,
∴△ABC的高为2 cm,∴OC= cm.
又∵⊙O与BC相切于点C,∠ACB=60°,
∴∠OCF=30°.
在Rt△OFC中,可得FC= cm,
∴CE=2FC=3 cm.
6. 【答案】B 【解析】连接AD,则AD===5,∵⊙A与⊙D相交,∴3-r<5<3+r,解得2<r<8,又∵点B在⊙D外,∴r 解图
7. 【答案】B
8. 【答案】B [解析] ∵∠ABC=90°,
∴∠ABP+∠PBC=90°.
∵∠PAB=∠PBC,
∴∠ABP+∠PAB=90°,∴∠APB=90°,
∴点P在以AB为直径的圆上,设圆心为O,连接OC交⊙O于点P,此时CP最小.
在Rt△BCO中,∵∠OBC=90°,BC=4,OB=3,
∴OC=5,OP=OB=3,∴PC=OC-OP=5-3=2,∴PC的最小值为2.
二、填空题
9. 【答案】50° 【解析】∵AT是⊙O的切线,AB是⊙O的直径,∴∠BAT=90°,在Rt△BAT中,∵∠ABT=40°,∴∠ATB=50°.
10. 【答案】2 [解析]直角三角形的斜边==13,所以它的内切圆半径==2.
11. 【答案】5- [解析] ∵∠BAD=∠CAE=90°,
∴∠DAC=∠BAE.
在△DAC和△BAE中,
∴△DAC≌△BAE(SAS),
∴∠ADC=∠ABE,
从而∠PDB+∠PBD=90°,
即∠DPB=90°,从而∠BPC=90°,
∴点P在以BC为直径的圆上.
如图,过点O作OH⊥BC于点H,连接OB,OC.
∵△ABC的外心为O,∠BAC=60°,
∴∠BOC=120°.又∵BC=10,
∴OH= ,∴OP长的最小值是5- .
12. 【答案】相交 [解析] 设AB的中点为O,则点O到CD的距离为2.8.因为⊙O的半径为3,3>2.8,所以直线CD与⊙O的位置关系是相交.
13. 【答案】24 【解析】设AB切⊙O于点E,如解图,连接EO并延长交CD于点M,∵C⊙O=26π=2πr,∴r=13,∵AB∥CD,且AB与CD之间的距离为18,∴OM=18-r=5,∵AB为⊙O的切线,∴∠CMO=∠AEO=90°,∴在Rt△CMO中,CM==12,∴CD=2CM=24.
解图
14. 【答案】②③ [解析] ∵在半圆O中,AB是直径,D是半圆O上一点,C是的中点,
∴=,但不一定等于,
∴∠BAD与∠ABC不一定相等,故①错误.
如图,连接OD,则OD⊥GD,∠OAD=∠ODA.
∵∠ODA+∠GDP=90°,∠OAD+∠GPD=∠OAD+∠APE=90°,
∴∠GPD=∠GDP,∴GP=GD,故②正确.
补全⊙O,延长CE交⊙O于点F.
∵CE⊥AB,∴A为的中点,即=.
又∵C为的中点,∴=,∴=,
∴∠CAP=∠ACP,∴AP=CP.
∵AB为⊙O的直径,∴∠ACQ=90°,
∴∠ACP+∠PCQ=90°,∠CAP+∠PQC=90°,
∴∠PCQ=∠PQC,∴PC=PQ,
∴AP=PQ,即P为Rt△ACQ的斜边AQ的中点,
∴点P为Rt△ACQ的外心,故③正确.
15. 【答案】B [解析] ∵正方形ABCD的对角线长为6,∴它的边长为3 .
如图,⊙O与正方形ABCD的边AB,AD只有一个公共点的情况各有1次,与边BC,CD只有一个公共点的情况各有1次,
∴在旋转的过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现4次.
16. 【答案】0∴AD⊥BC,BD=1,AD=.
分四种情况讨论:
(1)如图①所示,当0⊙O与△ABC的BC边有且只有两个公共点,
(2)如图②所示,当DO=时,
⊙O与△ABC的边有三个公共点;
(3)如图③所示,当⊙O经过△ABC的顶点A时,⊙O与△ABC的边有三个公共点,则当(4)如图④所示,当综上,当0故答案为0三、解答题
17. 【答案】
证明:∵AB是⊙O的直径,∴∠ACB=90°,∵MP为⊙O的切线,
∴∠PMO=90°,∵MP∥AC,∴∠P=∠CAB,
∴∠MOP=∠B,
故MO∥BC.
18. 【答案】
解:(1)证明:如图,连接OA.
∵∠B=60°,
∴∠AOC=2∠B=120°.
又∵OA=OC,
∴∠OAC=∠OCA=30°.
又∵AP=AC,
∴∠P=∠OCA=30°,
∴∠OAP=∠AOC-∠P=90°,
∴OA⊥PA.
又∵OA是⊙O的半径,
∴PA是⊙O的切线.
(2)在Rt△OAP中,
∵∠P=30°,
∴PO=2OA=OD+PD.
又∵OA=OD,
∴PD=OD=OA.
∵PD=,
∴2OA=2PD=2 ,
∴⊙O的直径为2 .
19. 【答案】
解:⊙A与直线BC相交.
理由:过点A作AD⊥BC于点D,
则BD=CD=8.
∵AB=AC=10,
∴AD=6.
∵6<7,
∴⊙A与直线BC相交.
20. 【答案】
解:(1)如图①,连接OA,OB,
∵PA,PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
∴∠AOB=360°-90°-90°-80°=100°.
由圆周角定理,得∠ACB=∠AOB=50°.
(2)如图②,连接CE.
∵AE为⊙O的直径,
∴∠ACE=90°.
∵∠ACB=50°,
∴∠BCE=90°-50°=40°,
∴∠BAE=∠BCE=40°.
∵AB=AD,
∴∠ABD=∠ADB=70°,
∴∠EAC=∠ADB-∠ACB=20°.
21. 【答案】
解:(1)m<-8或m>8
(2)m=-8或m=8
(3)-8<m<-2或2<m<8
(4)当m=-2或m=2时,⊙O上有且只有三个点到直线MN的距离等于3;
当-2<m<2时,⊙O上有且只有四个点到直线MN的距离等于3.
一、选择题
1. 下列说法中,正确的是( )
A.垂直于半径的直线是圆的切线
B.经过半径的外端且垂直于这条半径的直线是圆的切线
C.经过半径的端点且垂直于这条半径的直线是圆的切线
D.到圆心的距离等于直径的直线是圆的切线
2. (2019?益阳)如图,PA、PB为圆O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是
A.PA=PB B.∠BPD=∠APDC.AB⊥PD D.AB平分PD
3. 平面上⊙O与四条直线l1,l2,l3,l4的位置关系如图.若⊙O的半径为2 cm,且点O到其中一条直线的距离为2.2 cm,则这条直线是( )
A.ll B.l2 C.l3 D.l4
4. 在Rt△ABC中,∠C=90°,BC=3 cm,AC=4 cm,以点C为圆心,以2.5 cm为半径画圆,则⊙C与直线AB的位置关系是( )
A. 相交 B. 相切 C. 相离 D. 不能确定
5. 如图,一个边长为4 cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为( )
A.4 cm B.3 cm C.2 cm D.1.5 cm
6. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )
A. 1<r<4
B. 2<r<4
C. 1<r<8
D. 2<r<8
7. 2020·武汉模拟 在平面直角坐标系中,圆心为坐标原点,⊙O的半径为10,则P(-10,1)与⊙O的位置关系为( )
A.点P在⊙O上 B.点P在⊙O外
C.点P在⊙O内 D.无法确定
8. 如图0,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
图0
A. B.2 C. D.
二、填空题
9. 如图,AT切⊙O于点A,AB是⊙O的直径.若∠ABT=40°,则∠ATB=________.
10. 直角三角形的两条直角边分别是5和12,则它的内切圆半径为 .?
11. 如图1,已知△ABC的外心为O,BC=10,∠BAC=60°,分别以AB,AC为腰向三角形外作等腰直角三角形ABD与ACE,连接BE,CD交于点P,则OP长的最小值是________.
12. 如图,在矩形ABCD中,AB=6,BC=2.8,⊙O是以AB为直径的圆,则直线CD与⊙O的位置关系是________.
13. 在周长为26π的⊙O中,CD是⊙O的一条弦,AB是⊙O的切线,且AB∥CD,若AB和CD之间的距离为18,则弦CD的长为________.
14. 如图所示,在半圆O中,AB是直径,D是半圆O上一点,C是的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,有下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心.其中正确的结论是________(只需填写序号).
15. 如图,⊙O的半径为1,正方形ABCD的对角线长为6,OA=4.若将⊙O绕点A按顺时针方向旋转360°,则在旋转的过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现( )
A.3次 B.4次 C.5次 D.6次
16. 2019·兴化期中 已知等边三角形ABC的边长为2,D为BC的中点,连接AD.点O在线段AD上运动(不与端点A,D重合),以点O为圆心,为半径作圆,当⊙O与△ABC的边有且只有两个公共点时,DO的取值范围为________.
三、解答题
17. 如图,MP切⊙O于点M,直线PO交⊙O于点A、B,弦AC∥MP,求证:MO∥BC.
18. 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,P是CD的延长线上一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若PD=,求⊙O的直径.
19. 在△ABC中,AB=AC=10,BC=16,⊙A的半径为7,判断⊙A与直线BC的位置关系,并说明理由.
20. 2019·天津 如图,已知PA,PB分别与⊙O相切于点A,B,∠APB=80°,C为⊙O上一点.
(1)如图①,求∠ACB的大小;
(2)如图②,AE为⊙O的直径,AE与BC相交于点D.若AB=AD,求∠EAC的大小.
21. 如图,在平面直角坐标系中,以点O为圆心,5个单位长度为半径画圆.直线MN经过x轴上的一动点P(m,0)且垂直于x轴,当点P在x轴上移动时,直线MN也随之平行移动.按下列条件求m的值或取值范围.
(1)⊙O上任何一点到直线MN的距离都不等于3;
(2)⊙O上有且只有一点到直线MN的距离等于3;
(3)⊙O上有且只有两点到直线MN的距离等于3;
(4)随着m的变化,⊙O上到直线MN的距离等于3的点的个数还有哪些变化?请说明所有各种情形及对应m的值或取值范围.
人教版 九年级数学上册 24.2 点和圆、直线和圆的位置关系 同步训练-答案
一、选择题
1. 【答案】B
2. 【答案】D
【解析】∵PA,PB是⊙O的切线,∴PA=PB,所以A成立;∠BPD=∠APD,所以B成立;
∴AB⊥PD,所以C成立;
∵PA,PB是⊙O的切线,∴AB⊥PD,且AC=BC,
只有当AD∥PB,BD∥PA时,AB平分PD,所以D不一定成立,故选D.
3. 【答案】C [解析] 因为所求直线到圆心O的距离为2.2 cm>半径2 cm,所以此直线与⊙O相离,所以这条直线为直线l3.
4. 【答案】 A 【解析】如解图,在Rt△ABC中,AC=4,BC=3,由勾股定理得AB=5.过C作CD⊥AB于D,则S△ABC=AC·BC=AB·CD,解得CD=2.4<2.5,∴直线AB与⊙C相交.
解图
5. 【答案】B [解析] 如图,连接OC,并过点O作OF⊥CE于点F.
∵△ABC为等边三角形,边长为4 cm,
∴△ABC的高为2 cm,∴OC= cm.
又∵⊙O与BC相切于点C,∠ACB=60°,
∴∠OCF=30°.
在Rt△OFC中,可得FC= cm,
∴CE=2FC=3 cm.
6. 【答案】B 【解析】连接AD,则AD===5,∵⊙A与⊙D相交,∴3-r<5<3+r,解得2<r<8,又∵点B在⊙D外,∴r
7. 【答案】B
8. 【答案】B [解析] ∵∠ABC=90°,
∴∠ABP+∠PBC=90°.
∵∠PAB=∠PBC,
∴∠ABP+∠PAB=90°,∴∠APB=90°,
∴点P在以AB为直径的圆上,设圆心为O,连接OC交⊙O于点P,此时CP最小.
在Rt△BCO中,∵∠OBC=90°,BC=4,OB=3,
∴OC=5,OP=OB=3,∴PC=OC-OP=5-3=2,∴PC的最小值为2.
二、填空题
9. 【答案】50° 【解析】∵AT是⊙O的切线,AB是⊙O的直径,∴∠BAT=90°,在Rt△BAT中,∵∠ABT=40°,∴∠ATB=50°.
10. 【答案】2 [解析]直角三角形的斜边==13,所以它的内切圆半径==2.
11. 【答案】5- [解析] ∵∠BAD=∠CAE=90°,
∴∠DAC=∠BAE.
在△DAC和△BAE中,
∴△DAC≌△BAE(SAS),
∴∠ADC=∠ABE,
从而∠PDB+∠PBD=90°,
即∠DPB=90°,从而∠BPC=90°,
∴点P在以BC为直径的圆上.
如图,过点O作OH⊥BC于点H,连接OB,OC.
∵△ABC的外心为O,∠BAC=60°,
∴∠BOC=120°.又∵BC=10,
∴OH= ,∴OP长的最小值是5- .
12. 【答案】相交 [解析] 设AB的中点为O,则点O到CD的距离为2.8.因为⊙O的半径为3,3>2.8,所以直线CD与⊙O的位置关系是相交.
13. 【答案】24 【解析】设AB切⊙O于点E,如解图,连接EO并延长交CD于点M,∵C⊙O=26π=2πr,∴r=13,∵AB∥CD,且AB与CD之间的距离为18,∴OM=18-r=5,∵AB为⊙O的切线,∴∠CMO=∠AEO=90°,∴在Rt△CMO中,CM==12,∴CD=2CM=24.
解图
14. 【答案】②③ [解析] ∵在半圆O中,AB是直径,D是半圆O上一点,C是的中点,
∴=,但不一定等于,
∴∠BAD与∠ABC不一定相等,故①错误.
如图,连接OD,则OD⊥GD,∠OAD=∠ODA.
∵∠ODA+∠GDP=90°,∠OAD+∠GPD=∠OAD+∠APE=90°,
∴∠GPD=∠GDP,∴GP=GD,故②正确.
补全⊙O,延长CE交⊙O于点F.
∵CE⊥AB,∴A为的中点,即=.
又∵C为的中点,∴=,∴=,
∴∠CAP=∠ACP,∴AP=CP.
∵AB为⊙O的直径,∴∠ACQ=90°,
∴∠ACP+∠PCQ=90°,∠CAP+∠PQC=90°,
∴∠PCQ=∠PQC,∴PC=PQ,
∴AP=PQ,即P为Rt△ACQ的斜边AQ的中点,
∴点P为Rt△ACQ的外心,故③正确.
15. 【答案】B [解析] ∵正方形ABCD的对角线长为6,∴它的边长为3 .
如图,⊙O与正方形ABCD的边AB,AD只有一个公共点的情况各有1次,与边BC,CD只有一个公共点的情况各有1次,
∴在旋转的过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现4次.
16. 【答案】0
分四种情况讨论:
(1)如图①所示,当0
(2)如图②所示,当DO=时,
⊙O与△ABC的边有三个公共点;
(3)如图③所示,当⊙O经过△ABC的顶点A时,⊙O与△ABC的边有三个公共点,则当
17. 【答案】
证明:∵AB是⊙O的直径,∴∠ACB=90°,∵MP为⊙O的切线,
∴∠PMO=90°,∵MP∥AC,∴∠P=∠CAB,
∴∠MOP=∠B,
故MO∥BC.
18. 【答案】
解:(1)证明:如图,连接OA.
∵∠B=60°,
∴∠AOC=2∠B=120°.
又∵OA=OC,
∴∠OAC=∠OCA=30°.
又∵AP=AC,
∴∠P=∠OCA=30°,
∴∠OAP=∠AOC-∠P=90°,
∴OA⊥PA.
又∵OA是⊙O的半径,
∴PA是⊙O的切线.
(2)在Rt△OAP中,
∵∠P=30°,
∴PO=2OA=OD+PD.
又∵OA=OD,
∴PD=OD=OA.
∵PD=,
∴2OA=2PD=2 ,
∴⊙O的直径为2 .
19. 【答案】
解:⊙A与直线BC相交.
理由:过点A作AD⊥BC于点D,
则BD=CD=8.
∵AB=AC=10,
∴AD=6.
∵6<7,
∴⊙A与直线BC相交.
20. 【答案】
解:(1)如图①,连接OA,OB,
∵PA,PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
∴∠AOB=360°-90°-90°-80°=100°.
由圆周角定理,得∠ACB=∠AOB=50°.
(2)如图②,连接CE.
∵AE为⊙O的直径,
∴∠ACE=90°.
∵∠ACB=50°,
∴∠BCE=90°-50°=40°,
∴∠BAE=∠BCE=40°.
∵AB=AD,
∴∠ABD=∠ADB=70°,
∴∠EAC=∠ADB-∠ACB=20°.
21. 【答案】
解:(1)m<-8或m>8
(2)m=-8或m=8
(3)-8<m<-2或2<m<8
(4)当m=-2或m=2时,⊙O上有且只有三个点到直线MN的距离等于3;
当-2<m<2时,⊙O上有且只有四个点到直线MN的距离等于3.
同课章节目录
