初中数学北师大版八年级上册4.4一次函数的应用练习题(Word版 含解析)
文档属性
| 名称 | 初中数学北师大版八年级上册4.4一次函数的应用练习题(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 138.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-15 11:14:06 | ||
图片预览


文档简介
初中数学北师大版八年级上册第四章4一次函数的应用练习题
一、选择题
为了节约水资源,自来水公司按分段收费标准收费,如图所示反映的是每月收取水费元与用水量吨之间的函数关系.按照分段收费标准,小颖家三、四月份分别交水费29元和元,则四月份比三月份节约用水
A.
2吨
B.
吨
C.
3吨
D.
吨
有一个装有水的容器,如图所示,容器内的水面高度是10cm,现向容器内注水,并同时开始计时,在注水过程中,水面高度以每秒的速度匀速增加,则容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是
A.
正比例函数关系
B.
一次函数关系
C.
二次函数关系
D.
反比例函数关系
甲、乙两位同学住在同一小区,学校与小区相距2700米,一天甲从小区步行出发去学校,12分钟后乙也出发,乙先骑公交自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校.已知步行速度甲比乙每分钟快5米,图中的折线表示甲、乙两人之间的距离米与甲步行时间分钟的函数关系图象,则
A.
乙骑自行车的速度是180米分
B.
乙到还车点时,甲、乙两人相距850米
C.
自行车还车点距离学校300米
D.
乙到学校时,甲距离学校200米
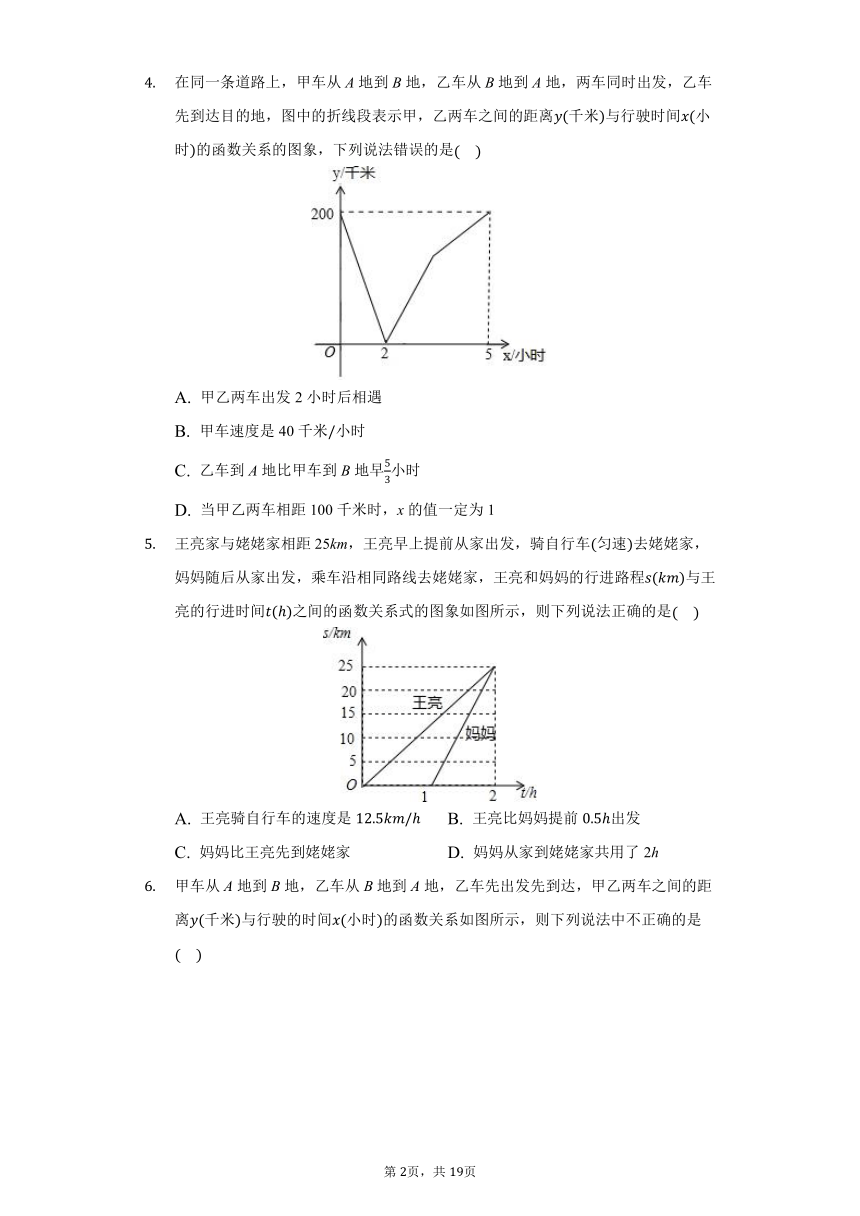
在同一条道路上,甲车从A地到B地,乙车从B地到A地,两车同时出发,乙车先到达目的地,图中的折线段表示甲,乙两车之间的距离千米与行驶时间小时的函数关系的图象,下列说法错误的是
A.
甲乙两车出发2小时后相遇
B.
甲车速度是40千米小时
C.
乙车到A地比甲车到B地早小时
D.
当甲乙两车相距100千米时,x的值一定为1
王亮家与姥姥家相距25km,王亮早上提前从家出发,骑自行车匀速去姥姥家,妈妈随后从家出发,乘车沿相同路线去姥姥家,王亮和妈妈的行进路程与王亮的行进时间之间的函数关系式的图象如图所示,则下列说法正确的是
A.
王亮骑自行车的速度是
B.
王亮比妈妈提前出发
C.
妈妈比王亮先到姥姥家
D.
妈妈从家到姥姥家共用了2h
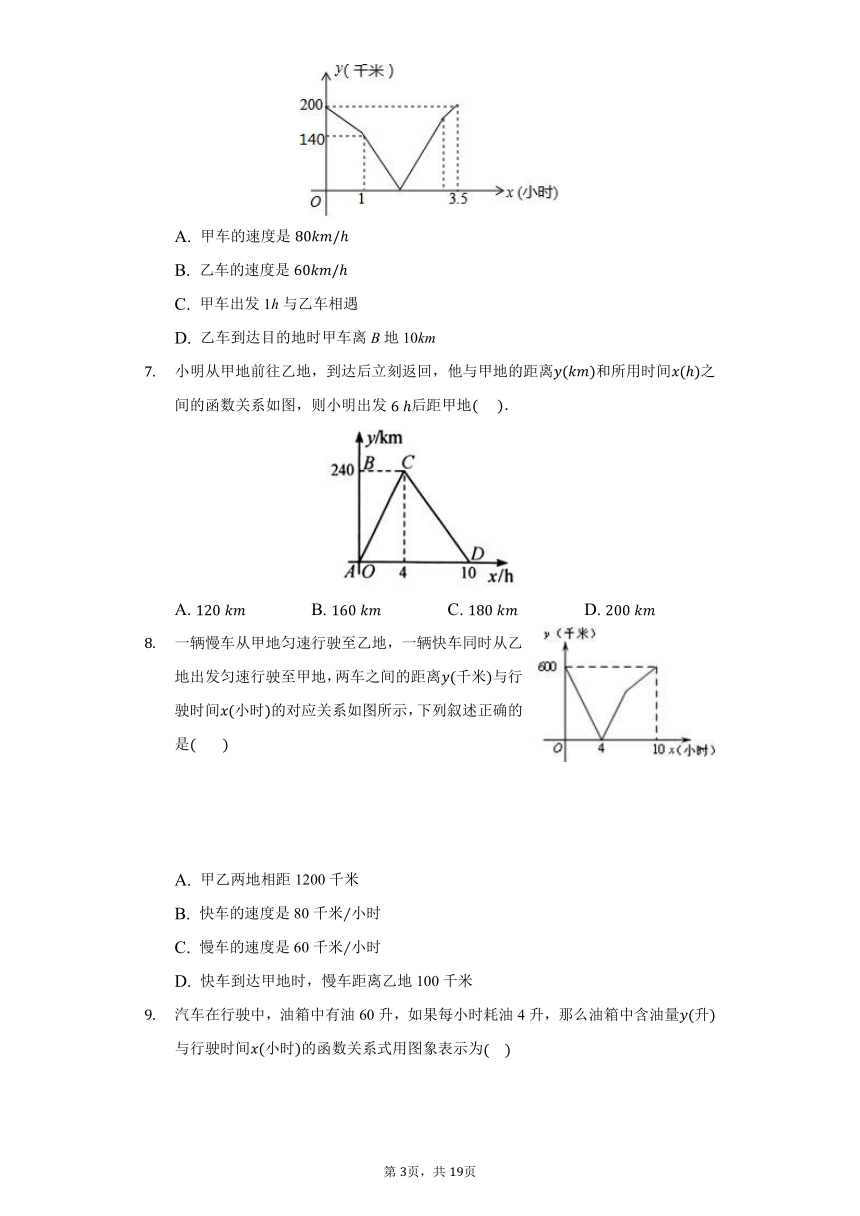
甲车从A地到B地,乙车从B地到A地,乙车先出发先到达,甲乙两车之间的距离千米与行驶的时间小时的函数关系如图所示,则下列说法中不正确的是
A.
甲车的速度是
B.
乙车的速度是
C.
甲车出发1h与乙车相遇
D.
乙车到达目的地时甲车离?B地10km
小明从甲地前往乙地,到达后立刻返回,他与甲地的距离和所用时间之间的函数关系如图,则小明出发后距甲地???
.
A.
B.
C.
D.
一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离千米与行驶时间小时的对应关系如图所示,下列叙述正确的是?
?
?
A.
甲乙两地相距1200千米
B.
快车的速度是80千米小时
C.
慢车的速度是60千米小时
D.
快车到达甲地时,慢车距离乙地100千米
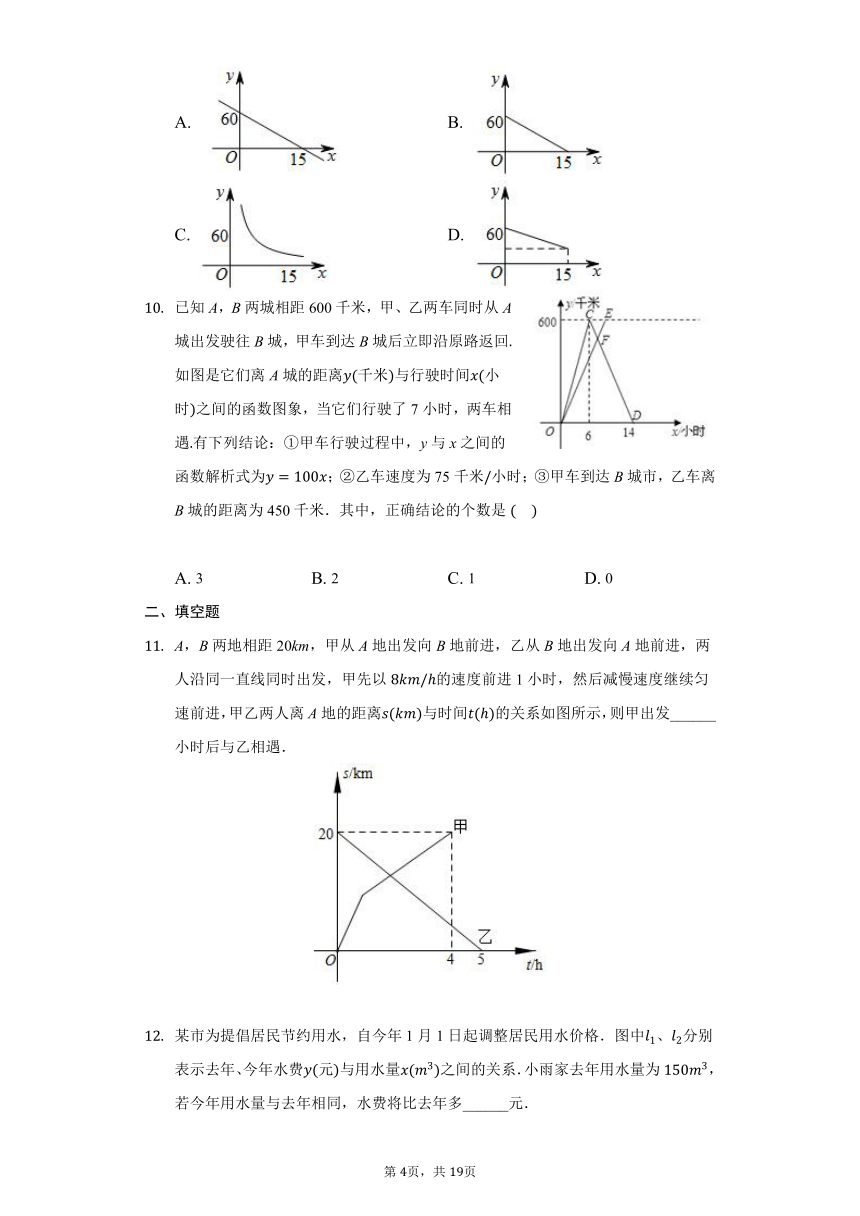
汽车在行驶中,油箱中有油60升,如果每小时耗油4升,那么油箱中含油量升与行驶时间小时的函数关系式用图象表示为
A.
B.
C.
D.
已知A,B两城相距600千米,甲、乙两车同时从A城出发驶往B城,甲车到达B城后立即沿原路返回如图是它们离A城的距离千米与行驶时间小时之间的函数图象,当它们行驶了7小时,两车相遇有下列结论:甲车行驶过程中,y与x之间的函数解析式为;乙车速度为75千米小时;甲车到达B城市,乙车离B城的距离为450千米.其中,正确结论的个数是?????
A.
3
B.
2
C.
1
D.
0
二、填空题
A,B两地相距20km,甲从A地出发向B地前进,乙从B地出发向A地前进,两人沿同一直线同时出发,甲先以的速度前进1小时,然后减慢速度继续匀速前进,甲乙两人离A地的距离与时间的关系如图所示,则甲出发______小时后与乙相遇.
某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中、分别表示去年、今年水费元与用水量之间的关系.小雨家去年用水量为,若今年用水量与去年相同,水费将比去年多______元.
十一黄金周,小明和小亮乘甲车从沙坪坝出发,以一定的速度匀速前往铁山坪体验“飞越丛林”出发15分钟后,小明发现忘带身份证和钱包,便下车换乘乙车匀速回家去取小明换车、取身份证和钱包的时间忽略不计,小亮仍乘甲车并以原速继续前行,小明回家取了身份证和钱包后,为节约时间,又立即乘乙车以原来速度的倍匀速按原路赶往铁山坪,由于国庆期间车流量较大,在小明乘乙车以加速后的速度匀速赶往铁山坪期间,甲车恰好因故在途中持续堵塞了5分钟,结果乙车先到达目的地.甲、乙两车之间的距离千米与乙车行驶时间小时之间的部分图象如图所示,则乙车出发______小时到达目的地.
甲乙两地相距880千米,一辆汽车平均以每小时110千米的速度从甲地开往乙地,t小时后汽年距离乙地s千米,写出s与t之间的关系式______,并写出t的取值范围______.
某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶,在行驶过程中,油箱的余油量升与行驶时间小时之间的关系如表:
小时
0
1
2
3
升
120
112
104
96
由表格中y与t的关系可知,当汽车行驶______小时,油箱的余油量为0.
三、解答题
某商场计划购进A,B两种新型节能台灯共200盏,这两种台灯的进价、售价如下表所示:
价格
类型
进价元盏
售价元盏
A型
30
45
B型
50
70
若商场预计进货款为7000元,则两种台灯各购进多少盏?
若商场规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时利润最大?此时利润为多少元.
如图,和分别是走私船和我公安快艇航行路程与时间的函数图象,请结合图象解决下列问题:
在刚出发时,我公安快艇距走私船多少海里?
计算走私船与公安艇的速度分别是多少?
求出,的解析式.
问6分钟时,走私船与我公安快艇相距多少海里?
星期五小颖放学步行从学校回家,当她走了一段路后,想起要去买彩笔做画报,于是原路返回到刚经过的文具用品店.买到彩笔后继续往家走如图是她离家的距离与所用时间的关系示意图,请根据图中提供的信息回答下列问题:
小颖家与学校的距离是______米;
表示的实际意义是______;
小颖本次从学校回家的整个过程中,走的路程是多少米?
买到彩笔后,小颖从文具用品店回到家步行的速度是多少米分?
某商场为了庆祝正式开业,推出了两种购物方案,方案一、非会员购物时,所有商品价格可获得九五折优惠;方案二、如果交纳300元会费成为该商场的会员,则所有商品的价格可获九折优惠.
以元表示商品价格,元表示支出金额,分别写出两种购物方案中y关于x的函数表达式;
若某人计划在该商场购买价格为5880元的电脑一台,请分析哪种方案更省钱.
答案和解析
1.【答案】C
【解析】解:当时,设,
将点代入可得:,
解得:,
即可得:,
当时,设y与x的函数关系式为:,
当时,,当时,,
将它们分别代入中得:,
解得:,
那么y与x的函数关系式为:,
综上可得:,
当时,知道,将代入得,
解得,
当时,知道,将代入得,
解得:,
即可得四月份比三月份节约用水:吨.
故选:C.
先设函数解析式,然后看图将对应值代入其中求出常数项,即可得到函数解析式,根据函数解析式求出四月份的水量,三月份水量可直接求,那么四月份比三月份节约用水多少可求出.
本题考查了识别函数图象的能力,是一道较为简单的题,观察图象提供的信息,再分析10吨水以内和超过10吨水价格的不同分别求出解析式.
2.【答案】B
【解析】解:设容器内的水面高度为h,注水时间为t,根据题意得:
,
容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是一次函数关系.
故选:B.
根据题意可得容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系式,进而判断出相应函数类型.
本题主要考查了一次函数的应用,观察图象提供的信息,再分析高度、时间和容积的关系即可找到解题关键.
3.【答案】C
【解析】解:甲步行的速度为:米分,
乙骑自行车的速度为:米分,
故选项A错误;
乙步行的速度为:米分,
乙全程:,解得,
所以乙骑自行车的路程为:米,
所以自行车还车点距离学校为:米,
故选项C正确;
乙到还车点时,乙的路程为3000米,甲步行的路程为:米,
此时两人相距:米,
故选项B错误;
乙到学校时,甲的路程为:米,
此时甲离学校:米.
故选项D错误.
故选:C.
根据甲12分钟步行了960米可得甲步行的速度,根据乙骑自行车8分钟行驶的路程比甲多960米即可得出乙骑自行车的速度;根据乙骑自行车的速度和乙步行的速度求出求出c的值,进而求出乙到还车点时,甲、乙两人的距离;同时可以求出自行车还车点到学校的距离;根据乙在甲出发31分后到达学校,即可求出乙到学校时,甲到学校的距离.
本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.
4.【答案】D
【解析】解:出发2h后,其距离为零,即两车相遇,故选项A说法正确;
甲的速度是,故选项B说法正确;
乙的速度为:,乙行驶的时间为,乙车到A地比甲车到B地早:,故选项C说法正确;
设出发x小时后,甲乙两车相距100千米,则或,解得或,故选项D说法错误.
故选:D.
根据相遇时距离为0,即甲乙两车出发2小时后相遇;根据图象分别分析甲、乙两车的速度,进而分析得出答案.
本题考查了一次函数的应用、行程问题的数量关系速度路程时间的运用,速度和的运用,解答时正确理解函数图象的数据的意义是关键.
5.【答案】A
【解析】解:由图象可知,
王亮骑自行车的速度是:,故选项A正确;
王亮比妈妈提前1h出发,故选项B错误;
妈妈和王亮同时到姥姥家,故选项C错误;
妈妈从家到姥姥家用了1h,故选项D错误;
故选:A.
根据函数图象,可以分别判断各选项是否正确,本题得以解决.
本题考查一次函数的应用,解题的关键是明确题意,利用数形结合的思想解答问题.
6.【答案】D
【解析】解:根据图象可知甲用了小时走了200千米,所以甲的速度为:,故选项A不合题意;
由图象横坐标可得,乙先出发的时间为1小时,两车相距,故乙车的速度是,故选项B不符合题意;
小时,即甲车出发1h与乙车相遇,故选项C不合题意;
,即乙车到达目的地时甲车离B地,故选项D符合题意.
故选:D.
根据已知图象分别分析甲、乙两车的速度,进而分析得出答案.
本题考查了利用函数的图象解决实际问题,解决本题的关键正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.
7.【答案】B
【解析】
【分析】
本题考查一次函数的应用,待定系数法求一次函数解析式当时,设y与之间的函数表达式为,把和分别代入得解析式,再计算当时的函数值即可.
【解答】
解:当时,设y与之间的函数表达式为,
把和分别代入
得
解得
即当时,y与之间的函数表达式为
.
当时,
,
即小明出发6h后距甲地160km.
故选B.
8.【答案】C
【解析】
【分析】
本题此题主要考查了一次函数的应用有关知识.
A、由图象容易得出答案;
B、设快车速度为x千米小时,由图象得出方程,解方程即可;
C、由题意得出慢车速度千米小时;
D、求出快车到达甲地所用时间,进一步求得慢车行驶的路程,用600减去该路程即可得出答案.
【解答】
解:A、由图象得:甲乙两地相距600千米,故选项错误;
B、由题意得:慢车总用时10小时,
慢车速度为千米小时;
设快车速度为x千米小时,
由图象得:,解得:,
快车速度为90千米小时,故选项错误;
慢车速度为60千米小时;
C、慢车速度为60千米小时,故选项正确;
D、小时,千米,
千米,
故快车到达甲地时,慢车距离乙地200千米,故选项错误.
故选C.
9.【答案】B
【解析】
【分析】
本题考查的知识点是一次函数的应用,一次函数的图象,根据剩余油量原有油量消耗的油量得到x,y的函数关系式,再根据一次函数的图象解答.
【解答】
解:根据题意,,
当时,,
当时,,
解得,
所以,x的取值范围为,
函数图象与x轴的交点为,与y轴的交点为,
故选B.
10.【答案】C
【解析】
【分析】
本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,行程问题的相遇问题,读懂题目信息,理解两车的行动过程是解题的关键.
根据函数图形,分,两段利用待定系数法求一次函数解析式解答,判断出错误;设乙车的速度为a千米小时,利用相遇问题列出方程求解即可判断出正确,再求出乙车行驶的路程,然后求出距离B城的距离判断出错误.
【解答】
解:时,,
时,设y与x的函数解析式为,
则,
解得,
所以,,
所以,甲车行驶过程中,,故错误;
设乙车的速度为a千米小时,
由题意得,,
解得,
乙车的速度为75千米小时,故正确;
乙车离B城的距离千米,故错误,
综上所述,正确结论是共1个.
故选:C.
11.【答案】2
【解析】解:甲减速后的速度为:,
一道速度为:,
设甲出发x小时后与乙相遇,根据题意得
,
解得.
即甲出发2小时后与乙相遇.
故答案为:2.
根据题意结合图象分别求出甲减速后的速度已经乙的速度,再列方程解答即可.
本题考查了一次函数的应用,解题的关键是读懂图象信息,灵活应用速度、路程、时间之间的关系解决问题.
12.【答案】210
【解析】解:设当时,对应的函数解析式为,
,得,
即当时,对应的函数解析式为,
当时,,
由图象可知,去年的水价是元,故小雨家去年用水量为,需要缴费:元,
元,
即小雨家去年用水量为,若今年用水量与去年相同,水费将比去年多210元,
故答案为:210.
根据函数图象中的数据可以求得时,对应的函数解析式,从而可以求得时对应的函数值,由的的图象可以求得时对应的函数值,从而可以计算出题目中所求问题的答案,本题得以解决.
本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.
13.【答案】
【解析】解:设甲车的速度为a千米小时,乙车回家时的速度是b千米小时,
,
,
设,,
由图象得乙车行驶小时两边相距千米,
,
,
,,
设t小时两车相距3千米,
,
,
故答案为:.
设两家出发时,速度是a千米小时,小明返回家时速度是b千米小时,根据甲车15分走的路程等于返回时小时走的路程,由此可得a与b的关系,表示,,根据两车相距列方程可得m的值,从而得a和b的值,最后根据两车相距3千米列方程可解答.
本题考查一次函数的应用,一元一次方程的应用等知识,解题的关键是读懂图象信息,属于中考常考题型.
14.【答案】?
【解析】解:由题意可得:,t的取值范围是:.
故答案为:;.
直接利用总路程行驶的距离距离乙地的距离进而得出答案.
此题主要考查了一次函数的应用,正确表示出行驶的路程是解题关键.
15.【答案】15
【解析】解:由表格可知,每行驶1小时,耗油8升,
时,,
油箱中有油120升,
小时,
当行驶15小时时,油箱的余油量为0,
故答案为15.
由表格可知油箱中有油120升,每行驶1小时,耗油8升,则可求解.
本题考查函数的表示方法;掌握用表格法表示函数,能够通过表格获取信息解题是关键.
16.【答案】解:设商场应购进A型台灯x盏,则B型台灯为盏,
根据题意得,,
解得,
所以,,
答:应购进A型台灯150盏,B型台灯50盏;
设商场销售完这批台灯可获利y元,
则,
,
,
即,
型台灯的进货数量不超过A型台灯数量的3倍,
,
,
,y随x的增大而减小,
时,y取得最大值,为元
答:商场购进A型台灯50盏,B型台灯150盏,销售完这批台灯时获利最多,此时利润为3750元.
【解析】设商场应购进A型台灯x盏,表示出B型台灯为盏,然后根据进货款型台灯的进货款型台灯的进货款列出方程求解即可;
设商场销售完这批台灯可获利y元,根据获利等于两种台灯的获利总和列式整理,再求出x的取值范围,然后根据一次函数的增减性求出获利的最大值.
本题考查了一次函数的应用,主要利用了一次函数的增减性,题中理清题目数量关系并列式求出x的取值范围是解题的关键.
17.【答案】解:当时,,,
,
在刚出发时,我公安快艇距走私船5海里.
海里分钟,
海里分钟.
走私船的速度是1海里分钟,公安艇的速度为海里分钟.
设图象的解析式为,
将,代入,得:
,解得:,
图象的解析式为;
设图象的解析式为,
将代入,得:
,解得:,
图象的解析式为.
当时,,,
海里,
分钟时,走私船与我公安快艇相距2海里.
【解析】由当时,,,二者做差后即可得出结论;
利用速度路程时间,可分别求出走私船与公安艇的速度;
观察函数图象,找出点的坐标,利用待定系数法即可求出,的解析式;
利用一次函数图象上点的坐标特征,求出时,,的值,做差后即可得出结论.
本题考查了待定系数法求一次函数解析式、函数图象以及一次函数图象上点的坐标特征,解题的关键是:观察函数图象,找出当时y的值;利用速度路程时间求出两船的速度;根据点的坐标,利用待定系数法求出一次函数解析式;利用一次函数图象上点的坐标特征求出当时,的值.
18.【答案】2600?
小颖在文具用品店买彩笔所花时间
【解析】解:小颖家与学校的距离是2600米;
故答案为:2600;
表示的实际意义是小颖在文具用品店买彩笔所花时间;
故答案为:小颖在文具用品店买彩笔所花时间;
米,
答:小颖本次从学校回家的整个过程中,走的路程是3400米;
米分,
买到彩笔后,小颖从文具用品店回到家步行的速度是90米分.
根据函数图象,小颖家与学校的距离是2600米;
表示的实际意义是小颖在文具用品店买彩笔所花时间;
小颖本次从学校回家的整个过程中,走的路程是;
根据速度路程时间,即可解答.
本题主要考查了函数图象的读图能力,要理解横纵坐标表示的含义以及小颖的运动过程是解题的关键.
19.【答案】解:按方案一购买,需付款元;?????
按方案二购买,需付款元;
当时,
方案一:,
方案二:,
所以选择方案一更省钱.
【解析】根据题意分别得出两种优惠方案的关系式即可;
将已知数据代入中代数式求出即可.
此题考查一次函数的应用,解决问题的关键是读懂题意,正确列出函数解析式是解题的关键.
第2页,共2页
第1页,共1页
一、选择题
为了节约水资源,自来水公司按分段收费标准收费,如图所示反映的是每月收取水费元与用水量吨之间的函数关系.按照分段收费标准,小颖家三、四月份分别交水费29元和元,则四月份比三月份节约用水
A.
2吨
B.
吨
C.
3吨
D.
吨
有一个装有水的容器,如图所示,容器内的水面高度是10cm,现向容器内注水,并同时开始计时,在注水过程中,水面高度以每秒的速度匀速增加,则容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是
A.
正比例函数关系
B.
一次函数关系
C.
二次函数关系
D.
反比例函数关系
甲、乙两位同学住在同一小区,学校与小区相距2700米,一天甲从小区步行出发去学校,12分钟后乙也出发,乙先骑公交自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校.已知步行速度甲比乙每分钟快5米,图中的折线表示甲、乙两人之间的距离米与甲步行时间分钟的函数关系图象,则
A.
乙骑自行车的速度是180米分
B.
乙到还车点时,甲、乙两人相距850米
C.
自行车还车点距离学校300米
D.
乙到学校时,甲距离学校200米
在同一条道路上,甲车从A地到B地,乙车从B地到A地,两车同时出发,乙车先到达目的地,图中的折线段表示甲,乙两车之间的距离千米与行驶时间小时的函数关系的图象,下列说法错误的是
A.
甲乙两车出发2小时后相遇
B.
甲车速度是40千米小时
C.
乙车到A地比甲车到B地早小时
D.
当甲乙两车相距100千米时,x的值一定为1
王亮家与姥姥家相距25km,王亮早上提前从家出发,骑自行车匀速去姥姥家,妈妈随后从家出发,乘车沿相同路线去姥姥家,王亮和妈妈的行进路程与王亮的行进时间之间的函数关系式的图象如图所示,则下列说法正确的是
A.
王亮骑自行车的速度是
B.
王亮比妈妈提前出发
C.
妈妈比王亮先到姥姥家
D.
妈妈从家到姥姥家共用了2h
甲车从A地到B地,乙车从B地到A地,乙车先出发先到达,甲乙两车之间的距离千米与行驶的时间小时的函数关系如图所示,则下列说法中不正确的是
A.
甲车的速度是
B.
乙车的速度是
C.
甲车出发1h与乙车相遇
D.
乙车到达目的地时甲车离?B地10km
小明从甲地前往乙地,到达后立刻返回,他与甲地的距离和所用时间之间的函数关系如图,则小明出发后距甲地???
.
A.
B.
C.
D.
一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离千米与行驶时间小时的对应关系如图所示,下列叙述正确的是?
?
?
A.
甲乙两地相距1200千米
B.
快车的速度是80千米小时
C.
慢车的速度是60千米小时
D.
快车到达甲地时,慢车距离乙地100千米
汽车在行驶中,油箱中有油60升,如果每小时耗油4升,那么油箱中含油量升与行驶时间小时的函数关系式用图象表示为
A.
B.
C.
D.
已知A,B两城相距600千米,甲、乙两车同时从A城出发驶往B城,甲车到达B城后立即沿原路返回如图是它们离A城的距离千米与行驶时间小时之间的函数图象,当它们行驶了7小时,两车相遇有下列结论:甲车行驶过程中,y与x之间的函数解析式为;乙车速度为75千米小时;甲车到达B城市,乙车离B城的距离为450千米.其中,正确结论的个数是?????
A.
3
B.
2
C.
1
D.
0
二、填空题
A,B两地相距20km,甲从A地出发向B地前进,乙从B地出发向A地前进,两人沿同一直线同时出发,甲先以的速度前进1小时,然后减慢速度继续匀速前进,甲乙两人离A地的距离与时间的关系如图所示,则甲出发______小时后与乙相遇.
某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中、分别表示去年、今年水费元与用水量之间的关系.小雨家去年用水量为,若今年用水量与去年相同,水费将比去年多______元.
十一黄金周,小明和小亮乘甲车从沙坪坝出发,以一定的速度匀速前往铁山坪体验“飞越丛林”出发15分钟后,小明发现忘带身份证和钱包,便下车换乘乙车匀速回家去取小明换车、取身份证和钱包的时间忽略不计,小亮仍乘甲车并以原速继续前行,小明回家取了身份证和钱包后,为节约时间,又立即乘乙车以原来速度的倍匀速按原路赶往铁山坪,由于国庆期间车流量较大,在小明乘乙车以加速后的速度匀速赶往铁山坪期间,甲车恰好因故在途中持续堵塞了5分钟,结果乙车先到达目的地.甲、乙两车之间的距离千米与乙车行驶时间小时之间的部分图象如图所示,则乙车出发______小时到达目的地.
甲乙两地相距880千米,一辆汽车平均以每小时110千米的速度从甲地开往乙地,t小时后汽年距离乙地s千米,写出s与t之间的关系式______,并写出t的取值范围______.
某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶,在行驶过程中,油箱的余油量升与行驶时间小时之间的关系如表:
小时
0
1
2
3
升
120
112
104
96
由表格中y与t的关系可知,当汽车行驶______小时,油箱的余油量为0.
三、解答题
某商场计划购进A,B两种新型节能台灯共200盏,这两种台灯的进价、售价如下表所示:
价格
类型
进价元盏
售价元盏
A型
30
45
B型
50
70
若商场预计进货款为7000元,则两种台灯各购进多少盏?
若商场规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时利润最大?此时利润为多少元.
如图,和分别是走私船和我公安快艇航行路程与时间的函数图象,请结合图象解决下列问题:
在刚出发时,我公安快艇距走私船多少海里?
计算走私船与公安艇的速度分别是多少?
求出,的解析式.
问6分钟时,走私船与我公安快艇相距多少海里?
星期五小颖放学步行从学校回家,当她走了一段路后,想起要去买彩笔做画报,于是原路返回到刚经过的文具用品店.买到彩笔后继续往家走如图是她离家的距离与所用时间的关系示意图,请根据图中提供的信息回答下列问题:
小颖家与学校的距离是______米;
表示的实际意义是______;
小颖本次从学校回家的整个过程中,走的路程是多少米?
买到彩笔后,小颖从文具用品店回到家步行的速度是多少米分?
某商场为了庆祝正式开业,推出了两种购物方案,方案一、非会员购物时,所有商品价格可获得九五折优惠;方案二、如果交纳300元会费成为该商场的会员,则所有商品的价格可获九折优惠.
以元表示商品价格,元表示支出金额,分别写出两种购物方案中y关于x的函数表达式;
若某人计划在该商场购买价格为5880元的电脑一台,请分析哪种方案更省钱.
答案和解析
1.【答案】C
【解析】解:当时,设,
将点代入可得:,
解得:,
即可得:,
当时,设y与x的函数关系式为:,
当时,,当时,,
将它们分别代入中得:,
解得:,
那么y与x的函数关系式为:,
综上可得:,
当时,知道,将代入得,
解得,
当时,知道,将代入得,
解得:,
即可得四月份比三月份节约用水:吨.
故选:C.
先设函数解析式,然后看图将对应值代入其中求出常数项,即可得到函数解析式,根据函数解析式求出四月份的水量,三月份水量可直接求,那么四月份比三月份节约用水多少可求出.
本题考查了识别函数图象的能力,是一道较为简单的题,观察图象提供的信息,再分析10吨水以内和超过10吨水价格的不同分别求出解析式.
2.【答案】B
【解析】解:设容器内的水面高度为h,注水时间为t,根据题意得:
,
容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是一次函数关系.
故选:B.
根据题意可得容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系式,进而判断出相应函数类型.
本题主要考查了一次函数的应用,观察图象提供的信息,再分析高度、时间和容积的关系即可找到解题关键.
3.【答案】C
【解析】解:甲步行的速度为:米分,
乙骑自行车的速度为:米分,
故选项A错误;
乙步行的速度为:米分,
乙全程:,解得,
所以乙骑自行车的路程为:米,
所以自行车还车点距离学校为:米,
故选项C正确;
乙到还车点时,乙的路程为3000米,甲步行的路程为:米,
此时两人相距:米,
故选项B错误;
乙到学校时,甲的路程为:米,
此时甲离学校:米.
故选项D错误.
故选:C.
根据甲12分钟步行了960米可得甲步行的速度,根据乙骑自行车8分钟行驶的路程比甲多960米即可得出乙骑自行车的速度;根据乙骑自行车的速度和乙步行的速度求出求出c的值,进而求出乙到还车点时,甲、乙两人的距离;同时可以求出自行车还车点到学校的距离;根据乙在甲出发31分后到达学校,即可求出乙到学校时,甲到学校的距离.
本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.
4.【答案】D
【解析】解:出发2h后,其距离为零,即两车相遇,故选项A说法正确;
甲的速度是,故选项B说法正确;
乙的速度为:,乙行驶的时间为,乙车到A地比甲车到B地早:,故选项C说法正确;
设出发x小时后,甲乙两车相距100千米,则或,解得或,故选项D说法错误.
故选:D.
根据相遇时距离为0,即甲乙两车出发2小时后相遇;根据图象分别分析甲、乙两车的速度,进而分析得出答案.
本题考查了一次函数的应用、行程问题的数量关系速度路程时间的运用,速度和的运用,解答时正确理解函数图象的数据的意义是关键.
5.【答案】A
【解析】解:由图象可知,
王亮骑自行车的速度是:,故选项A正确;
王亮比妈妈提前1h出发,故选项B错误;
妈妈和王亮同时到姥姥家,故选项C错误;
妈妈从家到姥姥家用了1h,故选项D错误;
故选:A.
根据函数图象,可以分别判断各选项是否正确,本题得以解决.
本题考查一次函数的应用,解题的关键是明确题意,利用数形结合的思想解答问题.
6.【答案】D
【解析】解:根据图象可知甲用了小时走了200千米,所以甲的速度为:,故选项A不合题意;
由图象横坐标可得,乙先出发的时间为1小时,两车相距,故乙车的速度是,故选项B不符合题意;
小时,即甲车出发1h与乙车相遇,故选项C不合题意;
,即乙车到达目的地时甲车离B地,故选项D符合题意.
故选:D.
根据已知图象分别分析甲、乙两车的速度,进而分析得出答案.
本题考查了利用函数的图象解决实际问题,解决本题的关键正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.
7.【答案】B
【解析】
【分析】
本题考查一次函数的应用,待定系数法求一次函数解析式当时,设y与之间的函数表达式为,把和分别代入得解析式,再计算当时的函数值即可.
【解答】
解:当时,设y与之间的函数表达式为,
把和分别代入
得
解得
即当时,y与之间的函数表达式为
.
当时,
,
即小明出发6h后距甲地160km.
故选B.
8.【答案】C
【解析】
【分析】
本题此题主要考查了一次函数的应用有关知识.
A、由图象容易得出答案;
B、设快车速度为x千米小时,由图象得出方程,解方程即可;
C、由题意得出慢车速度千米小时;
D、求出快车到达甲地所用时间,进一步求得慢车行驶的路程,用600减去该路程即可得出答案.
【解答】
解:A、由图象得:甲乙两地相距600千米,故选项错误;
B、由题意得:慢车总用时10小时,
慢车速度为千米小时;
设快车速度为x千米小时,
由图象得:,解得:,
快车速度为90千米小时,故选项错误;
慢车速度为60千米小时;
C、慢车速度为60千米小时,故选项正确;
D、小时,千米,
千米,
故快车到达甲地时,慢车距离乙地200千米,故选项错误.
故选C.
9.【答案】B
【解析】
【分析】
本题考查的知识点是一次函数的应用,一次函数的图象,根据剩余油量原有油量消耗的油量得到x,y的函数关系式,再根据一次函数的图象解答.
【解答】
解:根据题意,,
当时,,
当时,,
解得,
所以,x的取值范围为,
函数图象与x轴的交点为,与y轴的交点为,
故选B.
10.【答案】C
【解析】
【分析】
本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,行程问题的相遇问题,读懂题目信息,理解两车的行动过程是解题的关键.
根据函数图形,分,两段利用待定系数法求一次函数解析式解答,判断出错误;设乙车的速度为a千米小时,利用相遇问题列出方程求解即可判断出正确,再求出乙车行驶的路程,然后求出距离B城的距离判断出错误.
【解答】
解:时,,
时,设y与x的函数解析式为,
则,
解得,
所以,,
所以,甲车行驶过程中,,故错误;
设乙车的速度为a千米小时,
由题意得,,
解得,
乙车的速度为75千米小时,故正确;
乙车离B城的距离千米,故错误,
综上所述,正确结论是共1个.
故选:C.
11.【答案】2
【解析】解:甲减速后的速度为:,
一道速度为:,
设甲出发x小时后与乙相遇,根据题意得
,
解得.
即甲出发2小时后与乙相遇.
故答案为:2.
根据题意结合图象分别求出甲减速后的速度已经乙的速度,再列方程解答即可.
本题考查了一次函数的应用,解题的关键是读懂图象信息,灵活应用速度、路程、时间之间的关系解决问题.
12.【答案】210
【解析】解:设当时,对应的函数解析式为,
,得,
即当时,对应的函数解析式为,
当时,,
由图象可知,去年的水价是元,故小雨家去年用水量为,需要缴费:元,
元,
即小雨家去年用水量为,若今年用水量与去年相同,水费将比去年多210元,
故答案为:210.
根据函数图象中的数据可以求得时,对应的函数解析式,从而可以求得时对应的函数值,由的的图象可以求得时对应的函数值,从而可以计算出题目中所求问题的答案,本题得以解决.
本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.
13.【答案】
【解析】解:设甲车的速度为a千米小时,乙车回家时的速度是b千米小时,
,
,
设,,
由图象得乙车行驶小时两边相距千米,
,
,
,,
设t小时两车相距3千米,
,
,
故答案为:.
设两家出发时,速度是a千米小时,小明返回家时速度是b千米小时,根据甲车15分走的路程等于返回时小时走的路程,由此可得a与b的关系,表示,,根据两车相距列方程可得m的值,从而得a和b的值,最后根据两车相距3千米列方程可解答.
本题考查一次函数的应用,一元一次方程的应用等知识,解题的关键是读懂图象信息,属于中考常考题型.
14.【答案】?
【解析】解:由题意可得:,t的取值范围是:.
故答案为:;.
直接利用总路程行驶的距离距离乙地的距离进而得出答案.
此题主要考查了一次函数的应用,正确表示出行驶的路程是解题关键.
15.【答案】15
【解析】解:由表格可知,每行驶1小时,耗油8升,
时,,
油箱中有油120升,
小时,
当行驶15小时时,油箱的余油量为0,
故答案为15.
由表格可知油箱中有油120升,每行驶1小时,耗油8升,则可求解.
本题考查函数的表示方法;掌握用表格法表示函数,能够通过表格获取信息解题是关键.
16.【答案】解:设商场应购进A型台灯x盏,则B型台灯为盏,
根据题意得,,
解得,
所以,,
答:应购进A型台灯150盏,B型台灯50盏;
设商场销售完这批台灯可获利y元,
则,
,
,
即,
型台灯的进货数量不超过A型台灯数量的3倍,
,
,
,y随x的增大而减小,
时,y取得最大值,为元
答:商场购进A型台灯50盏,B型台灯150盏,销售完这批台灯时获利最多,此时利润为3750元.
【解析】设商场应购进A型台灯x盏,表示出B型台灯为盏,然后根据进货款型台灯的进货款型台灯的进货款列出方程求解即可;
设商场销售完这批台灯可获利y元,根据获利等于两种台灯的获利总和列式整理,再求出x的取值范围,然后根据一次函数的增减性求出获利的最大值.
本题考查了一次函数的应用,主要利用了一次函数的增减性,题中理清题目数量关系并列式求出x的取值范围是解题的关键.
17.【答案】解:当时,,,
,
在刚出发时,我公安快艇距走私船5海里.
海里分钟,
海里分钟.
走私船的速度是1海里分钟,公安艇的速度为海里分钟.
设图象的解析式为,
将,代入,得:
,解得:,
图象的解析式为;
设图象的解析式为,
将代入,得:
,解得:,
图象的解析式为.
当时,,,
海里,
分钟时,走私船与我公安快艇相距2海里.
【解析】由当时,,,二者做差后即可得出结论;
利用速度路程时间,可分别求出走私船与公安艇的速度;
观察函数图象,找出点的坐标,利用待定系数法即可求出,的解析式;
利用一次函数图象上点的坐标特征,求出时,,的值,做差后即可得出结论.
本题考查了待定系数法求一次函数解析式、函数图象以及一次函数图象上点的坐标特征,解题的关键是:观察函数图象,找出当时y的值;利用速度路程时间求出两船的速度;根据点的坐标,利用待定系数法求出一次函数解析式;利用一次函数图象上点的坐标特征求出当时,的值.
18.【答案】2600?
小颖在文具用品店买彩笔所花时间
【解析】解:小颖家与学校的距离是2600米;
故答案为:2600;
表示的实际意义是小颖在文具用品店买彩笔所花时间;
故答案为:小颖在文具用品店买彩笔所花时间;
米,
答:小颖本次从学校回家的整个过程中,走的路程是3400米;
米分,
买到彩笔后,小颖从文具用品店回到家步行的速度是90米分.
根据函数图象,小颖家与学校的距离是2600米;
表示的实际意义是小颖在文具用品店买彩笔所花时间;
小颖本次从学校回家的整个过程中,走的路程是;
根据速度路程时间,即可解答.
本题主要考查了函数图象的读图能力,要理解横纵坐标表示的含义以及小颖的运动过程是解题的关键.
19.【答案】解:按方案一购买,需付款元;?????
按方案二购买,需付款元;
当时,
方案一:,
方案二:,
所以选择方案一更省钱.
【解析】根据题意分别得出两种优惠方案的关系式即可;
将已知数据代入中代数式求出即可.
此题考查一次函数的应用,解决问题的关键是读懂题意,正确列出函数解析式是解题的关键.
第2页,共2页
第1页,共1页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
