人教版数学九年级上 24.2.2 直线和圆的位置关系测试题(Word版 含答案)
文档属性
| 名称 | 人教版数学九年级上 24.2.2 直线和圆的位置关系测试题(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 355.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-15 00:00:00 | ||
图片预览



文档简介
人教版数学九年级上《圆》的直线与圆的位置关系测试题
时间:100分钟
满分:120分
姓名:
一、选择题(每小题3分,共30分)
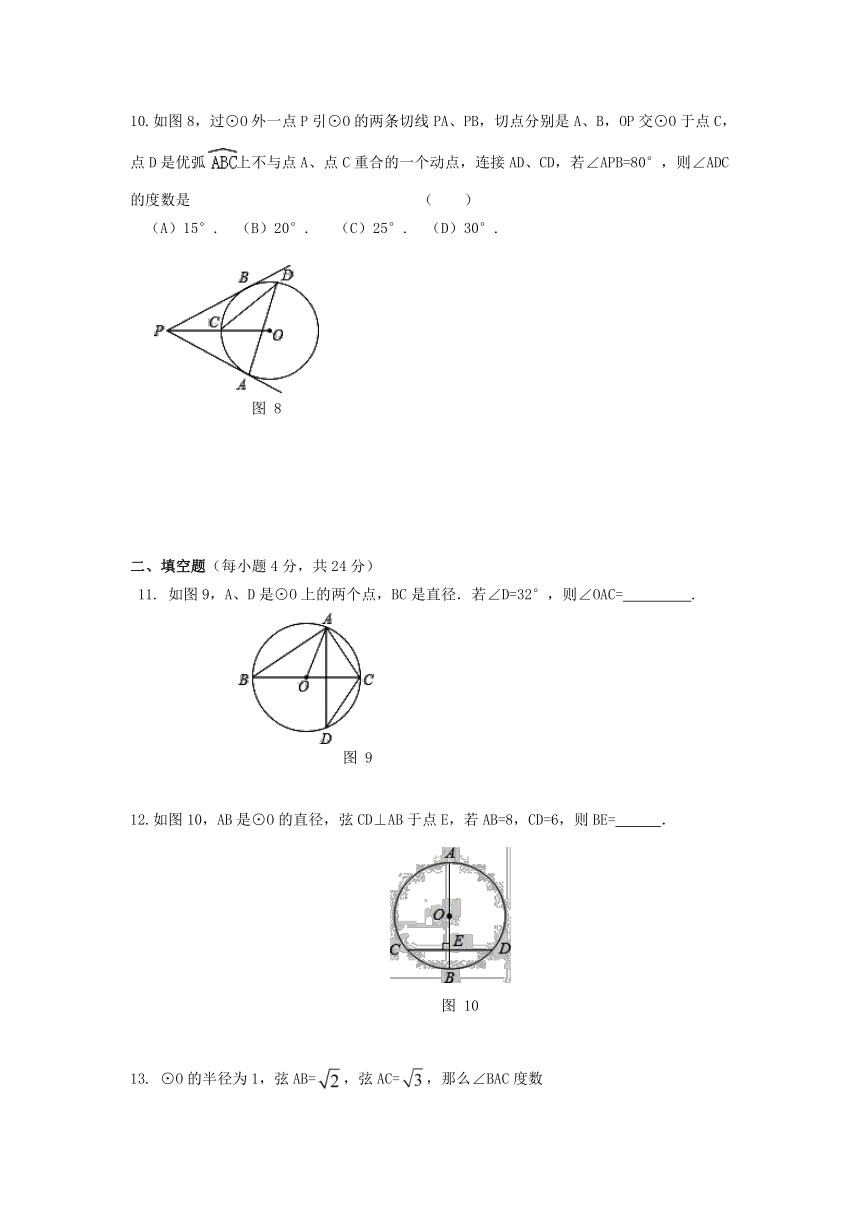
1.在公园的O处附近有E、F、G、H四棵树,位置如图1所示(图中小正方形的边长均相等),现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E、F、G、H四棵树中需要被移除的为
( )
(A)E、F、G.
(B)F、G、H.
(C)G、H、E.
(D)H、E、F.
图
1
2.下列图形中,不是中心对称图形的是
( )
3.如图2,CD是⊙O的直径,弦AB⊥CD于E,连接BC、BD,下列结论中不一定正确的是
( )
(A)AE=BE.
(B)=.
(C)OE=DE.
(D)∠DBC=90°.
图
2
4.如图3,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于
(
)
(A)12.5°.
(B)15°.
(C)20°.
(D)22.5°
图
3
5.下列条件,四边形ABCD一定有外接圆的是
( )
(A)∠A:∠B:∠C:∠D=1:3:3:4.
(B)∠A:∠B:∠C:∠D=2:3:3:5.
(C)∠A:∠B:∠C:∠D=2:3:3:5.
(D)∠A:∠B:∠C:∠D=2:3:3:2.
6.如图4,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则的长为
( )
(A)π.
(B)6π.
(C)3π.
(D)1.5π.
图
4
7.如图5,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是
( )
(A)25°.
(B)40°.
(C)50°.
(D)65°.
图
5
8.如图6示为4×4的网格图,A,B,C,D,O均在格点上,点O是
(
)
(A)△ACD的外心.
(B)△ABC的外心.
(C)△ACD的内心.
(D)△ABC的内心.
图
6
9.如图7,已知同心圆O,点P是大圆上一个定点,点A是小圆上的一个动点,连接PA,设PA的最大值为a,最小值为b,若大圆的半径为6,小圆的半径的2,则a+b的值为
( )
(A)9.
(B)10.
(C)12.
(D)14.
图
7
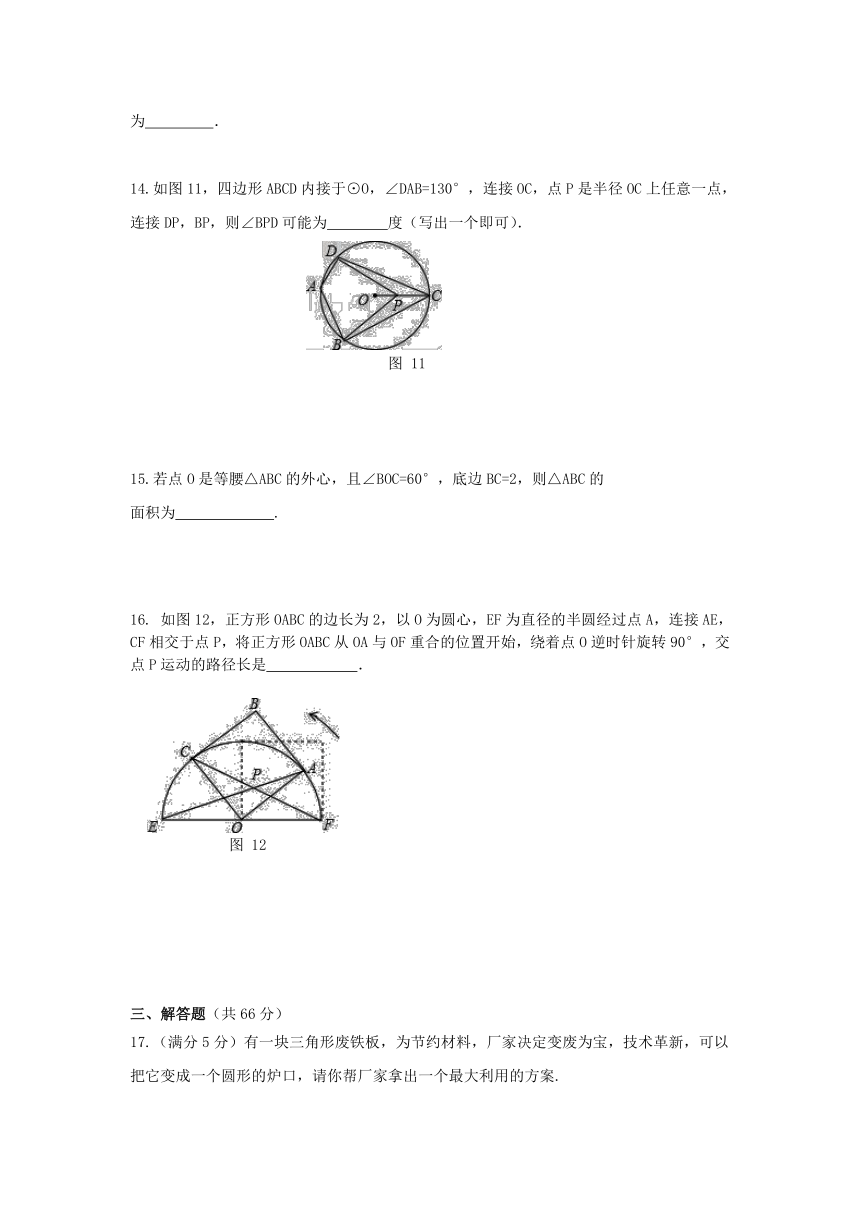
10.如图8,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是优弧上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=80°,则∠ADC的度数是
( )
(A)15°.
(B)20°.
(C)25°.
(D)30°.
图
8
二、填空题(每小题4分,共24分)
11.
如图9,A、D是⊙O上的两个点,BC是直径.若∠D=32°,则∠OAC=
.
图
9
12.如图10,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE=
.
图
10
13.
⊙O的半径为1,弦AB=,弦AC=,那么∠BAC度数
为
.
14.如图11,四边形ABCD内接于⊙O,∠DAB=130°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为
度(写出一个即可).
图
11
15.若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=2,则△ABC的
面积为
.
16.
如图12,正方形OABC的边长为2,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是 .
图
12
三、解答题(共66分)
17.(满分5分)有一块三角形废铁板,为节约材料,厂家决定变废为宝,技术革新,可以把它变成一个圆形的炉口,请你帮厂家拿出一个最大利用的方案.
18.
(满分8分)如图13,CD是Rt△ABC斜边AB上高,⊙是三角形ACD的内切圆,半径为,⊙是三角形BCD的内切圆,半径为,设三角形ABC的三边长分别为a,b,c.
(1)用a,b,c分别表示,;
(2)计算的值.
图
13
19.
(满分8分)如图14,AB为⊙O的直径,AB=6,AB⊥弦CD,垂足为G,EF切⊙O于点B,∠A=30°,
连接AD、OC、BC,求证:(1)∠EBC=30°;(2)求弧BC的长度.
图
14
20.
(满分8分)已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=,其中a,b,c是三角形的三边长,p=,S是三角形的面积,并给出了证明.
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
因为a=3,b=4,c=5
所以p==6
所以S===6
事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
如图15,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
图
15
21.
(满分8分)如图16,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根号和π)
图
16
22.
(满分8分)如图17所示,点E是直角三角形ABC斜边AB的中点,点D是三角形ABC的内心,且∠A=30°.
(1)求证:DE=DC;
(2)求∠DEC的度数.
图
17
23.
(满分9分)如图18,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,过点D作DE∥AB交圆O于点E
(1)证明点C在圆O上;(2)求tan∠CDE的值;
(3)求圆心O到弦ED的距离.
图
18
24.
(满分12分)如图19,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M,其中P点在AQ(弧)上且不与A点重合,但Q点可与B点重合.
发现
AP(弧)的长与QB(弧)的长之和为定值m,求m;
思考
点M与AB的最大距离为_______,此时点P,A间的距离为_______;
点M与AB的最小距离为________,此时半圆M的弧与AB所围成的封闭图形面积
为________.
探究
当半圆M与AB相切时,求AP(弧)的长.
(注:结果保留π,cos
35°=,cos
55°=)
图
19
参考答案:
直线与圆的位置关系测试题
一、选择题
1.(A)
提示:OA=,则OE=2<OA,点E在⊙O内,OF=2<OA,点F在⊙O内,OG=1<OA,点G在⊙O内,OH=>OA,点H在⊙O外.
2.(B)
提示:旋转180度后仍能与原来图形重合的图形是中心对称图形.
3.(C)
提示:根据垂径定理去一一判定,只有C是没有条件支撑.
4.
(B)
提示:
连接OB,因为四边形ABCO是平行四边形,OA=OC,所以四边形ABCO是菱形.
所以△AOB为等边三角形,因为OF⊥OC,OC∥AB,所以OF⊥AB,
所以∠BOF=∠AOF=30°,由圆周角定理得∠BAF=∠BOF=15°.
5.(D)
提示:
圆的内接四边形对角互补,所以对角和所占比数和相等.
6.
(D)
提示:所在扇形是扇形AOB,其半径是OA,其圆心角是∠AOB,半径OA=3,旋转角度为90°,所以∠AOB=90°,所以的长为:=1.5π.
7.
(B)
提示:
连接OC,由∠A=25°,可求得∠BOC的度数,由CD是圆O的切线,可得OC⊥CD,继而求得答案.
8.(B)
提示:计算O到A,B,C,D的距离,OA=OB=OC,根据定义知点O是三角形ABC的外心.
9.
(C)
提示:当P,O,A共线时,PA与小圆的有两个交点,远离P的那个交点,PA最大,此时a=6+2=8;
靠近P的交点,PA值最小,此时b=6-2=4,所以a+b=12.
10.
(C)
提示:由切线性质,得
∠BOA=360°﹣90°﹣90°﹣80°=100°,
由=,得∠AOC=∠BOC=50°.由圆周角定理,得∠ADC=∠AOC=25°.
二、填空题
11.
58°
提示:
根据圆周角定理求∠AOC的度数,再由等腰三角形的性质求出∠OAC的度数.
12.
4﹣.
13.
75°或15°.
提示:连接OA,过O作OE⊥AB于E,OF⊥AC于F,根据垂径定理求出AE、FA值,根据解直角三角形的知识求出∠OAB和∠OAC,然后分两种情况求出∠BAC即可.
14.
90°
提示:连接OB、OD,根据圆内接四边形的性质,得∠DCB=50°,根据圆周角定理,得
∠DOB=100°,于是50°<∠BPD<100°.
15.
2+或2-
提示:分外心在等腰三角形的内部和外部两种情形求解.
16.
π
提示:如图点P运动的路径是以G为圆心的弧,在⊙G上取一点D,连接ED、FD.
由∠AOC=90°,知道∠AFP=45°,由EF是⊙O直径,所以∠EAF=90°,
所以∠APF=∠AFP=45°,由圆的内接四边形互补,得∠D=∠APF=45°,
所以∠EGF=90°,因为EF=4,GE=GF,所以三角形EGF是等腰直角三角形,
所以EG=GF=2,所以的长==π.
三、解答题
17.略
18.
解:(1)因为三角形ABC的面积是定值,所以CD=.易证△ADC∽△ACB,
所以AD=,因为⊙是三角形ACD的内切圆,半径为,所以AD-+CD-=AC
所以==;
同理可证,
=;
(2)因为=,=,所以=.
19.
证明:
(1)因为∠A=30°,所以∠DCB=30°,因为AB为⊙O的直径,AB⊥弦CD,
所以∠BGC=90°,所以∠OBC=60°,因为AB为⊙O的直径,EF切⊙O于点B,
所以∠ABE=90°,所以∠EBC=30°;
(2)因为∠OBC=60°,OB=OC,所以三角形OBC是等边三角形,
所以弧BC的长度为
=π.
20.
解:(1)因为BC=5,AC=6,AB=9,
所以p==10,
所以S===10,
所以△ABC的面积10;
(2)因为S=r(AC+BC+AB),
所以10=r(5+6+9),解得:r=,
所以△ABC的内切圆半径r=.
21.
解
(1)证明:如图连接OD.因为四边形OBEC是平行四边形,
所以OC∥BE,所以∠AOC=∠OBE,∠COD=∠ODB,
因为OB=OD,所以∠OBD=∠ODB,所以∠DOC=∠AOC,
在△COD和△COA中,,所以△COD≌△COA,
所以∠CAO=∠CDO=90°,所以CF⊥OD,
所以CF是⊙O的切线.
(2)解:因为∠F=30°,∠ODF=90°,
所以∠DOF=∠AOC=∠COD=60°,因为OD=OB,所以△OBD是等边三角形,
所以∠DBO=60°,因为∠DBO=∠F+∠FDB,
所以∠FDB=∠EDC=30°,因为EC∥OB,
所以∠E=180°﹣∠OBD=120°,所以∠ECD=180°﹣∠E﹣∠EDC=30°,
所以EC=ED=BO=DB,因为EB=4,
所以OB=OD═OA=2,
在RT△AOC中,因为∠OAC=90°,OA=2,∠AOC=60°,
所以AC=OA?tan60°=2,
所以S阴=2?S△AOC﹣S扇形OAD=2××2×2﹣=2﹣.
22.
解:(1)因为点E是直角三角形ABC斜边AB的中点,∠A=30°,
所以三角形BEC是等边三角形,因为点D是三角形ABC的内心,
连接BD,则DB平分∠ABC,所以直线BD是线段EC的垂直平分线,所以DE=DC;
(2)因为DC平分∠ACB,所以∠BCD=45°,因为∠BCE=60°,所以∠DEC=15°.
23.
解:(1)证明:如图1,连结CO.因为AB=6,BC=8,∠B=90°,
所以AC=10.因为CD=24,AD=26,且,
所以△ACD是直角三角形,∠C=90°.因为AD为⊙O的直径,所以AO=OD=13,
因为OC为Rt△ACD斜边上的中线,所以OC=AD=13,所以点C在圆O上;
(2)解:如图2,延长BC、DE交于点F,因为∠B=90°,DE∥AB,所以∠BFD=90°.
所以∠CDE+∠FCD=90°,因为AD为直径,所以∠ACD=90°,
所以∠ACB+∠FCD=90°,所以∠CDE=∠ACB.
在Rt△ABC中,tan∠ACB==,所以tan∠CDE=tan∠ACB=;
(3)解:如图3,连结AE,作OG⊥ED于点G,因为AD为直径,所以AE⊥ED
所以OG∥AE,GD=GE,所以OG是三角形AED的中位线,所以OG=AE.
因为sin∠CDF=sin∠ACB=,所以CF=CDsin∠CDF=,所以BF=BC+CF=8+=.
易证四边形ABFE是矩形,所以AE=BF=,
所以OG=AE=,即圆心O到弦ED的距离为.
24.
解:
发现:如图1,连接OP,OQ,则三角形POQ是等边三角形,所以∠POQ=60°,
所以∠AOP+∠BOQ=120°,因为二弧是在同圆中,所以m==;
思考:当AB∥PQ时,距离最大,如图2所示,因为三角形POQ是等边三角形,OM⊥PQ,
所以OM==,此时三角形AOP也是等边三角形,所以PA=2;
当点Q与点B重合时,距离最短,PQ是直径,所以PH⊥AB,由三角形POB是等边三角形,
所以PH=,
MT⊥OB,所以TH=TB,所以TM是三角形BHP的中位线,所以TM=;
连接MH,三角形HBM是边长为1的等边三角形,所以==,
等边三角形HBM的面积为
=,所以围成的封闭图形的面积为:-.
探究:半圆M与AB相切,分两种情况:
①如图4,半圆M与AO切于点T时,连结PO,MO,TM.
则MT⊥AO,OM⊥PQ,在Rt△POM中,sin∠POM=,
所以∠POM=30°,在Rt△TOM中,TO=,
所以cos∠AOM=,即∠AOM=35°,所以∠POA=35°-30°=5°.
所以弧AP的长=.
②如图5,半圆M与BO切于点S时,连结PO,MO,SM.
根据圆的对称性,同理得弧BQ的长为,由得弧AP的长为.
综上所述,弧AP的长为.
时间:100分钟
满分:120分
姓名:
一、选择题(每小题3分,共30分)
1.在公园的O处附近有E、F、G、H四棵树,位置如图1所示(图中小正方形的边长均相等),现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E、F、G、H四棵树中需要被移除的为
( )
(A)E、F、G.
(B)F、G、H.
(C)G、H、E.
(D)H、E、F.
图
1
2.下列图形中,不是中心对称图形的是
( )
3.如图2,CD是⊙O的直径,弦AB⊥CD于E,连接BC、BD,下列结论中不一定正确的是
( )
(A)AE=BE.
(B)=.
(C)OE=DE.
(D)∠DBC=90°.
图
2
4.如图3,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于
(
)
(A)12.5°.
(B)15°.
(C)20°.
(D)22.5°
图
3
5.下列条件,四边形ABCD一定有外接圆的是
( )
(A)∠A:∠B:∠C:∠D=1:3:3:4.
(B)∠A:∠B:∠C:∠D=2:3:3:5.
(C)∠A:∠B:∠C:∠D=2:3:3:5.
(D)∠A:∠B:∠C:∠D=2:3:3:2.
6.如图4,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则的长为
( )
(A)π.
(B)6π.
(C)3π.
(D)1.5π.
图
4
7.如图5,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是
( )
(A)25°.
(B)40°.
(C)50°.
(D)65°.
图
5
8.如图6示为4×4的网格图,A,B,C,D,O均在格点上,点O是
(
)
(A)△ACD的外心.
(B)△ABC的外心.
(C)△ACD的内心.
(D)△ABC的内心.
图
6
9.如图7,已知同心圆O,点P是大圆上一个定点,点A是小圆上的一个动点,连接PA,设PA的最大值为a,最小值为b,若大圆的半径为6,小圆的半径的2,则a+b的值为
( )
(A)9.
(B)10.
(C)12.
(D)14.
图
7
10.如图8,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是优弧上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=80°,则∠ADC的度数是
( )
(A)15°.
(B)20°.
(C)25°.
(D)30°.
图
8
二、填空题(每小题4分,共24分)
11.
如图9,A、D是⊙O上的两个点,BC是直径.若∠D=32°,则∠OAC=
.
图
9
12.如图10,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE=
.
图
10
13.
⊙O的半径为1,弦AB=,弦AC=,那么∠BAC度数
为
.
14.如图11,四边形ABCD内接于⊙O,∠DAB=130°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为
度(写出一个即可).
图
11
15.若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=2,则△ABC的
面积为
.
16.
如图12,正方形OABC的边长为2,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是 .
图
12
三、解答题(共66分)
17.(满分5分)有一块三角形废铁板,为节约材料,厂家决定变废为宝,技术革新,可以把它变成一个圆形的炉口,请你帮厂家拿出一个最大利用的方案.
18.
(满分8分)如图13,CD是Rt△ABC斜边AB上高,⊙是三角形ACD的内切圆,半径为,⊙是三角形BCD的内切圆,半径为,设三角形ABC的三边长分别为a,b,c.
(1)用a,b,c分别表示,;
(2)计算的值.
图
13
19.
(满分8分)如图14,AB为⊙O的直径,AB=6,AB⊥弦CD,垂足为G,EF切⊙O于点B,∠A=30°,
连接AD、OC、BC,求证:(1)∠EBC=30°;(2)求弧BC的长度.
图
14
20.
(满分8分)已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=,其中a,b,c是三角形的三边长,p=,S是三角形的面积,并给出了证明.
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
因为a=3,b=4,c=5
所以p==6
所以S===6
事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
如图15,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
图
15
21.
(满分8分)如图16,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根号和π)
图
16
22.
(满分8分)如图17所示,点E是直角三角形ABC斜边AB的中点,点D是三角形ABC的内心,且∠A=30°.
(1)求证:DE=DC;
(2)求∠DEC的度数.
图
17
23.
(满分9分)如图18,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,过点D作DE∥AB交圆O于点E
(1)证明点C在圆O上;(2)求tan∠CDE的值;
(3)求圆心O到弦ED的距离.
图
18
24.
(满分12分)如图19,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M,其中P点在AQ(弧)上且不与A点重合,但Q点可与B点重合.
发现
AP(弧)的长与QB(弧)的长之和为定值m,求m;
思考
点M与AB的最大距离为_______,此时点P,A间的距离为_______;
点M与AB的最小距离为________,此时半圆M的弧与AB所围成的封闭图形面积
为________.
探究
当半圆M与AB相切时,求AP(弧)的长.
(注:结果保留π,cos
35°=,cos
55°=)
图
19
参考答案:
直线与圆的位置关系测试题
一、选择题
1.(A)
提示:OA=,则OE=2<OA,点E在⊙O内,OF=2<OA,点F在⊙O内,OG=1<OA,点G在⊙O内,OH=>OA,点H在⊙O外.
2.(B)
提示:旋转180度后仍能与原来图形重合的图形是中心对称图形.
3.(C)
提示:根据垂径定理去一一判定,只有C是没有条件支撑.
4.
(B)
提示:
连接OB,因为四边形ABCO是平行四边形,OA=OC,所以四边形ABCO是菱形.
所以△AOB为等边三角形,因为OF⊥OC,OC∥AB,所以OF⊥AB,
所以∠BOF=∠AOF=30°,由圆周角定理得∠BAF=∠BOF=15°.
5.(D)
提示:
圆的内接四边形对角互补,所以对角和所占比数和相等.
6.
(D)
提示:所在扇形是扇形AOB,其半径是OA,其圆心角是∠AOB,半径OA=3,旋转角度为90°,所以∠AOB=90°,所以的长为:=1.5π.
7.
(B)
提示:
连接OC,由∠A=25°,可求得∠BOC的度数,由CD是圆O的切线,可得OC⊥CD,继而求得答案.
8.(B)
提示:计算O到A,B,C,D的距离,OA=OB=OC,根据定义知点O是三角形ABC的外心.
9.
(C)
提示:当P,O,A共线时,PA与小圆的有两个交点,远离P的那个交点,PA最大,此时a=6+2=8;
靠近P的交点,PA值最小,此时b=6-2=4,所以a+b=12.
10.
(C)
提示:由切线性质,得
∠BOA=360°﹣90°﹣90°﹣80°=100°,
由=,得∠AOC=∠BOC=50°.由圆周角定理,得∠ADC=∠AOC=25°.
二、填空题
11.
58°
提示:
根据圆周角定理求∠AOC的度数,再由等腰三角形的性质求出∠OAC的度数.
12.
4﹣.
13.
75°或15°.
提示:连接OA,过O作OE⊥AB于E,OF⊥AC于F,根据垂径定理求出AE、FA值,根据解直角三角形的知识求出∠OAB和∠OAC,然后分两种情况求出∠BAC即可.
14.
90°
提示:连接OB、OD,根据圆内接四边形的性质,得∠DCB=50°,根据圆周角定理,得
∠DOB=100°,于是50°<∠BPD<100°.
15.
2+或2-
提示:分外心在等腰三角形的内部和外部两种情形求解.
16.
π
提示:如图点P运动的路径是以G为圆心的弧,在⊙G上取一点D,连接ED、FD.
由∠AOC=90°,知道∠AFP=45°,由EF是⊙O直径,所以∠EAF=90°,
所以∠APF=∠AFP=45°,由圆的内接四边形互补,得∠D=∠APF=45°,
所以∠EGF=90°,因为EF=4,GE=GF,所以三角形EGF是等腰直角三角形,
所以EG=GF=2,所以的长==π.
三、解答题
17.略
18.
解:(1)因为三角形ABC的面积是定值,所以CD=.易证△ADC∽△ACB,
所以AD=,因为⊙是三角形ACD的内切圆,半径为,所以AD-+CD-=AC
所以==;
同理可证,
=;
(2)因为=,=,所以=.
19.
证明:
(1)因为∠A=30°,所以∠DCB=30°,因为AB为⊙O的直径,AB⊥弦CD,
所以∠BGC=90°,所以∠OBC=60°,因为AB为⊙O的直径,EF切⊙O于点B,
所以∠ABE=90°,所以∠EBC=30°;
(2)因为∠OBC=60°,OB=OC,所以三角形OBC是等边三角形,
所以弧BC的长度为
=π.
20.
解:(1)因为BC=5,AC=6,AB=9,
所以p==10,
所以S===10,
所以△ABC的面积10;
(2)因为S=r(AC+BC+AB),
所以10=r(5+6+9),解得:r=,
所以△ABC的内切圆半径r=.
21.
解
(1)证明:如图连接OD.因为四边形OBEC是平行四边形,
所以OC∥BE,所以∠AOC=∠OBE,∠COD=∠ODB,
因为OB=OD,所以∠OBD=∠ODB,所以∠DOC=∠AOC,
在△COD和△COA中,,所以△COD≌△COA,
所以∠CAO=∠CDO=90°,所以CF⊥OD,
所以CF是⊙O的切线.
(2)解:因为∠F=30°,∠ODF=90°,
所以∠DOF=∠AOC=∠COD=60°,因为OD=OB,所以△OBD是等边三角形,
所以∠DBO=60°,因为∠DBO=∠F+∠FDB,
所以∠FDB=∠EDC=30°,因为EC∥OB,
所以∠E=180°﹣∠OBD=120°,所以∠ECD=180°﹣∠E﹣∠EDC=30°,
所以EC=ED=BO=DB,因为EB=4,
所以OB=OD═OA=2,
在RT△AOC中,因为∠OAC=90°,OA=2,∠AOC=60°,
所以AC=OA?tan60°=2,
所以S阴=2?S△AOC﹣S扇形OAD=2××2×2﹣=2﹣.
22.
解:(1)因为点E是直角三角形ABC斜边AB的中点,∠A=30°,
所以三角形BEC是等边三角形,因为点D是三角形ABC的内心,
连接BD,则DB平分∠ABC,所以直线BD是线段EC的垂直平分线,所以DE=DC;
(2)因为DC平分∠ACB,所以∠BCD=45°,因为∠BCE=60°,所以∠DEC=15°.
23.
解:(1)证明:如图1,连结CO.因为AB=6,BC=8,∠B=90°,
所以AC=10.因为CD=24,AD=26,且,
所以△ACD是直角三角形,∠C=90°.因为AD为⊙O的直径,所以AO=OD=13,
因为OC为Rt△ACD斜边上的中线,所以OC=AD=13,所以点C在圆O上;
(2)解:如图2,延长BC、DE交于点F,因为∠B=90°,DE∥AB,所以∠BFD=90°.
所以∠CDE+∠FCD=90°,因为AD为直径,所以∠ACD=90°,
所以∠ACB+∠FCD=90°,所以∠CDE=∠ACB.
在Rt△ABC中,tan∠ACB==,所以tan∠CDE=tan∠ACB=;
(3)解:如图3,连结AE,作OG⊥ED于点G,因为AD为直径,所以AE⊥ED
所以OG∥AE,GD=GE,所以OG是三角形AED的中位线,所以OG=AE.
因为sin∠CDF=sin∠ACB=,所以CF=CDsin∠CDF=,所以BF=BC+CF=8+=.
易证四边形ABFE是矩形,所以AE=BF=,
所以OG=AE=,即圆心O到弦ED的距离为.
24.
解:
发现:如图1,连接OP,OQ,则三角形POQ是等边三角形,所以∠POQ=60°,
所以∠AOP+∠BOQ=120°,因为二弧是在同圆中,所以m==;
思考:当AB∥PQ时,距离最大,如图2所示,因为三角形POQ是等边三角形,OM⊥PQ,
所以OM==,此时三角形AOP也是等边三角形,所以PA=2;
当点Q与点B重合时,距离最短,PQ是直径,所以PH⊥AB,由三角形POB是等边三角形,
所以PH=,
MT⊥OB,所以TH=TB,所以TM是三角形BHP的中位线,所以TM=;
连接MH,三角形HBM是边长为1的等边三角形,所以==,
等边三角形HBM的面积为
=,所以围成的封闭图形的面积为:-.
探究:半圆M与AB相切,分两种情况:
①如图4,半圆M与AO切于点T时,连结PO,MO,TM.
则MT⊥AO,OM⊥PQ,在Rt△POM中,sin∠POM=,
所以∠POM=30°,在Rt△TOM中,TO=,
所以cos∠AOM=,即∠AOM=35°,所以∠POA=35°-30°=5°.
所以弧AP的长=.
②如图5,半圆M与BO切于点S时,连结PO,MO,SM.
根据圆的对称性,同理得弧BQ的长为,由得弧AP的长为.
综上所述,弧AP的长为.
同课章节目录
