广西南宁市银海三美学校2020-2021学年高一第一学期段考数学试卷(图片版含答案解析)
文档属性
| 名称 | 广西南宁市银海三美学校2020-2021学年高一第一学期段考数学试卷(图片版含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-15 16:18:14 | ||
图片预览



文档简介
已知函数∫(x)=x5
若∫(-3)=10,则f(3)
A.-26
B.26
C.18
10.已知集合A=(xx<3),B={xx>a,若A∩B≠0,则实数a的取值范围为(
A.[3,+∞)
C.(
3)
ll.若
y
2mx+3是偶函数,则f(-1),f(V2,f(3的大小关系为(
A/((3)>f(2>>f
∫(√3<(-√2
C.
f(
≤(V3)12.设∫(x)为奇函数且在(-∞,0)内是减函数,∫(-2)=0,且x(x)>0的解集
为6
A.(-2,0)U(2,
2)U(0,2)
C.(
2)U(2,+∞)
D.(-2,0)U(0,2)
、填空罳(本大共4小题每5分,满分20分,将答案填在答题纸上)
3.已知映射Fx→y由表给出,则f(2
23
3
2
14.分解因式:22-8
5.函数f(x)=3+2x的定义域为
16.已知函数∫(x)=
2-4+6x20,则不等式f(x)>f()的解集是一
x+6,x<0
、解答〔共70分。解谷应写出文字说明、证明过程成演算步聊。)
17没全集U={0,1,2,3,4,5,6,7,8,9,10},M={2,4,6
8},A={1,3,5,
7],B={5,10},求MnA,(MUB)∩A,Cu(AUB)
第2页
18.已知全集U=R,集合A={x1-1(1)A∩B;(2)cu(AUB);(3)A∩(CUB)
9.(1)计算:2163+(4)
+Jt
125
化简(ab4)
)°÷(ab)
(a>0,b>0);
(3)已知x
求
的值
xy《xy
20.已知函数f(x)
x-1,
xE(2,
(1)用定义证明∫(x)在定义域内是单调递减函数;
(2)求该函数的值域
第3页
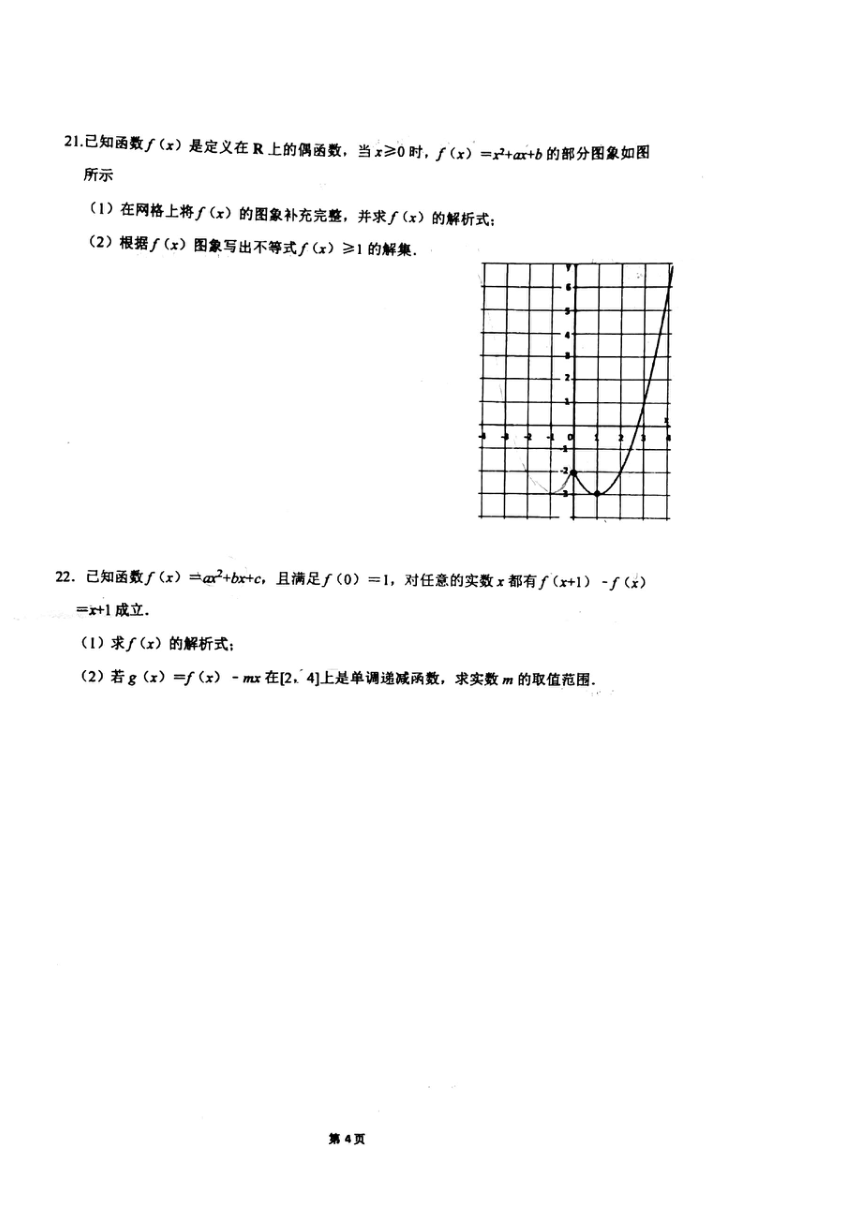
21已知函数∫(x)是定义在R上的偶函数,当x≥0时,f(x)=x2+ax+b的部分图象如图
所示
(1)在网格上将∫(x)的图象补充完整,并求∫(x)的解析式
(2)根据∫(x)图象写出不等式∫(x)≥1的解集
十十
22.已知函数∫(x)=a2+bx+c,且满足f(0)=1,对任意的实数x都有∫(x+1)-f(x)
=x+1成立
(1)求∫(x)的解析式;
(2)若g(x)=f(x)-mx在2,4]上是单调递减函数,求实数m的取值范围
第4页
高一段考数学试题答案
选择题
1解:∵M={-2,0,1},N={-1,0,2},
∴MnN={0}.故选:A
2解:函数表示每个输入值对应唯一输出值的一种对应关系
对B中图象,对于x>0的x值,有两个输出值与之对应,故不是函数图象。故选:B
3解:∵函数∫(x)
x-2,x<2
x(x-2),x>2
∴(4)=4×(4-2)=8.故选:C
4解:根据题意,依次分析选项:
对于A,y=x2,是对称轴为y轴的二次函数,是偶函数,不符合题意,
对于B,f(x)=x3,是幂函数,是奇函数但在R上是增函数,不符合题意,
对于C,f(x)=,是反比例函数,是奇函数但在其定义域上不是减函数,需分开区间来说,不
符合题意,对于D,y=-x,是正比例函数,既是奇函数又是减函数,符合题意。故选:D
5解:集合{x2-1=0}={1,-1},它的真子集为团,{},{-1}.共3个真子集
故选:B
6解:∵全集U=R,集合A={0,1,2,3,4},B={xx>2或x<0},
∴图中阴影部分表示的集合为
A∩(区UB)={0,1,2,3,4}n∩{x0≤x≤2}={0,1,2}.故选:A.
7解:∵关于x的一元二次方程k2-x+1=0有实数根,∴k≠0且△=(-1)2-4≥0,
解得:长≤与且k≠0.故选:C.
8解:f
x-2)=4(x-2)+14,∴∫(x)=4x+14.故选:B
9解:令g(x)=x5+a3+bx,由函数奇偶性的定义,易得其为奇函数
则f(x)=g(x)-8,所以∫(-3)=g(-3)-8
得g(-3)=18,又因为g(x)是奇函数,即g(3)
(-3)
所以g(3)=-18,则∫(3)=g(3)-8=-26.故选:A
10.解:结合数轴可知,当a≥3时,A∩B=园,
故A∩B≠园,则实数a的取值范围a<3,
第页
若∫(-3)=10,则f(3)
A.-26
B.26
C.18
10.已知集合A=(xx<3),B={xx>a,若A∩B≠0,则实数a的取值范围为(
A.[3,+∞)
C.(
3)
ll.若
y
2mx+3是偶函数,则f(-1),f(V2,f(3的大小关系为(
A/((3)>f(2>>f
∫(√3<(-√2
C.
f(
≤(V3)
为6
A.(-2,0)U(2,
2)U(0,2)
C.(
2)U(2,+∞)
D.(-2,0)U(0,2)
、填空罳(本大共4小题每5分,满分20分,将答案填在答题纸上)
3.已知映射Fx→y由表给出,则f(2
23
3
2
14.分解因式:22-8
5.函数f(x)=3+2x的定义域为
16.已知函数∫(x)=
2-4+6x20,则不等式f(x)>f()的解集是一
x+6,x<0
、解答〔共70分。解谷应写出文字说明、证明过程成演算步聊。)
17没全集U={0,1,2,3,4,5,6,7,8,9,10},M={2,4,6
8},A={1,3,5,
7],B={5,10},求MnA,(MUB)∩A,Cu(AUB)
第2页
18.已知全集U=R,集合A={x1-1
9.(1)计算:2163+(4)
+Jt
125
化简(ab4)
)°÷(ab)
(a>0,b>0);
(3)已知x
求
的值
xy《xy
20.已知函数f(x)
x-1,
xE(2,
(1)用定义证明∫(x)在定义域内是单调递减函数;
(2)求该函数的值域
第3页
21已知函数∫(x)是定义在R上的偶函数,当x≥0时,f(x)=x2+ax+b的部分图象如图
所示
(1)在网格上将∫(x)的图象补充完整,并求∫(x)的解析式
(2)根据∫(x)图象写出不等式∫(x)≥1的解集
十十
22.已知函数∫(x)=a2+bx+c,且满足f(0)=1,对任意的实数x都有∫(x+1)-f(x)
=x+1成立
(1)求∫(x)的解析式;
(2)若g(x)=f(x)-mx在2,4]上是单调递减函数,求实数m的取值范围
第4页
高一段考数学试题答案
选择题
1解:∵M={-2,0,1},N={-1,0,2},
∴MnN={0}.故选:A
2解:函数表示每个输入值对应唯一输出值的一种对应关系
对B中图象,对于x>0的x值,有两个输出值与之对应,故不是函数图象。故选:B
3解:∵函数∫(x)
x-2,x<2
x(x-2),x>2
∴(4)=4×(4-2)=8.故选:C
4解:根据题意,依次分析选项:
对于A,y=x2,是对称轴为y轴的二次函数,是偶函数,不符合题意,
对于B,f(x)=x3,是幂函数,是奇函数但在R上是增函数,不符合题意,
对于C,f(x)=,是反比例函数,是奇函数但在其定义域上不是减函数,需分开区间来说,不
符合题意,对于D,y=-x,是正比例函数,既是奇函数又是减函数,符合题意。故选:D
5解:集合{x2-1=0}={1,-1},它的真子集为团,{},{-1}.共3个真子集
故选:B
6解:∵全集U=R,集合A={0,1,2,3,4},B={xx>2或x<0},
∴图中阴影部分表示的集合为
A∩(区UB)={0,1,2,3,4}n∩{x0≤x≤2}={0,1,2}.故选:A.
7解:∵关于x的一元二次方程k2-x+1=0有实数根,∴k≠0且△=(-1)2-4≥0,
解得:长≤与且k≠0.故选:C.
8解:f
x-2)=4(x-2)+14,∴∫(x)=4x+14.故选:B
9解:令g(x)=x5+a3+bx,由函数奇偶性的定义,易得其为奇函数
则f(x)=g(x)-8,所以∫(-3)=g(-3)-8
得g(-3)=18,又因为g(x)是奇函数,即g(3)
(-3)
所以g(3)=-18,则∫(3)=g(3)-8=-26.故选:A
10.解:结合数轴可知,当a≥3时,A∩B=园,
故A∩B≠园,则实数a的取值范围a<3,
第页
同课章节目录
