人教版数学八年级上册《12.3 角平分线的性质》同步练习卷(Word版 含答案)
文档属性
| 名称 | 人教版数学八年级上册《12.3 角平分线的性质》同步练习卷(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 128.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-15 15:41:20 | ||
图片预览



文档简介
《12.3 角平分线的性质》同步练习卷
一.选择题
1.利用尺规作∠AOB的角平分线OC的作图痕迹如图所示,说明∠AOC=∠BOC用到的三角形全等的判定方法是( )
A.SSS B.SAS C.ASA D.AAS
2.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.3 B.4 C.5 D.6
3.如图,已知P是∠AOB的角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,点C是OB上的一个动点,若PC的最小值为3cm,则MD的长度为( )
A.3cm B.3cm C.2cm D.2cm
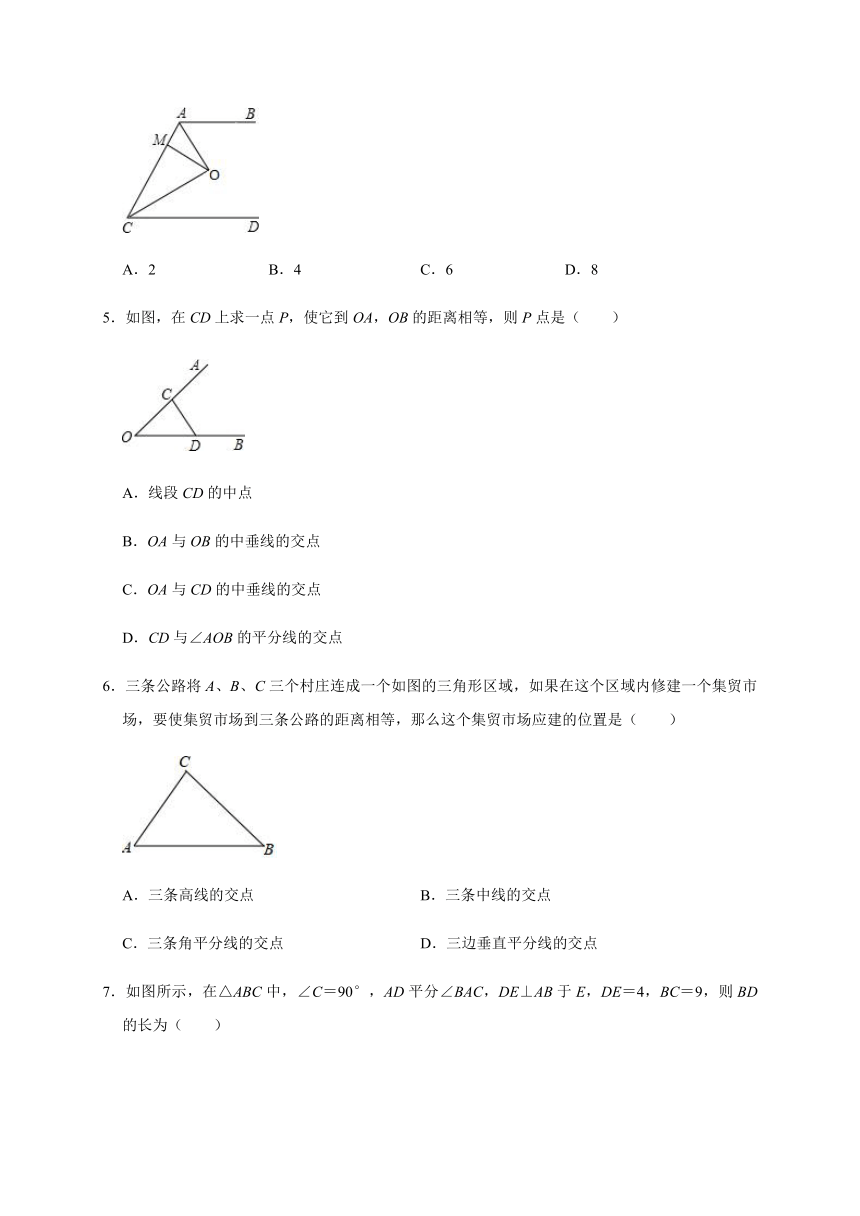
4.如图,已知AB∥CD,OA、OC分别平分∠BAC和∠ACD,OM⊥AC于点M,且OM=3,则AB、CD之间的距离为( )
A.2 B.4 C.6 D.8
5.如图,在CD上求一点P,使它到OA,OB的距离相等,则P点是( )
A.线段CD的中点
B.OA与OB的中垂线的交点
C.OA与CD的中垂线的交点
D.CD与∠AOB的平分线的交点
6.三条公路将A、B、C三个村庄连成一个如图的三角形区域,如果在这个区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,那么这个集贸市场应建的位置是( )
A.三条高线的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
7.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为( )
A.6 B.5 C.4 D.3
二.填空题
8.如图,△ABC的三边AB,BC,CA的长分别为30,40,15,点P是△ABC三个内角平分线的交点,则S△PAB:S△PBC:S△PCA= .
9.如图,△ABC中,AB=8,BC=10,BD是△ABC的角平分线,DE⊥AB于点E,若DE=4,则三角形ABC的面积为 .
10.如图,平面直角坐标系中,AD平分∠BAC,D(4,0),AB=10,则△ABD的面积是 .
三.解答题
11.作图题:
如图,已知点A,点B,直线l及l上一点M.
(1)连接MA,并在直线l上作出一点N,使得点N在点M的左边,且满足MN=MA;
(2)请在直线l上确定一点O,使点O到点A与点O到点B的距离之和最短,并写出画图的依据.
12.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.求证:AD是△ABC的角平分线.
13.两组邻边分别相等的四边形我们称它为筝形.如图,在筝形ABCD中,AB=AD,BC=DC,AC、BD相交于点O,求证:
(1)△ABC≌△ADC;
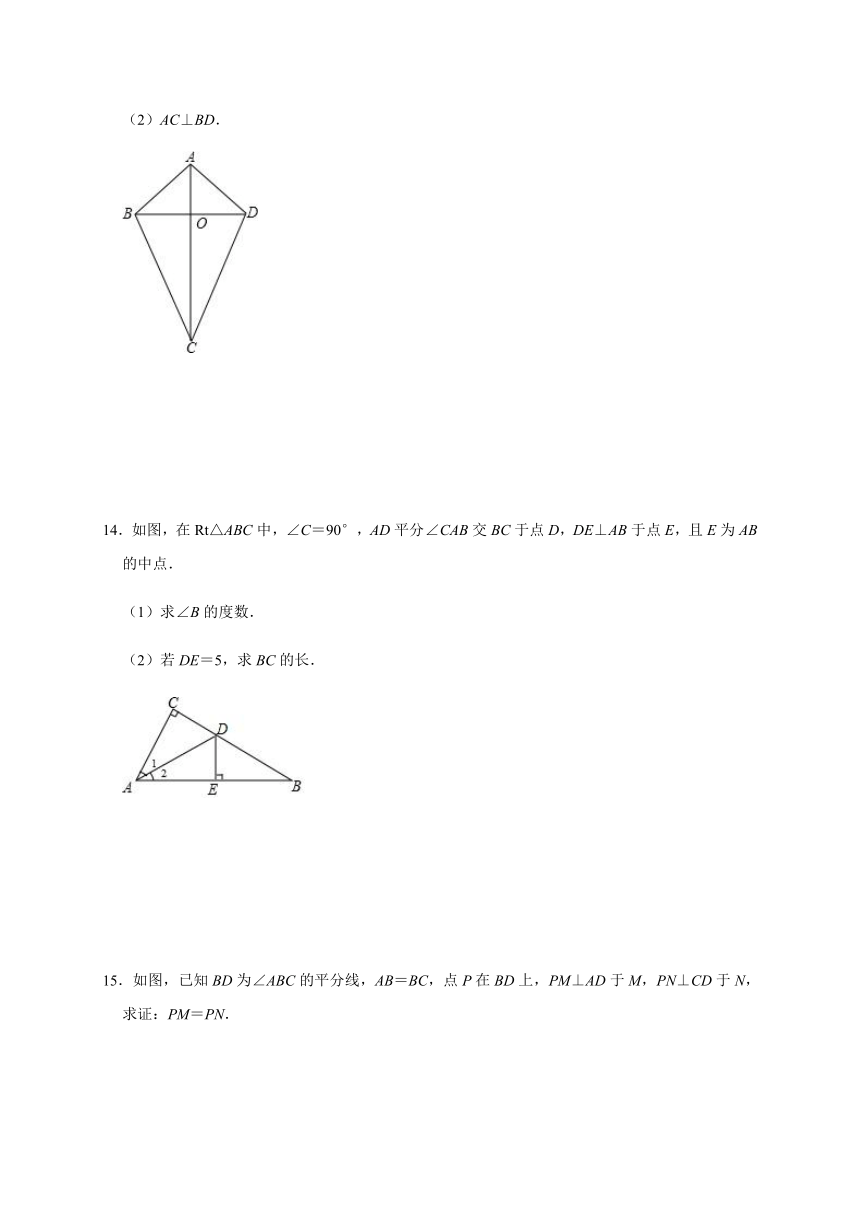
(2)AC⊥BD.
14.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E,且E为AB的中点.
(1)求∠B的度数.
(2)若DE=5,求BC的长.
15.如图,已知BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.
参考答案
一.选择题
1.解:如图,连接CD,CE,
由作法可知OE=OD,CE=CD,OC=OC,
故可得出△OCE≌△OCD(SSS),
所以∠AOC=∠BOC,
所以OC就是∠AOB的平分线.
故选:A.
2.解:如图,过点D作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC,
∴DE=CD,
∴S△ABD=AB?DE=×10?DE=15,
解得DE=3,
∴CD=3.
故选:A.
3.解:作PC⊥OB于C,则此时PC最小,
∵P是∠AOB的角平分线上的一点,PD⊥OA,PC⊥OB,
∴PD=PC=3,∠AOP=30°,
∴OP=2PD=6,
∵PD⊥OA,M是OP的中点,
∴DM=OP=3,
故选:A.
4.解:作OF⊥AB,延长FO与CD交于G点,
∵AB∥CD,
∴FG垂直CD,
∴FG就是AB与CD之间的距离.
∵∠ACD平分线的交点,OE⊥AC交AC于M,
∴OM=OF=OG,
∴AB与CD之间的距离等于2OM=6.
故选:C.
5.解:利用角的平分线上的点到角的两边的距离相等可知CD与∠AOB的平分线的交于点P.
故选:D.
6.解:在这个区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,
根据角平分线的性质,集贸市场应建在∠A、∠B、∠C的角平分线的交点处.
故选:C.
7.解:∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DC=DE=4,
∴BD=BC﹣CD=9﹣4=5.
故选:B.
二.填空题
8.解:∵点P是△ABC三个内角平分线的交点,
∴P点到三边的距离相等,
设这个距离为m,
∴S△PAB:S△PBC:S△PCA=×AB×m:×BC×m:×AC×m
=AB:BC:AC
=30:40:15
=6:8:3.
故答案为6:8:3.
9.解:过D作DF⊥BC,
∵BD是△ABC的角平分线,DE⊥AB于点E,DE=4,
∴DF=4,
∴△ABC的面积=△ABD的面积+△DBC的面积=,
故答案为:36
10.解:如图,作DH⊥AB于H.
∵AD平分∠BAC,DC⊥AC,DH⊥AB,
∴DC=DH=4,
∴S△ABD=?AB?DH=×10×4=20.
故答案为20.
三.解答题
11.解:(1)作图如图1所示:
(2)作图如图2所示:作图依据是:两点之间线段最短.
12.证明:∵DE⊥AB,DF⊥AC,
∴Rt△BDE和Rt△CDF是直角三角形.
,
∴Rt△BDE≌Rt△CDF(HL),
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴AD是角平分线.
13.证明:(1)在△ABC和△ADC中
,
∴△ABC≌△ADC(SSS);
(2)∵△ABC≌△ADC,
∴∠BAC=∠DAC,
∵AB=AD,
∴AO垂直平分BD,
∴AC⊥BD.
14.解:(1)∵DE⊥AB于点E,E为AB的中点,
∴DE是线段AB的垂直平分线,
∴DA=DB,
∴∠2=∠B,
∵∠C=90°,
∴∠B=∠1=∠2=30°;
(2)∵DE⊥AB,∠B=30°,
∴BD=2DE=10,
∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴DC=DE=5,
∴BC=CD+BD=15.
15.证明:∵BD为∠ABC的平分线,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,
∵点P在BD上,PM⊥AD,PN⊥CD,
∴PM=PN.
一.选择题
1.利用尺规作∠AOB的角平分线OC的作图痕迹如图所示,说明∠AOC=∠BOC用到的三角形全等的判定方法是( )
A.SSS B.SAS C.ASA D.AAS
2.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.3 B.4 C.5 D.6
3.如图,已知P是∠AOB的角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,点C是OB上的一个动点,若PC的最小值为3cm,则MD的长度为( )
A.3cm B.3cm C.2cm D.2cm
4.如图,已知AB∥CD,OA、OC分别平分∠BAC和∠ACD,OM⊥AC于点M,且OM=3,则AB、CD之间的距离为( )
A.2 B.4 C.6 D.8
5.如图,在CD上求一点P,使它到OA,OB的距离相等,则P点是( )
A.线段CD的中点
B.OA与OB的中垂线的交点
C.OA与CD的中垂线的交点
D.CD与∠AOB的平分线的交点
6.三条公路将A、B、C三个村庄连成一个如图的三角形区域,如果在这个区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,那么这个集贸市场应建的位置是( )
A.三条高线的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
7.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为( )
A.6 B.5 C.4 D.3
二.填空题
8.如图,△ABC的三边AB,BC,CA的长分别为30,40,15,点P是△ABC三个内角平分线的交点,则S△PAB:S△PBC:S△PCA= .
9.如图,△ABC中,AB=8,BC=10,BD是△ABC的角平分线,DE⊥AB于点E,若DE=4,则三角形ABC的面积为 .
10.如图,平面直角坐标系中,AD平分∠BAC,D(4,0),AB=10,则△ABD的面积是 .
三.解答题
11.作图题:
如图,已知点A,点B,直线l及l上一点M.
(1)连接MA,并在直线l上作出一点N,使得点N在点M的左边,且满足MN=MA;
(2)请在直线l上确定一点O,使点O到点A与点O到点B的距离之和最短,并写出画图的依据.
12.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.求证:AD是△ABC的角平分线.
13.两组邻边分别相等的四边形我们称它为筝形.如图,在筝形ABCD中,AB=AD,BC=DC,AC、BD相交于点O,求证:
(1)△ABC≌△ADC;
(2)AC⊥BD.
14.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E,且E为AB的中点.
(1)求∠B的度数.
(2)若DE=5,求BC的长.
15.如图,已知BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.
参考答案
一.选择题
1.解:如图,连接CD,CE,
由作法可知OE=OD,CE=CD,OC=OC,
故可得出△OCE≌△OCD(SSS),
所以∠AOC=∠BOC,
所以OC就是∠AOB的平分线.
故选:A.
2.解:如图,过点D作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC,
∴DE=CD,
∴S△ABD=AB?DE=×10?DE=15,
解得DE=3,
∴CD=3.
故选:A.
3.解:作PC⊥OB于C,则此时PC最小,
∵P是∠AOB的角平分线上的一点,PD⊥OA,PC⊥OB,
∴PD=PC=3,∠AOP=30°,
∴OP=2PD=6,
∵PD⊥OA,M是OP的中点,
∴DM=OP=3,
故选:A.
4.解:作OF⊥AB,延长FO与CD交于G点,
∵AB∥CD,
∴FG垂直CD,
∴FG就是AB与CD之间的距离.
∵∠ACD平分线的交点,OE⊥AC交AC于M,
∴OM=OF=OG,
∴AB与CD之间的距离等于2OM=6.
故选:C.
5.解:利用角的平分线上的点到角的两边的距离相等可知CD与∠AOB的平分线的交于点P.
故选:D.
6.解:在这个区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,
根据角平分线的性质,集贸市场应建在∠A、∠B、∠C的角平分线的交点处.
故选:C.
7.解:∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DC=DE=4,
∴BD=BC﹣CD=9﹣4=5.
故选:B.
二.填空题
8.解:∵点P是△ABC三个内角平分线的交点,
∴P点到三边的距离相等,
设这个距离为m,
∴S△PAB:S△PBC:S△PCA=×AB×m:×BC×m:×AC×m
=AB:BC:AC
=30:40:15
=6:8:3.
故答案为6:8:3.
9.解:过D作DF⊥BC,
∵BD是△ABC的角平分线,DE⊥AB于点E,DE=4,
∴DF=4,
∴△ABC的面积=△ABD的面积+△DBC的面积=,
故答案为:36
10.解:如图,作DH⊥AB于H.
∵AD平分∠BAC,DC⊥AC,DH⊥AB,
∴DC=DH=4,
∴S△ABD=?AB?DH=×10×4=20.
故答案为20.
三.解答题
11.解:(1)作图如图1所示:
(2)作图如图2所示:作图依据是:两点之间线段最短.
12.证明:∵DE⊥AB,DF⊥AC,
∴Rt△BDE和Rt△CDF是直角三角形.
,
∴Rt△BDE≌Rt△CDF(HL),
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴AD是角平分线.
13.证明:(1)在△ABC和△ADC中
,
∴△ABC≌△ADC(SSS);
(2)∵△ABC≌△ADC,
∴∠BAC=∠DAC,
∵AB=AD,
∴AO垂直平分BD,
∴AC⊥BD.
14.解:(1)∵DE⊥AB于点E,E为AB的中点,
∴DE是线段AB的垂直平分线,
∴DA=DB,
∴∠2=∠B,
∵∠C=90°,
∴∠B=∠1=∠2=30°;
(2)∵DE⊥AB,∠B=30°,
∴BD=2DE=10,
∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴DC=DE=5,
∴BC=CD+BD=15.
15.证明:∵BD为∠ABC的平分线,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,
∵点P在BD上,PM⊥AD,PN⊥CD,
∴PM=PN.
