苏科版数学九年级下册5.4二次函数与一元二次方程课件(34张)
文档属性
| 名称 | 苏科版数学九年级下册5.4二次函数与一元二次方程课件(34张) |

|
|
| 格式 | zip | ||
| 文件大小 | 564.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-17 00:00:00 | ||
图片预览







文档简介
(共34张PPT)
二次函数与一元二次方程
第二章
二次函数
回顾旧知
二次函数的一般式:
(a≠0)
______是自变量,____是____的函数。
x
y
x
当
y
=
0
时,
ax?
+
bx
+
c
=
0
ax?
+
bx
+
c
=
0
这是什么方程?
九年级上册中我们学习了“一元二次方程”
一元二次方程与二次函数有什么关系?
教学目标
【知识与能力】
总结出二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系,表述何时方程有两个不等的实根、两个相等的实数和没有实根。
会利用二次函数的图象求一元二次方程的近似解。
通过观察二次函数图象与
x
轴的交点个数,讨论一元二次方程的根的情况,进一步体会数形结合思想。
【情感态度与价值观】
【过程与方法】
经历探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系。
教学重难点
二次函数与一元二次方程之间的关系。
利用二次函数图像求一元二次方程的实数根。
一元二次方程根的情况与二次函数图像与x轴位置关系的联系,数形结合思想的运用。
利用二次函数的图象求一元二次方程的近似解。
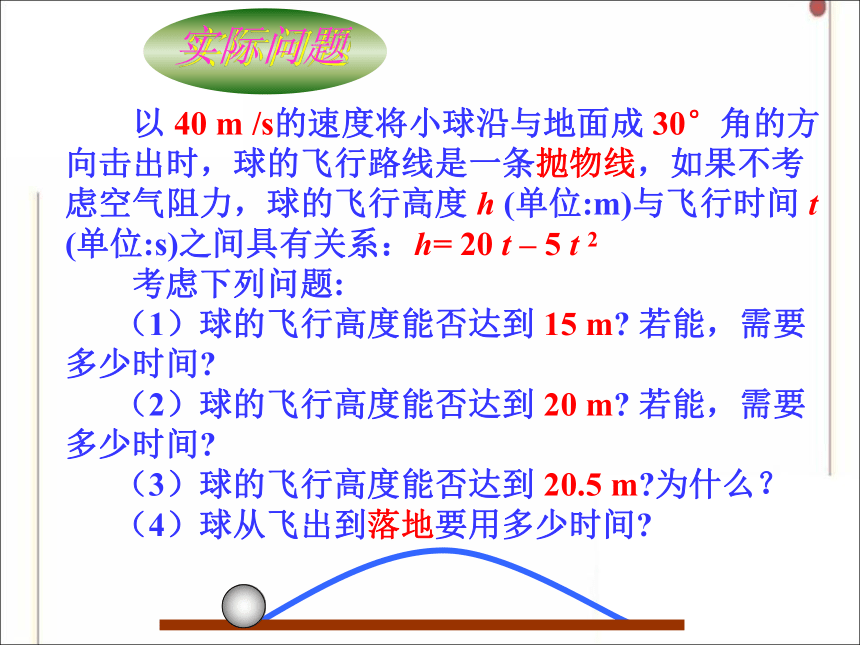
以
40
m
/s的速度将小球沿与地面成
30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度
h
(单位:m)与飞行时间
t
(单位:s)之间具有关系:h=
20
t
–
5
t
2
考虑下列问题:
(1)球的飞行高度能否达到
15
m?
若能,需要多少时间?
(2)球的飞行高度能否达到
20
m?
若能,需要多少时间?
(3)球的飞行高度能否达到
20.5
m?为什么?
(4)球从飞出到落地要用多少时间?
实际问题
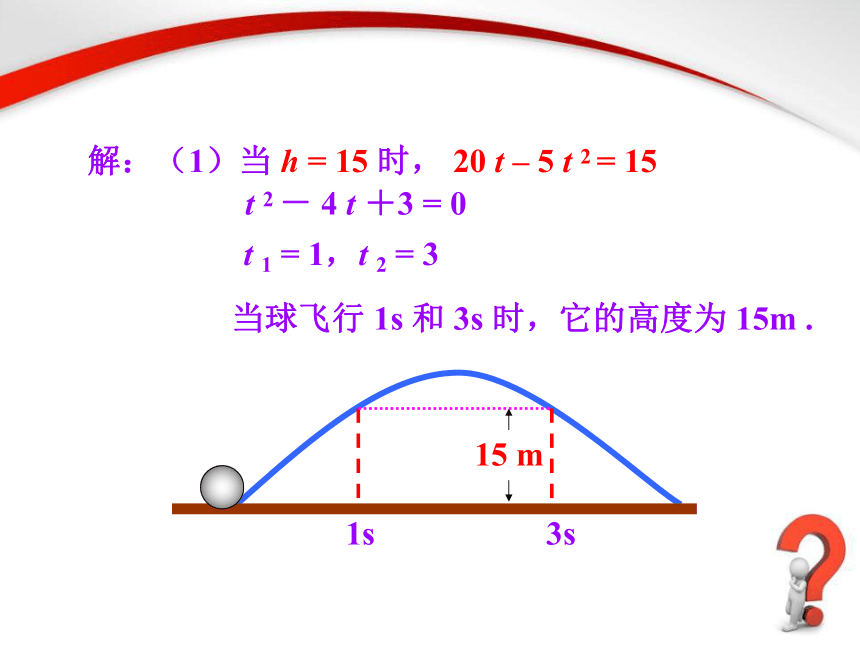
解:(1)当
h
=
15
时,
20
t
–
5
t
2
=
15
t
2
-
4
t
+3
=
0
t
1
=
1,t
2
=
3
当球飞行
1s
和
3s
时,它的高度为
15m
.
1s
3s
15
m
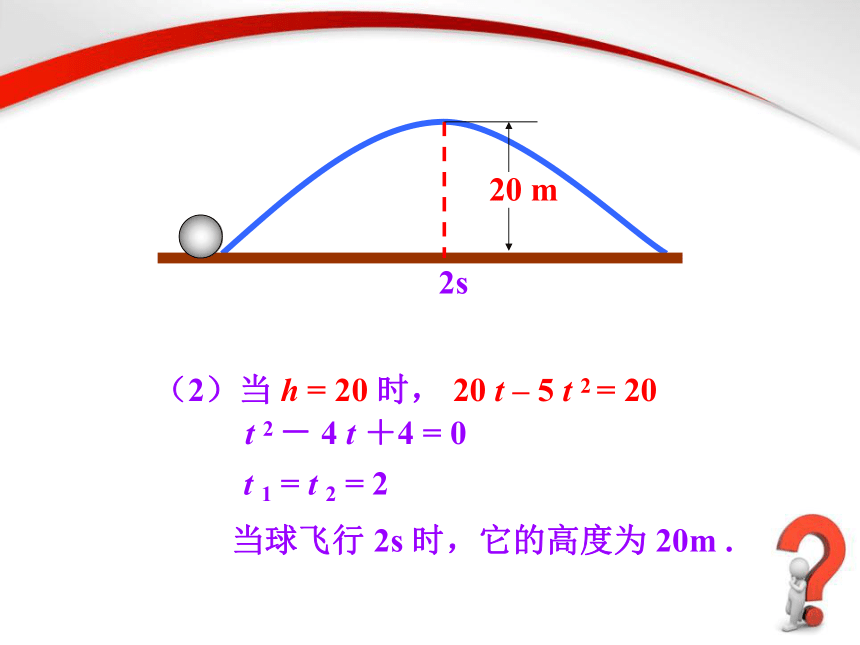
(2)当
h
=
20
时,
20
t
–
5
t
2
=
20
t
2
-
4
t
+4
=
0
t
1
=
t
2
=
2
当球飞行
2s
时,它的高度为
20m
.
2s
20
m
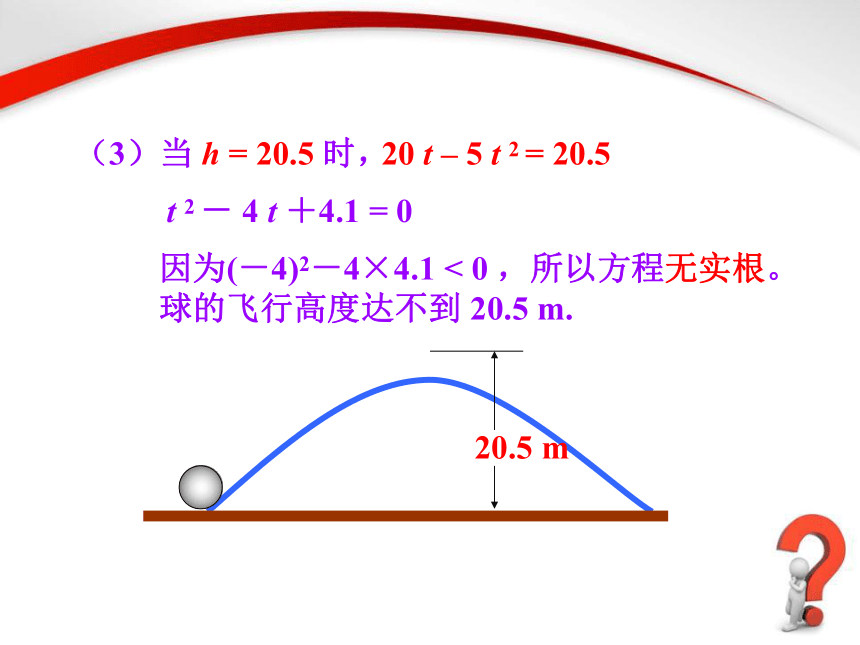
(3)当
h
=
20.5
时,
20
t
–
5
t
2
=
20.5
t
2
-
4
t
+4.1
=
0
因为(-4)2-4×4.1
<
0
,所以方程无实根。
球的飞行高度达不到
20.5
m.
20.5
m
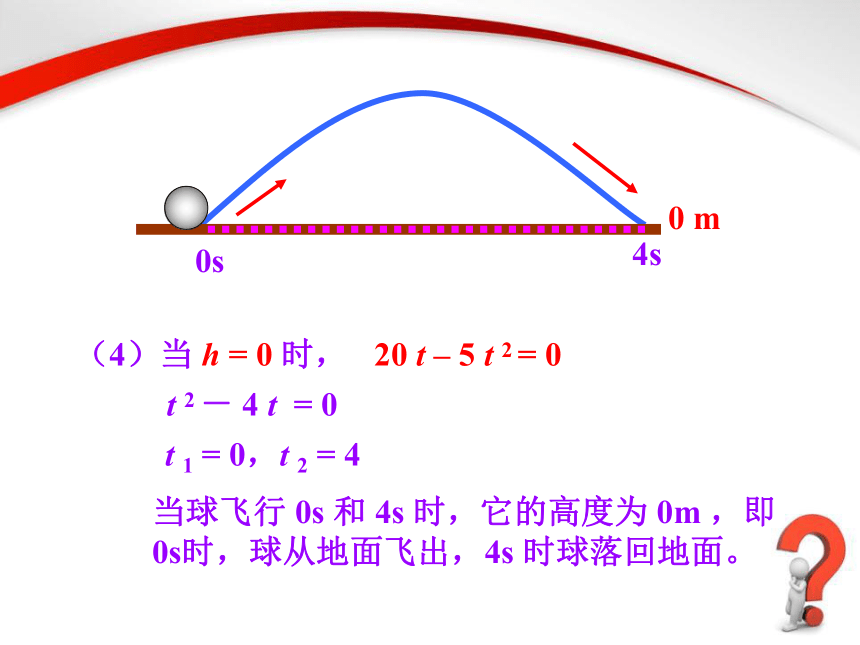
(4)当
h
=
0
时,
20
t
–
5
t
2
=
0
t
2
-
4
t
=
0
t
1
=
0,t
2
=
4
当球飞行
0s
和
4s
时,它的高度为
0m
,即
0s时,球从地面飞出,4s
时球落回地面。
0s
4s
0
m
已知二次函数,求自变量的值
解一元二次方程的根
二次函数与一元二次方程的关系(1)
下列二次函数的图象与
x
轴有交点吗?
若有,求出交点坐标.
(1)
y
=
2x2+x-3
(2)
y
=
4x2
-4x
+1
(3)
y
=
x2
–
x+
1
探究
x
y
o
令
y=
0,解一元二次方程的根
(1)
y
=
2x2+x-3
解:当
y
=
0
时,
2x2+x-3
=
0
(2x+3)(x-1)
=
0
x
1
=
,x
2
=
1
-
3
2
所以与
x
轴有交点,有两个交点。
x
y
o
y
=a(x-x1)(x-
x
1)
二次函数的两点式
(2)
y
=
4x2
-4x
+1
解:当
y
=
0
时,
4x2
-4x
+1
=
0
(2x-1)2
=
0
x
1
=
x
2
=
所以与
x
轴有一个交点。
1
2
x
y
o
(3)
y
=
x2
–
x+
1
解:当
y
=
0
时,
x2
–
x+
1
=
0
所以与
x
轴没有交点。
x
y
o
因为(-1)2-4×1×1
=
-3
<
0
确定二次函数图象与
x
轴的位置关系
解一元二次方程的根
二次函数与一元二次方程的关系(2)
有两个根
有一个根(两个相同的根)
没有根
有两个交点
有一个交点
没有交点
b2
–
4ac
>
0
b2
–
4ac
=
0
b2
–
4ac
<
0
二次函数
y=ax2+bx+c
的图象和x轴交点的三种情况与一元二次方程根的关系
ax2+bx+c
=
0
的根
y=ax2+bx+c
的图象与x轴
若抛物线
y=ax2+bx+c
与
x
轴有交点,则________________
。
b2
–
4ac
≥
0
△>0
△=0
△<0
o
x
y
△
=
b2
–
4ac
课堂小结
二次函数
y=ax2+bx+c
的图象和x轴交点的三种情况与一元二次方程根的关系:
二次函数y=ax2+bx+c的图象和x轴交点
一元二次方程ax2+bx+c=
0的根
一元二次方程ax2+bx+c=
0根的判别式Δ=b2-4ac
有两个交点
有两个不相等的实数根
只有一个交点
有两个相等的实数根
没有交点
没有实数根
b2
–
4ac
>
0
b2
–
4ac
=
0
b2
–
4ac
<
0
随堂练习
1.不与x轴相交的抛物线是(
)
A.
y
=
2x2
–
3
B.
y=-2
x2
+
3
C.
y=
-x2
–
3x
D.
y=-2(x+1)2
-3
2.若抛物线
y
=
ax2+bx+c=
0,当
a>0,c<0时,图象与x轴交点情况是(
)
A.
无交点
B.
只有一个交点
C.
有两个交点
D.
不能确定
D
C
3.
如果关于x的一元二次方程
x2-2x+m=0有两个相等的实数根,则m=___,此时抛物线
y=x2-2x+m与x轴有__个交点.
4.已知抛物线
y=x2
–
8x
+
c的顶点在
x轴上,则
c
=__.
1
1
16
5.若抛物线
y=x2
+
bx+
c
的顶点在第一象限,则方程
x2
+
bx+
c
=0
的根的情况是_____.
b2-4ac
<
0
6.抛物线
y=2x2-3x-5
与y轴交于点____,与x轴交于点 .
7.一元二次方程
3
x2+x-10=0的两个根是x1-2
,x2=5/3,那么二次函数
y=
3
x2+x-10与x轴的交点坐标是________.
(0,-5)
(5/2,0)
(-1,0)
(-2,0)
(5/3,0)
8.已知抛物线y
=
ax2+bx+c的图象如图,则关于x的方程ax2
+
bx
+
c-3
=
0根的情况是(
)
A.
有两个不相等的实数根
B.
有两个异号的实数根
C.
有两个相等的实数根
D.
没有实数根
x
A
o
y
x=-1
3
-1
1.3
.
9.根据下列表格的对应值:
判断方程
ax2+bx+c
=0
(a≠0,a,b,c为常数)一个解x的范围是(
)
A.
3<
x
<
3.23
B.
3.23
<
x
<
3.24
C.
3.24
3.25
D.
3.25
3.26
x
3.23
3.24
3.25
3.26
y=ax2+bx+c
-0.06
-0.02
0.03
0.09
C
10.
已知抛物线
和直线
相交于点P(3,4m)。
(1)求这两个函数的关系式;
(2)当x取何值时,抛物线与直线相交,并求交点坐标。
解:(1)因为点P(3,4m)在直线
上,所以
,解得m=1
所以
,P(3,4)。因为点P(3,4)在抛物线
上,所以有4=18-24+k+8
解得
k=2
所以
(2)依题意,得
解这个方程组,得
所以抛物线与直线的两个交点坐标分别是(3,4),(1.5,2.5)。
习题答案
(1)略.
(2)1,3.
(1)x1
=
1,x2
=
2;(2)x1
=
x2
=
-3
;
(3)没有实数根;
(4)x1
=
-1,x2
=
.
3.
(1)略.
(2)10m.
4.
x
=
1
1
2
3
x
y
O
例:利用函数图象求方程x2-2x-2=0的实数根(精确到0.1)
(-0.7,0)
(2.7,0)
解:作的
图象(右图),它与x轴的公共点的横坐标大约是
.
所以方程
的实数根为
我们还可以通过不断缩小根所在的范围估计一元二次方程的根。
1
2
3
x
y
O
x=2时,y<0
x=3时,y>0
∴根在2到3之间
1
2
3
x
y
O
2.5
已知x=3,y>0
x=2.5时,y<0
∴根在2.5到3之间
1
2
3
x
y
O
1
2
3
x
y
O
2.5
已知x=2.5时,y<0
x=2.75时,y>0
∴根在2.5到2.75之间
2.75
重复上述步骤,我们逐步得到:这个根在2.625,2.75之间,在2.6875,2.75之间……可以得到:
根所在的范围越来越小,根所在的范围的两端的值越来越接近根的值,因而可以作为根的近似值,例如,当要求根的近似值与根的准确值的差的绝对值小于0.1时,由于|2.6875-2.75|=0.0625<0.1,我们可以将2.6875作为根的近似值。
小结
四、布置作业
巩固提高
必做题
P47
2、3、4
选做题
P47
5、6
二次函数与一元二次方程
第二章
二次函数
回顾旧知
二次函数的一般式:
(a≠0)
______是自变量,____是____的函数。
x
y
x
当
y
=
0
时,
ax?
+
bx
+
c
=
0
ax?
+
bx
+
c
=
0
这是什么方程?
九年级上册中我们学习了“一元二次方程”
一元二次方程与二次函数有什么关系?
教学目标
【知识与能力】
总结出二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系,表述何时方程有两个不等的实根、两个相等的实数和没有实根。
会利用二次函数的图象求一元二次方程的近似解。
通过观察二次函数图象与
x
轴的交点个数,讨论一元二次方程的根的情况,进一步体会数形结合思想。
【情感态度与价值观】
【过程与方法】
经历探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系。
教学重难点
二次函数与一元二次方程之间的关系。
利用二次函数图像求一元二次方程的实数根。
一元二次方程根的情况与二次函数图像与x轴位置关系的联系,数形结合思想的运用。
利用二次函数的图象求一元二次方程的近似解。
以
40
m
/s的速度将小球沿与地面成
30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度
h
(单位:m)与飞行时间
t
(单位:s)之间具有关系:h=
20
t
–
5
t
2
考虑下列问题:
(1)球的飞行高度能否达到
15
m?
若能,需要多少时间?
(2)球的飞行高度能否达到
20
m?
若能,需要多少时间?
(3)球的飞行高度能否达到
20.5
m?为什么?
(4)球从飞出到落地要用多少时间?
实际问题
解:(1)当
h
=
15
时,
20
t
–
5
t
2
=
15
t
2
-
4
t
+3
=
0
t
1
=
1,t
2
=
3
当球飞行
1s
和
3s
时,它的高度为
15m
.
1s
3s
15
m
(2)当
h
=
20
时,
20
t
–
5
t
2
=
20
t
2
-
4
t
+4
=
0
t
1
=
t
2
=
2
当球飞行
2s
时,它的高度为
20m
.
2s
20
m
(3)当
h
=
20.5
时,
20
t
–
5
t
2
=
20.5
t
2
-
4
t
+4.1
=
0
因为(-4)2-4×4.1
<
0
,所以方程无实根。
球的飞行高度达不到
20.5
m.
20.5
m
(4)当
h
=
0
时,
20
t
–
5
t
2
=
0
t
2
-
4
t
=
0
t
1
=
0,t
2
=
4
当球飞行
0s
和
4s
时,它的高度为
0m
,即
0s时,球从地面飞出,4s
时球落回地面。
0s
4s
0
m
已知二次函数,求自变量的值
解一元二次方程的根
二次函数与一元二次方程的关系(1)
下列二次函数的图象与
x
轴有交点吗?
若有,求出交点坐标.
(1)
y
=
2x2+x-3
(2)
y
=
4x2
-4x
+1
(3)
y
=
x2
–
x+
1
探究
x
y
o
令
y=
0,解一元二次方程的根
(1)
y
=
2x2+x-3
解:当
y
=
0
时,
2x2+x-3
=
0
(2x+3)(x-1)
=
0
x
1
=
,x
2
=
1
-
3
2
所以与
x
轴有交点,有两个交点。
x
y
o
y
=a(x-x1)(x-
x
1)
二次函数的两点式
(2)
y
=
4x2
-4x
+1
解:当
y
=
0
时,
4x2
-4x
+1
=
0
(2x-1)2
=
0
x
1
=
x
2
=
所以与
x
轴有一个交点。
1
2
x
y
o
(3)
y
=
x2
–
x+
1
解:当
y
=
0
时,
x2
–
x+
1
=
0
所以与
x
轴没有交点。
x
y
o
因为(-1)2-4×1×1
=
-3
<
0
确定二次函数图象与
x
轴的位置关系
解一元二次方程的根
二次函数与一元二次方程的关系(2)
有两个根
有一个根(两个相同的根)
没有根
有两个交点
有一个交点
没有交点
b2
–
4ac
>
0
b2
–
4ac
=
0
b2
–
4ac
<
0
二次函数
y=ax2+bx+c
的图象和x轴交点的三种情况与一元二次方程根的关系
ax2+bx+c
=
0
的根
y=ax2+bx+c
的图象与x轴
若抛物线
y=ax2+bx+c
与
x
轴有交点,则________________
。
b2
–
4ac
≥
0
△>0
△=0
△<0
o
x
y
△
=
b2
–
4ac
课堂小结
二次函数
y=ax2+bx+c
的图象和x轴交点的三种情况与一元二次方程根的关系:
二次函数y=ax2+bx+c的图象和x轴交点
一元二次方程ax2+bx+c=
0的根
一元二次方程ax2+bx+c=
0根的判别式Δ=b2-4ac
有两个交点
有两个不相等的实数根
只有一个交点
有两个相等的实数根
没有交点
没有实数根
b2
–
4ac
>
0
b2
–
4ac
=
0
b2
–
4ac
<
0
随堂练习
1.不与x轴相交的抛物线是(
)
A.
y
=
2x2
–
3
B.
y=-2
x2
+
3
C.
y=
-x2
–
3x
D.
y=-2(x+1)2
-3
2.若抛物线
y
=
ax2+bx+c=
0,当
a>0,c<0时,图象与x轴交点情况是(
)
A.
无交点
B.
只有一个交点
C.
有两个交点
D.
不能确定
D
C
3.
如果关于x的一元二次方程
x2-2x+m=0有两个相等的实数根,则m=___,此时抛物线
y=x2-2x+m与x轴有__个交点.
4.已知抛物线
y=x2
–
8x
+
c的顶点在
x轴上,则
c
=__.
1
1
16
5.若抛物线
y=x2
+
bx+
c
的顶点在第一象限,则方程
x2
+
bx+
c
=0
的根的情况是_____.
b2-4ac
<
0
6.抛物线
y=2x2-3x-5
与y轴交于点____,与x轴交于点 .
7.一元二次方程
3
x2+x-10=0的两个根是x1-2
,x2=5/3,那么二次函数
y=
3
x2+x-10与x轴的交点坐标是________.
(0,-5)
(5/2,0)
(-1,0)
(-2,0)
(5/3,0)
8.已知抛物线y
=
ax2+bx+c的图象如图,则关于x的方程ax2
+
bx
+
c-3
=
0根的情况是(
)
A.
有两个不相等的实数根
B.
有两个异号的实数根
C.
有两个相等的实数根
D.
没有实数根
x
A
o
y
x=-1
3
-1
1.3
.
9.根据下列表格的对应值:
判断方程
ax2+bx+c
=0
(a≠0,a,b,c为常数)一个解x的范围是(
)
A.
3<
x
<
3.23
B.
3.23
<
x
<
3.24
C.
3.24
D.
3.25
x
3.23
3.24
3.25
3.26
y=ax2+bx+c
-0.06
-0.02
0.03
0.09
C
10.
已知抛物线
和直线
相交于点P(3,4m)。
(1)求这两个函数的关系式;
(2)当x取何值时,抛物线与直线相交,并求交点坐标。
解:(1)因为点P(3,4m)在直线
上,所以
,解得m=1
所以
,P(3,4)。因为点P(3,4)在抛物线
上,所以有4=18-24+k+8
解得
k=2
所以
(2)依题意,得
解这个方程组,得
所以抛物线与直线的两个交点坐标分别是(3,4),(1.5,2.5)。
习题答案
(1)略.
(2)1,3.
(1)x1
=
1,x2
=
2;(2)x1
=
x2
=
-3
;
(3)没有实数根;
(4)x1
=
-1,x2
=
.
3.
(1)略.
(2)10m.
4.
x
=
1
1
2
3
x
y
O
例:利用函数图象求方程x2-2x-2=0的实数根(精确到0.1)
(-0.7,0)
(2.7,0)
解:作的
图象(右图),它与x轴的公共点的横坐标大约是
.
所以方程
的实数根为
我们还可以通过不断缩小根所在的范围估计一元二次方程的根。
1
2
3
x
y
O
x=2时,y<0
x=3时,y>0
∴根在2到3之间
1
2
3
x
y
O
2.5
已知x=3,y>0
x=2.5时,y<0
∴根在2.5到3之间
1
2
3
x
y
O
1
2
3
x
y
O
2.5
已知x=2.5时,y<0
x=2.75时,y>0
∴根在2.5到2.75之间
2.75
重复上述步骤,我们逐步得到:这个根在2.625,2.75之间,在2.6875,2.75之间……可以得到:
根所在的范围越来越小,根所在的范围的两端的值越来越接近根的值,因而可以作为根的近似值,例如,当要求根的近似值与根的准确值的差的绝对值小于0.1时,由于|2.6875-2.75|=0.0625<0.1,我们可以将2.6875作为根的近似值。
小结
四、布置作业
巩固提高
必做题
P47
2、3、4
选做题
P47
5、6
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
