北师大版七年级上册数学《3.4整式的加减》课件(20张)
文档属性
| 名称 | 北师大版七年级上册数学《3.4整式的加减》课件(20张) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-16 13:13:06 | ||
图片预览







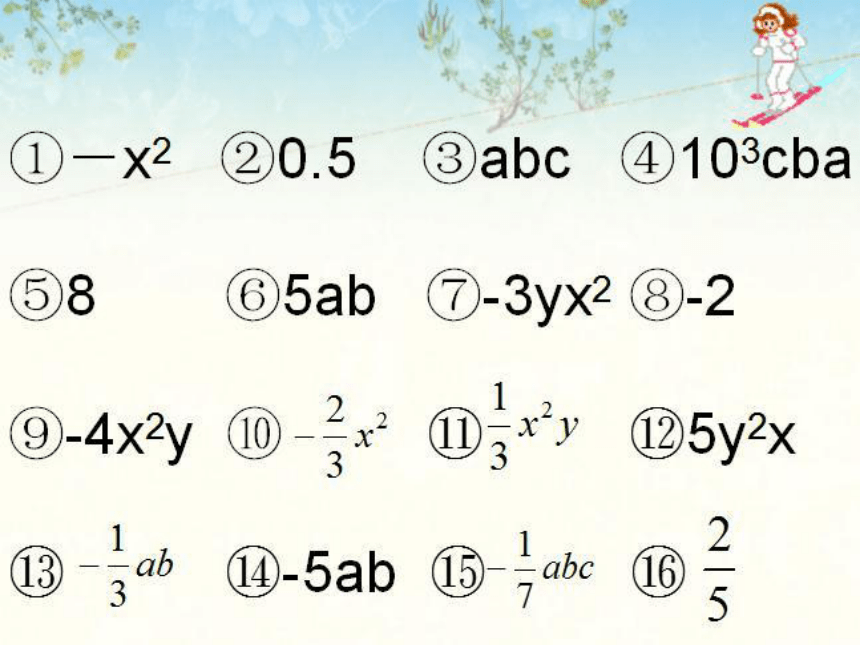
文档简介
(共20张PPT)
第三章
整式及其加减
北师大版数学七年级上册
3.4整式的加减(一)
超市货物摆放
药店药品摆放
垃圾分类
1.准确理解并掌握同类项的概念与特点.
2.在具体情景中理解合并同类项的法则和步骤,能用合并同类项的方法化简多项式,并求代数式的值.
3.初步认识数学与人类生活的密切联系,培养创新意识和探究、观察、概括的能力.
【学习重点】同类项的定义以及合并同类项的法则.
【学习难点】找出同类项并能正确合并同类项.
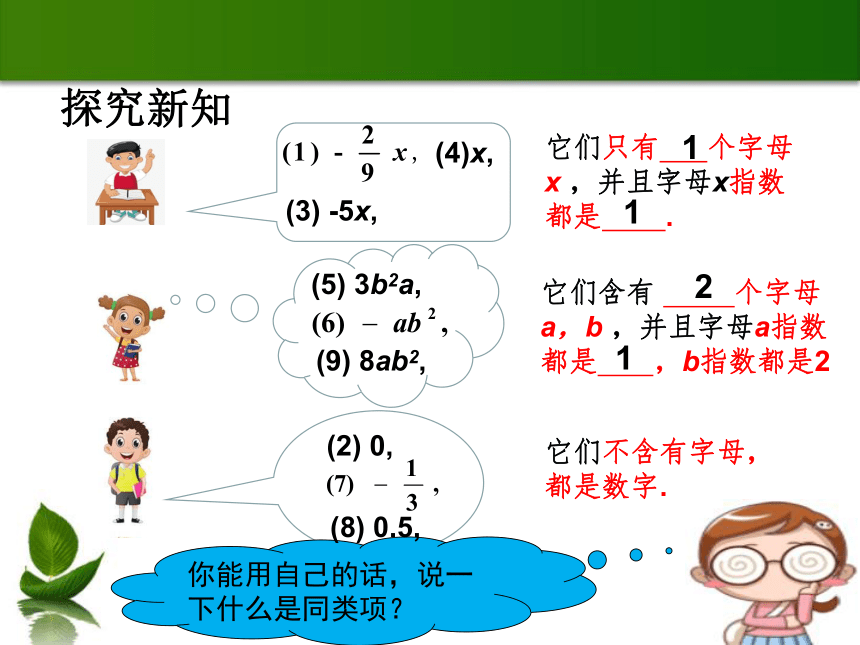
探究新知
(2)
0,
(3)
-5x,
(4)
x,
(5)
3b2a,
(9)
8ab2,
例1:仔细观察下列单项式,认真思考,它们可以如何进行归类?你归类的依据是什么?
知识点
1
同类项
(8)
0.5,
(6)
-ab2,
探究新知
(3)
-5x,
(4)x,
它们只有
个字母x
,并且字母x指数都是
.
(5)
3b2a,
(9)
8ab2,
它们含有
个字母a,b
,并且字母a指数都是
,b指数都是2
(2)
0,
它们不含有字母,
都是数字.
你能用自己的话,说一下什么是同类项?
(8)
0.5,
1
1
2
1
同类项的定义:
所含字母相同,并且相同字母的指数也相同的项叫做同类项.
-2a2b和3ba2
是同类项吗?
2ab和3abc
是同类项吗?
-2a2b和3ab2
是同类项吗?
1.所含的字母相同
2.相同字母的指数也相同
同类项
×
×
3和-4是同类项吗?
教师点拨:
(1)同类项与它们相同字母的顺序无关.
(2)同类项与系数大小无关;
(3)所有的有理数也是同类项;
课本P90熟读记忆定义
规则:
(1)现在老师手里有16张写有单项式的卡片发给同学们;
(2)老师随机叫一名同学站到前面来,并面对全班同学高举自己的卡片;
(3)其他15名同学观察自己手中的卡片,认为和前面的同学是同类项的,也请站到前面来;
(4)请其他同学做裁判,看看有没有找错朋友。
找同类项朋友
若
3x2y3
与
-5xmyn
是同类项,
则m=
,n=
.
若
2x2yn+1
与
-4xmy3
是同类项,
则m=
,n=
.
x
x
x
2
+
3
=
5
=2
6
-
a2bc
a2bc
a2bc
4
奇妙的替换
进一步思考,用到了什么运算律?
知识点
2
合并同类项
仔细观察一下,系数如何变化?字母和字母指数?
课本p90法则(蓝框),熟读记忆
把同类项合并成一项叫做合并同类项.
利用乘法分配律也可得
(2+3)
x
x
2
+
3
=
x
=
6
a2bc
a2bc
a2bc
-4
(6-4)
=
5x
=2a2bc
思考:-3a2b与5b2a能不能合并?
合并同类项的法则是:
把同类项的系数相加,字母和字母的指数不变.
下列各题合并同类项的结果对不对?不对的,指出错在哪里.
(1)a+a=2a
(2)3a+2b=5ab
(3)a-5a=4a
(4)3x2+2x3=5x5
(5)4x2y-5xy2=-x2y
(6)81m-11m=70
×
不是同类项不可以合并
-4a
不是同类项不可以合并
不是同类项不可以合并
字母及字母的次数该写下来
×
×
√
×
×
(2)-4ab+1/3b2-9ab-1/2b2
=(-4ab-9ab)+(1/3b2-1/2b2)
=-13ab-1/6b2
归纳总结:
1.找:准确地找出同类项;
2.移:移动单项式的位置,把同类项放在一起,移动位置时不要丢掉单项式前面的符号;
3.并:把同类项的系数加在一起,字母和字母的指数不变.写出合并后的结果.
解:(1)3a+2b-5a-b
=(3a-5a)+(2b-b)
=(3-5)a+(2-1)b
=-2a+b
例4
求代数式-3x2y+5x-0.5x2y+3.5x2y-2的值,其中x=1/5,y=7.
解:-3x2y+5x-0.5x2y+3.5x2y-2
=(-3x2y-0.5x2y+3.5x2y)+5x-2
=5x-2
当x
=1/5时,y=7时,
原式=5x-2
=5×1/5-2
=-1.
仔细审题,你能想到几种方法?
练习:先化简,再求值6x+2x2-3x+x2+1,其中x=-5.
整式的加减
同类项的特点
课堂小结
1.所含的字母相同
2.相同字母的指数也相同
合并同类项的法则
把同类项的系数相加,字母和字母的指数不变.
合并同类项的步骤
1.找:准确地找出同类项;
2.移:通过交换律把同类项放在一起,交换位置时一定不要丢掉单项式前面的符号;
3.合并:利用合并同类项法则合并同类项,把同类项的系数加在一起,字母和字母的指数不变.
谢谢!
第三章
整式及其加减
北师大版数学七年级上册
3.4整式的加减(一)
超市货物摆放
药店药品摆放
垃圾分类
1.准确理解并掌握同类项的概念与特点.
2.在具体情景中理解合并同类项的法则和步骤,能用合并同类项的方法化简多项式,并求代数式的值.
3.初步认识数学与人类生活的密切联系,培养创新意识和探究、观察、概括的能力.
【学习重点】同类项的定义以及合并同类项的法则.
【学习难点】找出同类项并能正确合并同类项.
探究新知
(2)
0,
(3)
-5x,
(4)
x,
(5)
3b2a,
(9)
8ab2,
例1:仔细观察下列单项式,认真思考,它们可以如何进行归类?你归类的依据是什么?
知识点
1
同类项
(8)
0.5,
(6)
-ab2,
探究新知
(3)
-5x,
(4)x,
它们只有
个字母x
,并且字母x指数都是
.
(5)
3b2a,
(9)
8ab2,
它们含有
个字母a,b
,并且字母a指数都是
,b指数都是2
(2)
0,
它们不含有字母,
都是数字.
你能用自己的话,说一下什么是同类项?
(8)
0.5,
1
1
2
1
同类项的定义:
所含字母相同,并且相同字母的指数也相同的项叫做同类项.
-2a2b和3ba2
是同类项吗?
2ab和3abc
是同类项吗?
-2a2b和3ab2
是同类项吗?
1.所含的字母相同
2.相同字母的指数也相同
同类项
×
×
3和-4是同类项吗?
教师点拨:
(1)同类项与它们相同字母的顺序无关.
(2)同类项与系数大小无关;
(3)所有的有理数也是同类项;
课本P90熟读记忆定义
规则:
(1)现在老师手里有16张写有单项式的卡片发给同学们;
(2)老师随机叫一名同学站到前面来,并面对全班同学高举自己的卡片;
(3)其他15名同学观察自己手中的卡片,认为和前面的同学是同类项的,也请站到前面来;
(4)请其他同学做裁判,看看有没有找错朋友。
找同类项朋友
若
3x2y3
与
-5xmyn
是同类项,
则m=
,n=
.
若
2x2yn+1
与
-4xmy3
是同类项,
则m=
,n=
.
x
x
x
2
+
3
=
5
=2
6
-
a2bc
a2bc
a2bc
4
奇妙的替换
进一步思考,用到了什么运算律?
知识点
2
合并同类项
仔细观察一下,系数如何变化?字母和字母指数?
课本p90法则(蓝框),熟读记忆
把同类项合并成一项叫做合并同类项.
利用乘法分配律也可得
(2+3)
x
x
2
+
3
=
x
=
6
a2bc
a2bc
a2bc
-4
(6-4)
=
5x
=2a2bc
思考:-3a2b与5b2a能不能合并?
合并同类项的法则是:
把同类项的系数相加,字母和字母的指数不变.
下列各题合并同类项的结果对不对?不对的,指出错在哪里.
(1)a+a=2a
(2)3a+2b=5ab
(3)a-5a=4a
(4)3x2+2x3=5x5
(5)4x2y-5xy2=-x2y
(6)81m-11m=70
×
不是同类项不可以合并
-4a
不是同类项不可以合并
不是同类项不可以合并
字母及字母的次数该写下来
×
×
√
×
×
(2)-4ab+1/3b2-9ab-1/2b2
=(-4ab-9ab)+(1/3b2-1/2b2)
=-13ab-1/6b2
归纳总结:
1.找:准确地找出同类项;
2.移:移动单项式的位置,把同类项放在一起,移动位置时不要丢掉单项式前面的符号;
3.并:把同类项的系数加在一起,字母和字母的指数不变.写出合并后的结果.
解:(1)3a+2b-5a-b
=(3a-5a)+(2b-b)
=(3-5)a+(2-1)b
=-2a+b
例4
求代数式-3x2y+5x-0.5x2y+3.5x2y-2的值,其中x=1/5,y=7.
解:-3x2y+5x-0.5x2y+3.5x2y-2
=(-3x2y-0.5x2y+3.5x2y)+5x-2
=5x-2
当x
=1/5时,y=7时,
原式=5x-2
=5×1/5-2
=-1.
仔细审题,你能想到几种方法?
练习:先化简,再求值6x+2x2-3x+x2+1,其中x=-5.
整式的加减
同类项的特点
课堂小结
1.所含的字母相同
2.相同字母的指数也相同
合并同类项的法则
把同类项的系数相加,字母和字母的指数不变.
合并同类项的步骤
1.找:准确地找出同类项;
2.移:通过交换律把同类项放在一起,交换位置时一定不要丢掉单项式前面的符号;
3.合并:利用合并同类项法则合并同类项,把同类项的系数加在一起,字母和字母的指数不变.
谢谢!
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
