北师大版九年级数学上册2.4用因式分解法求解一元二次方程课件(共29张PPT)
文档属性
| 名称 | 北师大版九年级数学上册2.4用因式分解法求解一元二次方程课件(共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-16 21:07:10 | ||
图片预览


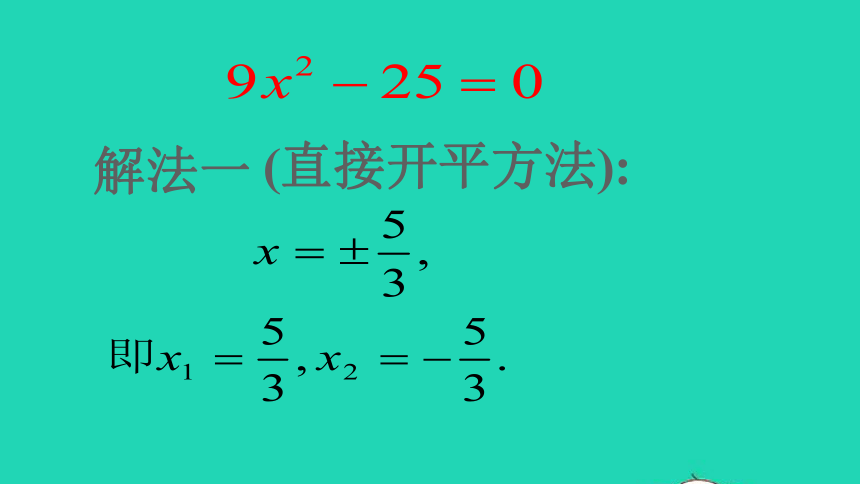



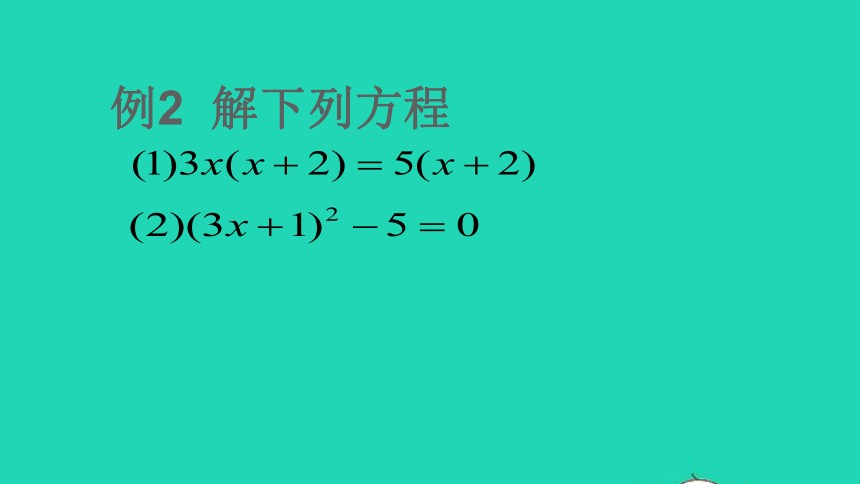


文档简介
4 用因式分解法求解一元二次方程
1.已学过的一元二次方程解法有什么?
直接开平方法
3.请解方程
2.用直接开平方法来解的方程有什么特征?
新课导入
解法一
(直接开平方法):
9x2-25=0
解:原方程可变形为
(3x+5)(3x-5)=0
3x+5=0 或 3x-5=0
9x2-25= (3x+5)(3x-5)
教学目标
1.熟练掌握用因式分解法解一元二次方程.
2.通过因式分解法解一元二次方程的学习,树立转化的思想.
重点 难点
重点:用因式分解法解一元二次方程.
难点:正确理解AB=0?A=0或B=0( A、B表示两个因式).
推进新课
例2 解下列方程
x+2=0或3x-5=0
∴ x1=-2 , x2=
(2)(3x+1)2-5=0
解:原方程可变形为
(3x+1+
)(3x+1-
)=0
3x+1+
=0或3x+1-
=0
∴ x1=
, x2=
用因式分解法解一元二次方程的步骤
1. 方程右边不为零的化为 .
2. 将方程左边分解成两个 的乘积.
3. 至少 一次因式为零,得到两个一元一次方程.
4. 两个 就是原方程的解.
零
一次因式
有一个
一元一次方程的解
例 (x+3)(x-1)=5
解:原方程可变形为
(x-2)(x+4)=0
x-2=0或x+4=0
∴ x1=2 ,x2=-4
解题步骤演示
x2+2x-8 =0
方程右边化为零
左边分解成两个一次因式 的乘积
至少有一个一次因式为零得到两个一元一次方程
两个一元一次方程的解就是原方程的解
快速回答:下列各方程的根分别是多少?
AB=0?A=0或B=0
这样解是否正确呢?
方程的两边同时除以同一个不等于零的数,所得的方程与原方程 同解.
注:如果一元二次方程有实数根,那么一定有两个实数根.
下面的解法正确吗?如果不正确,错误在哪?
( )
当一元二次方程的一边为0 ,而另一边易于分解成两个一次因式时,就可以用因式分解法来解.
0
用因式分解法解下列方程:
y2=3y
(2) (2a-3)2=(a-2)(3a-4)
(3)
(4) x2+7x+12=0
(1) (x-5)(x+2)=18
x2-3x-28=0
(x-7)(x+4)=0
x-7=0,或x+4=0
x1=7,x2= -4
右化零 左分解
两因式 各求解
简记歌诀:
因式分解法解题框架图
解:原方程可变形为:
=0
( )( )=0
=0或 =0
∴ x1= , x2=
一次因式A
一次因式A
一次因式B
一次因式B
B解
A解
(1) (4x-3)2=(x+3)2
解方程:(拓展)练习:
随堂演练
通过这节课的学习,你有什么收获?
课堂小结
1.已学过的一元二次方程解法有什么?
直接开平方法
3.请解方程
2.用直接开平方法来解的方程有什么特征?
新课导入
解法一
(直接开平方法):
9x2-25=0
解:原方程可变形为
(3x+5)(3x-5)=0
3x+5=0 或 3x-5=0
9x2-25= (3x+5)(3x-5)
教学目标
1.熟练掌握用因式分解法解一元二次方程.
2.通过因式分解法解一元二次方程的学习,树立转化的思想.
重点 难点
重点:用因式分解法解一元二次方程.
难点:正确理解AB=0?A=0或B=0( A、B表示两个因式).
推进新课
例2 解下列方程
x+2=0或3x-5=0
∴ x1=-2 , x2=
(2)(3x+1)2-5=0
解:原方程可变形为
(3x+1+
)(3x+1-
)=0
3x+1+
=0或3x+1-
=0
∴ x1=
, x2=
用因式分解法解一元二次方程的步骤
1. 方程右边不为零的化为 .
2. 将方程左边分解成两个 的乘积.
3. 至少 一次因式为零,得到两个一元一次方程.
4. 两个 就是原方程的解.
零
一次因式
有一个
一元一次方程的解
例 (x+3)(x-1)=5
解:原方程可变形为
(x-2)(x+4)=0
x-2=0或x+4=0
∴ x1=2 ,x2=-4
解题步骤演示
x2+2x-8 =0
方程右边化为零
左边分解成两个一次因式 的乘积
至少有一个一次因式为零得到两个一元一次方程
两个一元一次方程的解就是原方程的解
快速回答:下列各方程的根分别是多少?
AB=0?A=0或B=0
这样解是否正确呢?
方程的两边同时除以同一个不等于零的数,所得的方程与原方程 同解.
注:如果一元二次方程有实数根,那么一定有两个实数根.
下面的解法正确吗?如果不正确,错误在哪?
( )
当一元二次方程的一边为0 ,而另一边易于分解成两个一次因式时,就可以用因式分解法来解.
0
用因式分解法解下列方程:
y2=3y
(2) (2a-3)2=(a-2)(3a-4)
(3)
(4) x2+7x+12=0
(1) (x-5)(x+2)=18
x2-3x-28=0
(x-7)(x+4)=0
x-7=0,或x+4=0
x1=7,x2= -4
右化零 左分解
两因式 各求解
简记歌诀:
因式分解法解题框架图
解:原方程可变形为:
=0
( )( )=0
=0或 =0
∴ x1= , x2=
一次因式A
一次因式A
一次因式B
一次因式B
B解
A解
(1) (4x-3)2=(x+3)2
解方程:(拓展)练习:
随堂演练
通过这节课的学习,你有什么收获?
课堂小结
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
