人教版 七年级数学上册 2.1 整式 针对训练 (Word版 含答案)
文档属性
| 名称 | 人教版 七年级数学上册 2.1 整式 针对训练 (Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 202.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-15 20:07:56 | ||
图片预览


文档简介
人教版
七年级数学
2.1
整式
针对训练
一、选择题
1.
我们知道,用字母表示的式子具有一般意义,则下列赋予3a实际意义的例子中不正确的是( )
A.若葡萄的单价是3元/千克,则3a元表示购买a千克该种葡萄的金额
B.若a表示一个等边三角形的边长,则3a表示这个等边三角形的周长
C.王师傅每天做a个零件,则3a个表示王师傅3天做的零件个数
D.若3和a分别表示一个两位数的十位数字和个位数字,则3a表示这个两位数
2.
某商品打七折后价格为a元,则该商品的原价为( )
A.a元
B.a元
C.30%a元
D.a元
3.
用式子表示“x的2倍与y的和的平方”是
( )
A.(2x+y)2
B.2x+y2
C.2x2+y2
D.x(2+y)2
4.
多项式2x2-x-3的项分别是( )
A.2x2,x,3
B.2x2,-x,-3
C.2x2,x,-3
D.2x2,-x,3
5.
下列说法正确的是( )
A.-1不是单项式
B.2πr2的次数是3
C.的次数是3
D.-的系数是-1
6.
关于单项式-xy3z2,下列说法正确的是
( )
A.系数是1,次数是5
B.系数是-1,次数是6
C.系数是1,次数是6
D.系数是-1,次数是5
7.
正方体的棱长为a,那么它的表面积和体积分别是( )
A.6a,a3
B.6a2,a3
C.6a3,a3
D.6a,3a3
8.
在一列数:a1,a2,a3,…an中,a1=7,a2=1,从第三个数开始,每一个数都等于它前面两个数之积的个位数字,则这个数中的第2020个数是( )
A.1
B.3
C.7
D.9
9.
观察下面的一列单项式:-x,2x2,-4x3,8x4,-16x5,…,根据其中的规律,得出第10个单项式是( )
A.-29x10
B.29x10
C.-29x9
D.29x9
10.
如图,在2020年10月份的月历表上,任意圈出一个正方形,则下列等式中错误的是( )
A.a+d=b+c
B.a-c=b-d
C.a-b=c-d
D.d-a=c-b
二、填空题
11.
体育委员小金带了500元钱去买体育用品,已知一个足球x元,一个篮球y元,则式子500-3x-2y表示的实际意义是___________________.
12.
妞妞家新装修了楼房,每面墙上都贴有长方形的壁纸,每张壁纸长a
m,宽b
m.如果所用壁纸的张数为n,那么墙壁的面积S为________m2,这个式子是________项式,系数为________,次数为________(壁纸无重叠、无缝隙).
13.
如图是一个运算程序的示意图,若开始输入的x值为625,则第2018次输出的结果为________.
14.
观察如图所示的“蜂窝图”:
则第n(n是正整数)个图案中“”的个数是________.(用含n的式子表示)
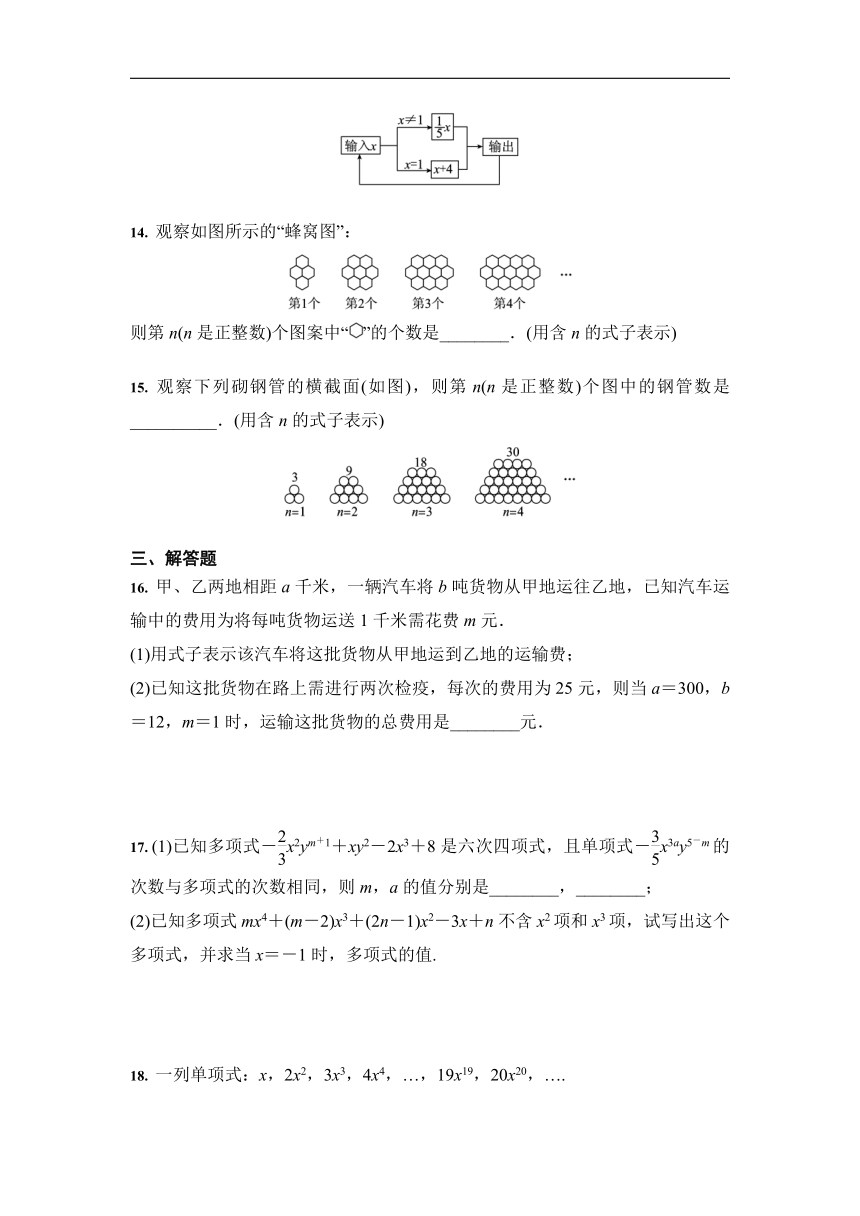
15.
观察下列砌钢管的横截面(如图),则第n(n是正整数)个图中的钢管数是__________.(用含n的式子表示)
三、解答题
16.
甲、乙两地相距a千米,一辆汽车将b吨货物从甲地运往乙地,已知汽车运输中的费用为将每吨货物运送1千米需花费m元.
(1)用式子表示该汽车将这批货物从甲地运到乙地的运输费;
(2)已知这批货物在路上需进行两次检疫,每次的费用为25元,则当a=300,b=12,m=1时,运输这批货物的总费用是________元.
17.
(1)已知多项式-x2ym+1+xy2-2x3+8是六次四项式,且单项式-x3ay5-m的次数与多项式的次数相同,则m,a的值分别是________,________;
(2)已知多项式mx4+(m-2)x3+(2n-1)x2-3x+n不含x2项和x3项,试写出这个多项式,并求当x=-1时,多项式的值.
18.
一列单项式:x,2x2,3x3,4x4,…,19x19,20x20,….
(1)这列单项式有什么规律?
(2)写出第99个,第2020个单项式;
(3)写出第n个,第(n+1)个单项式.
19.
已知关于x,y的多项式x4+(m+2)xny-xy2+3,其中n为正整数.
(1)当m,n为何值时,它是五次四项式?
(2)当m,n为何值时,它是四次三项式?
20.
观察下列一串单项式的特点:xy,-2x2y,4x3y,-8x4y,16x5y,….
(1)按此规律写出第9个单项式;
(2)第n(n为正整数)个单项式为多少?它的系数和次数分别是多少?
人教版
七年级数学
2.1
整式
针对训练
-答案
一、选择题
1.
【答案】D
2.
【答案】B [解析]
该商品的原价为a÷0.7=a(元).故选B.
3.
【答案】A [解析]
先求x的2倍为2x,再求x的2倍与y的和为2x+y,最后求x的2倍与y的和的平方为(2x+y)2.
4.
【答案】B
5.
【答案】C
6.
【答案】B [解析]
-xy3z2是单项式,数字因数为-1,所有字母指数之和为6,所以-xy3z2的系数是-1,次数是6.
7.
【答案】B
8.
【答案】C [解析]
依题意得:a1=7,a2=1,a3=7,a4=7,a5=9,a6=3,a7=7,a8=1,…,
周期为6,2020÷6=336……4,
所以a2020=a4=7.
故选C.
9.
【答案】B
10.
【答案】D
二、填空题
11.
【答案】体育委员小金买了3个足球、2个篮球后剩余的钱数 [解析]
因为3x与2y分别表示买3个足球、2个篮球的费用,所以式子500-3x-2y表示的实际意义是体育委员小金买了3个足球、2个篮球后剩余的钱数.
12.
【答案】nab 单 1 3
13.
【答案】1 [解析]
当x=625时,x=125,
当x=125时,x=25,
当x=25时,x=5,
当x=5时,x=1,
当x=1时,x+4=5,
当x=5时,x=1,
…
(2018-3)÷2=1007……1,
故第2018次输出的结果与第4次输出的结果相同,即输出的结果是1.故答案为1.
14.
【答案】3n+1 [解析]
根据题意可知,第1个图案中有4个“”,第2个图案中有7个“”,第3个图案中有10个“”,第4个图案中有13个“”,由此可得出后一个图案都比前一个图案多3个“”,所以第n个图案中“”的个数为4+3(n-1)=3n+1.故答案为3n+1.
15.
【答案】n(n+1) [解析]
第1个图中钢管数为1+2=3,
第2个图中钢管数为2+3+4=×(2+4)×3=9,
第3个图中钢管数为3+4+5+6=×(3+6)×4=18,
第4个图中钢管数为4+5+6+7+8=×(4+8)×5=30,
…
依此类推,第n个图中钢管数为n+(n+1)+(n+2)+(n+3)+(n+4)+2n=(n+2n)(n+1)=n(n+1).
三、解答题
16.
【答案】
解:(1)abm元.
(2)abm+50=300×12×1+50=3650(元).
即运输这批货物的总费用是3650元.
故答案为3650.
17.
【答案】
[解析]
(1)利用多项式的次数与单项式次数的定义求出m与a的值即可;
(2)由多项式不含x2项和x3项求出m与n的值,再将x=-1代入求值即可.
解:(1)由题意得2+m+1=6,3a+5-m=6,解得m=3,a=.故答案为3,.
(2)因为多项式mx4+(m-2)x3+(2n-1)x2-3x+n不含x2项和x3项,
所以m-2=0,2n-1=0,
解得m=2,n=,
即这个多项式为2x4-3x+.
当x=-1时,原式=2+3+=5.
18.
【答案】
[解析]
通过观察可得:x的系数和次数相等,即是这个数所在的个数,由此可解出本题.
解:(1)第几个单项式,它的系数就是几,x的指数就是几.
(2)第99个单项式是99x99,第2020个单项式是2020x2020.
(3)第n个单项式是nxn,第(n+1)个单项式是(n+1)xn+1.
19.
【答案】
解:(1)因为多项式是五次四项式,
所以m+2≠0,n+1=5.
所以m≠-2,n=4.
(2)因为多项式是四次三项式,
所以m+2=0,n为任意正整数.
所以m=-2,n为任意正整数.
20.
【答案】
解:(1)因为当n=1时,单项式为xy,
当n=2时,单项式为-2x2y,
当n=3时,单项式为4x3y,
当n=4时,单项式为-8x4y,
当n=5时,单项式为16x5y,
所以第9个单项式是29-1x9y,即256x9y.
(2)第n(n为正整数)个单项式为
(-1)n+12n-1xny,
它的系数是(-1)n+12n-1,次数是n+1.
七年级数学
2.1
整式
针对训练
一、选择题
1.
我们知道,用字母表示的式子具有一般意义,则下列赋予3a实际意义的例子中不正确的是( )
A.若葡萄的单价是3元/千克,则3a元表示购买a千克该种葡萄的金额
B.若a表示一个等边三角形的边长,则3a表示这个等边三角形的周长
C.王师傅每天做a个零件,则3a个表示王师傅3天做的零件个数
D.若3和a分别表示一个两位数的十位数字和个位数字,则3a表示这个两位数
2.
某商品打七折后价格为a元,则该商品的原价为( )
A.a元
B.a元
C.30%a元
D.a元
3.
用式子表示“x的2倍与y的和的平方”是
( )
A.(2x+y)2
B.2x+y2
C.2x2+y2
D.x(2+y)2
4.
多项式2x2-x-3的项分别是( )
A.2x2,x,3
B.2x2,-x,-3
C.2x2,x,-3
D.2x2,-x,3
5.
下列说法正确的是( )
A.-1不是单项式
B.2πr2的次数是3
C.的次数是3
D.-的系数是-1
6.
关于单项式-xy3z2,下列说法正确的是
( )
A.系数是1,次数是5
B.系数是-1,次数是6
C.系数是1,次数是6
D.系数是-1,次数是5
7.
正方体的棱长为a,那么它的表面积和体积分别是( )
A.6a,a3
B.6a2,a3
C.6a3,a3
D.6a,3a3
8.
在一列数:a1,a2,a3,…an中,a1=7,a2=1,从第三个数开始,每一个数都等于它前面两个数之积的个位数字,则这个数中的第2020个数是( )
A.1
B.3
C.7
D.9
9.
观察下面的一列单项式:-x,2x2,-4x3,8x4,-16x5,…,根据其中的规律,得出第10个单项式是( )
A.-29x10
B.29x10
C.-29x9
D.29x9
10.
如图,在2020年10月份的月历表上,任意圈出一个正方形,则下列等式中错误的是( )
A.a+d=b+c
B.a-c=b-d
C.a-b=c-d
D.d-a=c-b
二、填空题
11.
体育委员小金带了500元钱去买体育用品,已知一个足球x元,一个篮球y元,则式子500-3x-2y表示的实际意义是___________________.
12.
妞妞家新装修了楼房,每面墙上都贴有长方形的壁纸,每张壁纸长a
m,宽b
m.如果所用壁纸的张数为n,那么墙壁的面积S为________m2,这个式子是________项式,系数为________,次数为________(壁纸无重叠、无缝隙).
13.
如图是一个运算程序的示意图,若开始输入的x值为625,则第2018次输出的结果为________.
14.
观察如图所示的“蜂窝图”:
则第n(n是正整数)个图案中“”的个数是________.(用含n的式子表示)
15.
观察下列砌钢管的横截面(如图),则第n(n是正整数)个图中的钢管数是__________.(用含n的式子表示)
三、解答题
16.
甲、乙两地相距a千米,一辆汽车将b吨货物从甲地运往乙地,已知汽车运输中的费用为将每吨货物运送1千米需花费m元.
(1)用式子表示该汽车将这批货物从甲地运到乙地的运输费;
(2)已知这批货物在路上需进行两次检疫,每次的费用为25元,则当a=300,b=12,m=1时,运输这批货物的总费用是________元.
17.
(1)已知多项式-x2ym+1+xy2-2x3+8是六次四项式,且单项式-x3ay5-m的次数与多项式的次数相同,则m,a的值分别是________,________;
(2)已知多项式mx4+(m-2)x3+(2n-1)x2-3x+n不含x2项和x3项,试写出这个多项式,并求当x=-1时,多项式的值.
18.
一列单项式:x,2x2,3x3,4x4,…,19x19,20x20,….
(1)这列单项式有什么规律?
(2)写出第99个,第2020个单项式;
(3)写出第n个,第(n+1)个单项式.
19.
已知关于x,y的多项式x4+(m+2)xny-xy2+3,其中n为正整数.
(1)当m,n为何值时,它是五次四项式?
(2)当m,n为何值时,它是四次三项式?
20.
观察下列一串单项式的特点:xy,-2x2y,4x3y,-8x4y,16x5y,….
(1)按此规律写出第9个单项式;
(2)第n(n为正整数)个单项式为多少?它的系数和次数分别是多少?
人教版
七年级数学
2.1
整式
针对训练
-答案
一、选择题
1.
【答案】D
2.
【答案】B [解析]
该商品的原价为a÷0.7=a(元).故选B.
3.
【答案】A [解析]
先求x的2倍为2x,再求x的2倍与y的和为2x+y,最后求x的2倍与y的和的平方为(2x+y)2.
4.
【答案】B
5.
【答案】C
6.
【答案】B [解析]
-xy3z2是单项式,数字因数为-1,所有字母指数之和为6,所以-xy3z2的系数是-1,次数是6.
7.
【答案】B
8.
【答案】C [解析]
依题意得:a1=7,a2=1,a3=7,a4=7,a5=9,a6=3,a7=7,a8=1,…,
周期为6,2020÷6=336……4,
所以a2020=a4=7.
故选C.
9.
【答案】B
10.
【答案】D
二、填空题
11.
【答案】体育委员小金买了3个足球、2个篮球后剩余的钱数 [解析]
因为3x与2y分别表示买3个足球、2个篮球的费用,所以式子500-3x-2y表示的实际意义是体育委员小金买了3个足球、2个篮球后剩余的钱数.
12.
【答案】nab 单 1 3
13.
【答案】1 [解析]
当x=625时,x=125,
当x=125时,x=25,
当x=25时,x=5,
当x=5时,x=1,
当x=1时,x+4=5,
当x=5时,x=1,
…
(2018-3)÷2=1007……1,
故第2018次输出的结果与第4次输出的结果相同,即输出的结果是1.故答案为1.
14.
【答案】3n+1 [解析]
根据题意可知,第1个图案中有4个“”,第2个图案中有7个“”,第3个图案中有10个“”,第4个图案中有13个“”,由此可得出后一个图案都比前一个图案多3个“”,所以第n个图案中“”的个数为4+3(n-1)=3n+1.故答案为3n+1.
15.
【答案】n(n+1) [解析]
第1个图中钢管数为1+2=3,
第2个图中钢管数为2+3+4=×(2+4)×3=9,
第3个图中钢管数为3+4+5+6=×(3+6)×4=18,
第4个图中钢管数为4+5+6+7+8=×(4+8)×5=30,
…
依此类推,第n个图中钢管数为n+(n+1)+(n+2)+(n+3)+(n+4)+2n=(n+2n)(n+1)=n(n+1).
三、解答题
16.
【答案】
解:(1)abm元.
(2)abm+50=300×12×1+50=3650(元).
即运输这批货物的总费用是3650元.
故答案为3650.
17.
【答案】
[解析]
(1)利用多项式的次数与单项式次数的定义求出m与a的值即可;
(2)由多项式不含x2项和x3项求出m与n的值,再将x=-1代入求值即可.
解:(1)由题意得2+m+1=6,3a+5-m=6,解得m=3,a=.故答案为3,.
(2)因为多项式mx4+(m-2)x3+(2n-1)x2-3x+n不含x2项和x3项,
所以m-2=0,2n-1=0,
解得m=2,n=,
即这个多项式为2x4-3x+.
当x=-1时,原式=2+3+=5.
18.
【答案】
[解析]
通过观察可得:x的系数和次数相等,即是这个数所在的个数,由此可解出本题.
解:(1)第几个单项式,它的系数就是几,x的指数就是几.
(2)第99个单项式是99x99,第2020个单项式是2020x2020.
(3)第n个单项式是nxn,第(n+1)个单项式是(n+1)xn+1.
19.
【答案】
解:(1)因为多项式是五次四项式,
所以m+2≠0,n+1=5.
所以m≠-2,n=4.
(2)因为多项式是四次三项式,
所以m+2=0,n为任意正整数.
所以m=-2,n为任意正整数.
20.
【答案】
解:(1)因为当n=1时,单项式为xy,
当n=2时,单项式为-2x2y,
当n=3时,单项式为4x3y,
当n=4时,单项式为-8x4y,
当n=5时,单项式为16x5y,
所以第9个单项式是29-1x9y,即256x9y.
(2)第n(n为正整数)个单项式为
(-1)n+12n-1xny,
它的系数是(-1)n+12n-1,次数是n+1.
