冀教版初中数学九上 27.2 反比例函数的图象和性质 教案
文档属性
| 名称 | 冀教版初中数学九上 27.2 反比例函数的图象和性质 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 229.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-01 00:00:00 | ||
图片预览


文档简介
《反比例函数的图像和性质(第2课时)》教学设计
一.教材分析:
1.教材所处的地位和作用:
本节课是在前面学习了建立反比例函数模型,确定反比例函数的表达式以及经历画反比例函数图像的过程的基础上,把反比例函数的表达式及图像有机地结合在一起,探索并理解反比例函数的性质,是对前面两节内容的归纳和概括,既体现了数形结合的思想,又发展了学生分析、归纳的能力。
2.教学目标:
(1)、知识与技能:通过反比例函数的表达式及图像的确立,经历探索反比例函数性质的过程,理解并掌握反比例函数的性质。
(2)、过程与方法:通过探索反比例函数性质的过程,培养观察、分析、归纳和概括的能力,提高从图像中获取信息的能力。
(3)、情感态度与价值观:通过感受反比例函数图像变化的乐趣,培养学生学习的毅力和信心。
3.教学重点:
本节课的教学重点为:归纳概括出图像位置及y随x的变化规律与常数k的关系,发展学生数形结合的思想。
4.教学难点:
对反比例函数性质全面、深入的理解以及应用性质解决实际问题,注重函数观念的形成,培养数学应用能力。
二.教法、学法:
1.教法分析:
本课是一节典型的通过观察反比例函数图像来归纳反比例函数性质的探究课,为突出重点,有效的突破难点,结合本节课的内容,我在教法设计上:以观察、探究、归纳法为主,辅以启发式教学和情感教学;教学手段上:以多媒体为教学平台,用形象的动画和生动的语言激发学生的学习兴趣,不断创设情境,层层深入,互动交流,使学生积极主动地参与到活动中来,成为学习的主体。
2.学法指导:
本节课在充分发挥学生主体地位的基础上进行学法指导,关注学生观察、探究过程,关注学生归纳,总结的规律,在交流中获得自己对数学知识的方法和能力,增强学生数学学习的信心。
三.教学程序:
(一)旧知回顾,提出问题:
我们已经学习了正比例函数的图像和性质,同学们还记得吗?
设计意图:由于本节课内容的特点,要想学好本节课,必须要正确处理好知识的衔接,所以,我在这个环节设置了正比例函数图像性质的复习知识,并以形象的数形结合的形式展现在学生的眼前,把枯燥的数学知识增加了无限的趣味,抓住了学生的注意力,激发学生的探究欲望。
通常学习一种函数,都要由他们的图像得出性质,那么反比例函数的图像会有什么性质呢?
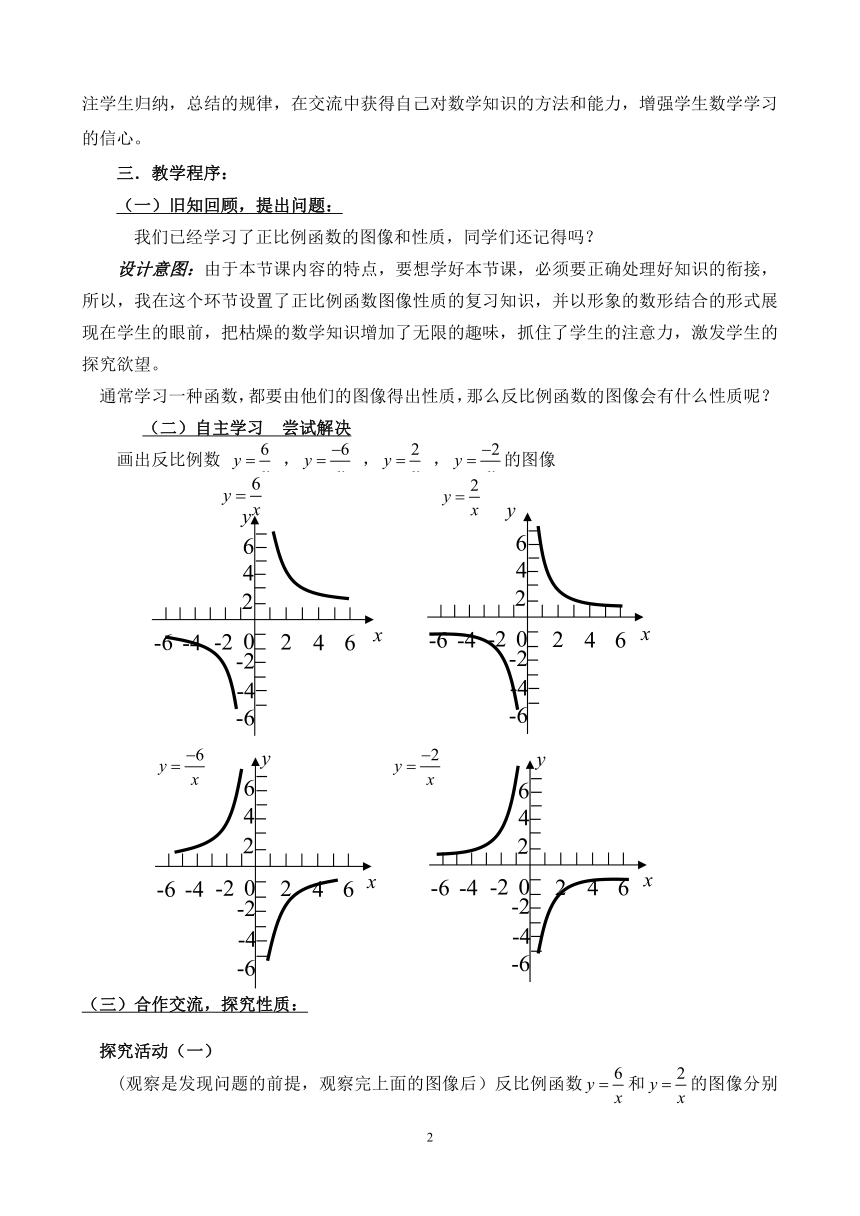
(二)自主学习
尝试解决
画出反比例数
,
,
,的图像
(三)合作交流,探究性质:
探究活动(一)
(观察是发现问题的前提,观察完上面的图像后)反比例函数和的图像分别位于哪两个象限内?反比例函数和的图像分别位于哪两个象限内?反比例函数的图像所在象限和
k
是正数还是负数有什么关系?
活动过程:
(1)学生结合函数图象归纳总结:反比例函数的图像当k
>0时,图像的两个分支分别位于第一、三象限内;当k
<
0时,图像的两个分支分别位于第二、四象限内这一事实,充分体现了课堂的开放意识。
(2)教师出示幻灯片动画演示,让学生再一次经历对反比例函数图像的探究过程,大大激发了学生的学习和探索兴趣,同时培养学生思维的严谨性和创新性,
(3)教师引导学生区分正比例函数图像的连续性(经过)和反比例函数图像的不连续性(位于)。
探究活动(二)
通过前面的探究,我们得出了反比例函数的图像和k值正负之间关系的同时,我们又会很自然的想到对于反比例函数,当k的值分别为
k>0和
k<0时,
随着x的增大,y
的值又会有什么样的变化呢?
活动过程
(1)教师出示幻灯片动画,通过点的运动轨迹,使学生能够更加直观、形象的了解反比例函数的图像,y随x的变化而变化的规律。
(2)学生归纳反比例函数图像中,当k>0时,在每个象限内,y随x的增大而减小,
当k<0时,在每个象限内,y随x的增大而增大的过程。
设计意图:
观察是得出结论的有效途径,学生通过观察动画,小组合作探究、互相交流,让学生自由发言,充分发挥学生的积极主动性,不仅锻炼了学生的分析问题能力,同时更尊重了个体的展示,提供互助互补的平台,使学生既得到了自主发展,又培养了合作精神、创新意识,课堂气氛进入了高潮。
(四)跟踪训练,巩固新知:
1、已知反比例函数
的图像在第二、四象限内,则m的取值范围( )
A.
m
≥
5
B.
m
>
5
C
.
m
≤5
D.
m
<
5
2
、对于反比例函数 ,当x<0时,函数的这部分图像位于第
象限.
3
、如果反比例函数
的图像位于第一三象限内,那么k
(填“>0”或“<0”)且这两个分支在各自的象限内随着x的增大,y的值随之
(填“增大”或“减小”)
设计意图:
上面的三道题主要针对本节课的内容,重点考查学生对于k的正负性与图像所在象限以及y随x的变化而变化的关系,发展学生正确的解题思路和数形结合的思想意识。
4、函数y=kx
()与
()
在同一坐标系中的图像可能是(
)
设计意图:本题重点考查学生观察函数图像及对函数表达式的综合理解及运用能力
(五)当堂检测
拓展延伸:
2.若反比例函数
y=
,(x1,y1)(x2,y2)为图像上的两点,若0y2.则k的取值范围
设计意图:
作业设计具有开放性和对课堂知识
的拓展性,同时又具有实践性,是从不同角度对所学
知识的再现与提高;并使学生从中体会到知识的无穷
变化给我们带来的无限乐趣。
3、已知,
如图所示,A(
x1,
y1
)、
B(
x2
,
y2)、C
(
x3,
y3
)是反比例
函数
的图像在第一象限的分支
上的三点,
且
x1
<
x2
<
x3
。
(1)比较
y1,
y2
,
y3
的大小;
(2)过A、B、C三点分别作两坐标轴
的垂线,D、E、F
和
H、N、P
是垂足,矩形ADOH,
矩形BEON,矩形CFOP
的面积S1、S2
、
S3的大小关系是什么?为什么?
设计意图:
本题主要是在考查学生反比例函数的图像及解析式的基础上,利用图形的面积引导学生分析发现常数k的值与变量x、y之间的关系,是对函数性质的灵活运用。
挑战中考:(2012年河北中考)
如图12,四边形是平行四边形,点.反比例函数的图象经过点,点是一次函数的图象与该反比例函数图象的一个公共点.
(1)求反比例函数的解析式;
(2)通过计算,说明一次函数的图象一定过点;
(3)对于一次函数,当的增大而增大时,确定点横坐标的取值范围(不必写出过程).
设计意图:
本题主要是考察学生综合运用知识的能力,提战中考题,激发学习兴趣。
(五)回顾反思,交流总结:
愉悦的学习氛围,认真的观察,紧张的探究,和谐的交流,最终通过不懈的努力,我们可以得到反比例函数的哪些具体性质呢?
设计意图:
在知识小结中,我注重引导学生从内容、方法到获取知识的途径,全方面,多角度地回顾探究规律的过程。这时学生兴趣高涨,积极主动地举手回答,气氛非常活跃,他们争先恐后的交流,归纳,概括规律。
这时教师出示多媒体课件演示,使学生在轻松愉悦的氛围中知道:
对于反比例函数,当k
>
0时,
图像的两个分支分别位于第一、三象限,在每个象限内,
y随x的增大而减小;
当k
<
0时,
图像的两个分支分别位于第二、四象限,
在每个象限内,
y随x的增大而增大.
这一基本规律。建立了符合个人特点的知识结构,锻炼学生的表达能力,发展学生数形结合的思想和应用数学知识的意识和能力。
板书设计:
27.2反比例函数的图像和性质
当k
>
0时,
图像的两个分支分别位于第一、三象限,
在每个象限内,
y随x的增大而减小;
1.反比例函数
当k
<
0时,
图像的两个分支分别位于第二、四象限,
在每个象限内,
y随x的增大而增大.
2.图形表示为:
k的符号
图像所在象限
函数值的增减性
教学反思:
1、通过对一次函数和正比例函数的复习,类比研究一次函数和正比例函数的性质的方法,研究反比例函数的性质,并区分正比例函数图像与性质和反比例函数图像与性质的不同。
2、通过学生动手画反比例函数图像,结合图像,归纳反比例函数的性质与图像的密切联系。由性质能确定函数图象的走向,由图像能归纳性质。充分体现数形结合的思想,又发展了学生分析、归纳的能力。
3、设计不同的题型,满足不同层次学生的需要。
4、最后的中考题,让学生发现中考题并不是难,只要我们把基础知识和基本方法掌握,很容易得高分。减轻学生的压力。
2
4
6
-2
-4
-6
4
-2
2
6
-4
-6
0
x
y
2
4
6
-2
-4
-6
4
-2
2
6
-4
-6
0
y
x
2
4
6
-2
-4
-6
4
-2
2
6
-4
-6
0
x
y
2
4
6
-2
-4
-6
4
-2
2
6
-4
-6
0
x
y
x
A
y
o
B
x
y
o
C
x
y
o
D
x
y
o
?
x
y
P
H
N
O
D
E
F
A
B
C
数形
结合
一.教材分析:
1.教材所处的地位和作用:
本节课是在前面学习了建立反比例函数模型,确定反比例函数的表达式以及经历画反比例函数图像的过程的基础上,把反比例函数的表达式及图像有机地结合在一起,探索并理解反比例函数的性质,是对前面两节内容的归纳和概括,既体现了数形结合的思想,又发展了学生分析、归纳的能力。
2.教学目标:
(1)、知识与技能:通过反比例函数的表达式及图像的确立,经历探索反比例函数性质的过程,理解并掌握反比例函数的性质。
(2)、过程与方法:通过探索反比例函数性质的过程,培养观察、分析、归纳和概括的能力,提高从图像中获取信息的能力。
(3)、情感态度与价值观:通过感受反比例函数图像变化的乐趣,培养学生学习的毅力和信心。
3.教学重点:
本节课的教学重点为:归纳概括出图像位置及y随x的变化规律与常数k的关系,发展学生数形结合的思想。
4.教学难点:
对反比例函数性质全面、深入的理解以及应用性质解决实际问题,注重函数观念的形成,培养数学应用能力。
二.教法、学法:
1.教法分析:
本课是一节典型的通过观察反比例函数图像来归纳反比例函数性质的探究课,为突出重点,有效的突破难点,结合本节课的内容,我在教法设计上:以观察、探究、归纳法为主,辅以启发式教学和情感教学;教学手段上:以多媒体为教学平台,用形象的动画和生动的语言激发学生的学习兴趣,不断创设情境,层层深入,互动交流,使学生积极主动地参与到活动中来,成为学习的主体。
2.学法指导:
本节课在充分发挥学生主体地位的基础上进行学法指导,关注学生观察、探究过程,关注学生归纳,总结的规律,在交流中获得自己对数学知识的方法和能力,增强学生数学学习的信心。
三.教学程序:
(一)旧知回顾,提出问题:
我们已经学习了正比例函数的图像和性质,同学们还记得吗?
设计意图:由于本节课内容的特点,要想学好本节课,必须要正确处理好知识的衔接,所以,我在这个环节设置了正比例函数图像性质的复习知识,并以形象的数形结合的形式展现在学生的眼前,把枯燥的数学知识增加了无限的趣味,抓住了学生的注意力,激发学生的探究欲望。
通常学习一种函数,都要由他们的图像得出性质,那么反比例函数的图像会有什么性质呢?
(二)自主学习
尝试解决
画出反比例数
,
,
,的图像
(三)合作交流,探究性质:
探究活动(一)
(观察是发现问题的前提,观察完上面的图像后)反比例函数和的图像分别位于哪两个象限内?反比例函数和的图像分别位于哪两个象限内?反比例函数的图像所在象限和
k
是正数还是负数有什么关系?
活动过程:
(1)学生结合函数图象归纳总结:反比例函数的图像当k
>0时,图像的两个分支分别位于第一、三象限内;当k
<
0时,图像的两个分支分别位于第二、四象限内这一事实,充分体现了课堂的开放意识。
(2)教师出示幻灯片动画演示,让学生再一次经历对反比例函数图像的探究过程,大大激发了学生的学习和探索兴趣,同时培养学生思维的严谨性和创新性,
(3)教师引导学生区分正比例函数图像的连续性(经过)和反比例函数图像的不连续性(位于)。
探究活动(二)
通过前面的探究,我们得出了反比例函数的图像和k值正负之间关系的同时,我们又会很自然的想到对于反比例函数,当k的值分别为
k>0和
k<0时,
随着x的增大,y
的值又会有什么样的变化呢?
活动过程
(1)教师出示幻灯片动画,通过点的运动轨迹,使学生能够更加直观、形象的了解反比例函数的图像,y随x的变化而变化的规律。
(2)学生归纳反比例函数图像中,当k>0时,在每个象限内,y随x的增大而减小,
当k<0时,在每个象限内,y随x的增大而增大的过程。
设计意图:
观察是得出结论的有效途径,学生通过观察动画,小组合作探究、互相交流,让学生自由发言,充分发挥学生的积极主动性,不仅锻炼了学生的分析问题能力,同时更尊重了个体的展示,提供互助互补的平台,使学生既得到了自主发展,又培养了合作精神、创新意识,课堂气氛进入了高潮。
(四)跟踪训练,巩固新知:
1、已知反比例函数
的图像在第二、四象限内,则m的取值范围( )
A.
m
≥
5
B.
m
>
5
C
.
m
≤5
D.
m
<
5
2
、对于反比例函数 ,当x<0时,函数的这部分图像位于第
象限.
3
、如果反比例函数
的图像位于第一三象限内,那么k
(填“>0”或“<0”)且这两个分支在各自的象限内随着x的增大,y的值随之
(填“增大”或“减小”)
设计意图:
上面的三道题主要针对本节课的内容,重点考查学生对于k的正负性与图像所在象限以及y随x的变化而变化的关系,发展学生正确的解题思路和数形结合的思想意识。
4、函数y=kx
()与
()
在同一坐标系中的图像可能是(
)
设计意图:本题重点考查学生观察函数图像及对函数表达式的综合理解及运用能力
(五)当堂检测
拓展延伸:
2.若反比例函数
y=
,(x1,y1)(x2,y2)为图像上的两点,若0
设计意图:
作业设计具有开放性和对课堂知识
的拓展性,同时又具有实践性,是从不同角度对所学
知识的再现与提高;并使学生从中体会到知识的无穷
变化给我们带来的无限乐趣。
3、已知,
如图所示,A(
x1,
y1
)、
B(
x2
,
y2)、C
(
x3,
y3
)是反比例
函数
的图像在第一象限的分支
上的三点,
且
x1
<
x2
<
x3
。
(1)比较
y1,
y2
,
y3
的大小;
(2)过A、B、C三点分别作两坐标轴
的垂线,D、E、F
和
H、N、P
是垂足,矩形ADOH,
矩形BEON,矩形CFOP
的面积S1、S2
、
S3的大小关系是什么?为什么?
设计意图:
本题主要是在考查学生反比例函数的图像及解析式的基础上,利用图形的面积引导学生分析发现常数k的值与变量x、y之间的关系,是对函数性质的灵活运用。
挑战中考:(2012年河北中考)
如图12,四边形是平行四边形,点.反比例函数的图象经过点,点是一次函数的图象与该反比例函数图象的一个公共点.
(1)求反比例函数的解析式;
(2)通过计算,说明一次函数的图象一定过点;
(3)对于一次函数,当的增大而增大时,确定点横坐标的取值范围(不必写出过程).
设计意图:
本题主要是考察学生综合运用知识的能力,提战中考题,激发学习兴趣。
(五)回顾反思,交流总结:
愉悦的学习氛围,认真的观察,紧张的探究,和谐的交流,最终通过不懈的努力,我们可以得到反比例函数的哪些具体性质呢?
设计意图:
在知识小结中,我注重引导学生从内容、方法到获取知识的途径,全方面,多角度地回顾探究规律的过程。这时学生兴趣高涨,积极主动地举手回答,气氛非常活跃,他们争先恐后的交流,归纳,概括规律。
这时教师出示多媒体课件演示,使学生在轻松愉悦的氛围中知道:
对于反比例函数,当k
>
0时,
图像的两个分支分别位于第一、三象限,在每个象限内,
y随x的增大而减小;
当k
<
0时,
图像的两个分支分别位于第二、四象限,
在每个象限内,
y随x的增大而增大.
这一基本规律。建立了符合个人特点的知识结构,锻炼学生的表达能力,发展学生数形结合的思想和应用数学知识的意识和能力。
板书设计:
27.2反比例函数的图像和性质
当k
>
0时,
图像的两个分支分别位于第一、三象限,
在每个象限内,
y随x的增大而减小;
1.反比例函数
当k
<
0时,
图像的两个分支分别位于第二、四象限,
在每个象限内,
y随x的增大而增大.
2.图形表示为:
k的符号
图像所在象限
函数值的增减性
教学反思:
1、通过对一次函数和正比例函数的复习,类比研究一次函数和正比例函数的性质的方法,研究反比例函数的性质,并区分正比例函数图像与性质和反比例函数图像与性质的不同。
2、通过学生动手画反比例函数图像,结合图像,归纳反比例函数的性质与图像的密切联系。由性质能确定函数图象的走向,由图像能归纳性质。充分体现数形结合的思想,又发展了学生分析、归纳的能力。
3、设计不同的题型,满足不同层次学生的需要。
4、最后的中考题,让学生发现中考题并不是难,只要我们把基础知识和基本方法掌握,很容易得高分。减轻学生的压力。
2
4
6
-2
-4
-6
4
-2
2
6
-4
-6
0
x
y
2
4
6
-2
-4
-6
4
-2
2
6
-4
-6
0
y
x
2
4
6
-2
-4
-6
4
-2
2
6
-4
-6
0
x
y
2
4
6
-2
-4
-6
4
-2
2
6
-4
-6
0
x
y
x
A
y
o
B
x
y
o
C
x
y
o
D
x
y
o
?
x
y
P
H
N
O
D
E
F
A
B
C
数形
结合
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
