微专题五 一次函数的综合应用(含答案)
文档属性
| 名称 | 微专题五 一次函数的综合应用(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 314.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-16 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
沪科版数学八年级上册微专题训练
微专题五 一次函数的综合应用
类型一 一次函数与工程问题
1. 甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)乙队开挖到30m时,用了 h.开挖6h时,甲队比乙队多挖了 m;
(2)请你求出:
①甲队在0≤x≤6的时段内,y与x之间的函数关系式;
②乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(3)当x为何值时,甲、乙两队在施工过程中所挖河渠的长度相等?
类型二 一次函数与行程问题
2. 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发.不久,第二列快车也从甲地发往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分后,第二列快车与慢车相遇.设慢车行驶的时间为x(单位:时),慢车与第一、第二列快车之间的距离y(单位:千米)与x(单位:时)之间的函数关系如图1、图2所示,根据图象信息解答下列问题:
(1)甲、乙两地之间的距离为 千米;
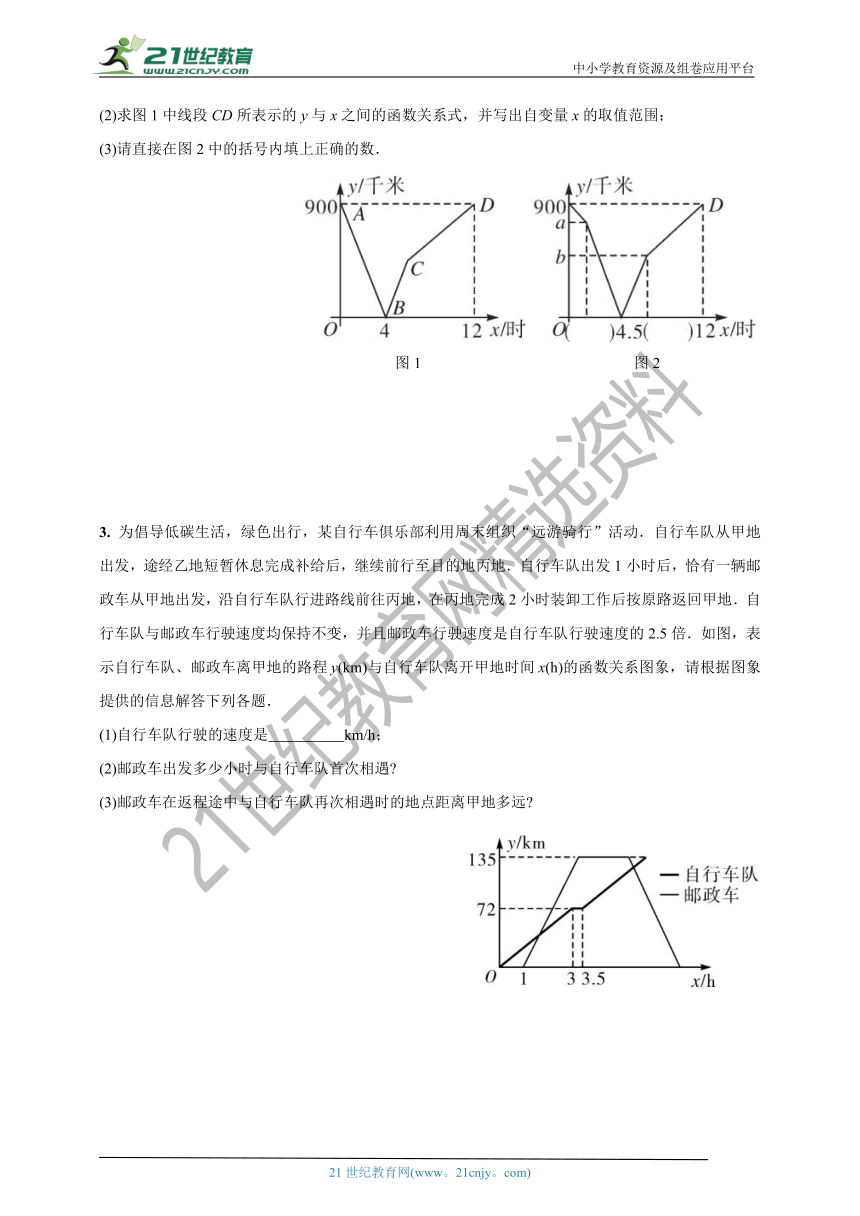
(2)求图1中线段CD所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
(3)请直接在图2中的括号内填上正确的数.
图1 图2
3. 为倡导低碳生活,绿色出行,某自行车俱乐部利用周末组织“远游骑行”活动.自行车队从甲地出发,途经乙地短暂休息完成补给后,继续前行至目的地丙地.自行车队出发1小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往丙地,在丙地完成2小时装卸工作后按原路返回甲地.自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的2.5倍.如图,表示自行车队、邮政车离甲地的路程y(km)与自行车队离开甲地时间x(h)的函数关系图象,请根据图象提供的信息解答下列各题.
(1)自行车队行驶的速度是 km/h;
(2)邮政车出发多少小时与自行车队首次相遇?
(3)邮政车在返程途中与自行车队再次相遇时的地点距离甲地多远?
类型三 一次函数与方案选择问题
4. 某社区活动中心为鼓励居民加强体育锻炼,准备购买10副某种品牌的羽毛球拍,每副球拍配x(x≥2)个羽毛球,供社区居民免费借用.该社区附近A,B两家超市都有这种品牌的羽毛球拍和羽毛球出售,且每副球拍的标价均为30元,每个羽毛球的标价均为3元,目前两家超市同时在做促销活动:A超市:所有商品均打九折(按标价的90%)销售;B超市:买一副羽毛球拍送2个羽毛球.设在A超市购买羽毛球拍和羽毛球的费用为yA(元),在B超市购买羽毛球拍和羽毛球的费用为yB(元).请解答下列问题:
(1)分别写出yA,yB与x之间的关系式;
(2)若该活动中心只在一家超市购买,你认为在哪家超市购买更划算?
(3)若每副球拍配15个羽毛球,请你帮助该活动中心设计出最省钱的购买方案.
类型四 一次函数与最低费用问题
5. 今年我市水果大丰收,A,B两个水果基地分别收获水果380件、320件,现需把这些水果全部运往甲、乙两销售点,从A基地运往甲、乙两销售点的费用分别为每件40元和20元,从B基地运往甲、乙两销售点的费用分别为每件15元和30元,现甲销售点需要水果400件,乙销售点需要水果300件.
(1)设从A基地运往甲销售点水果x件,总运费为W元,请用含x的代数式表示W,并写出x的取值范围;
(2)若总运费不超过18300元,且A地运往甲销售点的水果不低于200件,试确定运费最低的运输方案,并求出最低运费.
参考答案
1. 解:(1)2,10.
(2)①设甲队在0≤x≤6的时段y与x之间的函数关系式为y=k1x,由图可知,函数图象过点(6,60),所以6k1=60,解得k1=10,∴y=10x;②设乙队在2≤x≤6的时段内y与x之间的函数关系式为y=k2x+b,由图可知,函数图象过点(2,30),(6,50),∴ ∴ ∴y=5x+20.
(3)由题意,得10x=5x+20,解得x=4,∴当x=4h时,甲、乙两队所挖的河渠长度相等.
2. 解:(1)900
(2)慢车速度为900÷12=75(千米/时),快车速度+慢车速度=900÷4=225(千米/时),快车速度=225-75=150(千米/时),快车走完全程时间为900÷150=6(小时),快车到达时慢车与快车相距6×75=450(千米),所以C(6,450).设yCD=kx+b(k≠0,k,b为常数),把(6,450),(12,900)代入yCD=kx+b中,得 解得 所以y=75x(6≤x≤12).
(3)0.75 6.75
3. 解:(1)24
(2)2.4×2.5=60(km/h).设邮政车出发x小时与自行车队首次相遇,则60x=24(x+1),x=.答:邮政车出发小时与自行车队首次相遇.
(3)如图,
设FG:y=k1x+b1,∵F(,135),G(,0),∴ 解得 ∴y=-60x+450.设EH:y=k2x+b2,∵E(3.5,72),H(,135),∴ 解得 ∴y=24x-12.联立 解得 ∴邮政车返程与自行车再次相遇地点距甲地120km.
4. 解:(1)由题意,得yA=(10×30+3×10x)×0.9=27x+270,yB=10×30+3(10x-20)=30x+240.
(2)当yA=yB时,27x+270=30x+240,解得x=10;当yA>yB时,27x+270>30x+240,解得x<10;当yA<yB时,27x+270<30x+240,解得x>10.∴当2≤x<10时,到B超市购买划算;当x=10时,两家超市一样划算;当x>10时,在A超市购买划算.
(3)由题意知x=15>10,∴方案一:选择A超市,yA=27×15+270=675(元).方案二:先选择B超市购买10副羽毛球拍,送20个羽毛球,花费30×2+240=300(元),然后在A超市购买剩下的羽毛球,花费(10×15-20)×3×0.9=351(元),共需要费用300+351=651(元).∵651<675,∴最佳方案是先选择B超市购买10副羽毛球拍,然后在A超市购买130个羽毛球.
5. 解:(1)依题意,列表得
A(380) B(320)
甲(400) x 400-x
乙(300) 380-x 320-(400-x)=x-80
∴W=40x+20×(380-x)+15×(400-x)+30×(x-80)=35x+11200,又 解得80≤x≤380.
(2)依题意得 解得200≤x≤202,∴x=200,201,202.∵W=35x+11200,k=35>0,∴W随x的增大而增大,∴x=200时,运费W最低,最低运费为18200元.此时运输方案如下:
A B
甲 200 200
乙 180 120
_21?????????è?????(www???21cnjy???com)_
沪科版数学八年级上册微专题训练
微专题五 一次函数的综合应用
类型一 一次函数与工程问题
1. 甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)乙队开挖到30m时,用了 h.开挖6h时,甲队比乙队多挖了 m;
(2)请你求出:
①甲队在0≤x≤6的时段内,y与x之间的函数关系式;
②乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(3)当x为何值时,甲、乙两队在施工过程中所挖河渠的长度相等?
类型二 一次函数与行程问题
2. 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发.不久,第二列快车也从甲地发往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分后,第二列快车与慢车相遇.设慢车行驶的时间为x(单位:时),慢车与第一、第二列快车之间的距离y(单位:千米)与x(单位:时)之间的函数关系如图1、图2所示,根据图象信息解答下列问题:
(1)甲、乙两地之间的距离为 千米;
(2)求图1中线段CD所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
(3)请直接在图2中的括号内填上正确的数.
图1 图2
3. 为倡导低碳生活,绿色出行,某自行车俱乐部利用周末组织“远游骑行”活动.自行车队从甲地出发,途经乙地短暂休息完成补给后,继续前行至目的地丙地.自行车队出发1小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往丙地,在丙地完成2小时装卸工作后按原路返回甲地.自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的2.5倍.如图,表示自行车队、邮政车离甲地的路程y(km)与自行车队离开甲地时间x(h)的函数关系图象,请根据图象提供的信息解答下列各题.
(1)自行车队行驶的速度是 km/h;
(2)邮政车出发多少小时与自行车队首次相遇?
(3)邮政车在返程途中与自行车队再次相遇时的地点距离甲地多远?
类型三 一次函数与方案选择问题
4. 某社区活动中心为鼓励居民加强体育锻炼,准备购买10副某种品牌的羽毛球拍,每副球拍配x(x≥2)个羽毛球,供社区居民免费借用.该社区附近A,B两家超市都有这种品牌的羽毛球拍和羽毛球出售,且每副球拍的标价均为30元,每个羽毛球的标价均为3元,目前两家超市同时在做促销活动:A超市:所有商品均打九折(按标价的90%)销售;B超市:买一副羽毛球拍送2个羽毛球.设在A超市购买羽毛球拍和羽毛球的费用为yA(元),在B超市购买羽毛球拍和羽毛球的费用为yB(元).请解答下列问题:
(1)分别写出yA,yB与x之间的关系式;
(2)若该活动中心只在一家超市购买,你认为在哪家超市购买更划算?
(3)若每副球拍配15个羽毛球,请你帮助该活动中心设计出最省钱的购买方案.
类型四 一次函数与最低费用问题
5. 今年我市水果大丰收,A,B两个水果基地分别收获水果380件、320件,现需把这些水果全部运往甲、乙两销售点,从A基地运往甲、乙两销售点的费用分别为每件40元和20元,从B基地运往甲、乙两销售点的费用分别为每件15元和30元,现甲销售点需要水果400件,乙销售点需要水果300件.
(1)设从A基地运往甲销售点水果x件,总运费为W元,请用含x的代数式表示W,并写出x的取值范围;
(2)若总运费不超过18300元,且A地运往甲销售点的水果不低于200件,试确定运费最低的运输方案,并求出最低运费.
参考答案
1. 解:(1)2,10.
(2)①设甲队在0≤x≤6的时段y与x之间的函数关系式为y=k1x,由图可知,函数图象过点(6,60),所以6k1=60,解得k1=10,∴y=10x;②设乙队在2≤x≤6的时段内y与x之间的函数关系式为y=k2x+b,由图可知,函数图象过点(2,30),(6,50),∴ ∴ ∴y=5x+20.
(3)由题意,得10x=5x+20,解得x=4,∴当x=4h时,甲、乙两队所挖的河渠长度相等.
2. 解:(1)900
(2)慢车速度为900÷12=75(千米/时),快车速度+慢车速度=900÷4=225(千米/时),快车速度=225-75=150(千米/时),快车走完全程时间为900÷150=6(小时),快车到达时慢车与快车相距6×75=450(千米),所以C(6,450).设yCD=kx+b(k≠0,k,b为常数),把(6,450),(12,900)代入yCD=kx+b中,得 解得 所以y=75x(6≤x≤12).
(3)0.75 6.75
3. 解:(1)24
(2)2.4×2.5=60(km/h).设邮政车出发x小时与自行车队首次相遇,则60x=24(x+1),x=.答:邮政车出发小时与自行车队首次相遇.
(3)如图,
设FG:y=k1x+b1,∵F(,135),G(,0),∴ 解得 ∴y=-60x+450.设EH:y=k2x+b2,∵E(3.5,72),H(,135),∴ 解得 ∴y=24x-12.联立 解得 ∴邮政车返程与自行车再次相遇地点距甲地120km.
4. 解:(1)由题意,得yA=(10×30+3×10x)×0.9=27x+270,yB=10×30+3(10x-20)=30x+240.
(2)当yA=yB时,27x+270=30x+240,解得x=10;当yA>yB时,27x+270>30x+240,解得x<10;当yA<yB时,27x+270<30x+240,解得x>10.∴当2≤x<10时,到B超市购买划算;当x=10时,两家超市一样划算;当x>10时,在A超市购买划算.
(3)由题意知x=15>10,∴方案一:选择A超市,yA=27×15+270=675(元).方案二:先选择B超市购买10副羽毛球拍,送20个羽毛球,花费30×2+240=300(元),然后在A超市购买剩下的羽毛球,花费(10×15-20)×3×0.9=351(元),共需要费用300+351=651(元).∵651<675,∴最佳方案是先选择B超市购买10副羽毛球拍,然后在A超市购买130个羽毛球.
5. 解:(1)依题意,列表得
A(380) B(320)
甲(400) x 400-x
乙(300) 380-x 320-(400-x)=x-80
∴W=40x+20×(380-x)+15×(400-x)+30×(x-80)=35x+11200,又 解得80≤x≤380.
(2)依题意得 解得200≤x≤202,∴x=200,201,202.∵W=35x+11200,k=35>0,∴W随x的增大而增大,∴x=200时,运费W最低,最低运费为18200元.此时运输方案如下:
A B
甲 200 200
乙 180 120
_21?????????è?????(www???21cnjy???com)_
