微专题六 证明三角形全等的基本思路归纳(含答案)
文档属性
| 名称 | 微专题六 证明三角形全等的基本思路归纳(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 292.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-16 09:22:36 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
沪科版数学八年级上册微专题训练
微专题六 证明三角形全等的基本思路归纳
类型一 已知两边对应相等
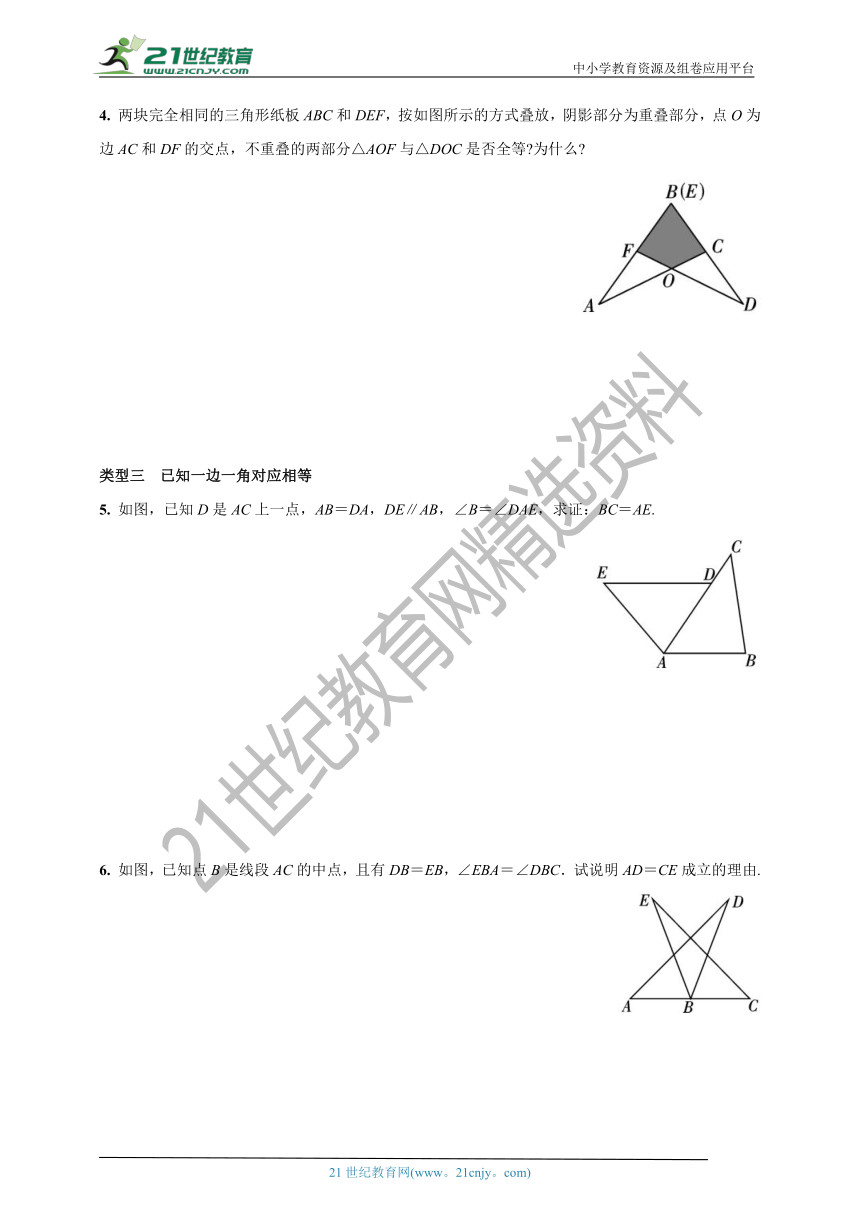
1. 如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E.
2. 如图,AB=AD,AC=AE,∠BAD=∠CAE.求证:BC=DE.
.
类型二 已知两角对应相等
3. 如图,已知AB=AE,∠1=∠2,∠B=∠E,求证:BC=ED.
4. 两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O为边AC和DF的交点,不重叠的两部分△AOF与△DOC是否全等?为什么?
类型三 已知一边一角对应相等
5. 如图,已知D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE,求证:BC=AE.
6. 如图,已知点B是线段AC的中点,且有DB=EB,∠EBA=∠DBC.试说明AD=CE成立的理由.
7. 已知AE交BC于点D,∠1=∠2=∠3,AB=AD.
求证:(1)∠ADC=∠ABE;
(2)DC=BE.
类型四 全等基本图形归纳(平移、翻折、旋转)
8. 如图,Rt△ABC中,∠C=90°,将△ABC沿AB向下翻折后,再绕点A按顺时针方向旋转α度(α<∠BAC),得到Rt△ADE,其中斜边AE交BC于点F,直角边DE分别交AB,BC于点G,H.
(1)请根据题意用实线补全图形;
(2)求证:△AFB≌△AGE.
9. 如图,点B,C,E,F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.
求证:(1)△ABC≌△DEF;
(2)AB∥DE.
10. 如图,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
参考答案
1. 证明:∵AB∥CD,∴∠BAC=∠ECD.在△ABC和△CED中, ∴△ABC≌△CED,(SAS) ∴∠B=∠E.
2. 证明:∵∠BAD=∠CAE,∴∠BAD+∠DAC=∠CAE+∠DAC,即∠BAC=∠DAE.又∵AB=AD,AC=AE,∴△ABC≌△ADE(SAS),∴BC=DE.
3. 证明:∵∠1=∠2,∴∠1+∠BAD=∠2+∠BAD,即∠EAD=∠BAC.在△AED与△ABC中, ∴△AED≌△ABC.(ASA) ∴BC=ED.
4. 解:全等,理由如下:∵两块三角形纸板完全相同,∴BC=BF,AB=BD,∠A=∠D,∴AB-BF=BD-BC,即AF=DC.又∵∠AOF=∠DOC,∴△AOF≌△DOC.(AAS)
5. 证明:∵DE∥AB,∴∠CAB=∠ADE,又∵AB=DA,∠B=∠DAE,∴△ABC≌△DAE,(ASA) ∴BC=AE.
6. 解:∵点B是线段AC的中点.∴AB=CB.又∵∠EBA=∠DBC,∴∠DBE+∠EBA=∠DBE+∠DBC,即∠DBA=∠EBC.在△ABD和△CBE中, ∴△ABD≌△CBE,(SAS) ∴AD=CE.
7. 证明:(1)∵∠ADC=∠4+∠2,∠ABE=∠4+∠3,且∠2=∠3,∴∠ADC=∠ABE.
(2)在△ADC和△ABE中, ∴△ADC≌△ABE,(ASA) ∴DC=BE.
8. 解:(1)补图略
(2)证明:由题意得△ABC≌△AED,∴AB=AE,∠ABC=∠E,又∵∠α=∠α,∴△AFB≌△AGE.(ASA)
9. 证明:(1)∵AC⊥BC于点C,DF⊥EF于点F,∴∠ACB=∠DFE=90°.在△ABC和△DEF中, ∴△ABC≌△DEF(SAS).
(2)由(1)可知△ABC≌△DEF,∴∠B=∠DEF,∴AB∥DE.
10. 解:DE+BF=EF.证明如下:延长CB至G,使BG=DE.∵将Rt△ABC沿斜边翻折得到△ADC,∴AD=AB,在△AGB和△AED中, ∴△AGB≌△AED.(SAS) ∴∠BAG=∠DAE,AG=AE.∵∠EAF=∠DAB,∴∠DAE+∠BAF=∠EAF.又∵∠DAE+∠BAF=∠BAG+∠BAF=∠GAF,∴∠GAF=∠EAF.在△AGF和△AEF中, ∴△AGF≌△AEF.(SAS) ∴GF=EF.又GF=GB+BF,GB=DE,∴EF=DE+BF.
_21?????????è?????(www???21cnjy???com)_
沪科版数学八年级上册微专题训练
微专题六 证明三角形全等的基本思路归纳
类型一 已知两边对应相等
1. 如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E.
2. 如图,AB=AD,AC=AE,∠BAD=∠CAE.求证:BC=DE.
.
类型二 已知两角对应相等
3. 如图,已知AB=AE,∠1=∠2,∠B=∠E,求证:BC=ED.
4. 两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O为边AC和DF的交点,不重叠的两部分△AOF与△DOC是否全等?为什么?
类型三 已知一边一角对应相等
5. 如图,已知D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE,求证:BC=AE.
6. 如图,已知点B是线段AC的中点,且有DB=EB,∠EBA=∠DBC.试说明AD=CE成立的理由.
7. 已知AE交BC于点D,∠1=∠2=∠3,AB=AD.
求证:(1)∠ADC=∠ABE;
(2)DC=BE.
类型四 全等基本图形归纳(平移、翻折、旋转)
8. 如图,Rt△ABC中,∠C=90°,将△ABC沿AB向下翻折后,再绕点A按顺时针方向旋转α度(α<∠BAC),得到Rt△ADE,其中斜边AE交BC于点F,直角边DE分别交AB,BC于点G,H.
(1)请根据题意用实线补全图形;
(2)求证:△AFB≌△AGE.
9. 如图,点B,C,E,F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.
求证:(1)△ABC≌△DEF;
(2)AB∥DE.
10. 如图,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
参考答案
1. 证明:∵AB∥CD,∴∠BAC=∠ECD.在△ABC和△CED中, ∴△ABC≌△CED,(SAS) ∴∠B=∠E.
2. 证明:∵∠BAD=∠CAE,∴∠BAD+∠DAC=∠CAE+∠DAC,即∠BAC=∠DAE.又∵AB=AD,AC=AE,∴△ABC≌△ADE(SAS),∴BC=DE.
3. 证明:∵∠1=∠2,∴∠1+∠BAD=∠2+∠BAD,即∠EAD=∠BAC.在△AED与△ABC中, ∴△AED≌△ABC.(ASA) ∴BC=ED.
4. 解:全等,理由如下:∵两块三角形纸板完全相同,∴BC=BF,AB=BD,∠A=∠D,∴AB-BF=BD-BC,即AF=DC.又∵∠AOF=∠DOC,∴△AOF≌△DOC.(AAS)
5. 证明:∵DE∥AB,∴∠CAB=∠ADE,又∵AB=DA,∠B=∠DAE,∴△ABC≌△DAE,(ASA) ∴BC=AE.
6. 解:∵点B是线段AC的中点.∴AB=CB.又∵∠EBA=∠DBC,∴∠DBE+∠EBA=∠DBE+∠DBC,即∠DBA=∠EBC.在△ABD和△CBE中, ∴△ABD≌△CBE,(SAS) ∴AD=CE.
7. 证明:(1)∵∠ADC=∠4+∠2,∠ABE=∠4+∠3,且∠2=∠3,∴∠ADC=∠ABE.
(2)在△ADC和△ABE中, ∴△ADC≌△ABE,(ASA) ∴DC=BE.
8. 解:(1)补图略
(2)证明:由题意得△ABC≌△AED,∴AB=AE,∠ABC=∠E,又∵∠α=∠α,∴△AFB≌△AGE.(ASA)
9. 证明:(1)∵AC⊥BC于点C,DF⊥EF于点F,∴∠ACB=∠DFE=90°.在△ABC和△DEF中, ∴△ABC≌△DEF(SAS).
(2)由(1)可知△ABC≌△DEF,∴∠B=∠DEF,∴AB∥DE.
10. 解:DE+BF=EF.证明如下:延长CB至G,使BG=DE.∵将Rt△ABC沿斜边翻折得到△ADC,∴AD=AB,在△AGB和△AED中, ∴△AGB≌△AED.(SAS) ∴∠BAG=∠DAE,AG=AE.∵∠EAF=∠DAB,∴∠DAE+∠BAF=∠EAF.又∵∠DAE+∠BAF=∠BAG+∠BAF=∠GAF,∴∠GAF=∠EAF.在△AGF和△AEF中, ∴△AGF≌△AEF.(SAS) ∴GF=EF.又GF=GB+BF,GB=DE,∴EF=DE+BF.
_21?????????è?????(www???21cnjy???com)_
