立方根
图片预览








文档简介
(共24张PPT)
汶上县第二实验中学
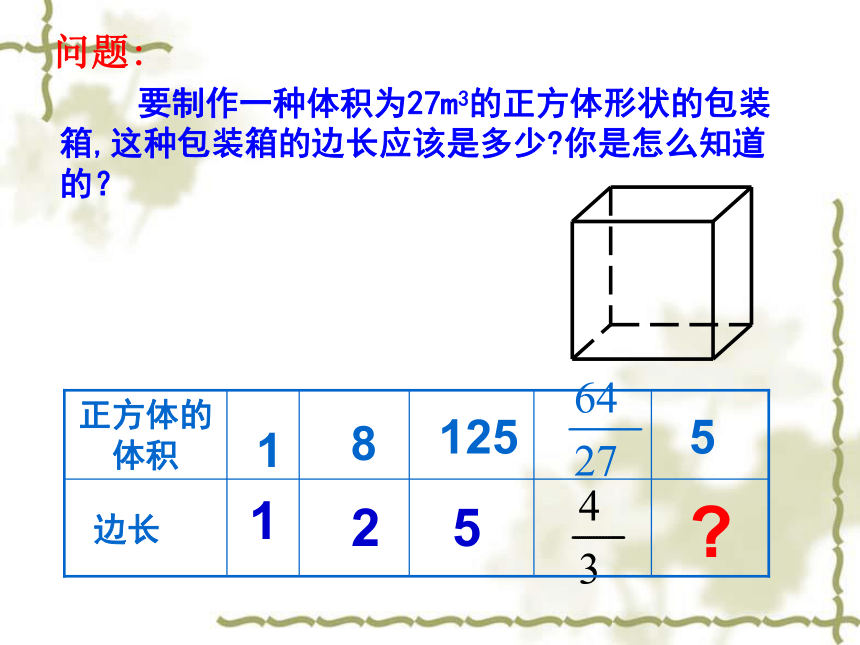
要制作一种体积为27m3的正方体形状的包装箱,这种包装箱的边长应该是多少 你是怎么知道的?
问题:
1
2
5
5
正方体的体积
1
边长
8
125
1.什么叫平方根?如何用符号表示数a (a≥0 )的平方根
2.正数有几个平方根?它们之间的关系是什么?负数有没有平方根?0的平方根是什么
3.开平方是如何定义的?开平方和平方之间是什么关系
一般地,如果一个数的立方等于a,那么这个数就叫做a的立方根或三次方根.
用式子表示,如果x3 =a,那么x叫做a的立方根.
立方根的定义:
用什么符号表示
立方根?
数的立方根与平方根有什么不同?
探究
根据立方根的意义填空,看看正数,0和负数的立方根
各有什么特点?
因为23=8,所以8的立方根是( );
因为( )3=0.125,所以0.125的立方根是( );
因为( )3=0,所以0的立方根是( );
因为( )3=-8,所以-8的立方根是( );
因为( )3=-0.125,所以-0.125的立方根是( ).
2
-0.5
-2
-2
0
0
0.5
0.5
-0.5
求一个数的立方根的运算,叫做开立方.
开立方:
开立方与立方也是互为逆运算。
立方根的性质 正数的立方根是一个正数;负数的立方根是一个负数;零的立方根是零.
立方根的表示方法:
其中: a 称为被开方数;
3 称为根指数.
读作: 三次根号 a ;
结论:一个数的立方根是唯一的.
(1)-27 (2) (3)-0.216 (5) -5
例1 求下列各数的立方根:
例2 求下列各式的值:
; (2) ;
(3) ;(4) .
例3 求下列各式中x的值:
(1)
(3)
(2)
求下列各组数的值
(1) , ;
(2) , ;
(3) , .
你能得出什么结论?
探究一
探究二
求 , , , ,
的值,你能得出什么结论?
求 , , , ,
的值,你能得出什么结论?
探究三
1.判断下列说法是否正确,并说明理由
(1)
x
(2) 25的平方根是5
x
(3) -64没有立方根
x
√
(5) (-4)3的立方根是-4
(4) -0.5是-0.125的立方根
√
x
2.填空:
(1)64的平方根是________,64的立方根是________.
(2)-216的立方根是________.
(3)若 ,则x=________.
(4) 的立方根是________.
(5)如果一个数的平方根与立方根相同,则这个数是________.
(6)如果一个数的立方根是这个数的本身,那么这个数是________.
(2) 的立方根是________.
(3) 的立方根是_______.
(4)若 ,则 x=_______.
若 ,则 x=________.
-6
±8
4
27
0
0,1,-1
3.求下列各式的值:
(1)
(4)
(3)
(2)
1
2
5
4
3
立方根是它本身的数有哪些
有1, -1, 0
平方根是它本身的数呢
只有0
算术平方根是它本身的数呢
有1、0
将体积分别为600cm3和129cm3的长方体铁块,熔成一个正方体铁块,那么这个正方体的边长是多少?
求下列各式的值:
10
-0.1
0.2
-0.2
2
若 ,
求 的值.
已知的 平方根是 ,
的立方根是3,
试求 的平方根。
平方根 立方根
定
义
数学语言
性
质 正
数
0
负
数
开
方
表
示
如果一个数的平方等于a,
那么这个数就叫a的平方根。
如果一个数的立方等于a,
那么这个数就叫a的立方根。
有两个平方根,互为相反数
有一个平方根,是0
没有平方根
求一个数的平方根的运算叫开平方;开平方与平方是互逆运算。
,其中a 是被开方数,
2是根指数(省略)
求一个数的立方根的运算
叫开立方;开立方与立方
是互逆运算。
有一个立方根,也是负数
有一个立方根,是0
有一个立方根,也是正数
,其中a 是被开方数,
3是根指数(不能省略)
a≥0
x2 = a
x3 = a
a任何数
比较归纳平方根与立方根的异同
作业本:
课本 80页 习题13.2 2、5、6
同步学习:
52-54页
R
r
乙
甲
已知半径为r 的球,其体积 的计 算公式为 . 如果甲、乙两球 体积的比为1 :8,则甲、乙两球的半径比为 .
1 2
:
挑战极限
汶上县第二实验中学
要制作一种体积为27m3的正方体形状的包装箱,这种包装箱的边长应该是多少 你是怎么知道的?
问题:
1
2
5
5
正方体的体积
1
边长
8
125
1.什么叫平方根?如何用符号表示数a (a≥0 )的平方根
2.正数有几个平方根?它们之间的关系是什么?负数有没有平方根?0的平方根是什么
3.开平方是如何定义的?开平方和平方之间是什么关系
一般地,如果一个数的立方等于a,那么这个数就叫做a的立方根或三次方根.
用式子表示,如果x3 =a,那么x叫做a的立方根.
立方根的定义:
用什么符号表示
立方根?
数的立方根与平方根有什么不同?
探究
根据立方根的意义填空,看看正数,0和负数的立方根
各有什么特点?
因为23=8,所以8的立方根是( );
因为( )3=0.125,所以0.125的立方根是( );
因为( )3=0,所以0的立方根是( );
因为( )3=-8,所以-8的立方根是( );
因为( )3=-0.125,所以-0.125的立方根是( ).
2
-0.5
-2
-2
0
0
0.5
0.5
-0.5
求一个数的立方根的运算,叫做开立方.
开立方:
开立方与立方也是互为逆运算。
立方根的性质 正数的立方根是一个正数;负数的立方根是一个负数;零的立方根是零.
立方根的表示方法:
其中: a 称为被开方数;
3 称为根指数.
读作: 三次根号 a ;
结论:一个数的立方根是唯一的.
(1)-27 (2) (3)-0.216 (5) -5
例1 求下列各数的立方根:
例2 求下列各式的值:
; (2) ;
(3) ;(4) .
例3 求下列各式中x的值:
(1)
(3)
(2)
求下列各组数的值
(1) , ;
(2) , ;
(3) , .
你能得出什么结论?
探究一
探究二
求 , , , ,
的值,你能得出什么结论?
求 , , , ,
的值,你能得出什么结论?
探究三
1.判断下列说法是否正确,并说明理由
(1)
x
(2) 25的平方根是5
x
(3) -64没有立方根
x
√
(5) (-4)3的立方根是-4
(4) -0.5是-0.125的立方根
√
x
2.填空:
(1)64的平方根是________,64的立方根是________.
(2)-216的立方根是________.
(3)若 ,则x=________.
(4) 的立方根是________.
(5)如果一个数的平方根与立方根相同,则这个数是________.
(6)如果一个数的立方根是这个数的本身,那么这个数是________.
(2) 的立方根是________.
(3) 的立方根是_______.
(4)若 ,则 x=_______.
若 ,则 x=________.
-6
±8
4
27
0
0,1,-1
3.求下列各式的值:
(1)
(4)
(3)
(2)
1
2
5
4
3
立方根是它本身的数有哪些
有1, -1, 0
平方根是它本身的数呢
只有0
算术平方根是它本身的数呢
有1、0
将体积分别为600cm3和129cm3的长方体铁块,熔成一个正方体铁块,那么这个正方体的边长是多少?
求下列各式的值:
10
-0.1
0.2
-0.2
2
若 ,
求 的值.
已知的 平方根是 ,
的立方根是3,
试求 的平方根。
平方根 立方根
定
义
数学语言
性
质 正
数
0
负
数
开
方
表
示
如果一个数的平方等于a,
那么这个数就叫a的平方根。
如果一个数的立方等于a,
那么这个数就叫a的立方根。
有两个平方根,互为相反数
有一个平方根,是0
没有平方根
求一个数的平方根的运算叫开平方;开平方与平方是互逆运算。
,其中a 是被开方数,
2是根指数(省略)
求一个数的立方根的运算
叫开立方;开立方与立方
是互逆运算。
有一个立方根,也是负数
有一个立方根,是0
有一个立方根,也是正数
,其中a 是被开方数,
3是根指数(不能省略)
a≥0
x2 = a
x3 = a
a任何数
比较归纳平方根与立方根的异同
作业本:
课本 80页 习题13.2 2、5、6
同步学习:
52-54页
R
r
乙
甲
已知半径为r 的球,其体积 的计 算公式为 . 如果甲、乙两球 体积的比为1 :8,则甲、乙两球的半径比为 .
1 2
:
挑战极限
