人教版九年级数学上册第二十四章 圆 24.1 圆的有关性质 练习题(word版含答案)
文档属性
| 名称 | 人教版九年级数学上册第二十四章 圆 24.1 圆的有关性质 练习题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 575.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-16 18:24:35 | ||
图片预览



文档简介
人教版九年级数学上册第二十四章
圆
24.1
圆的有关性质
练习题
一、选择题(30分)
1.如图,MN为⊙O的直径,A、B是⊙O上的两点,过A作AC⊥MN于点C,过B作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6,则PA+PB的最小值是( ).
A.20
B.
C.14
D.
2.一副学生三角板放在一个圈里恰好如图所示,顶点在圆圈外,其他几个顶点都在圆圈上,圆圈和交于点,已知,则这个圆圈上的弦长是(
)
A.
B.
C.
D.
3.如图,AB为⊙O的直径,AC=2,BC=4,CD=BD=DE,则CE=( )
A.3﹣
B.
C.
D.
4.如图,点A,B,C,D在⊙O上,弦AD的延长线与弦BC的延长线相交于点E.用①AB是⊙O的直径,②CB=CE,③AB=AE中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
A.0
B.1
C.2
D.3
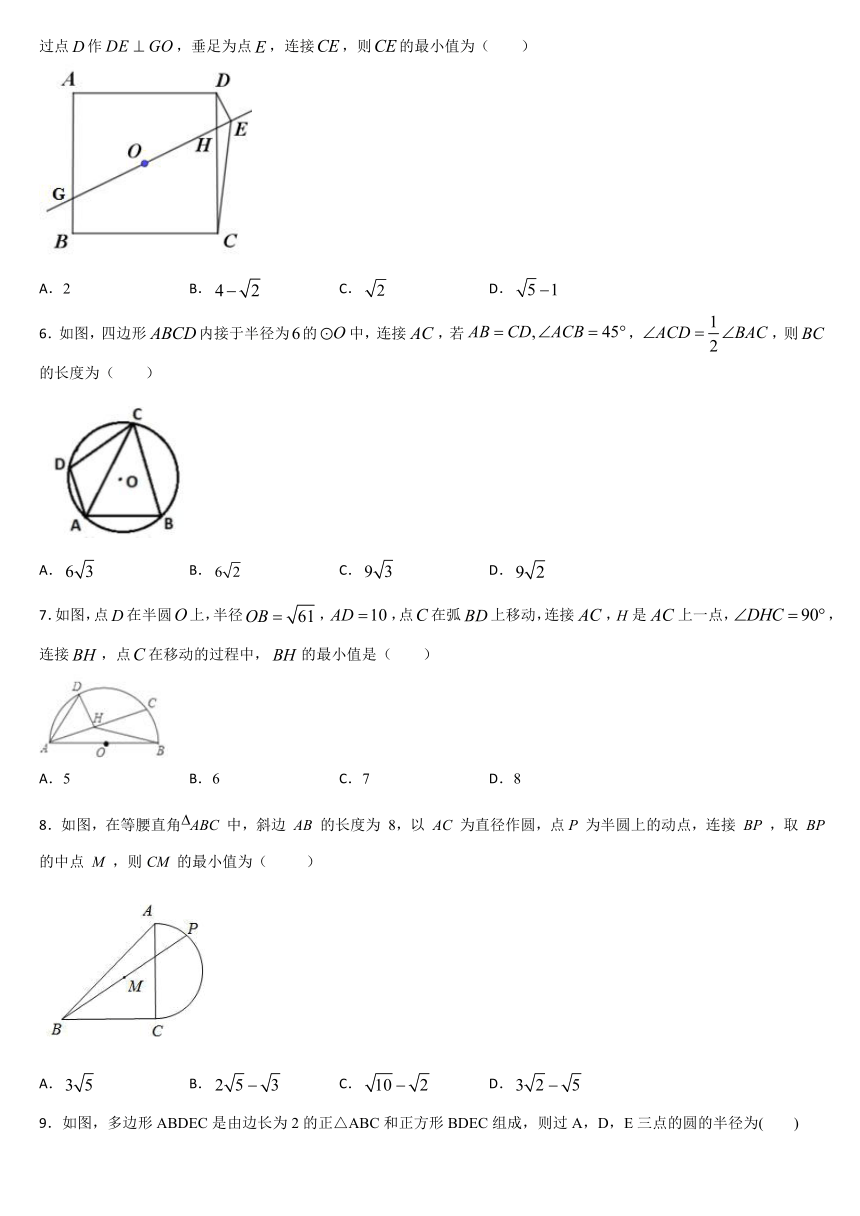
5.如图,已知正方形的边长为,点为正方形的中心,点为边上一动点,直线交于点,过点作,垂足为点,连接,则的最小值为(
)
A.2
B.
C.
D.
6.如图,四边形内接于半径为的中,连接,若,,则的长度为(
)
A.
B.
C.
D.
7.如图,点在半圆上,半径,,点在弧上移动,连接,是上一点,,连接,点在移动的过程中,的最小值是(
)
A.5
B.6
C.7
D.8
8.如图,在等腰直角ABC
中,斜边
AB
的长度为
8,以
AC
为直径作圆,点P
为半圆上的动点,连接
BP
,取
BP
的中点
M
,则CM
的最小值为(
)
A.
B.
C.
D.
9.如图,多边形ABDEC是由边长为2的正△ABC和正方形BDEC组成,则过A,D,E三点的圆的半径为(
)
A.
B.2
C.
D.
10.如图,AB是半圆O的直径,点D在半圆O上,AB=13,AD=5,C是弧BD上的一个动点,连接AC,过D点作DH⊥AC于H.连接BH,在点C移动的过程中,BH的最小值是(
)
A.
B.
C.
D.
二、填空题(15分)
11.如图,等边△ABC中,D在BC上,E在AC上,BD=CE,连BE、AD交于F,T在EF上,且DT=CE,AF=50,TE=16,则FT=_____.
12.如图,在⊙O中,是⊙O的直径,,点是点关于的对称点,是上的一动点,下列结论:①;②;③;④的最小值是10.上述结论中正确的个数是_________.
13.如图,在矩形中,是的中点,是边上一动点,将沿着翻折,使得点落在点处,矩形内有一动点连接则的最小值为_______________________.
14.如图,点I为△ABC的内心,连AI交△ABC的外接圆于点D,若,点E为弦AC的中点,连接EI,IC,若,,则IE的长为__.
15.如图,平面直角坐标系中有正方形OABC,B(4,4),动点D从B出发向C运动,动点E从A出发向B运动,且动点D、E运动的速度相同.当它们到达各自终点时停止运动,运动过程中线段OE、AD相交于点H,F是线段OC上任意一点,当BF+FH最小时,点F的坐标为_____.
三、解答题(75分)
16.已知⊙的直径为,点,点,点在⊙上,的平分线交⊙于点.
()如图①,若为⊙的直径,,求,,的长.
()如图②,若,求的长.
17.如图,在⊙O中,AB是直径,P为AB上一点,过点P作弦MN,∠NPB=45°.
(1)若AP=2,BP=6,求MN的长;
(2)若MP=3,NP=5,求AB的长;
(3)当P在AB上运动时(∠NPB=45°不变),的值是否发生变化?若不变,请求出其值;若变化,请求出其范围.
18.如图1,抛物线过点,,点为直线下方抛物线上一动点,为抛物线顶点,抛物线对称轴与直线交于点.
(1)求抛物线的表达式与顶点的坐标;
(2)在直线上是否存在点,使得,,,为顶点的四边形是平行四边形,若存在,请求出点坐标;
(3)在轴上是否存在点,使?若存在,求点的坐标;若不存在,请说明理由.
19.(问题提出)
对于给定三角形,如何求它的外接圆直径呢?
(初步思考)
对于任意三角形,可以分三类进行研究:直角三角形、锐角三角形和钝角三角形.由于直角三角形的斜边就是其外接圆的直径,故我们将研究的重点放在锐角三角形和钝角三角形上.下列研究以钝角三角形作为对象(可用类似方法研究锐角三角形).
(深入研究)
规定△ABC是钝角三角形,∠A是钝角,⊙O是△ABC的外接圆,下面分4种情况求⊙O的直径(结果需用含有各情况中表示线段或角的字母的式子表示).
(1)如图①,AB=m,∠ABC=α,∠ACB=β.
思路:连接AO并延长,交⊙O于点D,连接BD.易得△ABD是直角三角形,AB=m,∠D=∠C=β,此时可求出⊙O的直径AD的长.根据上述思路,直接写出⊙O直径的长.
(2)如图②,BC=m,∠ABC=α,∠ACB=β.
类比(1)的思路,连接CO并延长,交⊙O于点D,连接BD,则⊙O的直径为
.
(3)如图③,BC=m,AB=n,∠ABC=α.根据上述思路,直接写出⊙O直径的长.
(4)如图④,BC=a,AC=b,AB=c.根据上述思路,直接写出⊙O直径的长.
20.已知:如图1,在平面直角坐标系中,A(2,-1),以M(-1,0)为圆心,以AM为半径的圆交y轴于点B,连结BM并延长交⊙M于点C,动点P在线段BC上运动,长为的线段PQ∥x轴(点Q在点P右侧),连结AQ.
(1)求⊙M的半径长和点B的坐标;
(2)如图2,连结AC,交线段PQ于点N,
①求AC所在直线的解析式;
②当PN=QN时,求点Q的坐标;
(3)点P在线段BC上运动的过程中,请直接写出AQ的最小值和最大值.
21.阅读下面材料:
对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A被这个圆所覆盖.
对于平面图形A,如果存在两个或两个以上的圆,使图形A上的任意一点到其中某个圆的圆心的距离都不大于这个圆的半径,则称图形A被这些圆所覆盖.
例如:图1中①的三角形被一个圆覆盖,②中的四边形被两个圆所覆盖.
回答下列问题:
(1)边长为1
cm的正方形被一个半径为r的圆所覆盖,r的最小值是______
cm;
(2)边长为1
cm的等边三角形被一个半径为r的圆所覆盖,r的最小值是_____
cm;
(3)长为2
cm,宽为1
cm的矩形被两个半径均为r的圆所覆盖,r的最小值是_____
cm.这两个圆的圆心距是_____
cm..
22.已知如图,抛物线y=x2+mx+n的顶点为(1,﹣),其图象与x轴交于A,B两点,与y轴交于点C.
(1)m= ,n= ;
(2)点P在抛物线的对称轴上,当∠APC=∠BAC时,求点P的坐标;
(3)点M为线段AC的中点,点N是线段AB上的动点,在△ABC绕点C按逆时针方向旋转的过程中,点N的对应点是点N′,直接写出线段MN′长度的最大值和最小值.
23.如图,AB是⊙O的直径,C,D,E是⊙O上的点,若
,∠E=70°,求∠ABC的度数.
【参考答案】
1.B
2.C
3.D
4.D
5.D
6.A
7.D
8.C
9.B
10.C
11.17
12.3
13.
14.4
15.(0,)
16.(1)AC=8,BD=CD=5;(2)5.
17.(1);(2);(3)不变,值为
18.(1),点的坐标为(1,-4);(2)符合条件的点的坐标为,;(3)点的坐标为或.
19.(1);(2);(3);(4).
20.(1)半径为,点B(0,3);
(2)①yAC=x-2,②点Q坐标为(-,-)
(3)AQ最小值为,AQ最大值为
21.(1)
;(2);(3)
,
1.
22.(1)﹣,﹣2;(2)满足条件的点P的坐标为(1,)或(1,﹣);(3)MN'的最小值为2﹣,最大值为+2.
23.40°
圆
24.1
圆的有关性质
练习题
一、选择题(30分)
1.如图,MN为⊙O的直径,A、B是⊙O上的两点,过A作AC⊥MN于点C,过B作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6,则PA+PB的最小值是( ).
A.20
B.
C.14
D.
2.一副学生三角板放在一个圈里恰好如图所示,顶点在圆圈外,其他几个顶点都在圆圈上,圆圈和交于点,已知,则这个圆圈上的弦长是(
)
A.
B.
C.
D.
3.如图,AB为⊙O的直径,AC=2,BC=4,CD=BD=DE,则CE=( )
A.3﹣
B.
C.
D.
4.如图,点A,B,C,D在⊙O上,弦AD的延长线与弦BC的延长线相交于点E.用①AB是⊙O的直径,②CB=CE,③AB=AE中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
A.0
B.1
C.2
D.3
5.如图,已知正方形的边长为,点为正方形的中心,点为边上一动点,直线交于点,过点作,垂足为点,连接,则的最小值为(
)
A.2
B.
C.
D.
6.如图,四边形内接于半径为的中,连接,若,,则的长度为(
)
A.
B.
C.
D.
7.如图,点在半圆上,半径,,点在弧上移动,连接,是上一点,,连接,点在移动的过程中,的最小值是(
)
A.5
B.6
C.7
D.8
8.如图,在等腰直角ABC
中,斜边
AB
的长度为
8,以
AC
为直径作圆,点P
为半圆上的动点,连接
BP
,取
BP
的中点
M
,则CM
的最小值为(
)
A.
B.
C.
D.
9.如图,多边形ABDEC是由边长为2的正△ABC和正方形BDEC组成,则过A,D,E三点的圆的半径为(
)
A.
B.2
C.
D.
10.如图,AB是半圆O的直径,点D在半圆O上,AB=13,AD=5,C是弧BD上的一个动点,连接AC,过D点作DH⊥AC于H.连接BH,在点C移动的过程中,BH的最小值是(
)
A.
B.
C.
D.
二、填空题(15分)
11.如图,等边△ABC中,D在BC上,E在AC上,BD=CE,连BE、AD交于F,T在EF上,且DT=CE,AF=50,TE=16,则FT=_____.
12.如图,在⊙O中,是⊙O的直径,,点是点关于的对称点,是上的一动点,下列结论:①;②;③;④的最小值是10.上述结论中正确的个数是_________.
13.如图,在矩形中,是的中点,是边上一动点,将沿着翻折,使得点落在点处,矩形内有一动点连接则的最小值为_______________________.
14.如图,点I为△ABC的内心,连AI交△ABC的外接圆于点D,若,点E为弦AC的中点,连接EI,IC,若,,则IE的长为__.
15.如图,平面直角坐标系中有正方形OABC,B(4,4),动点D从B出发向C运动,动点E从A出发向B运动,且动点D、E运动的速度相同.当它们到达各自终点时停止运动,运动过程中线段OE、AD相交于点H,F是线段OC上任意一点,当BF+FH最小时,点F的坐标为_____.
三、解答题(75分)
16.已知⊙的直径为,点,点,点在⊙上,的平分线交⊙于点.
()如图①,若为⊙的直径,,求,,的长.
()如图②,若,求的长.
17.如图,在⊙O中,AB是直径,P为AB上一点,过点P作弦MN,∠NPB=45°.
(1)若AP=2,BP=6,求MN的长;
(2)若MP=3,NP=5,求AB的长;
(3)当P在AB上运动时(∠NPB=45°不变),的值是否发生变化?若不变,请求出其值;若变化,请求出其范围.
18.如图1,抛物线过点,,点为直线下方抛物线上一动点,为抛物线顶点,抛物线对称轴与直线交于点.
(1)求抛物线的表达式与顶点的坐标;
(2)在直线上是否存在点,使得,,,为顶点的四边形是平行四边形,若存在,请求出点坐标;
(3)在轴上是否存在点,使?若存在,求点的坐标;若不存在,请说明理由.
19.(问题提出)
对于给定三角形,如何求它的外接圆直径呢?
(初步思考)
对于任意三角形,可以分三类进行研究:直角三角形、锐角三角形和钝角三角形.由于直角三角形的斜边就是其外接圆的直径,故我们将研究的重点放在锐角三角形和钝角三角形上.下列研究以钝角三角形作为对象(可用类似方法研究锐角三角形).
(深入研究)
规定△ABC是钝角三角形,∠A是钝角,⊙O是△ABC的外接圆,下面分4种情况求⊙O的直径(结果需用含有各情况中表示线段或角的字母的式子表示).
(1)如图①,AB=m,∠ABC=α,∠ACB=β.
思路:连接AO并延长,交⊙O于点D,连接BD.易得△ABD是直角三角形,AB=m,∠D=∠C=β,此时可求出⊙O的直径AD的长.根据上述思路,直接写出⊙O直径的长.
(2)如图②,BC=m,∠ABC=α,∠ACB=β.
类比(1)的思路,连接CO并延长,交⊙O于点D,连接BD,则⊙O的直径为
.
(3)如图③,BC=m,AB=n,∠ABC=α.根据上述思路,直接写出⊙O直径的长.
(4)如图④,BC=a,AC=b,AB=c.根据上述思路,直接写出⊙O直径的长.
20.已知:如图1,在平面直角坐标系中,A(2,-1),以M(-1,0)为圆心,以AM为半径的圆交y轴于点B,连结BM并延长交⊙M于点C,动点P在线段BC上运动,长为的线段PQ∥x轴(点Q在点P右侧),连结AQ.
(1)求⊙M的半径长和点B的坐标;
(2)如图2,连结AC,交线段PQ于点N,
①求AC所在直线的解析式;
②当PN=QN时,求点Q的坐标;
(3)点P在线段BC上运动的过程中,请直接写出AQ的最小值和最大值.
21.阅读下面材料:
对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A被这个圆所覆盖.
对于平面图形A,如果存在两个或两个以上的圆,使图形A上的任意一点到其中某个圆的圆心的距离都不大于这个圆的半径,则称图形A被这些圆所覆盖.
例如:图1中①的三角形被一个圆覆盖,②中的四边形被两个圆所覆盖.
回答下列问题:
(1)边长为1
cm的正方形被一个半径为r的圆所覆盖,r的最小值是______
cm;
(2)边长为1
cm的等边三角形被一个半径为r的圆所覆盖,r的最小值是_____
cm;
(3)长为2
cm,宽为1
cm的矩形被两个半径均为r的圆所覆盖,r的最小值是_____
cm.这两个圆的圆心距是_____
cm..
22.已知如图,抛物线y=x2+mx+n的顶点为(1,﹣),其图象与x轴交于A,B两点,与y轴交于点C.
(1)m= ,n= ;
(2)点P在抛物线的对称轴上,当∠APC=∠BAC时,求点P的坐标;
(3)点M为线段AC的中点,点N是线段AB上的动点,在△ABC绕点C按逆时针方向旋转的过程中,点N的对应点是点N′,直接写出线段MN′长度的最大值和最小值.
23.如图,AB是⊙O的直径,C,D,E是⊙O上的点,若
,∠E=70°,求∠ABC的度数.
【参考答案】
1.B
2.C
3.D
4.D
5.D
6.A
7.D
8.C
9.B
10.C
11.17
12.3
13.
14.4
15.(0,)
16.(1)AC=8,BD=CD=5;(2)5.
17.(1);(2);(3)不变,值为
18.(1),点的坐标为(1,-4);(2)符合条件的点的坐标为,;(3)点的坐标为或.
19.(1);(2);(3);(4).
20.(1)半径为,点B(0,3);
(2)①yAC=x-2,②点Q坐标为(-,-)
(3)AQ最小值为,AQ最大值为
21.(1)
;(2);(3)
,
1.
22.(1)﹣,﹣2;(2)满足条件的点P的坐标为(1,)或(1,﹣);(3)MN'的最小值为2﹣,最大值为+2.
23.40°
同课章节目录
