人教版数学九年级 上册24.3正多边形的有关概念、正多边形与圆的关系课件(17张)
文档属性
| 名称 | 人教版数学九年级 上册24.3正多边形的有关概念、正多边形与圆的关系课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 472.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-18 14:48:10 | ||
图片预览



文档简介
(共17张PPT)
24.3正多边形和圆
学习目标
1.了解正多边形和圆的有关概念.
2.理解并掌握正多边形半径、边长、边心距、中心角之间的关系,会应用正多边形和圆的有关知识画正多边形.
练习1
矩形是正多边形吗?菱形呢?正方形吗?为什么?
答:
.
思考
各边相等的多边形是正多边形吗?为什么?答:
.
各角相等的多边形呢?你能举反例吗?
答:
.
温故知新
1.正多边形的定义:
的多边形是正多边形.
不一定,因为各角不一定都相等
不一定,反例:矩形
矩形不是正多边形,菱形也不是,正方形是正多边形;
矩形只满足各角相等,菱形只满足各边相等
各边都相等,各角也都相等
温故知新
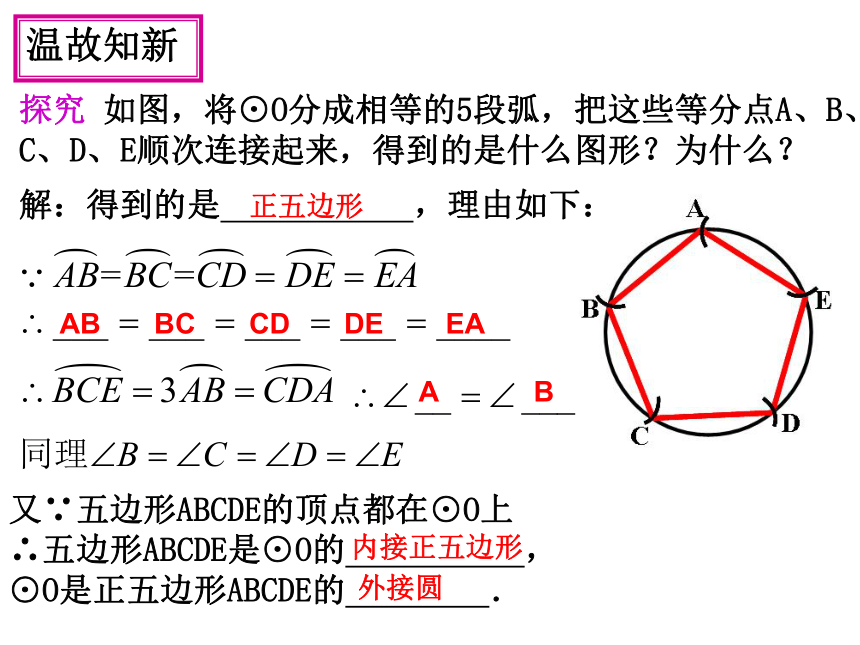
探究
如图,将⊙O分成相等的5段弧,把这些等分点A、B、C、D、E顺次连接起来,得到的是什么图形?为什么?
解:得到的是
,理由如下:
又∵五边形ABCDE的顶点都在⊙O上
∴五边形ABCDE是⊙O的
,
⊙O是正五边形ABCDE的
.
正五边形
AB
BC
CD
DE
EA
A
B
内接正五边形
外接圆
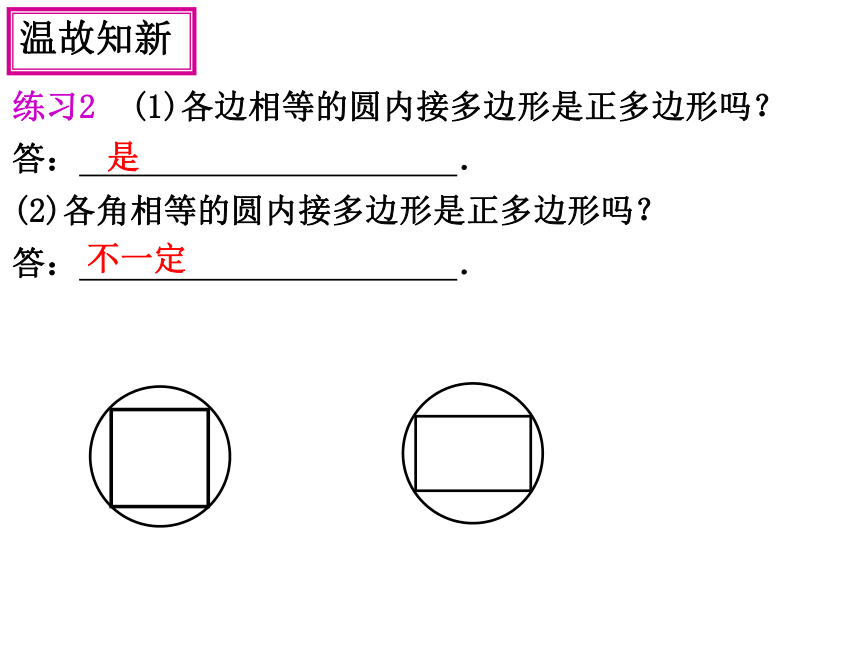
练习2
(1)各边相等的圆内接多边形是正多边形吗?
答:
.
(2)各角相等的圆内接多边形是正多边形吗?
答:
.
温故知新
是
不一定
探索新知
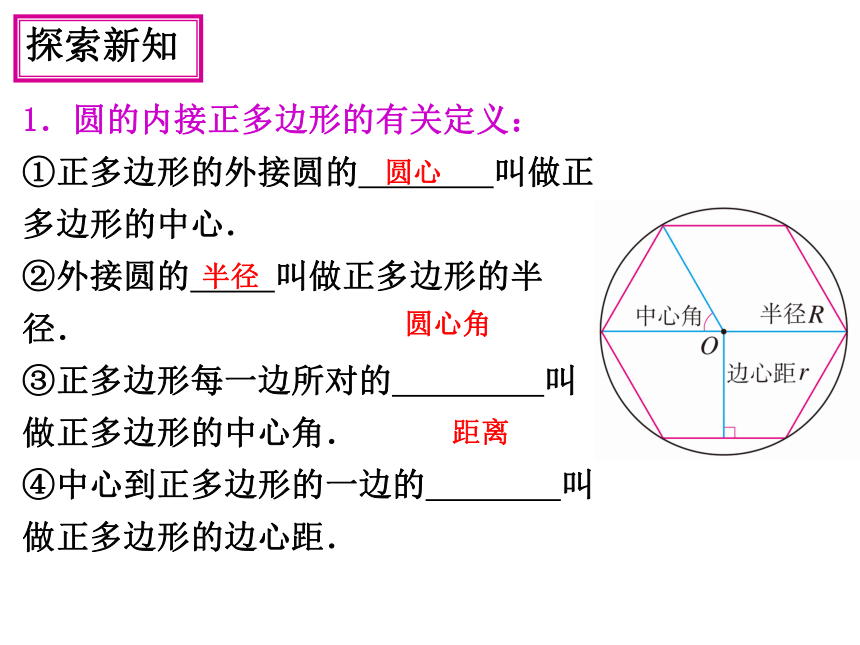
1.圆的内接正多边形的有关定义:
①正多边形的外接圆的
叫做正多边形的中心.
②外接圆的
叫做正多边形的半径.
③正多边形每一边所对的
叫做正多边形的中心角.
④中心到正多边形的一边的
叫做正多边形的边心距.
圆心
半径
圆心角
距离
探索新知
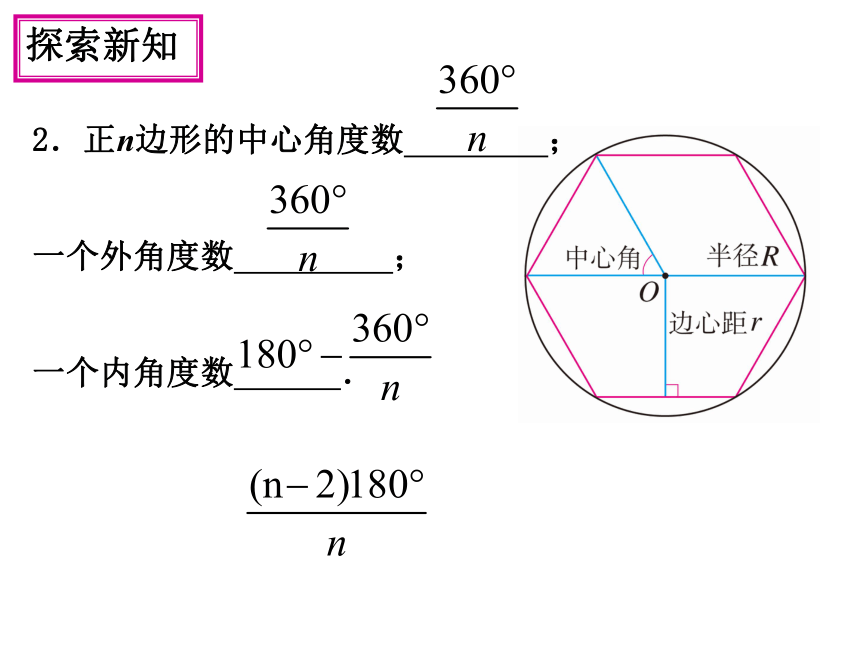
2.正n边形的中心角度数
;
一个外角度数
;
一个内角度数
.
探索新知
例
有一个亭子(如图),它的地基是半径为4m的正六边形,求地基的周长和面.
正多边形
边数
内角
中心角
半径
边长
边心距
周长
面积
3
60°
4
1
6
练习3
下图分别画出半径为R的圆内接正三角形、正方形、正六边形,借助各图完成下表.
正多边形
边数
内角
中心角
半径
边长
边心距
周长
面积
3
60°
4
1
6
再探新知
分别画出⊙O的圆内接正三角形、正方形、正六边形.
课堂小结
1.各边相等、各角也相等的多边形是正多边形.
2.圆内接正多边形的有关定义.
课后作业
1.如图,正六边形ABCDEF内接于⊙O,则∠ADB的度数是(
)
A.60°
B.45°
C.30°
D.22.5°
2.圆内接正五边形ABCDE中,对角线AC和BD相交于点P,则∠APB的度数是(
)
A.36°
B.60°
C.72°
D.108°
C
C
课后作业
3.如图,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时
∠AOE=56°,则α的度数是(
)
A.52°
B.60°
C.72°
D.76°
A
课后作业
4.正
n
边形的一个外角为
30°,则它的边数为____,它的内角和为______.
5.正
n
边形的一个内角为120°,则它的边数为____,它的内角和为______.
6.若一个正多边形的每个内角的度数是中心角的3倍,则这个正多边形的边数是
.
7.正三角形的半径为
R,则边长为_____,边心距为______,面积为________.
12
1800°
6
720°
8
R
课后作业
8.正三角形的高∶半径∶边心距为_________;
9.半径为R的圆内接正方形的边长为
,边心距为
,面积为
.
10.边长为a的正六边形的边心距是_________,周长是_________,面积是______.
11.要用圆形铁片截出边长为a的正方形铁片,选用的圆形铁片的半径至少是
.
课后作业
12.如图所示,正五边形ABCDE的对角线AC、BE相交于M.求证:四边形CDEM是菱形.
1
2
24.3正多边形和圆
学习目标
1.了解正多边形和圆的有关概念.
2.理解并掌握正多边形半径、边长、边心距、中心角之间的关系,会应用正多边形和圆的有关知识画正多边形.
练习1
矩形是正多边形吗?菱形呢?正方形吗?为什么?
答:
.
思考
各边相等的多边形是正多边形吗?为什么?答:
.
各角相等的多边形呢?你能举反例吗?
答:
.
温故知新
1.正多边形的定义:
的多边形是正多边形.
不一定,因为各角不一定都相等
不一定,反例:矩形
矩形不是正多边形,菱形也不是,正方形是正多边形;
矩形只满足各角相等,菱形只满足各边相等
各边都相等,各角也都相等
温故知新
探究
如图,将⊙O分成相等的5段弧,把这些等分点A、B、C、D、E顺次连接起来,得到的是什么图形?为什么?
解:得到的是
,理由如下:
又∵五边形ABCDE的顶点都在⊙O上
∴五边形ABCDE是⊙O的
,
⊙O是正五边形ABCDE的
.
正五边形
AB
BC
CD
DE
EA
A
B
内接正五边形
外接圆
练习2
(1)各边相等的圆内接多边形是正多边形吗?
答:
.
(2)各角相等的圆内接多边形是正多边形吗?
答:
.
温故知新
是
不一定
探索新知
1.圆的内接正多边形的有关定义:
①正多边形的外接圆的
叫做正多边形的中心.
②外接圆的
叫做正多边形的半径.
③正多边形每一边所对的
叫做正多边形的中心角.
④中心到正多边形的一边的
叫做正多边形的边心距.
圆心
半径
圆心角
距离
探索新知
2.正n边形的中心角度数
;
一个外角度数
;
一个内角度数
.
探索新知
例
有一个亭子(如图),它的地基是半径为4m的正六边形,求地基的周长和面.
正多边形
边数
内角
中心角
半径
边长
边心距
周长
面积
3
60°
4
1
6
练习3
下图分别画出半径为R的圆内接正三角形、正方形、正六边形,借助各图完成下表.
正多边形
边数
内角
中心角
半径
边长
边心距
周长
面积
3
60°
4
1
6
再探新知
分别画出⊙O的圆内接正三角形、正方形、正六边形.
课堂小结
1.各边相等、各角也相等的多边形是正多边形.
2.圆内接正多边形的有关定义.
课后作业
1.如图,正六边形ABCDEF内接于⊙O,则∠ADB的度数是(
)
A.60°
B.45°
C.30°
D.22.5°
2.圆内接正五边形ABCDE中,对角线AC和BD相交于点P,则∠APB的度数是(
)
A.36°
B.60°
C.72°
D.108°
C
C
课后作业
3.如图,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时
∠AOE=56°,则α的度数是(
)
A.52°
B.60°
C.72°
D.76°
A
课后作业
4.正
n
边形的一个外角为
30°,则它的边数为____,它的内角和为______.
5.正
n
边形的一个内角为120°,则它的边数为____,它的内角和为______.
6.若一个正多边形的每个内角的度数是中心角的3倍,则这个正多边形的边数是
.
7.正三角形的半径为
R,则边长为_____,边心距为______,面积为________.
12
1800°
6
720°
8
R
课后作业
8.正三角形的高∶半径∶边心距为_________;
9.半径为R的圆内接正方形的边长为
,边心距为
,面积为
.
10.边长为a的正六边形的边心距是_________,周长是_________,面积是______.
11.要用圆形铁片截出边长为a的正方形铁片,选用的圆形铁片的半径至少是
.
课后作业
12.如图所示,正五边形ABCDE的对角线AC、BE相交于M.求证:四边形CDEM是菱形.
1
2
同课章节目录
