人教版数学九年级上册24.2.1反证法课件(19张)
文档属性
| 名称 | 人教版数学九年级上册24.2.1反证法课件(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 315.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-18 14:48:57 | ||
图片预览





文档简介
(共19张PPT)
小故事:
中国古代有一个叫《路边苦李》的故事:王戎7岁时,与小伙伴们外出游玩,看到路边的李树上结满了果子.小伙伴们纷纷去摘取果子,只有王戎站在原地不动.有人问王戎为什么?
王戎回答说:“树在道边而多子,此必苦李.”
小伙伴摘取一个尝了一下,果然是苦李.
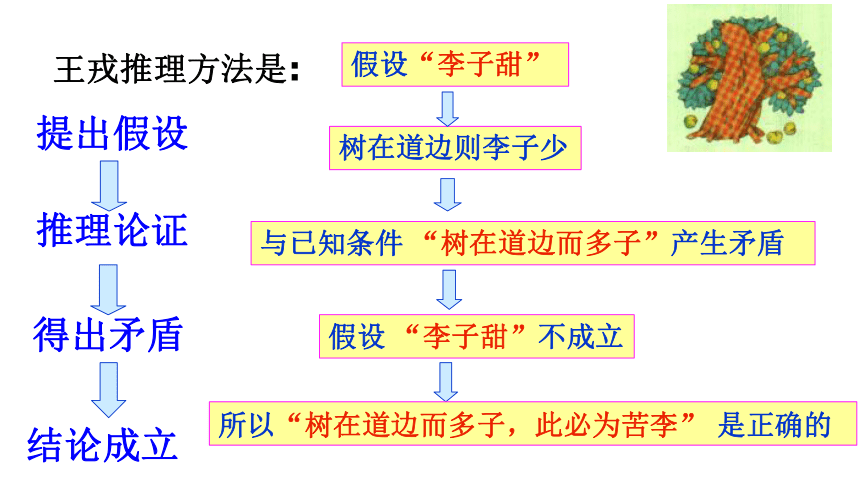
王戎是怎样知道李子是苦的呢?他运用了怎样的推理方法?你想知道吗?
假设“李子甜”
树在道边则李子少
与已知条件
“树在道边而多子”产生矛盾
假设
“李子甜”不成立
所以“树在道边而多子,此必为苦李”
是正确的
王戎推理方法是:
提出假设
推理论证
得出矛盾
结论成立
反证法定义:
在证明一个命题时,人们有时
先假设命题不成立,
从这样的假设出发,经过推理得出和已知条件或者与定义、公理、定理等相矛盾.
从而得出假设命题不成立,是错误的,
即所求证的命题正确.
这种证明方法叫做反证法.
24.2.1
反证法
a<0
b是0或负数
a不垂直于b
a∥b
1.写出下列各结论的反面:
(1)a//b
(2)a≥0
(3)b是正数
(4)a⊥b
试
一
试
新课标教学网(www.xkbw.com)--海量教学资源欢迎下载!
2.“a<b”的反面应是(
)
(A)a≠>b
(B)a
>b
(C)a=b
(D)a=b或a
>b
3.用反证法证明命题“三角形中最多有一个角是直角”时,应如何假设?
___________________________________
D
假设三角形中有两个或三个角是直角
举一反三
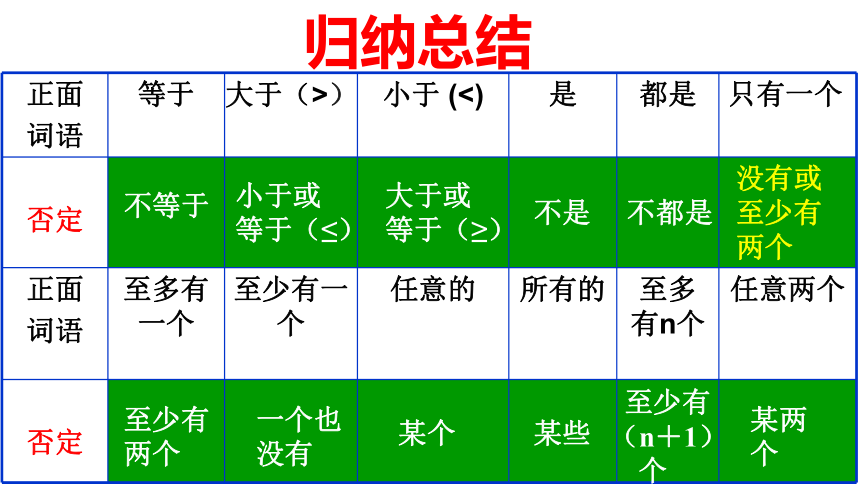
正面
词语
等于
大于(>)
小于
(<)
是
都是
只有一个
否定
正面
词语
至多有一个
至少有一个
任意的
所有的
至多有n个
任意两个
否定
不等于
小于或
等于(≤)
大于或
等于(≥)
不是
不都是
至少有两个
一个也没有
某个
某些
至少有
(n+1)
个
某两个
归纳总结
没有或
至少有
两个
用反证法证明(填空):在三角形的内角中,至少有一个角大于或等于60°.
已知:
∠A,∠B,∠C是△ABC的内角.
求证:
∠A,∠B,∠C中至少有一个角大
于或等于60°.
例1--几何类
这与________________________________相矛盾.
所以______不成立.
证明:
假设∠A,∠B,∠C
中三个角都小于
60°,
即
∠A
___
60°
,∠B
___
60°
,∠C
___60°
则∠A+∠B+∠C
<
180°.
<
<
<
三角形三个内角的和等于180°
假设
所以
∠A,∠B,∠C中至少有一个角大于或等于60°.
求证:如果a>b>0,那么
例2--代数类
明
:
反证法的步骤
一、提出假设
二、推理论证
三、得出矛盾
四、结论成立
假设命题不成立(即命题的反面成立)
从假设出发经过推理
与已知条件或定义、基本事实、定理、公理矛盾
从而说明假设不成立,原命题成立
已知:如图,直线a,b被直线c所截,
∠1
≠
∠2
求证:a∥b
∴∠1=∠2
(两直线平行,同位角相等)
这与已知的∠1≠∠2矛盾
∴假设不成立
证明:假设结论不成立,则a∥b
练一练1
∴a∥b
求证:四边形中至少有一个角是钝角或直角.
已知:如图,
四边形ABCD.
求证:
四边形ABCD中至少有一个角是钝角或直角.
证明:
A
B
C
D
假设四边形ABCD中没有一个角是钝角或直角,
即∠A_90°,
∠B_90°,∠C_90°,∠D
_90°
则∠A+∠B+∠C+∠D<360度
这于
__________
矛盾
所以假设命题______.
所以,四边形ABCD中至少有一个角是钝角或直角.
<
<
<
四边形的内角和等于360°
不成立
<
练一练2
已知:如图,在⊙O中,弦AB、CD交于点P,且AB、CD不是直径.求证:弦AB、CD不被P平分.
P
O
B
A
D
C
由于P点一定不是圆心O,连结OP,根据垂径定理的推论,有
所以,弦AB、CD不被P平分。
证明:
假设弦AB、CD被P平分,
即过点P有两条直线与OP都垂直,
这与垂线性质矛盾,即假设不成立
OP⊥AB,OP⊥CD,
练一练3
应用反证法的情形:
(1)直接证明困难;
(2)需分成很多类进行讨论;
(3)结论为“至少”、“至多”、“有无穷多个”类命题;
(4)结论为
“唯一”类命题.
课堂总结
警察局里有5名嫌疑犯,他们分别做了如下口供:
A说:这里有1个人说谎.
B说:这里有2个人说谎.
C说:这里有3个人说谎.
D说:这里有4个人说谎.
E说:这里有5个人说谎.
聪明的同学们,假如你是警察,你觉得谁说了真话?
你会释放谁?
请与大家分享你的判断!
我来当警察:
结束寄语
伟大人格的素质,重要的是一个“诚”字。
----鲁迅
新课标教学网(www.xkbw.com)--海量教学资源欢迎下载!
布置作业:
1.必做:习题中相关题目
2.选做:用反证法解决生活中的问题。
下课了!
再
见
谢谢!
小故事:
中国古代有一个叫《路边苦李》的故事:王戎7岁时,与小伙伴们外出游玩,看到路边的李树上结满了果子.小伙伴们纷纷去摘取果子,只有王戎站在原地不动.有人问王戎为什么?
王戎回答说:“树在道边而多子,此必苦李.”
小伙伴摘取一个尝了一下,果然是苦李.
王戎是怎样知道李子是苦的呢?他运用了怎样的推理方法?你想知道吗?
假设“李子甜”
树在道边则李子少
与已知条件
“树在道边而多子”产生矛盾
假设
“李子甜”不成立
所以“树在道边而多子,此必为苦李”
是正确的
王戎推理方法是:
提出假设
推理论证
得出矛盾
结论成立
反证法定义:
在证明一个命题时,人们有时
先假设命题不成立,
从这样的假设出发,经过推理得出和已知条件或者与定义、公理、定理等相矛盾.
从而得出假设命题不成立,是错误的,
即所求证的命题正确.
这种证明方法叫做反证法.
24.2.1
反证法
a<0
b是0或负数
a不垂直于b
a∥b
1.写出下列各结论的反面:
(1)a//b
(2)a≥0
(3)b是正数
(4)a⊥b
试
一
试
新课标教学网(www.xkbw.com)--海量教学资源欢迎下载!
2.“a<b”的反面应是(
)
(A)a≠>b
(B)a
>b
(C)a=b
(D)a=b或a
>b
3.用反证法证明命题“三角形中最多有一个角是直角”时,应如何假设?
___________________________________
D
假设三角形中有两个或三个角是直角
举一反三
正面
词语
等于
大于(>)
小于
(<)
是
都是
只有一个
否定
正面
词语
至多有一个
至少有一个
任意的
所有的
至多有n个
任意两个
否定
不等于
小于或
等于(≤)
大于或
等于(≥)
不是
不都是
至少有两个
一个也没有
某个
某些
至少有
(n+1)
个
某两个
归纳总结
没有或
至少有
两个
用反证法证明(填空):在三角形的内角中,至少有一个角大于或等于60°.
已知:
∠A,∠B,∠C是△ABC的内角.
求证:
∠A,∠B,∠C中至少有一个角大
于或等于60°.
例1--几何类
这与________________________________相矛盾.
所以______不成立.
证明:
假设∠A,∠B,∠C
中三个角都小于
60°,
即
∠A
___
60°
,∠B
___
60°
,∠C
___60°
则∠A+∠B+∠C
<
180°.
<
<
<
三角形三个内角的和等于180°
假设
所以
∠A,∠B,∠C中至少有一个角大于或等于60°.
求证:如果a>b>0,那么
例2--代数类
明
:
反证法的步骤
一、提出假设
二、推理论证
三、得出矛盾
四、结论成立
假设命题不成立(即命题的反面成立)
从假设出发经过推理
与已知条件或定义、基本事实、定理、公理矛盾
从而说明假设不成立,原命题成立
已知:如图,直线a,b被直线c所截,
∠1
≠
∠2
求证:a∥b
∴∠1=∠2
(两直线平行,同位角相等)
这与已知的∠1≠∠2矛盾
∴假设不成立
证明:假设结论不成立,则a∥b
练一练1
∴a∥b
求证:四边形中至少有一个角是钝角或直角.
已知:如图,
四边形ABCD.
求证:
四边形ABCD中至少有一个角是钝角或直角.
证明:
A
B
C
D
假设四边形ABCD中没有一个角是钝角或直角,
即∠A_90°,
∠B_90°,∠C_90°,∠D
_90°
则∠A+∠B+∠C+∠D<360度
这于
__________
矛盾
所以假设命题______.
所以,四边形ABCD中至少有一个角是钝角或直角.
<
<
<
四边形的内角和等于360°
不成立
<
练一练2
已知:如图,在⊙O中,弦AB、CD交于点P,且AB、CD不是直径.求证:弦AB、CD不被P平分.
P
O
B
A
D
C
由于P点一定不是圆心O,连结OP,根据垂径定理的推论,有
所以,弦AB、CD不被P平分。
证明:
假设弦AB、CD被P平分,
即过点P有两条直线与OP都垂直,
这与垂线性质矛盾,即假设不成立
OP⊥AB,OP⊥CD,
练一练3
应用反证法的情形:
(1)直接证明困难;
(2)需分成很多类进行讨论;
(3)结论为“至少”、“至多”、“有无穷多个”类命题;
(4)结论为
“唯一”类命题.
课堂总结
警察局里有5名嫌疑犯,他们分别做了如下口供:
A说:这里有1个人说谎.
B说:这里有2个人说谎.
C说:这里有3个人说谎.
D说:这里有4个人说谎.
E说:这里有5个人说谎.
聪明的同学们,假如你是警察,你觉得谁说了真话?
你会释放谁?
请与大家分享你的判断!
我来当警察:
结束寄语
伟大人格的素质,重要的是一个“诚”字。
----鲁迅
新课标教学网(www.xkbw.com)--海量教学资源欢迎下载!
布置作业:
1.必做:习题中相关题目
2.选做:用反证法解决生活中的问题。
下课了!
再
见
谢谢!
同课章节目录
