苏科版九年级数学下册知识点《锐角三角函数》及习题(word版,含解析)
文档属性
| 名称 | 苏科版九年级数学下册知识点《锐角三角函数》及习题(word版,含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 893.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-16 20:33:45 | ||
图片预览


文档简介
2020—2021学年初三数学第一学期知识点
《锐角三角函数》知识点总结
锐角三角函数是初中数学的重要内容,是中考命题的热点之一课程标准中对锐角三角函数的学习要求有以下几点:(1)利用相似的直角三角形,探索并认识锐角三角函数(,,
),知道30?、45?、60?角的三角函数值;(2)会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它的对应锐角;(3)能用锐角三角函数解直角三角形,能用相关知识解决一些简单的实际问题.
一、自主探究
1.如右图,在Rt△ABC中,∠C为直角,则∠A的锐角三角函数为(∠A可换成∠B):
2.30°、45°、60°特殊角的三角函数值:
30°
45°
60°
sinA
cosA
tanA
锐角三角函数值的性质,锐角三角函数的大小比较:
在时,随着角的增大,正切值和正弦值越来越大,而余弦值越来越小.
即:tanA
和是增函数,减函数。
3、解直角三角形方法:Rt△ABC(∠C=90°)的边、角之间有哪些关系:
(1)边角之间关系:
如果用表示直角三角形的一个锐角,那上述式子就可以写成.
(2)三边之间关系
?(3)锐角之间关系∠A+∠B=90°.
?a2
+b2
=c2
(勾股定理)
?以上三点正是解直角三角形的依据.
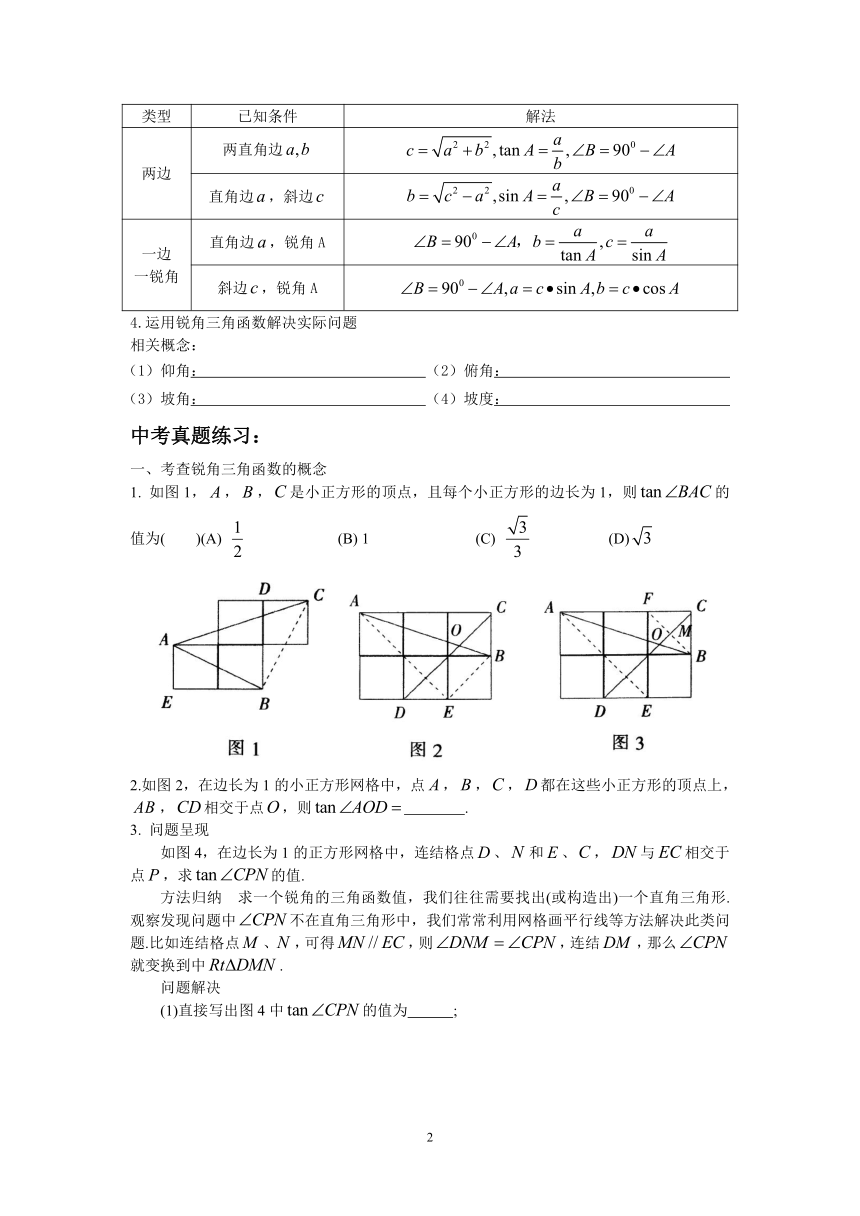
(3)解直角三角形基本类型及解法总结:
类型
已知条件
解法
两边
两直角边
直角边,斜边
一边一锐角
直角边,锐角A
斜边,锐角A
4.运用锐角三角函数解决实际问题
相关概念:
(1)仰角:
(2)俯角:
(3)坡角:
(4)坡度:
中考真题练习:
一、考查锐角三角函数的概念
1.
如图1,,,是小正方形的顶点,且每个小正方形的边长为1,则的值为(
)(A)
(B)
1
(C)
(D)
2.如图2,在边长为1的小正方形网格中,点,,,都在这些小正方形的顶点上,,相交于点,则
.
3.
问题呈现
如图4,在边长为1的正方形网格中,连结格点、和、,与相交于点,求的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连结格点、,可得,则,连结,那么就变换到中.
问题解决
(1)直接写出图4中的值为
;
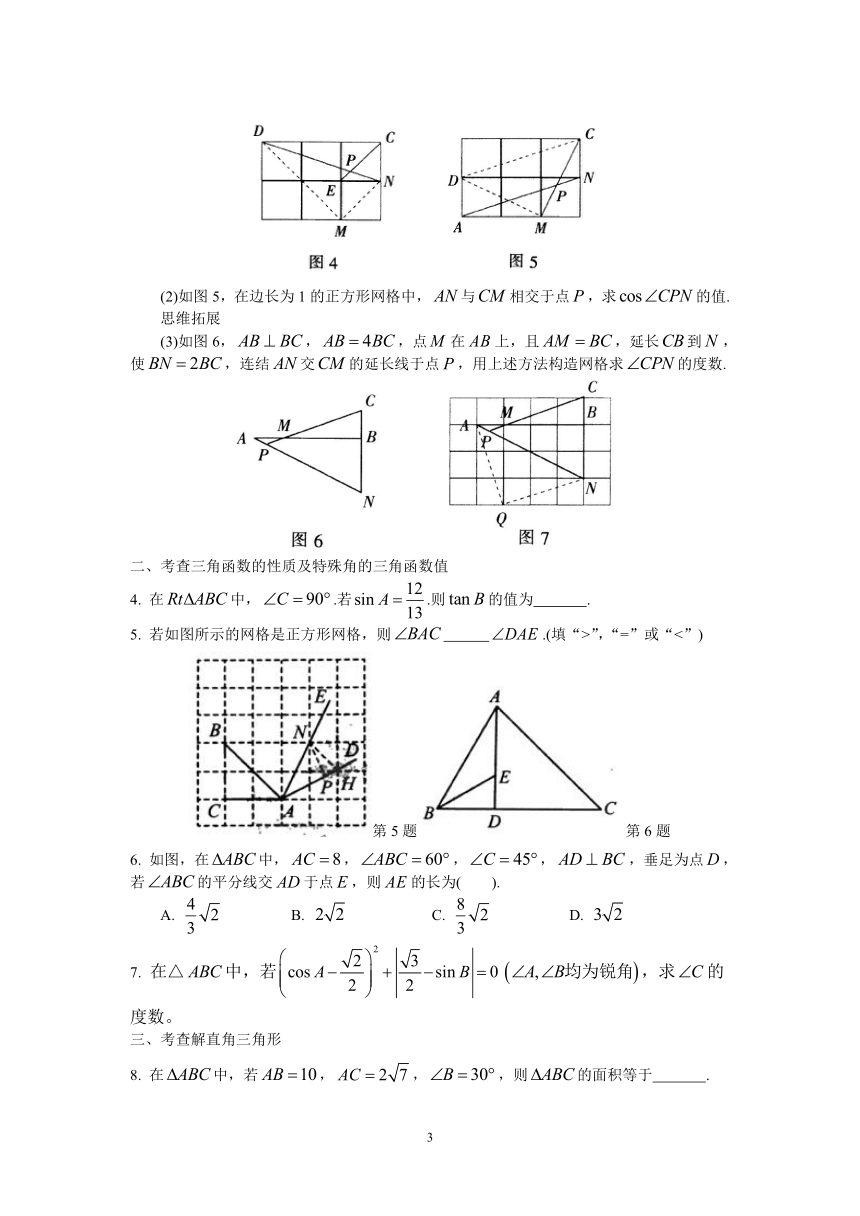
(2)如图5,在边长为1的正方形网格中,与相交于点,求的值.
思维拓展
(3)如图6,,,点在上,且,延长到,使,连结交的延长线于点,用上述方法构造网格求的度数.
二、考查三角函数的性质及特殊角的三角函数值
4.
在中,.若.则的值为
.
5.
若如图所示的网格是正方形网格,则
.(填“>”,“=”或“<”)
第5题第6题
6.
如图,在中,,,,,垂足为点,若的平分线交于点,则的长为(
).
A.
B.
C.
D.
7.
在△中,若,求的度数。
三、考查解直角三角形
8.
在中,若,,,则的面积等于
.
9.
如图,在四边形中,是对角线,,若,,,,则线段
.
四、考查用解直角三角触的知识解决实际问题
10.
数学实践活动小组借助载有测角仪的无人机测量象山岚光阁与文明湖湖心亭之间的距离.如图15,无人机所在位置与岚光阁阁顶、湖心亭在同一铅垂面内,点与点的垂直距离为300米,点与点的垂直距离为150米,在点处测得,两点的俯角分另。为,,且,,试求岚光阁与湖心亭之间的距离.(计算结果若含有根号,请保留根号)
参考答案
1.解法1
连结,根据网格的特征,借助勾股定理,可得
,,即,∴.
在中,.故选B.
解法2连结,根据网格的特征,可知:,
∴,,∴
.在中,.故选B.
反思探究我们知道锐角三角函数值是在直角三角形中定义的,因此探究的值,必须将放到某个直角三角形中.观察图1的结构我们发现,连结即可得到一个所需的直角三角形.至于如何判断为直角三角形,解法1是通过计算三角形的边长,利用勾股定理的逆定理来确认的;解法2则是通过三角形的全等和网格直角的特性通过角之间的等量代换得到的.
由此可见,仔细观察所求锐角在网格中的位置特征,慧眼识图发现所求的锐角所在直角三角形(或者通过添加辅助线构造出所需的直角三角形),是解决此类问题的关键.
2.
解法1如图2,连结,.观察网格中线段,与分别是以2,1为边长的3个正方形的对角线.显然,,故有,.
根据勾股定理,得,.在中,有
解法2
如图3,连结交于点,则于(),由对顶角相等可知。在中,有
观察图3,发现,∴,即.
而,∴.又,
∴.在中,.
评注
解法1是通过构造的平行线,利用两直线平行,同位角相等,把所求的锐角转化为较为容易判断的中的锐角,然后利用锐角三角函数的定义解决问题.
解法2是利用了正方形的对角线互相垂直的性质,构造了一个直角,并借助对顶角相等,把所求的锐角三角函数的锐角转化为这个直角三角形的一个锐角,然后利用其定义转化为两条直角边的比值.在探究两直角边的长度时,又巧妙的运用了相似三角形对应边成比例的性质,以及正方形的有关性质.
3.
解(1)如图4,连结,.
∵,∴,∴.
∵,∴.
(2)如图5中,取格点,连接,.∵,∴.
∵是等腰直角三角形,∴,
∴.
(3)如图7中,取格点,连接、.∵,∴,
∵,,∴,∴.
评注
(2)小题也可以过点构造的平行线,连接,将转化到等腰直角中来探究.(3)小题实际上是要求读者根据问题的条件设置网格背景,从而在网格的情境下,迁移(1)(2)的方法解决问题.本题综合考查了平行线的性质、勾股定理、直角三角形(等腰直角三角形)的判定和性质等知识,渗透了数形结合思想、转化等数学思想.
4.
∵,,∴
(负值舍去).
∵在中,,∴,,
∴.故填.
5.
解析:设小正方形的边长为1。如图5,连接,,过点作,垂足为点.∵,,∴.
在中,.
在中,.
∵,且正弦值随着角度的增大而增大,
∴
>.
故填>.
6.
解析:∵平分,,∴.
∵,∴.
在中,.
∵,∴,∴,
∴.在中,.
∴.故选C.
7.
解
由题意得解得又∵均为锐角,∴,。∴.
说明
解这类问题首先要熟记特殊角的三角函数值,还要掌握一些化简的技巧。
8.
解析:有两种情况:
(1)当高在内部时,如图9.
在中,∵,,∴,.
在中,∵,∴.∴.
∴.
(2)当高在外部时,如图10.
由(1)可知,,,则.
∴.综上,的面积为或。故填或.
9.
解析:如图,作,,垂足分别为点,.
在中,∵∴设,则.由勾股定理,得,即.解得.∴,.
在中,∵,∴.
∵,,
∴.∴.
设,则,.又,∴,.
∴,∴.故填17.
10.
解析:如图,过点作、垂足为点,过点作,垂足为点,则由题意可得,,,.
在中,.
∵,∴四边形是矩形.
∴,,∴.
在中,,
∴.在中,。
答:岚光阁与湖心亭之间的距离为450米.
1
《锐角三角函数》知识点总结
锐角三角函数是初中数学的重要内容,是中考命题的热点之一课程标准中对锐角三角函数的学习要求有以下几点:(1)利用相似的直角三角形,探索并认识锐角三角函数(,,
),知道30?、45?、60?角的三角函数值;(2)会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它的对应锐角;(3)能用锐角三角函数解直角三角形,能用相关知识解决一些简单的实际问题.
一、自主探究
1.如右图,在Rt△ABC中,∠C为直角,则∠A的锐角三角函数为(∠A可换成∠B):
2.30°、45°、60°特殊角的三角函数值:
30°
45°
60°
sinA
cosA
tanA
锐角三角函数值的性质,锐角三角函数的大小比较:
在时,随着角的增大,正切值和正弦值越来越大,而余弦值越来越小.
即:tanA
和是增函数,减函数。
3、解直角三角形方法:Rt△ABC(∠C=90°)的边、角之间有哪些关系:
(1)边角之间关系:
如果用表示直角三角形的一个锐角,那上述式子就可以写成.
(2)三边之间关系
?(3)锐角之间关系∠A+∠B=90°.
?a2
+b2
=c2
(勾股定理)
?以上三点正是解直角三角形的依据.
(3)解直角三角形基本类型及解法总结:
类型
已知条件
解法
两边
两直角边
直角边,斜边
一边一锐角
直角边,锐角A
斜边,锐角A
4.运用锐角三角函数解决实际问题
相关概念:
(1)仰角:
(2)俯角:
(3)坡角:
(4)坡度:
中考真题练习:
一、考查锐角三角函数的概念
1.
如图1,,,是小正方形的顶点,且每个小正方形的边长为1,则的值为(
)(A)
(B)
1
(C)
(D)
2.如图2,在边长为1的小正方形网格中,点,,,都在这些小正方形的顶点上,,相交于点,则
.
3.
问题呈现
如图4,在边长为1的正方形网格中,连结格点、和、,与相交于点,求的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连结格点、,可得,则,连结,那么就变换到中.
问题解决
(1)直接写出图4中的值为
;
(2)如图5,在边长为1的正方形网格中,与相交于点,求的值.
思维拓展
(3)如图6,,,点在上,且,延长到,使,连结交的延长线于点,用上述方法构造网格求的度数.
二、考查三角函数的性质及特殊角的三角函数值
4.
在中,.若.则的值为
.
5.
若如图所示的网格是正方形网格,则
.(填“>”,“=”或“<”)
第5题第6题
6.
如图,在中,,,,,垂足为点,若的平分线交于点,则的长为(
).
A.
B.
C.
D.
7.
在△中,若,求的度数。
三、考查解直角三角形
8.
在中,若,,,则的面积等于
.
9.
如图,在四边形中,是对角线,,若,,,,则线段
.
四、考查用解直角三角触的知识解决实际问题
10.
数学实践活动小组借助载有测角仪的无人机测量象山岚光阁与文明湖湖心亭之间的距离.如图15,无人机所在位置与岚光阁阁顶、湖心亭在同一铅垂面内,点与点的垂直距离为300米,点与点的垂直距离为150米,在点处测得,两点的俯角分另。为,,且,,试求岚光阁与湖心亭之间的距离.(计算结果若含有根号,请保留根号)
参考答案
1.解法1
连结,根据网格的特征,借助勾股定理,可得
,,即,∴.
在中,.故选B.
解法2连结,根据网格的特征,可知:,
∴,,∴
.在中,.故选B.
反思探究我们知道锐角三角函数值是在直角三角形中定义的,因此探究的值,必须将放到某个直角三角形中.观察图1的结构我们发现,连结即可得到一个所需的直角三角形.至于如何判断为直角三角形,解法1是通过计算三角形的边长,利用勾股定理的逆定理来确认的;解法2则是通过三角形的全等和网格直角的特性通过角之间的等量代换得到的.
由此可见,仔细观察所求锐角在网格中的位置特征,慧眼识图发现所求的锐角所在直角三角形(或者通过添加辅助线构造出所需的直角三角形),是解决此类问题的关键.
2.
解法1如图2,连结,.观察网格中线段,与分别是以2,1为边长的3个正方形的对角线.显然,,故有,.
根据勾股定理,得,.在中,有
解法2
如图3,连结交于点,则于(),由对顶角相等可知。在中,有
观察图3,发现,∴,即.
而,∴.又,
∴.在中,.
评注
解法1是通过构造的平行线,利用两直线平行,同位角相等,把所求的锐角转化为较为容易判断的中的锐角,然后利用锐角三角函数的定义解决问题.
解法2是利用了正方形的对角线互相垂直的性质,构造了一个直角,并借助对顶角相等,把所求的锐角三角函数的锐角转化为这个直角三角形的一个锐角,然后利用其定义转化为两条直角边的比值.在探究两直角边的长度时,又巧妙的运用了相似三角形对应边成比例的性质,以及正方形的有关性质.
3.
解(1)如图4,连结,.
∵,∴,∴.
∵,∴.
(2)如图5中,取格点,连接,.∵,∴.
∵是等腰直角三角形,∴,
∴.
(3)如图7中,取格点,连接、.∵,∴,
∵,,∴,∴.
评注
(2)小题也可以过点构造的平行线,连接,将转化到等腰直角中来探究.(3)小题实际上是要求读者根据问题的条件设置网格背景,从而在网格的情境下,迁移(1)(2)的方法解决问题.本题综合考查了平行线的性质、勾股定理、直角三角形(等腰直角三角形)的判定和性质等知识,渗透了数形结合思想、转化等数学思想.
4.
∵,,∴
(负值舍去).
∵在中,,∴,,
∴.故填.
5.
解析:设小正方形的边长为1。如图5,连接,,过点作,垂足为点.∵,,∴.
在中,.
在中,.
∵,且正弦值随着角度的增大而增大,
∴
>.
故填>.
6.
解析:∵平分,,∴.
∵,∴.
在中,.
∵,∴,∴,
∴.在中,.
∴.故选C.
7.
解
由题意得解得又∵均为锐角,∴,。∴.
说明
解这类问题首先要熟记特殊角的三角函数值,还要掌握一些化简的技巧。
8.
解析:有两种情况:
(1)当高在内部时,如图9.
在中,∵,,∴,.
在中,∵,∴.∴.
∴.
(2)当高在外部时,如图10.
由(1)可知,,,则.
∴.综上,的面积为或。故填或.
9.
解析:如图,作,,垂足分别为点,.
在中,∵∴设,则.由勾股定理,得,即.解得.∴,.
在中,∵,∴.
∵,,
∴.∴.
设,则,.又,∴,.
∴,∴.故填17.
10.
解析:如图,过点作、垂足为点,过点作,垂足为点,则由题意可得,,,.
在中,.
∵,∴四边形是矩形.
∴,,∴.
在中,,
∴.在中,。
答:岚光阁与湖心亭之间的距离为450米.
1
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
