苏科版七年级数学上册 第4章 一元一次方程培优训练专题(Word版 无答案)
文档属性
| 名称 | 苏科版七年级数学上册 第4章 一元一次方程培优训练专题(Word版 无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 170.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-15 23:07:09 | ||
图片预览


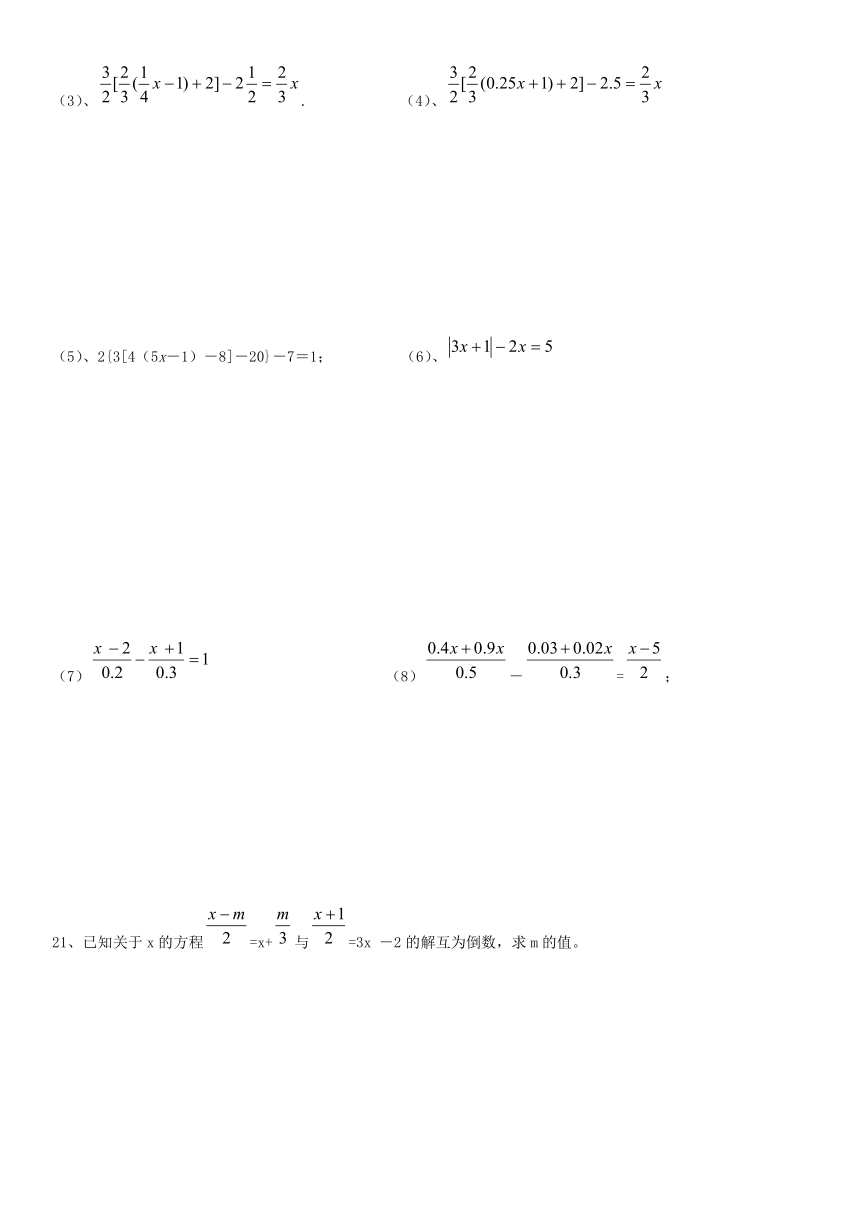

文档简介
一元一次方程培优训练专题
1、若x=1是关于x的方程mx+n=p-1的解,则(m+n-p)2021=______.
2、已知方程的解与关于的方程的解相等,则代数式a?+2a+2020的
值为
3、关于的方程的解比关于y的方程的解小2,则a的值为
4、如表所示,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2021个格子中的数为
5、如果不论是何值,总是关于的方程3(Rx+a)-2(2x-bR)=6的解,则
,
.
已知关于x的一元一次方程的解为,
那么关于y的一元一次方程的解为
.
7、已知方程,则代数式的值为
。
8、在公式中,已知,,=21,则=________.
9、当为整数
时,方程的解为正整数。
李强在解方程□
时,把“□”中的数字看错了,解得
,那么李强把“□”中的数字
看成了
.
11、对于有理数、,规定,若,则的值为
.
12、小明今年13岁,妈妈38岁,
年后,小明年龄是妈妈的.
13、某学生读一本书,第一天读全书的还多6页,第二天再读剩下的,还有100页没有读,则全书有
页
14、北京奥运会的金牌是用金、银和玉三种物质混合而建的,它的总重量为244.5克,如果金、银、玉的重量之比为7:9:6,则金牌中的的重量为
克。
甲、乙、丙三个粮仓共存粮80吨,已知甲、乙两仓存粮之比为1:2,乙、丙两仓存粮之比是1:2.5,
则甲存粮____吨,乙存粮____吨,丙存粮_吨。
16、某种商品的标价为120元,若以九折降价出售,相对于进货价仍获利20%,该商品的进货价为
元
17、某工程要在x天内完成,现由甲先做3天,乙再参加合做,正好如期完成.若甲独做需12天完成,乙独做需8天完成,
则工期为
天。
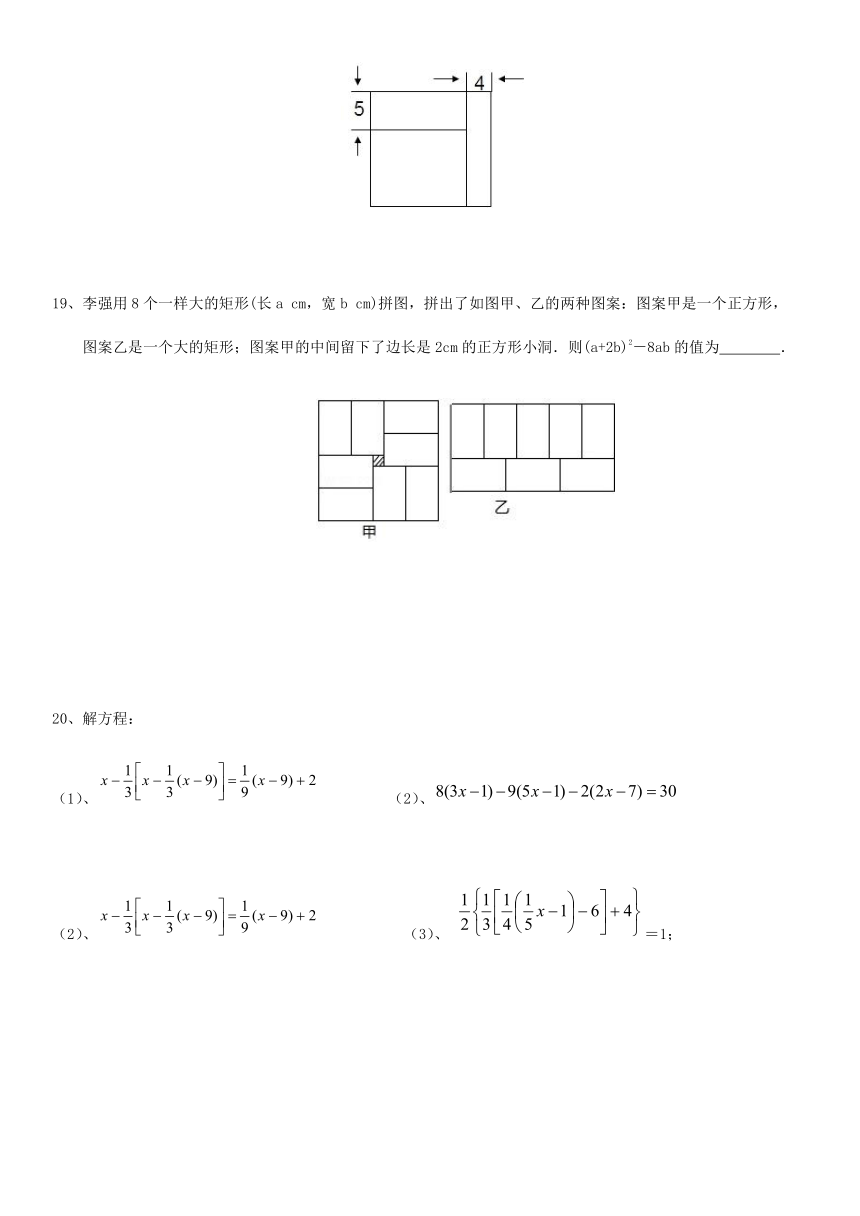
18、如图所示,小明将一个正方形的纸片剪去一个宽为4厘米的长条后,再从剩下的长方形纸片上剪去一个宽为5厘米的长条,如果两次剪下的长条面积正好相等,那么原来正方形的面积是
平方厘米。
李强用8个一样大的矩形(长a
cm,宽b
cm)拼图,拼出了如图甲、乙的两种图案:图案甲是一个正方形,
图案乙是一个大的矩形;图案甲的中间留下了边长是2cm的正方形小洞.则(a+2b)2-8ab的值为
.
20、解方程:
(1)、
(2)、
(2)、
(3)、
=1;
(3)、.
(4)、
(5)、2{3[4(5x-1)-8]-20}-7=1;
(6)、
(7)
(8)-=;
21、已知关于x的方程=x+与=3x
-2的解互为倒数,求m的值。
22、若关于x的方程=2+无论k为何值,方程的解总是x=1,求a,b的值.
23、阅读与探究:我们知道分数写为小数即,反之,无限循环小数写成分数即.
一般地,任何一个无限循环小数都可以写成分数形式.
现在就以为例进行探究:
设:,由:…,得:
…,(1)
根据等式性质得:
…,(2)
(2)-(1)
得:……,
即:,解方程得:,
所以:.
请仿照上述例题:
把无限循环小数写成分数,即
.
你能化无限循环小数为分数吗?请完成你的探究过程.
24、阅读下列例题.
解方程:|5x|=1.
①当5x>0时,原方程可化为一元一次方程5x=1,它的解是x==;
②当5x<0时,原方程可化为一元一次方程一5x=1.
它的解是x=一.
所以原方程的解是x=或x=一.
根据上面的解题过程,求解方程:|x一3
|=2.
25、已知关于x的方程kx+m=(2k一1)x+4,当k、m为何值时(1)方程有唯一解;(2)方程有无数个解;(3)方程无解.
26、.a※b是新规定的这样一种运算法则:a※b=a2+2ab,例如3※(-2)=32+2×3×(-2)=-3
(1)试求(-2)※3的值
(2)若1※x=3
,
求x的值
(3)若(-2)※x=-2+x
,
求x的值
27、一个大人一餐能吃四个面包,四个幼儿一餐只吃一个面包,现有大人和幼儿共100人,一餐刚好吃100个面包,这100人中大人和幼儿各有多少人?
28、小明和小亮去商店买东西,他们所带的钱数之比为7:6,小明用掉50元,小亮用掉60元,二人余下的钱数之比是3:2,他们原各有多少钱?
29、某工厂第一车间人数比第二车间人数的还少30人,如果从第二车间调10人到第一车间,那么第一车间的人数是第二车间人数的,求各车间原有的人数.
30、在一条路的两旁植树,若每隔3米植一棵,则剩3棵;若每隔2.5米植一棵,则缺少77棵,已知马路的长恰好是15米的整数倍,求这段马路的长。
31、如图,沿着边长为120米的正方形,A→B→C→D→A
……
的方向,甲以45米/分的速度,乙以60米/分的速度分别从A、B出发,经过多长时间,乙第一次追上甲?当乙第一次追上甲时,在正方形的哪个位置?
32、己知A、B、C、D四个车站的位置如图所示.
(1)求A、D两站之间的距离;(用含a、b的代数式表示)
(2)一辆汽车从A站出发,每小时行驶60千米,经过B站到达C站(在B站没有停留).所用时间为小时.汽车在C站短暂停留后,继续以相同速度行驶,再行驶2小时到达D站,求a,b的值以及汽车从B站行驶到C站一共用了多少小时?
如图,在长方形ABCD中,AB=12厘米,BC=6厘米,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;
点Q沿DA边从点D开始向点A以1厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间,那么:
(1)如图1,当t为何值时,线段AQ的长度等于线段AP的长度?
(2)如图2,当t为何值时,AQ与AP的长度之和是长方形ABCD周长的?
(3)如图3,点P到达B后继续运动,到达C点后停止运动;Q到达A后也继续运动,
当P点停止运动的同时点Q也停
止运动.当t为何值时,线段AQ的长度等于线段CP长度的一半?
问题一:如图1,已知A,C两点之间的距离为20
cm,甲,乙两点分别从相距5cm的A,B两点同时出发
到C点,若甲的速度为5
cm/s,乙的速度为3
cm/s,设乙运动时间为x(s),
甲乙两点之间距离为y(cm).
(1)谁先到C:
.
(2)当0<x<4时甲乙的距离=
(3)甲到C后甲,乙的距离=
问题二:如图2,若将上述线段AC弯曲后视作钟表外围的一部分,线段AB正好对应钟表上的弧AB
(1小时的间隔),易知∠AOB=30°.
分针OD指向圆周上的点的速度为每分钟转动
cm;时针OE指向圆周上的点的速度
为每分钟转动
cm.
(2)若从5:00起计时,求几分钟后分针与时针第一次重合.
35、如图,在数轴上点A表示的数是﹣3,点B在点A的右侧,且到点A的距离是18;点C在点A与点B之间,且到点B的距离是到点A距离的2倍.
(1)点B表示的数是
;点C表示的数是
;
(2)若点P从点A出发,沿数轴以每秒4个单位长度的速度向右匀速运动;同时,点Q从点B出发,沿数轴以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒,在运动过程中,当t为何值时,点P与点Q之间的距离为6?
(3)在(2)的条件下,若点P与点C之间的距离表示为PC,点Q与点B之间的距离表示为QB,在运动过程中,是否存在某一时刻使得PC+QB=4?若存在,请求出此时点P表示的数;若不存在,请说明理由.
1、若x=1是关于x的方程mx+n=p-1的解,则(m+n-p)2021=______.
2、已知方程的解与关于的方程的解相等,则代数式a?+2a+2020的
值为
3、关于的方程的解比关于y的方程的解小2,则a的值为
4、如表所示,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2021个格子中的数为
5、如果不论是何值,总是关于的方程3(Rx+a)-2(2x-bR)=6的解,则
,
.
已知关于x的一元一次方程的解为,
那么关于y的一元一次方程的解为
.
7、已知方程,则代数式的值为
。
8、在公式中,已知,,=21,则=________.
9、当为整数
时,方程的解为正整数。
李强在解方程□
时,把“□”中的数字看错了,解得
,那么李强把“□”中的数字
看成了
.
11、对于有理数、,规定,若,则的值为
.
12、小明今年13岁,妈妈38岁,
年后,小明年龄是妈妈的.
13、某学生读一本书,第一天读全书的还多6页,第二天再读剩下的,还有100页没有读,则全书有
页
14、北京奥运会的金牌是用金、银和玉三种物质混合而建的,它的总重量为244.5克,如果金、银、玉的重量之比为7:9:6,则金牌中的的重量为
克。
甲、乙、丙三个粮仓共存粮80吨,已知甲、乙两仓存粮之比为1:2,乙、丙两仓存粮之比是1:2.5,
则甲存粮____吨,乙存粮____吨,丙存粮_吨。
16、某种商品的标价为120元,若以九折降价出售,相对于进货价仍获利20%,该商品的进货价为
元
17、某工程要在x天内完成,现由甲先做3天,乙再参加合做,正好如期完成.若甲独做需12天完成,乙独做需8天完成,
则工期为
天。
18、如图所示,小明将一个正方形的纸片剪去一个宽为4厘米的长条后,再从剩下的长方形纸片上剪去一个宽为5厘米的长条,如果两次剪下的长条面积正好相等,那么原来正方形的面积是
平方厘米。
李强用8个一样大的矩形(长a
cm,宽b
cm)拼图,拼出了如图甲、乙的两种图案:图案甲是一个正方形,
图案乙是一个大的矩形;图案甲的中间留下了边长是2cm的正方形小洞.则(a+2b)2-8ab的值为
.
20、解方程:
(1)、
(2)、
(2)、
(3)、
=1;
(3)、.
(4)、
(5)、2{3[4(5x-1)-8]-20}-7=1;
(6)、
(7)
(8)-=;
21、已知关于x的方程=x+与=3x
-2的解互为倒数,求m的值。
22、若关于x的方程=2+无论k为何值,方程的解总是x=1,求a,b的值.
23、阅读与探究:我们知道分数写为小数即,反之,无限循环小数写成分数即.
一般地,任何一个无限循环小数都可以写成分数形式.
现在就以为例进行探究:
设:,由:…,得:
…,(1)
根据等式性质得:
…,(2)
(2)-(1)
得:……,
即:,解方程得:,
所以:.
请仿照上述例题:
把无限循环小数写成分数,即
.
你能化无限循环小数为分数吗?请完成你的探究过程.
24、阅读下列例题.
解方程:|5x|=1.
①当5x>0时,原方程可化为一元一次方程5x=1,它的解是x==;
②当5x<0时,原方程可化为一元一次方程一5x=1.
它的解是x=一.
所以原方程的解是x=或x=一.
根据上面的解题过程,求解方程:|x一3
|=2.
25、已知关于x的方程kx+m=(2k一1)x+4,当k、m为何值时(1)方程有唯一解;(2)方程有无数个解;(3)方程无解.
26、.a※b是新规定的这样一种运算法则:a※b=a2+2ab,例如3※(-2)=32+2×3×(-2)=-3
(1)试求(-2)※3的值
(2)若1※x=3
,
求x的值
(3)若(-2)※x=-2+x
,
求x的值
27、一个大人一餐能吃四个面包,四个幼儿一餐只吃一个面包,现有大人和幼儿共100人,一餐刚好吃100个面包,这100人中大人和幼儿各有多少人?
28、小明和小亮去商店买东西,他们所带的钱数之比为7:6,小明用掉50元,小亮用掉60元,二人余下的钱数之比是3:2,他们原各有多少钱?
29、某工厂第一车间人数比第二车间人数的还少30人,如果从第二车间调10人到第一车间,那么第一车间的人数是第二车间人数的,求各车间原有的人数.
30、在一条路的两旁植树,若每隔3米植一棵,则剩3棵;若每隔2.5米植一棵,则缺少77棵,已知马路的长恰好是15米的整数倍,求这段马路的长。
31、如图,沿着边长为120米的正方形,A→B→C→D→A
……
的方向,甲以45米/分的速度,乙以60米/分的速度分别从A、B出发,经过多长时间,乙第一次追上甲?当乙第一次追上甲时,在正方形的哪个位置?
32、己知A、B、C、D四个车站的位置如图所示.
(1)求A、D两站之间的距离;(用含a、b的代数式表示)
(2)一辆汽车从A站出发,每小时行驶60千米,经过B站到达C站(在B站没有停留).所用时间为小时.汽车在C站短暂停留后,继续以相同速度行驶,再行驶2小时到达D站,求a,b的值以及汽车从B站行驶到C站一共用了多少小时?
如图,在长方形ABCD中,AB=12厘米,BC=6厘米,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;
点Q沿DA边从点D开始向点A以1厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间,那么:
(1)如图1,当t为何值时,线段AQ的长度等于线段AP的长度?
(2)如图2,当t为何值时,AQ与AP的长度之和是长方形ABCD周长的?
(3)如图3,点P到达B后继续运动,到达C点后停止运动;Q到达A后也继续运动,
当P点停止运动的同时点Q也停
止运动.当t为何值时,线段AQ的长度等于线段CP长度的一半?
问题一:如图1,已知A,C两点之间的距离为20
cm,甲,乙两点分别从相距5cm的A,B两点同时出发
到C点,若甲的速度为5
cm/s,乙的速度为3
cm/s,设乙运动时间为x(s),
甲乙两点之间距离为y(cm).
(1)谁先到C:
.
(2)当0<x<4时甲乙的距离=
(3)甲到C后甲,乙的距离=
问题二:如图2,若将上述线段AC弯曲后视作钟表外围的一部分,线段AB正好对应钟表上的弧AB
(1小时的间隔),易知∠AOB=30°.
分针OD指向圆周上的点的速度为每分钟转动
cm;时针OE指向圆周上的点的速度
为每分钟转动
cm.
(2)若从5:00起计时,求几分钟后分针与时针第一次重合.
35、如图,在数轴上点A表示的数是﹣3,点B在点A的右侧,且到点A的距离是18;点C在点A与点B之间,且到点B的距离是到点A距离的2倍.
(1)点B表示的数是
;点C表示的数是
;
(2)若点P从点A出发,沿数轴以每秒4个单位长度的速度向右匀速运动;同时,点Q从点B出发,沿数轴以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒,在运动过程中,当t为何值时,点P与点Q之间的距离为6?
(3)在(2)的条件下,若点P与点C之间的距离表示为PC,点Q与点B之间的距离表示为QB,在运动过程中,是否存在某一时刻使得PC+QB=4?若存在,请求出此时点P表示的数;若不存在,请说明理由.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
