人教版九年级上册:24.1圆的有关性质练习 (word版,含答案)
文档属性
| 名称 | 人教版九年级上册:24.1圆的有关性质练习 (word版,含答案) | 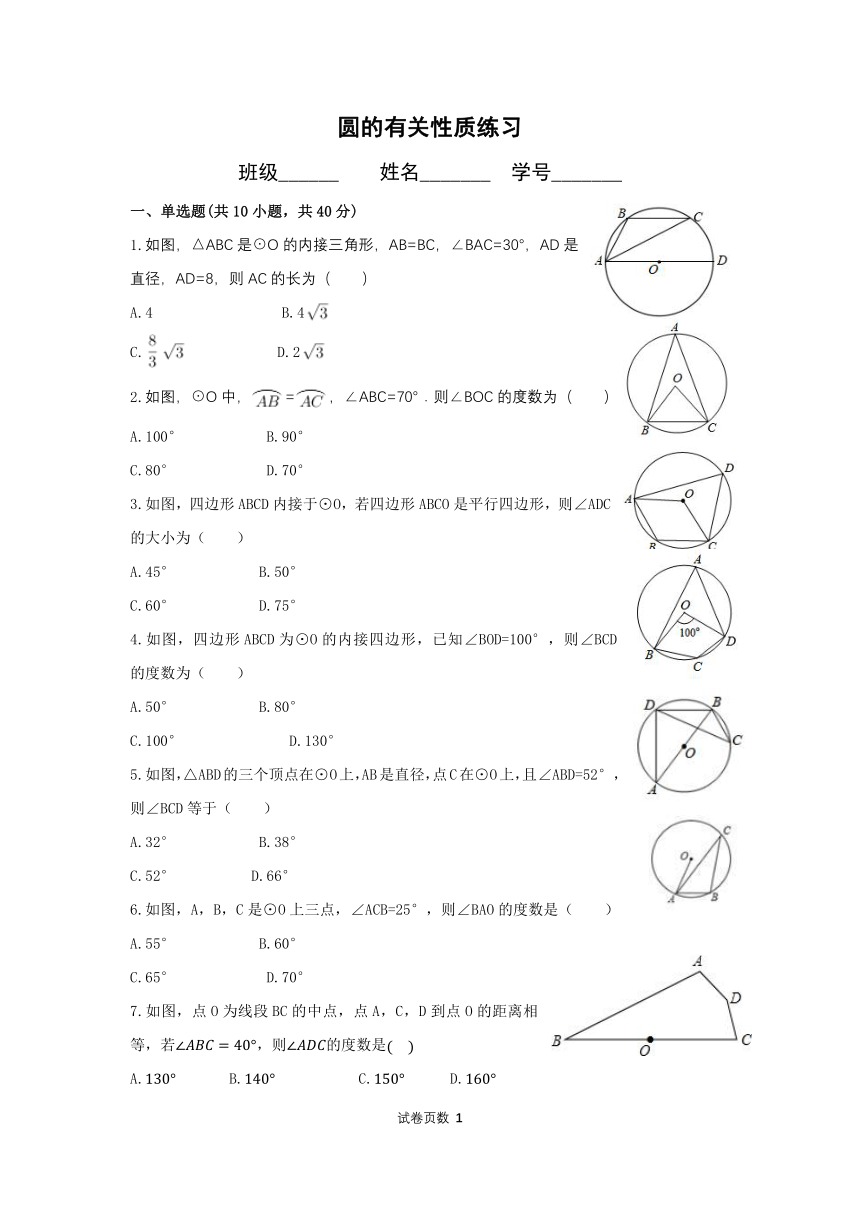 | |
| 格式 | zip | ||
| 文件大小 | 189.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-16 00:05:31 | ||
图片预览




文档简介
圆的有关性质练习
班级______
姓名_______
学号_______
一、单选题(共10小题,共40分)
1.如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为( )
A.4
B.4
C.
D.2
2.如图,⊙O中,=,∠ABC=70°.则∠BOC的度数为( )
A.100°
B.90°
C.80°
D.70°
3.如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )
A.45°
B.50°
C.60°
D.75°
4.如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )
A.50°
B.80°
C.100°
D.130°
5.如图,△ABD的三个顶点在⊙O上,AB是直径,点C在⊙O上,且∠ABD=52°,则∠BCD等于( )
A.32°
B.38°
C.52°
D.66°
6.如图,A,B,C是⊙O上三点,∠ACB=25°,则∠BAO的度数是( )
A.55°
B.60°
C.65°
D.70°
7.如图,点O为线段BC的中点,点A,C,D到点O的距离相等,若,则的度数是
A.
B.
C.
D.
8如图,AB是的直径,C,D是上的两点,且BC平分,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是
A.
B.
C.
D.
9.如图,BC是的直径,A,D是上的两点,连接AB,AD,BD,若,则的度数是
A.
B.
C.
D.
10.如图,在中,,,则的度数为
A.
B.
C.
D.
二、填空题(共6小题,共24分)
11.我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深ED=1寸,锯道长AB=1尺(1尺=10寸).问这根圆形木材的直径是______寸.
12.在△ABC中,若AB=6,∠ACB=45°.则△ABC的面积的最大值为______.
13.如图,AC是圆内接四边形ABCD的一条对角线,点D关于AC的对称点E在边BC上连接若,则的度数为____.
14.如图,内接于,,,于点D,若的半径为2,则CD的长为________.
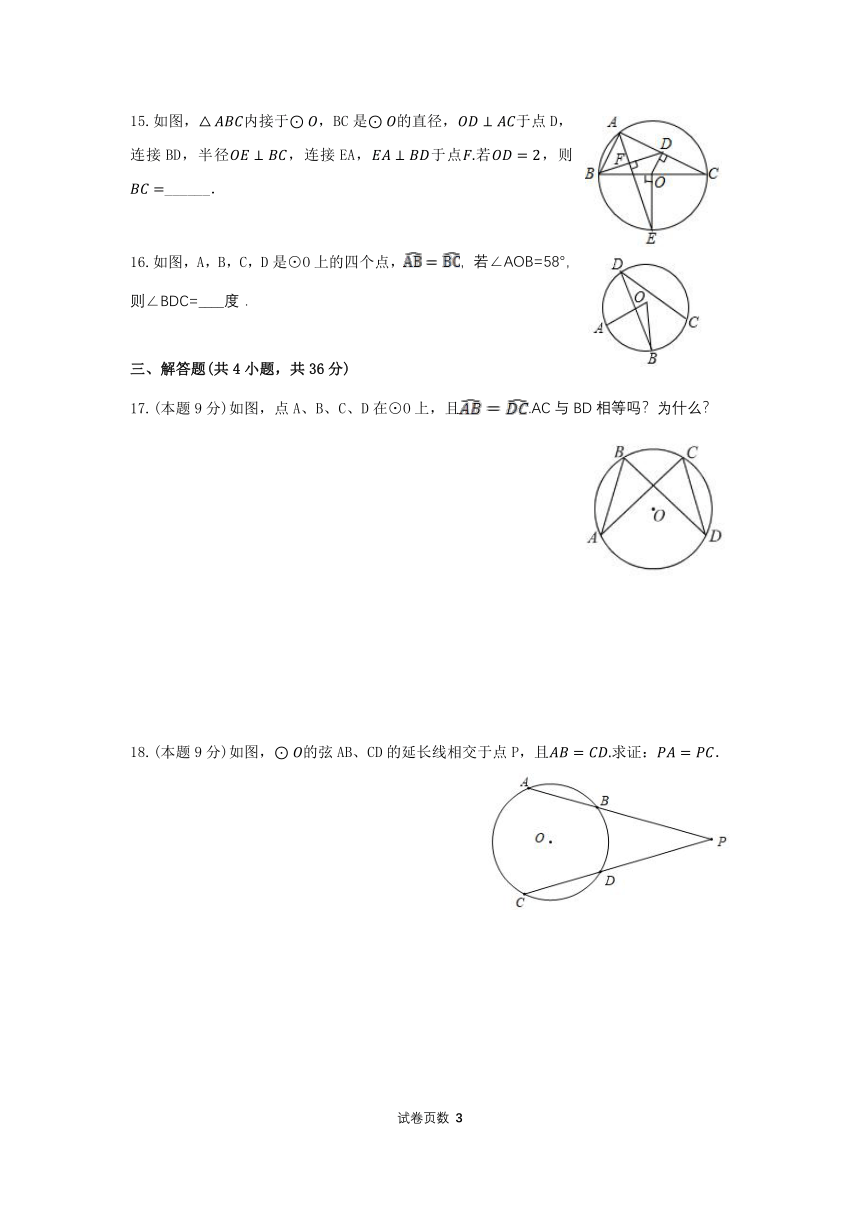
15.如图,内接于,BC是的直径,于点D,连接BD,半径,连接EA,于点若,则______.
16.如图,A,B,C,D是⊙O上的四个点,,若∠AOB=58°,则∠BDC=____度.
三、解答题(共4小题,共36分)
17.(本题9分)如图,点A、B、C、D在⊙O上,且.AC与BD相等吗?为什么?
18.(本题9分)如图,的弦AB、CD的延长线相交于点P,且求证:.
19.(本题9分)如图,AB是⊙O的直径,CD是⊙O的弦,,P是上一点(不与点C、D重合).∠APC与∠APD相等吗?为什么?
20.(本题9分)如图所示,自⊙O上一点C向弦AB作垂线段CD,求证:∠ACD=∠BCO.
圆的有关性质练习
参考答案与试题解析
1.【答案】:B;
【解析】:
解:连接CD,
∵AB=BC,∠BAC=30°,
∴∠ACB=∠BAC=30°,
∴∠B=180°-30°-30°=120°,
∴∠D=180°-∠B=60°,
∴∠CAD=30°,
∵AD是直径,
∴∠ACD=90°,
∵AD=8,
∴CD=AD=4,
∴AC===4,
故选:B.
连接CD,根据等腰三角形的性质得到∠ACB=∠BAC=30°,根据圆内接四边形的性质得到∠D=180°-∠B=60°,求得∠CAD=30°,根据直角三角形的性质即可得到结论.
本题考查了三角形的外接圆与外心,圆周角定理,含30°角的直角三角形的性质,勾股定理,正确的识别图形是解题的关键.
2.【答案】:C;
【解析】:
解:∵=,
∴∠ABC=∠ACB=70°,
∴∠A=180°-70°-70°=40°,
∴∠BOC=2∠A=80°.
故选:C.
先根据圆周角定理得到∠ABC=∠ACB=70°,再利用三角形内角和计算出∠A=40°,然后根据圆周角定理得到∠BOC的度数.
本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
3.【答案】:C;
【解析】:设∠ADC的度数=α,∠ABC的度数=β;
∵四边形ABCO是平行四边形,
∴∠ABC=∠AOC=β;
∵∠ADC=∠AOC,∠ADC=α;而α+β=180°,
∴,
解得:β=120°,α=60°,∠ADC=60°,
故选:C.
4.【答案】:D;
【解析】:∵∠BOD=100°,
∴∠BAD=100°÷2=50°,
∴∠BCD=180°﹣∠BAD
=180°﹣50°
=130°
故选:D.
5.【答案】:B;
【解析】:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ABD=52°,
∴∠A=90°﹣∠ABD=38°;
∴∠BCD=∠A=38°.
故选:B.
6.【答案】:C;
【解析】:连接OB,
∵∠ACB=25°,
∴∠AOB=2×25°=50°,
由OA=OB,
∴∠BAO=∠ABO,
∴∠BAO=(180°﹣50°)=65°.
故选:C.
7.【答案】:B;
【解析】:由题意得到,作出圆O,如图所示,
四边形ABCD为圆O的内接四边形,
,
,
,
故选:B.
8.【答案】:C;
【解析】:是的直径,BC平分,
,,
,
,
,
,
,选项A成立;
,选项B成立;
,选项D成立;
和中,没有相等的边,
与不全等,选项C不成立;
故选:C.
9.【答案】:A;
【解析】:连接AC,如图,
是的直径,
,
,
.
故答案为.
故选:A.
10.【答案】:B;
【解析】:连接OA、OC,
,,
,
都是半径,
.
故选:B.
11.【答案】:26;
【解析】:
解:由题意可知OE⊥AB,
∵OE为⊙O半径,
∴尺=5寸,
设半径OA=OE=r,
∵ED=1,
∴OD=r-1,
则Rt△OAD中,根据勾股定理可得:(r-1)2+52=r2,
解得:r=13,
∴木材直径为26寸;
故答案为:26.
根据题意可得OE⊥AB,由垂径定理可得尺=5寸,设半径OA=OE=r,则OD=r-1,在Rt△OAD中,根据勾股定理可得:(r-1)2+52=r2,解方程可得出木材半径,即可得出木材直径.
本题考查垂径定理结合勾股定理计算半径长度.如果题干中出现弦的垂线或者弦的中点,则可验证是否满足垂径定理;与圆有关的题目中如果求弦长或者求半径直径,也可以从题中寻找是否有垂径定理,然后构造直角三角形,用勾股定理求解.
12.【答案】:9+9;
【解析】:
解:作△ABC的外接圆⊙O,过C作CM⊥AB于M,
∵弦AB已确定,
∴要使△ABC的面积最大,只要CM取最大值即可,
如图所示,当CM过圆心O时,CM最大,
∵CM⊥AB,CM过O,
∴AM=BM(垂径定理),
∴AC=BC,
∵∠AOB=2∠ACB=2×45°=90°,
∴OM=AM=AB==3,
∴OA==3,
∴CM=OC+OM=3+3,
∴S△ABC=AB?CM=×6×(3+3)=9+9.
故答案为:9+9.
首先过C作CM⊥AB于M,由弦AB已确定,可得要使△ABC的面积最大,只要CM取最大值即可,即可得当CM过圆心O时,CM最大,然后由圆周角定理,证得△AOB是等腰直角三角形,则可求得CM的长,继而求得答案.
此题考查了三角形的外接圆与外心,圆周角定理以及等腰直角三角形性质.注意得到当CM过圆心O时,CM最大是关键.
13.【答案】:
;
【解析】:圆内接四边形ABCD,
,
点D关于AC的对称点E在边BC上,
,
.
故答案为:.
14.【答案】:
;
【解析】:连接CO并延长交于E,连接BE,
则,,
的半径为2,
,
,
,,
,
故答案为:.
15.【答案】:
;
【解析】:,
,
,
,
是的直径,
,
,
,
,
,
,
,
,
,
,
.
故答案为:.
16.【答案】:29;
【解析】:根据∠BDC=∠BOC求解即可;
连接OC.
∵,,
∴∠AOB=∠BOC=58°,
∴∠BDC=∠BOC=29°,
故答案为:29.
17.【答案】:解:AC与BD相等.
理由:∵
∴
即
∴
;
【解析】:根据,可得,再由在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对的其余各组量都分别相等即可证得AC与BD相等.
18.【答案】:证明:连接AC,
,
,
,即,
,
.
;
【解析】:连接AC,由圆心角、弧、弦的关系得出,进而得出,根据等弧所对的圆周角相等得出,根据等角对等边证得结论.
19.【答案】:解:相等.
理由:∵弦,AB是直径,
∴,
∴.
;
【解析】:由垂径定理知;当P在劣弧CD上时,∠APC和∠APD所对的是等弧,因此它们相等.
20.【答案】:证明:延长CO交⊙O于E点,连结BE.则∠CAB=∠CEB.
∵CE为⊙O的直径,
∴∠CBE=90°,
∴∠ADC=∠CBE=90°.
∵∠CAD+∠ADC+∠ACD=180°,
∠CEB+∠CBE+∠BCO=180°,
∴∠ACD=∠BCO.;
【解析】:延长CO交⊙O于E点,连结BE.根据同弧所对的圆周角相等得出∠CAB=∠CEB,由CE为⊙O的直径,根据直径所对的圆周角是直角得出∠CBE=90°,那么∠ADC=∠CBE=90°.然后根据三角形内角和定理得到∠CAD+∠ADC+∠ACD=180°,∠CEB+∠CBE+∠BCO=180°,利用等式的性质即可得出∠ACD=∠BCO.
试卷页数
班级______
姓名_______
学号_______
一、单选题(共10小题,共40分)
1.如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为( )
A.4
B.4
C.
D.2
2.如图,⊙O中,=,∠ABC=70°.则∠BOC的度数为( )
A.100°
B.90°
C.80°
D.70°
3.如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )
A.45°
B.50°
C.60°
D.75°
4.如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )
A.50°
B.80°
C.100°
D.130°
5.如图,△ABD的三个顶点在⊙O上,AB是直径,点C在⊙O上,且∠ABD=52°,则∠BCD等于( )
A.32°
B.38°
C.52°
D.66°
6.如图,A,B,C是⊙O上三点,∠ACB=25°,则∠BAO的度数是( )
A.55°
B.60°
C.65°
D.70°
7.如图,点O为线段BC的中点,点A,C,D到点O的距离相等,若,则的度数是
A.
B.
C.
D.
8如图,AB是的直径,C,D是上的两点,且BC平分,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是
A.
B.
C.
D.
9.如图,BC是的直径,A,D是上的两点,连接AB,AD,BD,若,则的度数是
A.
B.
C.
D.
10.如图,在中,,,则的度数为
A.
B.
C.
D.
二、填空题(共6小题,共24分)
11.我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深ED=1寸,锯道长AB=1尺(1尺=10寸).问这根圆形木材的直径是______寸.
12.在△ABC中,若AB=6,∠ACB=45°.则△ABC的面积的最大值为______.
13.如图,AC是圆内接四边形ABCD的一条对角线,点D关于AC的对称点E在边BC上连接若,则的度数为____.
14.如图,内接于,,,于点D,若的半径为2,则CD的长为________.
15.如图,内接于,BC是的直径,于点D,连接BD,半径,连接EA,于点若,则______.
16.如图,A,B,C,D是⊙O上的四个点,,若∠AOB=58°,则∠BDC=____度.
三、解答题(共4小题,共36分)
17.(本题9分)如图,点A、B、C、D在⊙O上,且.AC与BD相等吗?为什么?
18.(本题9分)如图,的弦AB、CD的延长线相交于点P,且求证:.
19.(本题9分)如图,AB是⊙O的直径,CD是⊙O的弦,,P是上一点(不与点C、D重合).∠APC与∠APD相等吗?为什么?
20.(本题9分)如图所示,自⊙O上一点C向弦AB作垂线段CD,求证:∠ACD=∠BCO.
圆的有关性质练习
参考答案与试题解析
1.【答案】:B;
【解析】:
解:连接CD,
∵AB=BC,∠BAC=30°,
∴∠ACB=∠BAC=30°,
∴∠B=180°-30°-30°=120°,
∴∠D=180°-∠B=60°,
∴∠CAD=30°,
∵AD是直径,
∴∠ACD=90°,
∵AD=8,
∴CD=AD=4,
∴AC===4,
故选:B.
连接CD,根据等腰三角形的性质得到∠ACB=∠BAC=30°,根据圆内接四边形的性质得到∠D=180°-∠B=60°,求得∠CAD=30°,根据直角三角形的性质即可得到结论.
本题考查了三角形的外接圆与外心,圆周角定理,含30°角的直角三角形的性质,勾股定理,正确的识别图形是解题的关键.
2.【答案】:C;
【解析】:
解:∵=,
∴∠ABC=∠ACB=70°,
∴∠A=180°-70°-70°=40°,
∴∠BOC=2∠A=80°.
故选:C.
先根据圆周角定理得到∠ABC=∠ACB=70°,再利用三角形内角和计算出∠A=40°,然后根据圆周角定理得到∠BOC的度数.
本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
3.【答案】:C;
【解析】:设∠ADC的度数=α,∠ABC的度数=β;
∵四边形ABCO是平行四边形,
∴∠ABC=∠AOC=β;
∵∠ADC=∠AOC,∠ADC=α;而α+β=180°,
∴,
解得:β=120°,α=60°,∠ADC=60°,
故选:C.
4.【答案】:D;
【解析】:∵∠BOD=100°,
∴∠BAD=100°÷2=50°,
∴∠BCD=180°﹣∠BAD
=180°﹣50°
=130°
故选:D.
5.【答案】:B;
【解析】:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ABD=52°,
∴∠A=90°﹣∠ABD=38°;
∴∠BCD=∠A=38°.
故选:B.
6.【答案】:C;
【解析】:连接OB,
∵∠ACB=25°,
∴∠AOB=2×25°=50°,
由OA=OB,
∴∠BAO=∠ABO,
∴∠BAO=(180°﹣50°)=65°.
故选:C.
7.【答案】:B;
【解析】:由题意得到,作出圆O,如图所示,
四边形ABCD为圆O的内接四边形,
,
,
,
故选:B.
8.【答案】:C;
【解析】:是的直径,BC平分,
,,
,
,
,
,
,选项A成立;
,选项B成立;
,选项D成立;
和中,没有相等的边,
与不全等,选项C不成立;
故选:C.
9.【答案】:A;
【解析】:连接AC,如图,
是的直径,
,
,
.
故答案为.
故选:A.
10.【答案】:B;
【解析】:连接OA、OC,
,,
,
都是半径,
.
故选:B.
11.【答案】:26;
【解析】:
解:由题意可知OE⊥AB,
∵OE为⊙O半径,
∴尺=5寸,
设半径OA=OE=r,
∵ED=1,
∴OD=r-1,
则Rt△OAD中,根据勾股定理可得:(r-1)2+52=r2,
解得:r=13,
∴木材直径为26寸;
故答案为:26.
根据题意可得OE⊥AB,由垂径定理可得尺=5寸,设半径OA=OE=r,则OD=r-1,在Rt△OAD中,根据勾股定理可得:(r-1)2+52=r2,解方程可得出木材半径,即可得出木材直径.
本题考查垂径定理结合勾股定理计算半径长度.如果题干中出现弦的垂线或者弦的中点,则可验证是否满足垂径定理;与圆有关的题目中如果求弦长或者求半径直径,也可以从题中寻找是否有垂径定理,然后构造直角三角形,用勾股定理求解.
12.【答案】:9+9;
【解析】:
解:作△ABC的外接圆⊙O,过C作CM⊥AB于M,
∵弦AB已确定,
∴要使△ABC的面积最大,只要CM取最大值即可,
如图所示,当CM过圆心O时,CM最大,
∵CM⊥AB,CM过O,
∴AM=BM(垂径定理),
∴AC=BC,
∵∠AOB=2∠ACB=2×45°=90°,
∴OM=AM=AB==3,
∴OA==3,
∴CM=OC+OM=3+3,
∴S△ABC=AB?CM=×6×(3+3)=9+9.
故答案为:9+9.
首先过C作CM⊥AB于M,由弦AB已确定,可得要使△ABC的面积最大,只要CM取最大值即可,即可得当CM过圆心O时,CM最大,然后由圆周角定理,证得△AOB是等腰直角三角形,则可求得CM的长,继而求得答案.
此题考查了三角形的外接圆与外心,圆周角定理以及等腰直角三角形性质.注意得到当CM过圆心O时,CM最大是关键.
13.【答案】:
;
【解析】:圆内接四边形ABCD,
,
点D关于AC的对称点E在边BC上,
,
.
故答案为:.
14.【答案】:
;
【解析】:连接CO并延长交于E,连接BE,
则,,
的半径为2,
,
,
,,
,
故答案为:.
15.【答案】:
;
【解析】:,
,
,
,
是的直径,
,
,
,
,
,
,
,
,
,
,
.
故答案为:.
16.【答案】:29;
【解析】:根据∠BDC=∠BOC求解即可;
连接OC.
∵,,
∴∠AOB=∠BOC=58°,
∴∠BDC=∠BOC=29°,
故答案为:29.
17.【答案】:解:AC与BD相等.
理由:∵
∴
即
∴
;
【解析】:根据,可得,再由在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对的其余各组量都分别相等即可证得AC与BD相等.
18.【答案】:证明:连接AC,
,
,
,即,
,
.
;
【解析】:连接AC,由圆心角、弧、弦的关系得出,进而得出,根据等弧所对的圆周角相等得出,根据等角对等边证得结论.
19.【答案】:解:相等.
理由:∵弦,AB是直径,
∴,
∴.
;
【解析】:由垂径定理知;当P在劣弧CD上时,∠APC和∠APD所对的是等弧,因此它们相等.
20.【答案】:证明:延长CO交⊙O于E点,连结BE.则∠CAB=∠CEB.
∵CE为⊙O的直径,
∴∠CBE=90°,
∴∠ADC=∠CBE=90°.
∵∠CAD+∠ADC+∠ACD=180°,
∠CEB+∠CBE+∠BCO=180°,
∴∠ACD=∠BCO.;
【解析】:延长CO交⊙O于E点,连结BE.根据同弧所对的圆周角相等得出∠CAB=∠CEB,由CE为⊙O的直径,根据直径所对的圆周角是直角得出∠CBE=90°,那么∠ADC=∠CBE=90°.然后根据三角形内角和定理得到∠CAD+∠ADC+∠ACD=180°,∠CEB+∠CBE+∠BCO=180°,利用等式的性质即可得出∠ACD=∠BCO.
试卷页数
同课章节目录
