人教版数学九年级上册24.1 圆的有关性质 同步练习(Word版 含答案)
文档属性
| 名称 | 人教版数学九年级上册24.1 圆的有关性质 同步练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 613.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-16 07:09:28 | ||
图片预览




文档简介
第二十四章
24.1 圆的有关性质
24.1.1 圆
1.下列说法中正确的是( )
(A)长度相等的弧是等弧
(B)半圆是弧
(C)半圆是圆中最长的弧
(D)优弧一定大于劣弧
2.半径为5的圆中,弦AB的长不可能是( )
(A)3
(B)5
(C)10
(D)12
3.如图,在△ABC中,∠ACB=90°,∠A=40°,以C为圆心,CB为半径的圆交AB于点D,连接CD,则∠ACD的度数为( )
第3题图
(A)10°
(B)15°
(C)20°
(D)25°
4.如图,AB是☉O的直径,D,C在☉O上,AD∥OC,∠DAC=30°,连接AC,则∠BOC等于( )
第4题图
(A)15°
(B)30°
(C)45°
(D)60°
5.下列说法:①半径是弦;②直径是弦;③过圆心的线段是直径;④弧分为优弧和劣弧;⑤半径相等的圆是等圆;其中正确的是 (填序号).?
6.如图,AB是☉O的直径,点C在☉O上,CD⊥AB,垂足为D,已知CD=4,OD=3,则AB的值为 .?
第6题图
7.如图,A,B,C是☉O上的三点,∠AOB=50°,∠OBC=40°,求∠OAC的度数.
8.平面上有☉O及一点A,点A到☉O上一点的距离最长为10
cm,最短为4
cm,则☉O的半径为 .?
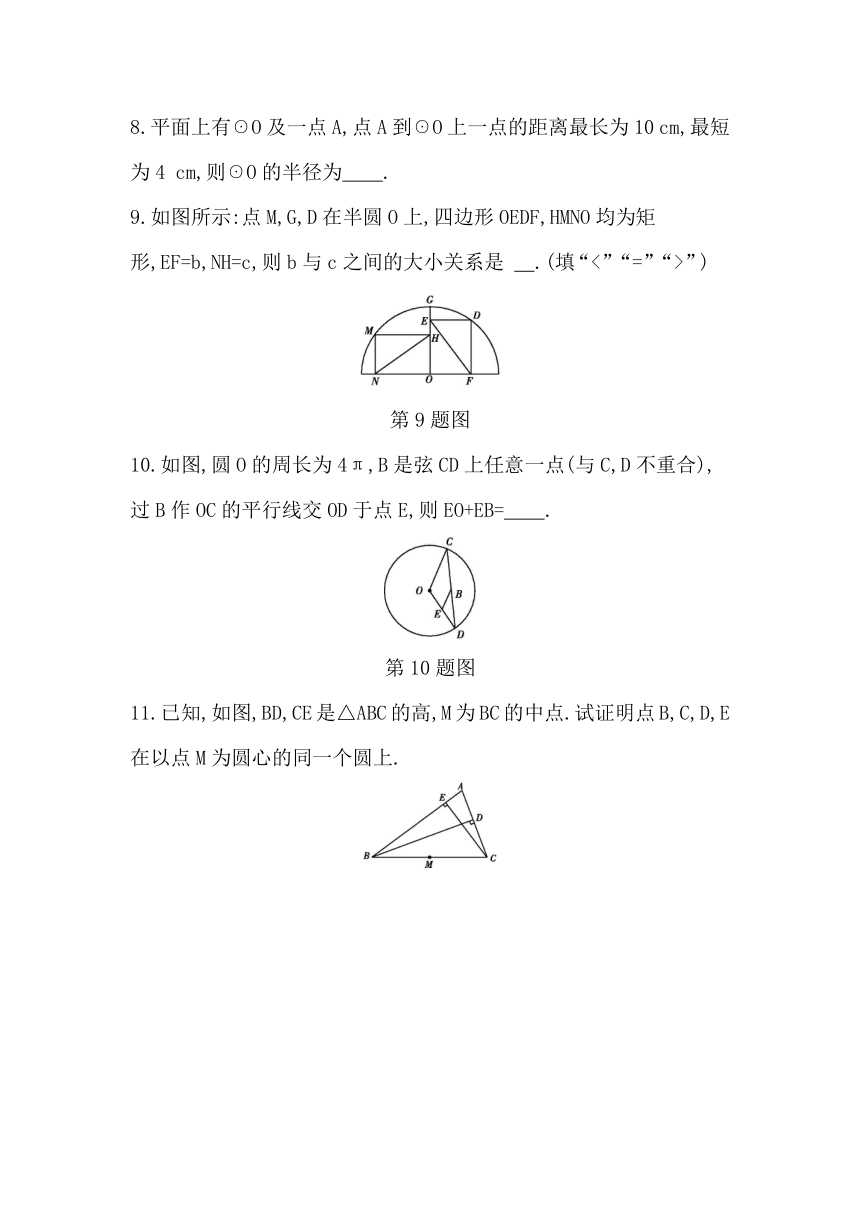
9.如图所示:点M,G,D在半圆O上,四边形OEDF,HMNO均为矩形,EF=b,NH=c,则b与c之间的大小关系是
.(填“<”“=”“>”)?
第9题图
10.如图,圆O的周长为4π,B是弦CD上任意一点(与C,D不重合),过B作OC的平行线交OD于点E,则EO+EB= .?
第10题图
11.已知,如图,BD,CE是△ABC的高,M为BC的中点.试证明点B,C,D,E在以点M为圆心的同一个圆上.
12.(教材拓展题)
如图,AB是☉O的直径,点C,D在☉O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
24.1.2 垂直于弦的直径
1.(2020潍坊期中)☉O的直径为10,圆心O到弦AB的距离为3,则弦AB的长是( )
(A)8
(B)7
(C)6
(D)4
2.如图,☉O的半径OA=6,以A为圆心,OA为半径的弧交☉O于B,C点,则BC等于( )
第2题图
(A)6
(B)6
(C)3
(D)3
3.(2019黄冈)如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,AB=40
m,点C是的中点,点D是AB的中点,且CD=
10
m,则这段弯路所在圆的半径为( )
(A)25
m
(B)24
m
(C)30
m
(D)60
m
第3题图
4.如图,AB为☉O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则☉O的半径为 .?
第4题图
5.如图,水平放置的圆柱形排水管的截面半径为10
cm,截面中有水部分弓形高为5
cm,则水面宽AB为 cm.?
第5题图
6.(2020广州期中)如图,在☉O中,相等的弦AB,AC互相垂直,点E是AC的中点,OD⊥AB于点D.求证:四边形AEOD是正方形.
7.(2019嘉兴)如图,在☉O中,弦
AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交☉O于点D,则CD的最大值为 .?
8.已知☉O的半径是
5
cm,弦AB∥CD,AB=6
cm,CD=8
cm,则AB与CD的距离是多少?
9.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为
16
cm2,求该半圆的半径.
第二十四章
24.1 圆的有关性质
24.1.1 圆
1.下列说法中正确的是( B )
(A)长度相等的弧是等弧
(B)半圆是弧
(C)半圆是圆中最长的弧
(D)优弧一定大于劣弧
2.半径为5的圆中,弦AB的长不可能是( D )
(A)3
(B)5
(C)10
(D)12
3.如图,在△ABC中,∠ACB=90°,∠A=40°,以C为圆心,CB为半径的圆交AB于点D,连接CD,则∠ACD的度数为( A )
第3题图
(A)10°
(B)15°
(C)20°
(D)25°
4.如图,AB是☉O的直径,D,C在☉O上,AD∥OC,∠DAC=30°,连接AC,则∠BOC等于( D )
第4题图
(A)15°
(B)30°
(C)45°
(D)60°
5.下列说法:①半径是弦;②直径是弦;③过圆心的线段是直径;④弧分为优弧和劣弧;⑤半径相等的圆是等圆;其中正确的是 ②⑤ (填序号).?
6.如图,AB是☉O的直径,点C在☉O上,CD⊥AB,垂足为D,已知CD=4,OD=3,则AB的值为 10 .?
第6题图
7.如图,A,B,C是☉O上的三点,∠AOB=50°,∠OBC=40°,求∠OAC的度数.
解:如图,连接OC,因为OB=OC,
所以∠OCB=∠OBC=40°.
所以∠BOC=180°-∠OBC-∠OCB
=180°-40°-40°=100°.
所以∠AOC=∠AOB+∠BOC=50°+100°=150°.
又因为OA=OC,
所以∠OAC==15°.
8.平面上有☉O及一点A,点A到☉O上一点的距离最长为10
cm,最短为4
cm,则☉O的半径为 3
cm或7
cm .?
9.如图所示:点M,G,D在半圆O上,四边形OEDF,HMNO均为矩形,EF=b,NH=c,则b与c之间的大小关系是b = c.(填“<”“=”“>”)?
第9题图
10.如图,圆O的周长为4π,B是弦CD上任意一点(与C,D不重合),过B作OC的平行线交OD于点E,则EO+EB= 2 .?
第10题图
11.已知,如图,BD,CE是△ABC的高,M为BC的中点.试证明点B,C,D,E在以点M为圆心的同一个圆上.
证明:如图,连接ME,MD,
因为BD,CE分别是△ABC的高,
所以△EBC和△DBC都是直角三角形.
因为M为斜边BC的中点,
所以ME=MD=BC=MB=MC.
所以点B,C,D,E都在以点M为圆心的同一个圆上.
12.(教材拓展题)
如图,AB是☉O的直径,点C,D在☉O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
解:AC与BD相等.
理由如下:连接OC,OD,如图.
因为OA=OB,AE=BF,
所以OA-AE=OB-BF,
即OE=OF.
因为CE⊥AB,DF⊥AB,
所以∠OEC=∠OFD=90°.
在Rt△OEC和Rt△OFD中,
所以Rt△OEC≌Rt△OFD(HL).
所以CE=DF.
在△AEC与△BFD中,
所以△AEC≌△BFD(SAS).所以AC=BD.
24.1.2 垂直于弦的直径
1.(2020潍坊期中)☉O的直径为10,圆心O到弦AB的距离为3,则弦AB的长是( A )
(A)8
(B)7
(C)6
(D)4
2.如图,☉O的半径OA=6,以A为圆心,OA为半径的弧交☉O于B,C点,则BC等于( A )
第2题图
(A)6
(B)6
(C)3
(D)3
3.(2019黄冈)如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,AB=40
m,点C是的中点,点D是AB的中点,且CD=
10
m,则这段弯路所在圆的半径为( A )
(A)25
m
(B)24
m
(C)30
m
(D)60
m
第3题图
4.如图,AB为☉O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则☉O的半径为 5 .?
第4题图
5.如图,水平放置的圆柱形排水管的截面半径为10
cm,截面中有水部分弓形高为5
cm,则水面宽AB为 10 cm.?
第5题图
6.(2020广州期中)如图,在☉O中,相等的弦AB,AC互相垂直,点E是AC的中点,OD⊥AB于点D.求证:四边形AEOD是正方形.
证明:因为OD⊥AB于点D,
所以AD=AB,
因为AE是AC的中点,
所以OE⊥AC,
所以∠ADO=∠AEO=90°,
因为AB⊥AC,所以∠DAE=90°,
所以四边形AEOD是矩形,
因为AB=AC,
所以AD=AE,
所以四边形AEOD是正方形.
7.(2019嘉兴)如图,在☉O中,弦
AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交☉O于点D,则CD的最大值为 .?
8.已知☉O的半径是
5
cm,弦AB∥CD,AB=6
cm,CD=8
cm,则AB与CD的距离是多少?
解:分为两种情况:
①当AB和CD在O的同旁时,如图(1),过O作OE⊥AB于E,交CD于F,连接OA,OC,
因为AB∥CD,
所以OF⊥CD.
由垂径定理得AE=AB=3
cm,CF=CD=4
cm.
在Rt△OAE中,由勾股定理,得
OE===4(cm).
同理求出OF=3
cm.
所以EF=4-3=1(cm).
②当AB和CD在O的两侧时,如图(2),同理求出OE=4
cm,OF=3
cm,
所以EF=4+3=7(cm).
综上所述,AB与CD的距离是1
cm或7
cm.
9.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为
16
cm2,求该半圆的半径.
解:如图,连接OA,OB,
设OD=x
cm,则AD=2x
cm,
因为小正方形的面积为16
cm2,
所以DC=CB=4
cm,
在Rt△OAD和Rt△OBC中,由勾股定理,得
x2+(2x)2=42+(4+x)2,
解得x1=4,x2=-2(舍去).
所以OD=4
cm,AD=2×4=8(cm),
所以即该半圆的半径为4
cm.
AO===4(cm).
24.1 圆的有关性质
24.1.1 圆
1.下列说法中正确的是( )
(A)长度相等的弧是等弧
(B)半圆是弧
(C)半圆是圆中最长的弧
(D)优弧一定大于劣弧
2.半径为5的圆中,弦AB的长不可能是( )
(A)3
(B)5
(C)10
(D)12
3.如图,在△ABC中,∠ACB=90°,∠A=40°,以C为圆心,CB为半径的圆交AB于点D,连接CD,则∠ACD的度数为( )
第3题图
(A)10°
(B)15°
(C)20°
(D)25°
4.如图,AB是☉O的直径,D,C在☉O上,AD∥OC,∠DAC=30°,连接AC,则∠BOC等于( )
第4题图
(A)15°
(B)30°
(C)45°
(D)60°
5.下列说法:①半径是弦;②直径是弦;③过圆心的线段是直径;④弧分为优弧和劣弧;⑤半径相等的圆是等圆;其中正确的是 (填序号).?
6.如图,AB是☉O的直径,点C在☉O上,CD⊥AB,垂足为D,已知CD=4,OD=3,则AB的值为 .?
第6题图
7.如图,A,B,C是☉O上的三点,∠AOB=50°,∠OBC=40°,求∠OAC的度数.
8.平面上有☉O及一点A,点A到☉O上一点的距离最长为10
cm,最短为4
cm,则☉O的半径为 .?
9.如图所示:点M,G,D在半圆O上,四边形OEDF,HMNO均为矩形,EF=b,NH=c,则b与c之间的大小关系是
.(填“<”“=”“>”)?
第9题图
10.如图,圆O的周长为4π,B是弦CD上任意一点(与C,D不重合),过B作OC的平行线交OD于点E,则EO+EB= .?
第10题图
11.已知,如图,BD,CE是△ABC的高,M为BC的中点.试证明点B,C,D,E在以点M为圆心的同一个圆上.
12.(教材拓展题)
如图,AB是☉O的直径,点C,D在☉O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
24.1.2 垂直于弦的直径
1.(2020潍坊期中)☉O的直径为10,圆心O到弦AB的距离为3,则弦AB的长是( )
(A)8
(B)7
(C)6
(D)4
2.如图,☉O的半径OA=6,以A为圆心,OA为半径的弧交☉O于B,C点,则BC等于( )
第2题图
(A)6
(B)6
(C)3
(D)3
3.(2019黄冈)如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,AB=40
m,点C是的中点,点D是AB的中点,且CD=
10
m,则这段弯路所在圆的半径为( )
(A)25
m
(B)24
m
(C)30
m
(D)60
m
第3题图
4.如图,AB为☉O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则☉O的半径为 .?
第4题图
5.如图,水平放置的圆柱形排水管的截面半径为10
cm,截面中有水部分弓形高为5
cm,则水面宽AB为 cm.?
第5题图
6.(2020广州期中)如图,在☉O中,相等的弦AB,AC互相垂直,点E是AC的中点,OD⊥AB于点D.求证:四边形AEOD是正方形.
7.(2019嘉兴)如图,在☉O中,弦
AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交☉O于点D,则CD的最大值为 .?
8.已知☉O的半径是
5
cm,弦AB∥CD,AB=6
cm,CD=8
cm,则AB与CD的距离是多少?
9.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为
16
cm2,求该半圆的半径.
第二十四章
24.1 圆的有关性质
24.1.1 圆
1.下列说法中正确的是( B )
(A)长度相等的弧是等弧
(B)半圆是弧
(C)半圆是圆中最长的弧
(D)优弧一定大于劣弧
2.半径为5的圆中,弦AB的长不可能是( D )
(A)3
(B)5
(C)10
(D)12
3.如图,在△ABC中,∠ACB=90°,∠A=40°,以C为圆心,CB为半径的圆交AB于点D,连接CD,则∠ACD的度数为( A )
第3题图
(A)10°
(B)15°
(C)20°
(D)25°
4.如图,AB是☉O的直径,D,C在☉O上,AD∥OC,∠DAC=30°,连接AC,则∠BOC等于( D )
第4题图
(A)15°
(B)30°
(C)45°
(D)60°
5.下列说法:①半径是弦;②直径是弦;③过圆心的线段是直径;④弧分为优弧和劣弧;⑤半径相等的圆是等圆;其中正确的是 ②⑤ (填序号).?
6.如图,AB是☉O的直径,点C在☉O上,CD⊥AB,垂足为D,已知CD=4,OD=3,则AB的值为 10 .?
第6题图
7.如图,A,B,C是☉O上的三点,∠AOB=50°,∠OBC=40°,求∠OAC的度数.
解:如图,连接OC,因为OB=OC,
所以∠OCB=∠OBC=40°.
所以∠BOC=180°-∠OBC-∠OCB
=180°-40°-40°=100°.
所以∠AOC=∠AOB+∠BOC=50°+100°=150°.
又因为OA=OC,
所以∠OAC==15°.
8.平面上有☉O及一点A,点A到☉O上一点的距离最长为10
cm,最短为4
cm,则☉O的半径为 3
cm或7
cm .?
9.如图所示:点M,G,D在半圆O上,四边形OEDF,HMNO均为矩形,EF=b,NH=c,则b与c之间的大小关系是b = c.(填“<”“=”“>”)?
第9题图
10.如图,圆O的周长为4π,B是弦CD上任意一点(与C,D不重合),过B作OC的平行线交OD于点E,则EO+EB= 2 .?
第10题图
11.已知,如图,BD,CE是△ABC的高,M为BC的中点.试证明点B,C,D,E在以点M为圆心的同一个圆上.
证明:如图,连接ME,MD,
因为BD,CE分别是△ABC的高,
所以△EBC和△DBC都是直角三角形.
因为M为斜边BC的中点,
所以ME=MD=BC=MB=MC.
所以点B,C,D,E都在以点M为圆心的同一个圆上.
12.(教材拓展题)
如图,AB是☉O的直径,点C,D在☉O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
解:AC与BD相等.
理由如下:连接OC,OD,如图.
因为OA=OB,AE=BF,
所以OA-AE=OB-BF,
即OE=OF.
因为CE⊥AB,DF⊥AB,
所以∠OEC=∠OFD=90°.
在Rt△OEC和Rt△OFD中,
所以Rt△OEC≌Rt△OFD(HL).
所以CE=DF.
在△AEC与△BFD中,
所以△AEC≌△BFD(SAS).所以AC=BD.
24.1.2 垂直于弦的直径
1.(2020潍坊期中)☉O的直径为10,圆心O到弦AB的距离为3,则弦AB的长是( A )
(A)8
(B)7
(C)6
(D)4
2.如图,☉O的半径OA=6,以A为圆心,OA为半径的弧交☉O于B,C点,则BC等于( A )
第2题图
(A)6
(B)6
(C)3
(D)3
3.(2019黄冈)如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,AB=40
m,点C是的中点,点D是AB的中点,且CD=
10
m,则这段弯路所在圆的半径为( A )
(A)25
m
(B)24
m
(C)30
m
(D)60
m
第3题图
4.如图,AB为☉O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则☉O的半径为 5 .?
第4题图
5.如图,水平放置的圆柱形排水管的截面半径为10
cm,截面中有水部分弓形高为5
cm,则水面宽AB为 10 cm.?
第5题图
6.(2020广州期中)如图,在☉O中,相等的弦AB,AC互相垂直,点E是AC的中点,OD⊥AB于点D.求证:四边形AEOD是正方形.
证明:因为OD⊥AB于点D,
所以AD=AB,
因为AE是AC的中点,
所以OE⊥AC,
所以∠ADO=∠AEO=90°,
因为AB⊥AC,所以∠DAE=90°,
所以四边形AEOD是矩形,
因为AB=AC,
所以AD=AE,
所以四边形AEOD是正方形.
7.(2019嘉兴)如图,在☉O中,弦
AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交☉O于点D,则CD的最大值为 .?
8.已知☉O的半径是
5
cm,弦AB∥CD,AB=6
cm,CD=8
cm,则AB与CD的距离是多少?
解:分为两种情况:
①当AB和CD在O的同旁时,如图(1),过O作OE⊥AB于E,交CD于F,连接OA,OC,
因为AB∥CD,
所以OF⊥CD.
由垂径定理得AE=AB=3
cm,CF=CD=4
cm.
在Rt△OAE中,由勾股定理,得
OE===4(cm).
同理求出OF=3
cm.
所以EF=4-3=1(cm).
②当AB和CD在O的两侧时,如图(2),同理求出OE=4
cm,OF=3
cm,
所以EF=4+3=7(cm).
综上所述,AB与CD的距离是1
cm或7
cm.
9.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为
16
cm2,求该半圆的半径.
解:如图,连接OA,OB,
设OD=x
cm,则AD=2x
cm,
因为小正方形的面积为16
cm2,
所以DC=CB=4
cm,
在Rt△OAD和Rt△OBC中,由勾股定理,得
x2+(2x)2=42+(4+x)2,
解得x1=4,x2=-2(舍去).
所以OD=4
cm,AD=2×4=8(cm),
所以即该半圆的半径为4
cm.
AO===4(cm).
同课章节目录
