2020-2021学年上海市浦东新区第四教育署七年级上学期调研数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年上海市浦东新区第四教育署七年级上学期调研数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 337.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-16 06:49:59 | ||
图片预览




文档简介
2020-2021学年上海市浦东新区第四教育署七年级(上)调研数学试卷
一、选择题(共6小题).
1.(2分)下列不能表示“2a”的意义的是( )
A.2的a倍 B.a的2倍 C.2个a相加 D.2个a相乘
2.(2分)下列式子中,单项式是( )
A.3a+1 B. C.3a D.x=1
3.(2分)下列各选项中是同类项的是( )
A.﹣a2b和ab2 B.a2和22
C.﹣ab2和2b2a D.2ab和2xy
4.(2分)下列运算正确( )
A.a2+a3=a5 B.a2?a3=a6
C.(a2)3=a8 D.(﹣a)2?a3=a5
5.(2分)如果M=x2+6x+22,N=﹣x2+6x﹣3,那么M与N的大小关系是( )
A.M>N B.M<N C.M=N D.无法确定
6.(2分)按下面的程序计算,如果输入x的值是30,那么输出的结果为( )
A.470 B.471 C.118 D.119
二、填空题(共12小题).
7.(3分)单项式的次数是 .
8.(3分)x、y两数的平方和减去它们的积的2倍,用代数式表示为 .
9.(3分)计算:x2?x3?x4= .
10.(3分)计算:(x2)5= .
11.(3分)比较大小:25 43(填>,<或=).
12.(3分)化简3a﹣[a﹣2(a﹣b)]+b,结果是 .
13.(3分)当1<a<2时,代数式|a﹣2|+|1﹣a|的值是 .
14.(3分)若a与b互为相反数,m和n互为倒数,则= .
15.(3分)已知单项式﹣anb3与单项式﹣2a2bm﹣2是同类项,则m﹣n= .
16.(3分)若9×32m×33m=322,则m的值为 .
17.(3分)如果两个关于x的多项式4x2﹣bx﹣5+c与ax2+2x﹣3相等,则a+bc= .
18.(3分)如图,四张大小不一的四方形纸片分别放置于矩形的四个角落,其中①和②纸片既不重叠也无空隙.已知矩形ABCD的周长为a,阴影部分的周长为b那么以下四个正方形中 号正方形的边长可以直接用a、b表示,结果为 .
三、解答题(本大题共8小题,第19至24题每题6分,第25、26题每题8分,共52分)
19.(6分)计算:9m2﹣4(2m2﹣3mn+n2)+4n2.
20.(6分)计算:x2?x3+(﹣x)5+(x2)3.
21.(6分)(a﹣b)2?(b﹣a)3?(b﹣a)(结果用幂的形式表示)
22.(6分)已知多项式.
(1)把这个多项式按x的降幂重新排列;
(2)请指出该多项式的次数,并写出它的二次项和常数项.
23.(6分)已知:m2+mn=30,mn﹣n2=﹣10,求下列代数式的值:
(1)m2+2mn﹣n2;
(2)m2+n2﹣7.
24.(6分)化简求值,其中x=2,y=﹣0.5.
25.(8分)已知(x3)n+1=(xn﹣1)4?(x3)2,求(﹣n2)3的值.
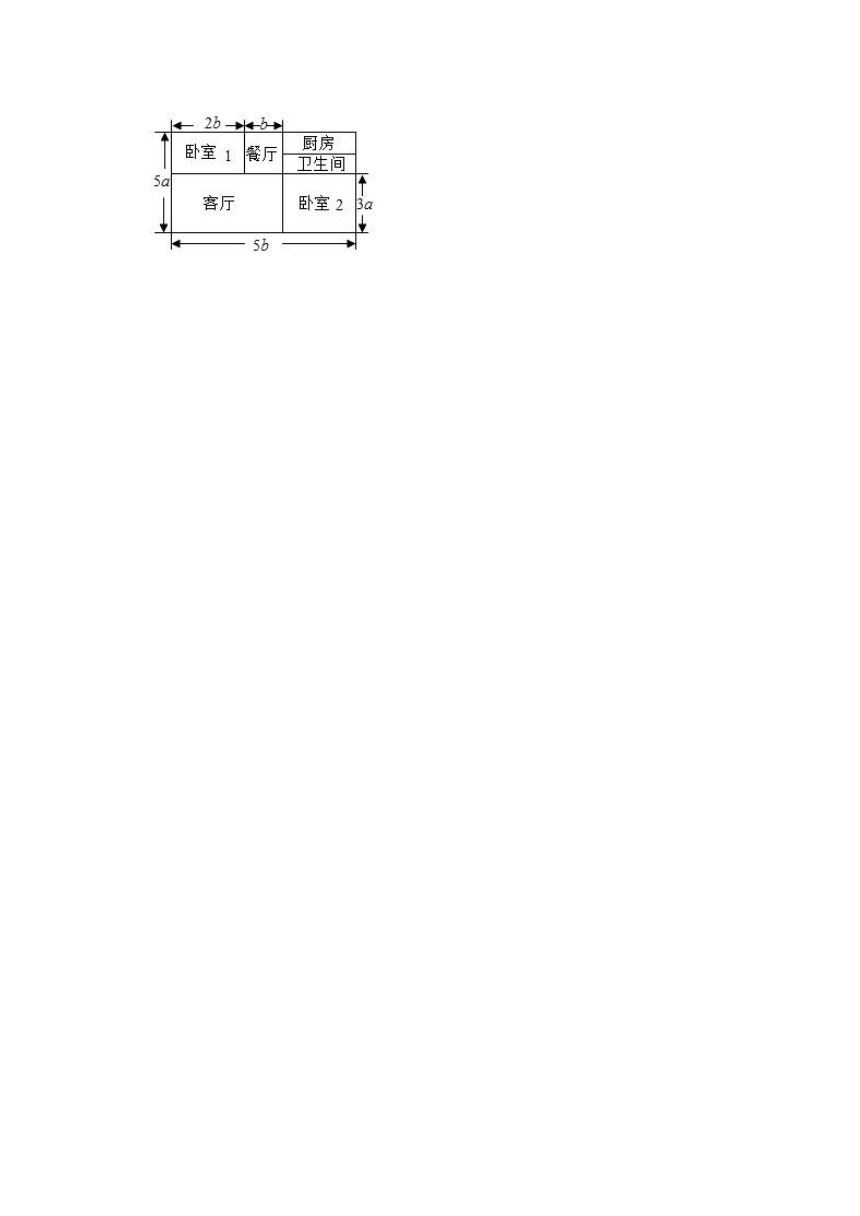
26.(8分)小王家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.
(1)木地板和地砖分别需要多少平方米?
(2)如果地砖的价格为每平方米k元,木地板的价格为每平方米2k元,那么小王一共需要花多少钱?
参考答案
一、单项选择题(本大题共有6小题,每题2分,共12分)
1.(2分)下列不能表示“2a”的意义的是( )
A.2的a倍 B.a的2倍 C.2个a相加 D.2个a相乘
解:2个a相乘表示为a2,
故选:D.
2.(2分)下列式子中,单项式是( )
A.3a+1 B. C.3a D.x=1
解:A、3a+1是多项式,故此选项不合题意;
B、是分式,故此选项不合题意;
C、3a是单项式,符合题意;
D、x=1是方程,故此选项不合题意.
故选:C.
3.(2分)下列各选项中是同类项的是( )
A.﹣a2b和ab2 B.a2和22
C.﹣ab2和2b2a D.2ab和2xy
解:A.﹣a2b和ab2相同字母的指数不相同,不是同类项;
B.a2和22所含字母不相同,不是同类项;
C.﹣ab2和2b2a所含字母相同,且相同字母的指数也相同,是同类项;
D.2ab与2xy所含字母不相同,不是同类项;
故选:C.
4.(2分)下列运算正确( )
A.a2+a3=a5 B.a2?a3=a6
C.(a2)3=a8 D.(﹣a)2?a3=a5
解:A.a2和a3不能合并,故本选项不符合题意;
B.结果是a5,故本选项不符合题意;
C.结果是a6,故本选项不符合题意;
D.结果是a5,故本选项符合题意;
故选:D.
5.(2分)如果M=x2+6x+22,N=﹣x2+6x﹣3,那么M与N的大小关系是( )
A.M>N B.M<N C.M=N D.无法确定
解:∵M=x2+6x+22,N=﹣x2+6x﹣3,
∴M﹣N=x2+6x+22﹣(﹣x2+6x﹣3)
=x2+6x+22+x2﹣6x+3
=2x2+25,
∵x2≥0,
∴2x2+25>0,
∴M>N.
故选:A.
6.(2分)按下面的程序计算,如果输入x的值是30,那么输出的结果为( )
A.470 B.471 C.118 D.119
解:当x=30时,4x﹣2=4×30﹣2=118,
∵118<149,
∴继续代入运算得:4×118﹣2=470,
故选:A.
二、填空题(本大题共有12小题,每题3分,共36分)
7.(3分)单项式的次数是 3 .
解:单项式的次数是:3.
故答案为:3.
8.(3分)x、y两数的平方和减去它们的积的2倍,用代数式表示为 x2+y2﹣2xy .
解:x2+y2﹣2xy.
故答案为:x2+y2﹣2xy.
9.(3分)计算:x2?x3?x4= x9 .
解:原式=x2+3+4
=x9.
故答案为:x9.
10.(3分)计算:(x2)5= x10 .
解:(x2)5=x2×5=x10.
故答案为:x10.
11.(3分)比较大小:25 < 43(填>,<或=).
解:∵43=(22)3=26,25<26,
∴25<43,
故答案为<.
12.(3分)化简3a﹣[a﹣2(a﹣b)]+b,结果是 4a﹣b .
解:原式=3a﹣(a﹣2a+2b)+b
=3a﹣a+2a﹣2b+b
=4a﹣b,
故答案为:4a﹣b
13.(3分)当1<a<2时,代数式|a﹣2|+|1﹣a|的值是 1 .
解:∵1<a<2,
∴a﹣2<0,1﹣a<0,
则原式=2﹣a+a﹣1=1,
故答案为:1
14.(3分)若a与b互为相反数,m和n互为倒数,则= .
解:∵a与b互为相反数,
∴a+b=0,
∵m和n互为倒数,
∴mn=1,
∴(a+b)+mn=×0+×1=,
故答案为:.
15.(3分)已知单项式﹣anb3与单项式﹣2a2bm﹣2是同类项,则m﹣n= 3 .
解:∵单项式﹣anb3与单项式﹣2a2bm﹣2是同类项,
∴n=2,m﹣2=3,
解得:m=5,
∴m﹣n=5﹣2=3,
故答案为:3.
16.(3分)若9×32m×33m=322,则m的值为 4 .
解:∵9×32m×33m=32×32m×33m=32+2m+3m=32+5m=322,
∴2+5m=22,
解得m=4.
故答案为:4.
17.(3分)如果两个关于x的多项式4x2﹣bx﹣5+c与ax2+2x﹣3相等,则a+bc= 0 .
解:∵关于x的多项式4x2﹣bx﹣5+c与ax2+2x﹣3相等,
∴a=4,﹣b=2,﹣5+c=﹣3,
解得b=﹣2,c=2,
∴a+bc=4﹣2×2=0.
故答案为:0.
18.(3分)如图,四张大小不一的四方形纸片分别放置于矩形的四个角落,其中①和②纸片既不重叠也无空隙.已知矩形ABCD的周长为a,阴影部分的周长为b那么以下四个正方形中 ② 号正方形的边长可以直接用a、b表示,结果为 .
解:根据题意得:
阴影部分所有竖直的边长之和=AB+CD,
所有水平的边长之和=(AD﹣②的边长)+(BC﹣②的边长),
则阴影部分的周长=(AB+CD+BC+AD)﹣②的边长×2,
=矩形ABCD的周长﹣②的边长×2,
∵矩形ABCD的周长为a,阴影部分的周长为b,
∴b=a﹣②的边长×2,
∴②的边长=,
故答案为:.
三、解答题(本大题共8小题,第19至24题每题6分,第25、26题每题8分,共52分)
19.(6分)计算:9m2﹣4(2m2﹣3mn+n2)+4n2.
解:原式=9m2﹣8m2+12mn﹣4n2+4n2
=m2+12mn.
20.(6分)计算:x2?x3+(﹣x)5+(x2)3.
解:x2?x3+(﹣x)5+(x2)3
=x5﹣x5+x6
=x6.
21.(6分)(a﹣b)2?(b﹣a)3?(b﹣a)(结果用幂的形式表示)
解:(a﹣b)2?(b﹣a)3?(b﹣a)
=(b﹣a)2?(b﹣a)3?(b﹣a)
=(b﹣a)2+3+1
=(b﹣a)6.
22.(6分)已知多项式.
(1)把这个多项式按x的降幂重新排列;
(2)请指出该多项式的次数,并写出它的二次项和常数项.
解:(1)按x降幂排列为:;
(2)该多项式的次数是5,
它的二次项是xy,常数项是.
23.(6分)已知:m2+mn=30,mn﹣n2=﹣10,求下列代数式的值:
(1)m2+2mn﹣n2;
(2)m2+n2﹣7.
解:(1)∵m2+mn=30,mn﹣n2=﹣10,
∴m2+2mn﹣n2
=(m2+mn)+(mn﹣n2)
=30+(﹣10)
=20
(2)∵m2+mn=30,mn﹣n2=﹣10,
∴m2+n2﹣7
=(m2+mn)﹣(mn﹣n2)﹣7
=30﹣(﹣10)﹣7
=33
24.(6分)化简求值,其中x=2,y=﹣0.5.
解:原式=4x﹣6y﹣2﹣3x﹣2y+2
=x﹣8y,
当x=2,y=﹣0.5时,原式=2+4=6.
25.(8分)已知(x3)n+1=(xn﹣1)4?(x3)2,求(﹣n2)3的值.
解:∵x3n+3=x4n﹣4?x6,
∴3n+3=4n﹣4+6,
解得n=1,
∴(﹣n2)3=(﹣12)3=﹣1.
26.(8分)小王家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.
(1)木地板和地砖分别需要多少平方米?
(2)如果地砖的价格为每平方米k元,木地板的价格为每平方米2k元,那么小王一共需要花多少钱?
解:(1)木地板的面积为2b(5a﹣3a)+3a(5b﹣2b﹣b)
=2b?2a+3a?2b
=4ab+6ab
=10ab(平方米);
地砖的面积为5a?5b﹣10ab=25ab﹣10ab=15ab(平方米);
(2)15ab?k+10ab?2k
=15abk+20abk
=35abk(元),
答:小王一共需要花35abk元钱.
一、选择题(共6小题).
1.(2分)下列不能表示“2a”的意义的是( )
A.2的a倍 B.a的2倍 C.2个a相加 D.2个a相乘
2.(2分)下列式子中,单项式是( )
A.3a+1 B. C.3a D.x=1
3.(2分)下列各选项中是同类项的是( )
A.﹣a2b和ab2 B.a2和22
C.﹣ab2和2b2a D.2ab和2xy
4.(2分)下列运算正确( )
A.a2+a3=a5 B.a2?a3=a6
C.(a2)3=a8 D.(﹣a)2?a3=a5
5.(2分)如果M=x2+6x+22,N=﹣x2+6x﹣3,那么M与N的大小关系是( )
A.M>N B.M<N C.M=N D.无法确定
6.(2分)按下面的程序计算,如果输入x的值是30,那么输出的结果为( )
A.470 B.471 C.118 D.119
二、填空题(共12小题).
7.(3分)单项式的次数是 .
8.(3分)x、y两数的平方和减去它们的积的2倍,用代数式表示为 .
9.(3分)计算:x2?x3?x4= .
10.(3分)计算:(x2)5= .
11.(3分)比较大小:25 43(填>,<或=).
12.(3分)化简3a﹣[a﹣2(a﹣b)]+b,结果是 .
13.(3分)当1<a<2时,代数式|a﹣2|+|1﹣a|的值是 .
14.(3分)若a与b互为相反数,m和n互为倒数,则= .
15.(3分)已知单项式﹣anb3与单项式﹣2a2bm﹣2是同类项,则m﹣n= .
16.(3分)若9×32m×33m=322,则m的值为 .
17.(3分)如果两个关于x的多项式4x2﹣bx﹣5+c与ax2+2x﹣3相等,则a+bc= .
18.(3分)如图,四张大小不一的四方形纸片分别放置于矩形的四个角落,其中①和②纸片既不重叠也无空隙.已知矩形ABCD的周长为a,阴影部分的周长为b那么以下四个正方形中 号正方形的边长可以直接用a、b表示,结果为 .
三、解答题(本大题共8小题,第19至24题每题6分,第25、26题每题8分,共52分)
19.(6分)计算:9m2﹣4(2m2﹣3mn+n2)+4n2.
20.(6分)计算:x2?x3+(﹣x)5+(x2)3.
21.(6分)(a﹣b)2?(b﹣a)3?(b﹣a)(结果用幂的形式表示)
22.(6分)已知多项式.
(1)把这个多项式按x的降幂重新排列;
(2)请指出该多项式的次数,并写出它的二次项和常数项.
23.(6分)已知:m2+mn=30,mn﹣n2=﹣10,求下列代数式的值:
(1)m2+2mn﹣n2;
(2)m2+n2﹣7.
24.(6分)化简求值,其中x=2,y=﹣0.5.
25.(8分)已知(x3)n+1=(xn﹣1)4?(x3)2,求(﹣n2)3的值.
26.(8分)小王家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.
(1)木地板和地砖分别需要多少平方米?
(2)如果地砖的价格为每平方米k元,木地板的价格为每平方米2k元,那么小王一共需要花多少钱?
参考答案
一、单项选择题(本大题共有6小题,每题2分,共12分)
1.(2分)下列不能表示“2a”的意义的是( )
A.2的a倍 B.a的2倍 C.2个a相加 D.2个a相乘
解:2个a相乘表示为a2,
故选:D.
2.(2分)下列式子中,单项式是( )
A.3a+1 B. C.3a D.x=1
解:A、3a+1是多项式,故此选项不合题意;
B、是分式,故此选项不合题意;
C、3a是单项式,符合题意;
D、x=1是方程,故此选项不合题意.
故选:C.
3.(2分)下列各选项中是同类项的是( )
A.﹣a2b和ab2 B.a2和22
C.﹣ab2和2b2a D.2ab和2xy
解:A.﹣a2b和ab2相同字母的指数不相同,不是同类项;
B.a2和22所含字母不相同,不是同类项;
C.﹣ab2和2b2a所含字母相同,且相同字母的指数也相同,是同类项;
D.2ab与2xy所含字母不相同,不是同类项;
故选:C.
4.(2分)下列运算正确( )
A.a2+a3=a5 B.a2?a3=a6
C.(a2)3=a8 D.(﹣a)2?a3=a5
解:A.a2和a3不能合并,故本选项不符合题意;
B.结果是a5,故本选项不符合题意;
C.结果是a6,故本选项不符合题意;
D.结果是a5,故本选项符合题意;
故选:D.
5.(2分)如果M=x2+6x+22,N=﹣x2+6x﹣3,那么M与N的大小关系是( )
A.M>N B.M<N C.M=N D.无法确定
解:∵M=x2+6x+22,N=﹣x2+6x﹣3,
∴M﹣N=x2+6x+22﹣(﹣x2+6x﹣3)
=x2+6x+22+x2﹣6x+3
=2x2+25,
∵x2≥0,
∴2x2+25>0,
∴M>N.
故选:A.
6.(2分)按下面的程序计算,如果输入x的值是30,那么输出的结果为( )
A.470 B.471 C.118 D.119
解:当x=30时,4x﹣2=4×30﹣2=118,
∵118<149,
∴继续代入运算得:4×118﹣2=470,
故选:A.
二、填空题(本大题共有12小题,每题3分,共36分)
7.(3分)单项式的次数是 3 .
解:单项式的次数是:3.
故答案为:3.
8.(3分)x、y两数的平方和减去它们的积的2倍,用代数式表示为 x2+y2﹣2xy .
解:x2+y2﹣2xy.
故答案为:x2+y2﹣2xy.
9.(3分)计算:x2?x3?x4= x9 .
解:原式=x2+3+4
=x9.
故答案为:x9.
10.(3分)计算:(x2)5= x10 .
解:(x2)5=x2×5=x10.
故答案为:x10.
11.(3分)比较大小:25 < 43(填>,<或=).
解:∵43=(22)3=26,25<26,
∴25<43,
故答案为<.
12.(3分)化简3a﹣[a﹣2(a﹣b)]+b,结果是 4a﹣b .
解:原式=3a﹣(a﹣2a+2b)+b
=3a﹣a+2a﹣2b+b
=4a﹣b,
故答案为:4a﹣b
13.(3分)当1<a<2时,代数式|a﹣2|+|1﹣a|的值是 1 .
解:∵1<a<2,
∴a﹣2<0,1﹣a<0,
则原式=2﹣a+a﹣1=1,
故答案为:1
14.(3分)若a与b互为相反数,m和n互为倒数,则= .
解:∵a与b互为相反数,
∴a+b=0,
∵m和n互为倒数,
∴mn=1,
∴(a+b)+mn=×0+×1=,
故答案为:.
15.(3分)已知单项式﹣anb3与单项式﹣2a2bm﹣2是同类项,则m﹣n= 3 .
解:∵单项式﹣anb3与单项式﹣2a2bm﹣2是同类项,
∴n=2,m﹣2=3,
解得:m=5,
∴m﹣n=5﹣2=3,
故答案为:3.
16.(3分)若9×32m×33m=322,则m的值为 4 .
解:∵9×32m×33m=32×32m×33m=32+2m+3m=32+5m=322,
∴2+5m=22,
解得m=4.
故答案为:4.
17.(3分)如果两个关于x的多项式4x2﹣bx﹣5+c与ax2+2x﹣3相等,则a+bc= 0 .
解:∵关于x的多项式4x2﹣bx﹣5+c与ax2+2x﹣3相等,
∴a=4,﹣b=2,﹣5+c=﹣3,
解得b=﹣2,c=2,
∴a+bc=4﹣2×2=0.
故答案为:0.
18.(3分)如图,四张大小不一的四方形纸片分别放置于矩形的四个角落,其中①和②纸片既不重叠也无空隙.已知矩形ABCD的周长为a,阴影部分的周长为b那么以下四个正方形中 ② 号正方形的边长可以直接用a、b表示,结果为 .
解:根据题意得:
阴影部分所有竖直的边长之和=AB+CD,
所有水平的边长之和=(AD﹣②的边长)+(BC﹣②的边长),
则阴影部分的周长=(AB+CD+BC+AD)﹣②的边长×2,
=矩形ABCD的周长﹣②的边长×2,
∵矩形ABCD的周长为a,阴影部分的周长为b,
∴b=a﹣②的边长×2,
∴②的边长=,
故答案为:.
三、解答题(本大题共8小题,第19至24题每题6分,第25、26题每题8分,共52分)
19.(6分)计算:9m2﹣4(2m2﹣3mn+n2)+4n2.
解:原式=9m2﹣8m2+12mn﹣4n2+4n2
=m2+12mn.
20.(6分)计算:x2?x3+(﹣x)5+(x2)3.
解:x2?x3+(﹣x)5+(x2)3
=x5﹣x5+x6
=x6.
21.(6分)(a﹣b)2?(b﹣a)3?(b﹣a)(结果用幂的形式表示)
解:(a﹣b)2?(b﹣a)3?(b﹣a)
=(b﹣a)2?(b﹣a)3?(b﹣a)
=(b﹣a)2+3+1
=(b﹣a)6.
22.(6分)已知多项式.
(1)把这个多项式按x的降幂重新排列;
(2)请指出该多项式的次数,并写出它的二次项和常数项.
解:(1)按x降幂排列为:;
(2)该多项式的次数是5,
它的二次项是xy,常数项是.
23.(6分)已知:m2+mn=30,mn﹣n2=﹣10,求下列代数式的值:
(1)m2+2mn﹣n2;
(2)m2+n2﹣7.
解:(1)∵m2+mn=30,mn﹣n2=﹣10,
∴m2+2mn﹣n2
=(m2+mn)+(mn﹣n2)
=30+(﹣10)
=20
(2)∵m2+mn=30,mn﹣n2=﹣10,
∴m2+n2﹣7
=(m2+mn)﹣(mn﹣n2)﹣7
=30﹣(﹣10)﹣7
=33
24.(6分)化简求值,其中x=2,y=﹣0.5.
解:原式=4x﹣6y﹣2﹣3x﹣2y+2
=x﹣8y,
当x=2,y=﹣0.5时,原式=2+4=6.
25.(8分)已知(x3)n+1=(xn﹣1)4?(x3)2,求(﹣n2)3的值.
解:∵x3n+3=x4n﹣4?x6,
∴3n+3=4n﹣4+6,
解得n=1,
∴(﹣n2)3=(﹣12)3=﹣1.
26.(8分)小王家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.
(1)木地板和地砖分别需要多少平方米?
(2)如果地砖的价格为每平方米k元,木地板的价格为每平方米2k元,那么小王一共需要花多少钱?
解:(1)木地板的面积为2b(5a﹣3a)+3a(5b﹣2b﹣b)
=2b?2a+3a?2b
=4ab+6ab
=10ab(平方米);
地砖的面积为5a?5b﹣10ab=25ab﹣10ab=15ab(平方米);
(2)15ab?k+10ab?2k
=15abk+20abk
=35abk(元),
答:小王一共需要花35abk元钱.
同课章节目录
